Statistika Deskriptif Statistika Deskriptif Parameter Populasi 1 Bab

Statistika Deskriptif �Statistika Deskriptif: �Parameter Populasi 1

Bab 3 A STATISTIKA DESKRIPTIF: PARAMETER POPULASI 1 A. Parameter Rerata 1. Batasan dan Jenis � Skala data paling rendah adalah pada level interval (interval dan rasio) � Ada tiga jenis rerata mencakup Rerata hitung (sering disebut rerata saja) Rerata ukur Rerata harmonik

2. Parameter Rerata Hitung (a) Rumus rerata hitung � Dengan N sebagai banyaknya data, rerata untuk data X dan Y adalah


Cara lain menghitung rerata X 7 7 6 5 4 4 4 3 40 Y 10 9 9 6 5 4 3 2 1 1 50 X = 40 / 8 = 5 Y = 50 / 10 = 5 Cara ini lebih praktis daripada cara pertama sehingga digunakan secara umum

(b) Rumus dengan Frekuensi Rumus rerata dengan melibatkan frekuensi Rumus ini lebih praktis untuk data dengan berbagai frekuensi

---------------------------------------Bab 3 A --------------------------------------- Contoh 2 X Y 7 10 7 9 6 9 5 6 4 5 4 4 4 3 3 2 1 1 X 7 6 5 4 3 f 2 1 1 3 1 8 Y 10 9 6 5 4 3 2 1 f. X 14 6 5 12 3 40 f. Y 10 2 18 1 6 1 5 1 4 1 3 1 2 2 2 10 50 X = 40 / 8 = 5 Y = 50 / 10 = 5
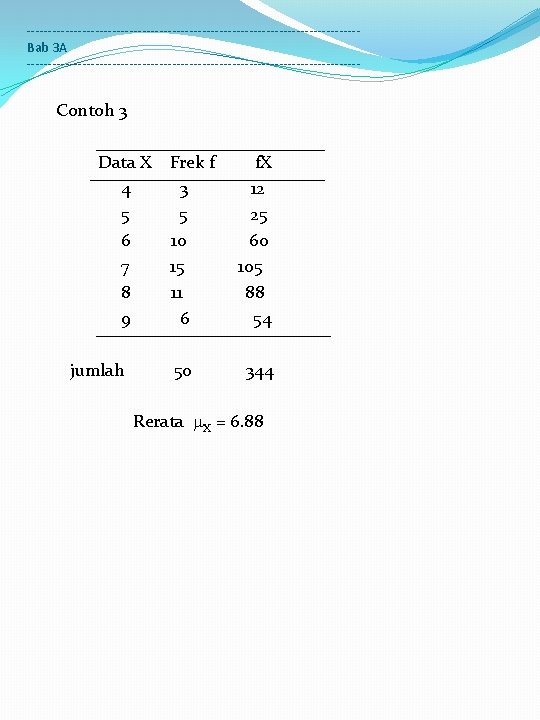
---------------------------------------Bab 3 A --------------------------------------- Contoh 3 Data X 4 5 6 7 8 9 jumlah Frek f 3 5 10 15 11 6 50 f. X 12 25 60 105 88 54 344 Rerata X = 6. 88

Contoh 4 Data Y 0 1 2 3 4 5 6 7 8 9 10 Frek f 0 1 0 5 9 15 23 15 17 9 6 Rerata Y = f. Y 0 1

Contoh 5 Kelompok 31 – 40 41 – 50 51 – 60 61 – 70 71 – 80 81 – 90 91 – 100 Nilai kel X 35, 5 45, 5 55, 5 65, 5 75, 5 85, 5 95, 5 Rerata X = Frek f f. X 2 71 3 91 5 14 25 18 13

(c) Perhitungan dengan Kalkulator Elektronik Cara pakai kalkulator elektronik tercantum di dalam manual kalkulator itu Sebagai contoh di sini digunakan Casio fx 350 TL Contoh 6 X : 7 7 6 5 4 4 4 3 Mode 2 (ke statistika rerata) Shift AC = AC (membersihkan isi memori) 7 shift ; 2 DT (frekuensi 2) 6 DT 5 DT 4 shift ; 3 DT (frekuensi 3) 3 DT Shift X = (tampilkan rerata 5) Mode 1 (kembali ke kalkulator biasa)

Contoh 7 Dengan kalkulator elektronik, hitung kembali rerata pada Contoh 2, 3, 4, dan 5 Contoh 8 Dengan Excel/kalkulator elektronik, hitung rerata dari 79 80 70 68 90 92 80 70 63 76 49 48 74 84 90 70 71 92 38 72 85 53 32 83 73 93 76 71 91 61 72 74 99 95 60 83 82 63 88 70 = 81 91 56 65 74 90 97 80 60 66 98 93 91 93 43 72 91 59 67 80 87 82 74 83 86 67 88 71 89 79 80 78 73 86 68 75 81 77 63 75
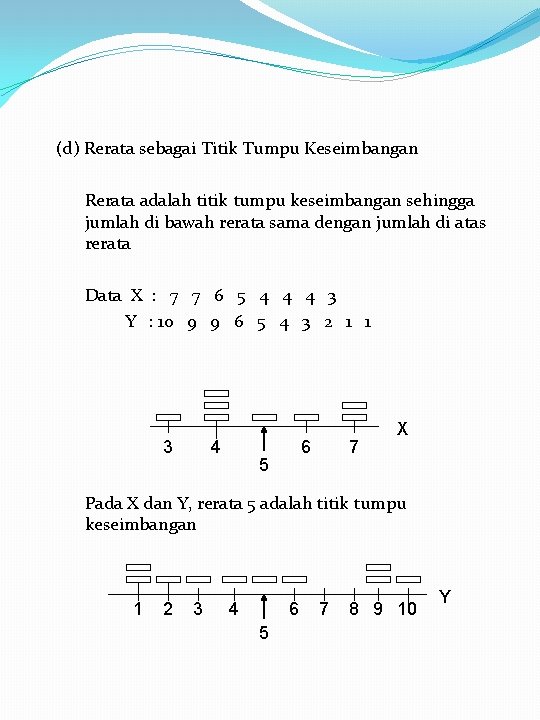
(d) Rerata sebagai Titik Tumpu Keseimbangan Rerata adalah titik tumpu keseimbangan sehingga jumlah di bawah rerata sama dengan jumlah di atas rerata Data X : 7 7 6 5 4 4 4 3 Y : 10 9 9 6 5 4 3 2 1 1 3 4 6 5 7 X Pada X dan Y, rerata 5 adalah titik tumpu keseimbangan 1 2 3 4 6 5 7 8 9 10 Y

3. Parameter Rerata Hitung pada Data Dikotomi Khusus pada data dikotomi, rerata sama dengan proporsi X = sehingga pada umumnya, digunakan proporsi Contoh 9 Data X 1 0 1 0 1 1 1 7 X = 7 / 10 = 0, 7 X = 7 dari 10 = 0, 7 X = 0, 7

4. Parameter Rerata Ukur Rerata ukur adalah perkalian data yang ditarik akarnya sebesar banyaknya data Rumus rerata ukur Contoh 10 Data : 3 4 5 Rerata ukur Data : 2 2 4 5 7 8 8 Rarata ukur U=
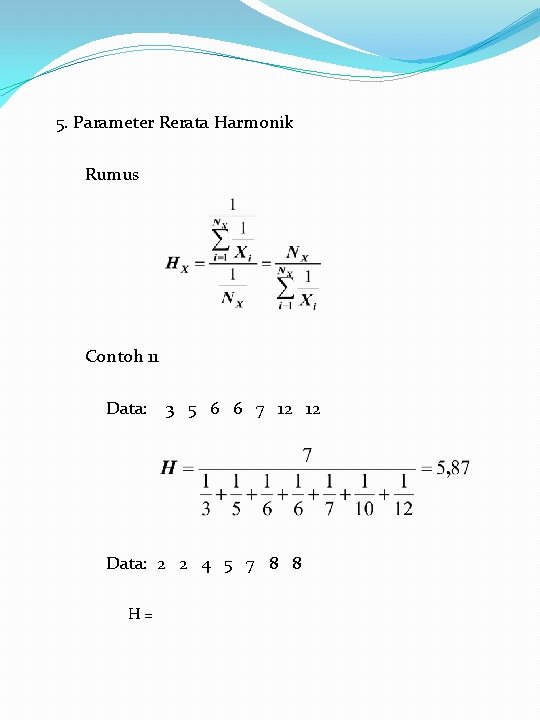
5. Parameter Rerata Harmonik Rumus Contoh 11 Data: 3 5 6 6 7 12 12 Data: 2 2 4 5 7 8 8 H=
6. Kecondongan (skewness) Kecondongan distribusi Distribusi frekuensi atau distribusi proporsi dapat saja • • • Simetri Condong ke kiri atau positif Condong ke kanan atau negatif Distribusi simetri modus = median = rerata (hitung)
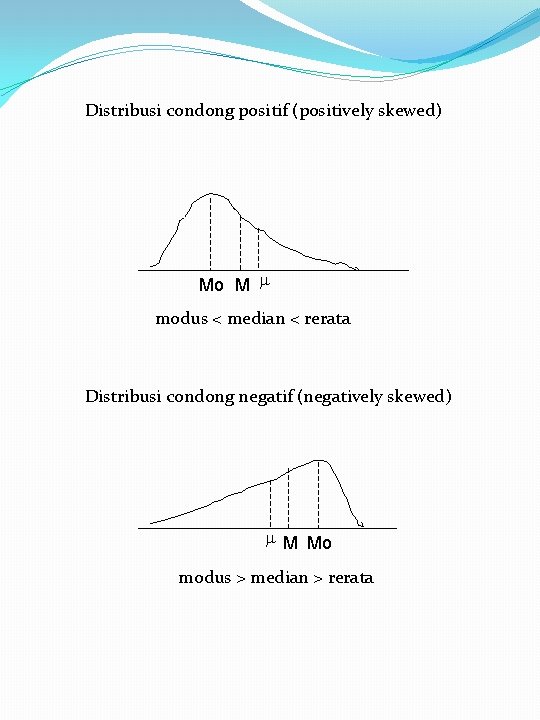
Distribusi condong positif (positively skewed) Mo M modus < median < rerata Distribusi condong negatif (negatively skewed) M Mo modus > median > rerata

7. Kurtosis (kepuncakan) Kurtosis distribusi Distribusi frekuensi atau distribusi proporsi dapat saja memiliki puncak • • • Mesokurtik (puncak biasa) Leptokurtik (puncak tinggi) Platikurtik (puncak rendah) Mesokurtik

Leptokurtik (puncak tinggi) Platikurtik (puncak rencah)

B. Parameter Variansi dan Simpangan Baku 1. Penyebaran Data � Penyebaran data ini diacu kepada rerata hitung yakni berapa lebar data itu menyebar di sekitar rerata hitung � Penyebaran data ini mencakup beberapa parameter Simpangan Jumlah Kuadrat Simpangan Variansi Simpangan Baku � Selain rerata hitung, parameter variansi dan simpangan baku merupakan parameter yang banyak digunakan di dalam statistika

2. Simpangan (a) Nilai simpangan = nilai data – rerata hitung x = X – X y = Y – Y � Nilai di atas rerata memperoleh simpangan positif � Nilai sama dengan rerata memperoleh simpangan nol � Nilai di bawah rerata memperoleh simpangan negatif
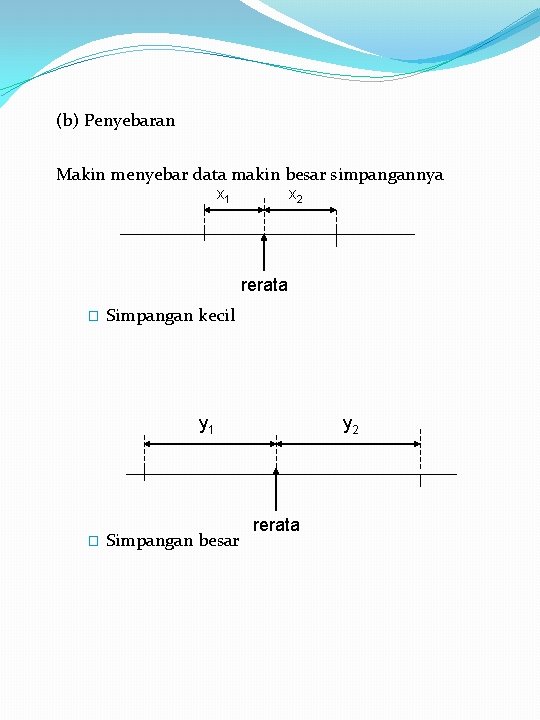
(b) Penyebaran Makin menyebar data makin besar simpangannya x 1 x 2 rerata � Simpangan kecil y 1 � Simpangan besar y 2 rerata

Contoh 12 Data X Simpangan x 7 2 6 1 5 0 4 – 1 3 – 2 0 Data Y 10 9 9 6 5 4 3 2 1 1 X = 5 (c) Jumlah Simpangan y 5 4 4 1 0 – 1 – 2 – 3 – 4 0 Y = 5 Karena rerata adalah titik tumpu keseimbangan maka jumlah simpangan (negatif dan positf) adalah nol x=0 y=0
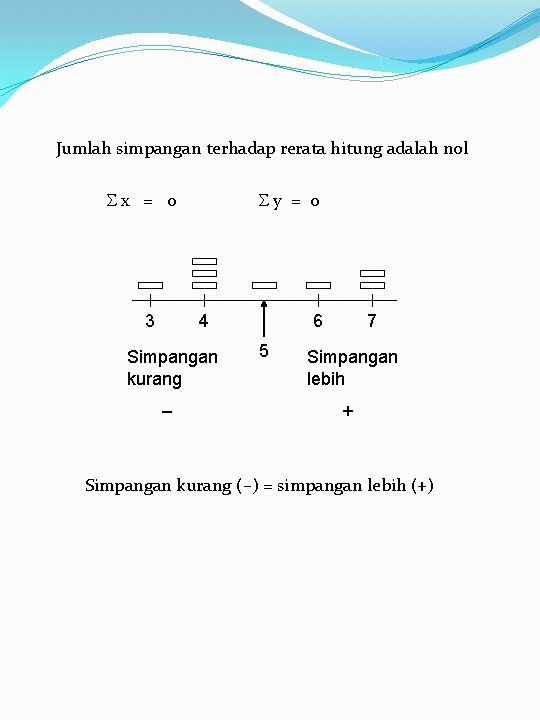
Jumlah simpangan terhadap rerata hitung adalah nol x = 0 3 y = 0 4 Simpangan kurang – 6 5 7 Simpangan lebih + Simpangan kurang (–) = simpangan lebih (+)

Contoh 13 Data X Frek f 4 3 5 5 6 10 7 15 8 11 9 6 X = f. X 12 25 Simp x – 2, 88 f. Y Simp y Contoh 14 Data Y Frek f 1 1 3 5 4 9 5 15 6 23 7 15 8 17 9 9 10 6 Y =

3. Jumlah Kuadrat Simpangan (a) Hakikat � Sering disingkat sebagai jumlah kuadrat JK � Karena simpangan bernilai negatif dan positif dan jumlah mereka adalah nol, maka sebelum dijumlahkan simpangan dikuadratkan � Jumlah dari simpangan yang dikuadratkan ini merupakan jumlah kuadrat � Makin besar simpangan, makin besar jumlah kuadrat sehingga JK merupakan indikator dari penyebaran data � Makin lebar penyebaran data makin besar nilai jumlah kuadrat (JK)

(b) Rumus Jumlah Kuadrat Simpangan JK = x 2 = (X – X)2 Melalui aljabar, JK dapat juga dinyatakan melalui dengan NX sebagai banyaknya data Contoh 15 Data X X 2 7 49 6 36 5 25 4 16 3 9 40 216 JK = 216 – (40)2 / 8 = 16

4. Parameter Variansi (a) Data Umum • JK bergantung kepada banyaknya data NX sehingga JK dapat berbeda karena banyaknya data berbeda • Untuk mengatasinya, JK dibagi dengan banyaknya data, dan hasil bagi ini dikenal sebagai variansi • Variansi diberi notasi 2 (merupakan ukuran penyebaran data)

Contoh 16 Dari contoh 15, telah diperoleh JK = 16 NX = 8 Variansi 2 X = 16 / 8 = 2 Contoh 17 Data Y Y 2 10 100 9 81 6 36 5 25 4 16 3 9 2 4 1 1 50 354 2 y = 10, 4

Cara hitung menggunakan frekuensi Data Y 10 9 6 5 4 3 2 1 Frek f Y 2 f. Y 1 100 10 2 81 18 1 36 6 1 25 5 1 16 4 1 9 3 1 4 2 2 1 2 50 σ2 Y = 10, 4 f. Y 2 100 162 36 25 16 9 4 2 354

(b) Data Dikotomi Pada data dikotomi (0 dan 1), rumus variansi dapat disederhanakan menjadi 2 X = (1 – ) Dalam hal data dikotomi, terdapat nilai maksimum pada variansi 2 X maks = 0, 25 pada = 0, 5 Contoh 18 X Y 1 1 0 0 1 1 0 1 2 X = (0, 4)(1 – 0, 4) = 0, 24 2 Y = (0, 8)(1 – 0, 8) = 0, 16

5. Parameter Simpangan Baku (a) Hakikat Simpangan Baku • Simpangan baku adalah akar dua positif dari variansi • Simpangan baku merupakan simpangan yang dibakukan • Simpangan baku bersama-sama dengan variansi merupakan ukuran penyebaran data • Simpangan baku sering dijadikan satuan dari simpangan data • Simpangan baku diberi notasi

Simpangan, jumlah kuadrat, variansi, dan simpangan baku menunjukkan penyebaran data Makin lebar penyebaran data, maka besar nilai mereka � � � � � Penyebaran Nilai simpangan Jumlah kuadrat Variansi Simpangan baku : kecil : kecil Penyebaran Nilai simpangan Jumlah kuadrat Variansi Simpangan baku : besar : besar

Contoh 19 Dari contoh 16 X = √ 2 = 1, 41 Dari contoh 17 Y = √ 10, 40 = 3, 22 Dari contoh 18 X = √ 0, 24 = 0, 44 Y = √ 0, 16 = 0, 40

(b) Perhitungan dengan Kalkulator Simpangan baku dapat langsung dihitung dengan bantuan kalkulator elektronik Caranya dapat dibaca pada manual Contoh pada kalkulator Casio fx 350 TL � Langkahnya sama dengan langkah pada perhitungan rerata dengan kalkulator Casio fx 350 TL � Untuk membaca simpangan baku tekan x n = � atau y n = Tekan tombol x 2 untuk menemukan variansi

Contoh 20 Data X 4 5 6 7 8 9 Frek f 3 5 10 15 11 6 50 X 2 16 25 36 49 64 81 f. X 2 12 48 25 125 60 360 105 735 88 704 54 486 344 2458 Variansi 2 X = 2458 - (344)2 /50=91, 28 Simpangan baku X = 9, 55 Hitung kembali dengan menggunakan Exel atau kalkulator elektronik

Contoh 21 Data Y 1 3 4 5 6 7 8 9 10 � Frek f 1 5 9 15 23 15 17 9 6 Hitung Y 2 f. Y 2 2 Y = � Hitung kembali dengan menggunakan kalkulator elektronik

Contoh 22 Kelompok 31 – 40 41 – 50 51 – 60 61 – 70 71 – 80 81 – 90 91 – 100 Nil Kel X Frek f X 2 35, 5 2 3 5 14 25 18 13 Hitung f. X 2 X = Hitung kembali dengan menggunakan Excel/kalkulator elektronik f. X 2

Contoh 23 Data X adalah sebagai berikut 79 80 70 68 90 92 80 70 63 76 49 48 74 84 90 70 71 92 38 72 85 53 32 83 73 93 76 71 91 61 72 74 99 95 60 83 82 63 88 70 81 91 56 65 74 90 97 80 60 66 98 93 91 93 43 72 91 59 67 80 87 82 74 83 86 67 88 71 89 79 80 78 73 86 68 75 81 77 63 75 Dengan kalkulator elektronik, hitung X = 2 X =

Contoh 24 Data Y adalah sebagai berikut 39 29 44 31 46 32 37 26 34 42 22 26 28 21 15 40 25 28 30 33 30 14 38 22 20 29 38 11 32 49 35 26 28 39 33 32 35 21 13 10 26 33 30 23 31 25 43 38 41 37 47 18 30 18 26 37 15 11 11 32 29 26 30 45 21 15 39 33 34 37 14 26 24 19 22 31 20 29 35 41 21 43 28 32 32 Dengan kalkulator elektronik, hitung Y = 2 Y =

Contoh 25 Data X adalah sebagai berikut 161 143 158 166 146 163 156 154 152 145 156 148 147 151 149 157 147 162 157 148 161 154 149 159 160 164 159 156 151 158 163 159 167 152 155 160 153 156 146 154 157 164 149 161 144 152 147 151 156 153 146 165 160 162 149 153 150 155 148 151 159 155 161 162 160 154 149 165 148 160 152 150 161 156 150 155 152 149 158 145 153 156 161 156 154 165 155 148 151 150 162 158 155 157 163 159 152 168 Dengan kalkulator elektronik, hitung X = 2 X =

Contoh 26 1 1 1 1 0 1 1 1 0 1 1 1 0 Data Y 1 1 1 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 1 1 1 0 0 0 0 2 Y Y

C. Nilai Baku dan Transformasi Baku 1. Nilai Baku Linier (a) Hakikat nilai baku � Nilai baku adalah nilai simpangan yang dinyatakan dalam satuan simpangan baku � Nilai baku ini dikenal sebagai nilai baku linier karena ada nilai baku lain yang nonlinier � Nilai baku linier diberi notasi z � Rumus nilai baku (linier)

(b) Sifat Nilai baku Tanda nilai baku adalah relatif terhadap nilai rerata � Nilai baku adalah negatif jika data terletak di bawah rerata � Nilai baku adalah nol jika data terletak tepat pada rerata � Nilai baku adalah positif jika data terletak di atas rerata Nilai dari nilai baku adalah relatif terhadap nilai simpangan baku � Nilai baku menjadi kecil jika simpangan baku adalah besar (sebaran data adalah besar) � Nilai baku menjadi besar jika simpangan baku adalah kecil (sebaran data adalah kecil)
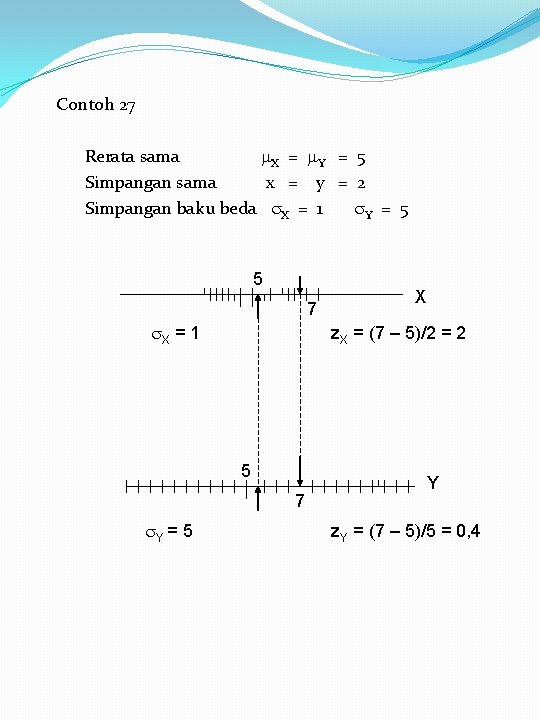
Contoh 27 Rerata sama X = Y = 5 Simpangan sama x = y = 2 Simpangan baku beda X = 1 Y = 5 5 7 X = 1 z. X = (7 – 5)/2 = 2 5 7 Y = 5 X Y z. Y = (7 – 5)/5 = 0, 4

Contoh 28 Data X 7 6 5 4 3 Frek f 2 1 1 3 1 Nilai baku z. X X = Contoh 29 Data Y 10 9 6 5 4 3 2 1 Frek f 1 2 1 1 1 2 Nilai baku z. Y Y =
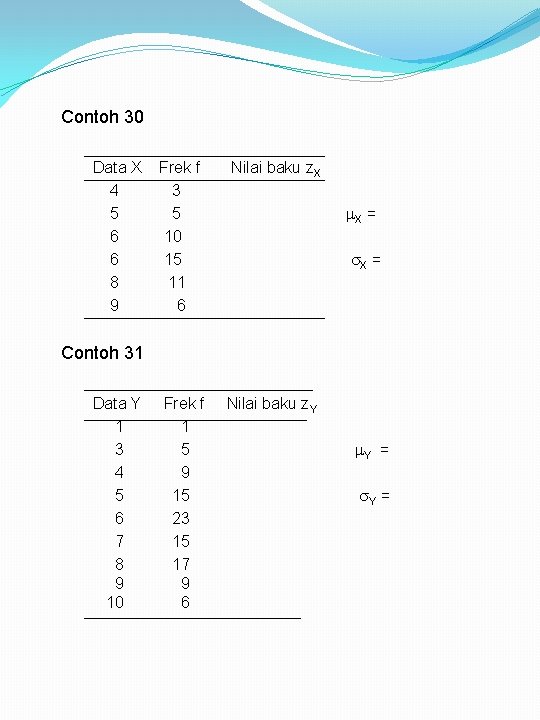
Contoh 30 Data X 4 5 6 6 8 9 Frek f 3 5 10 15 11 6 Nilai baku z. X Frek f 1 5 9 15 23 15 17 9 6 Nilai baku z. Y X = Contoh 31 Data Y 1 3 4 5 6 7 8 9 10 Y =

2. Transformasi Baku Linier (a) Hakikat � Tranformasi baku linier terjadi di antara nilai pada dua sistem (misalnya, X dan Y) � Tranformasi baku ini dikatakan linier karena masih ada transformasi baku lainnya yang nonlinier � Tranformasi baku linier ini dikatakan linier karena apabila nilai diletakkan di sumbu X dan nilai transformasi diletakkan di sumbu Y, maka mereka membentuk garis lurus Y X

(b) Rumus Transformasi Baku Linier Nilai baku setelah tranformasi disamakan dengan nilai baku sebelum transformasi (maka itu dinamakan transformasi baku) Dengan demikian maka
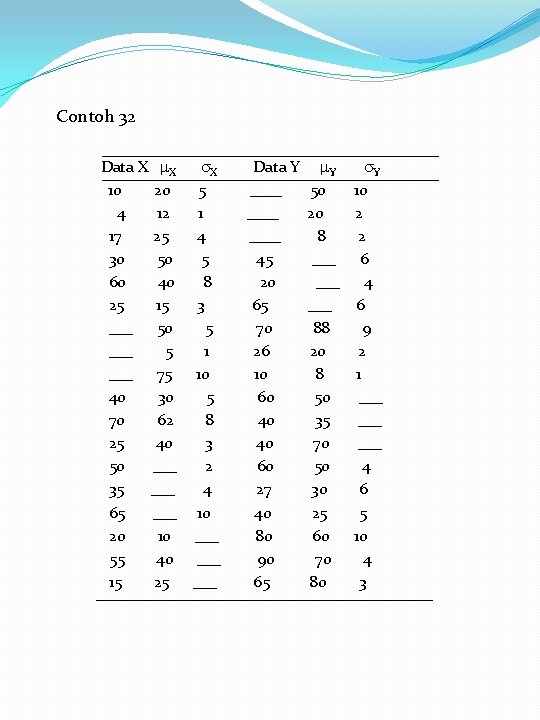
Contoh 32 Data X X 10 20 4 12 17 25 30 50 60 40 25 15 ___ 50 ___ 5 ___ 75 40 30 70 62 25 40 50 ___ 35 ___ 65 ___ 20 10 55 40 15 25 X 5 1 4 5 8 3 5 1 10 5 8 3 2 4 10 ___ ___ Data Y ____ 45 20 65 70 26 10 60 40 40 60 27 40 80 90 65 Y 50 20 8 ___ ___ 88 20 8 50 35 70 50 30 25 60 70 80 Y 10 2 2 6 4 6 9 2 1 ___ ___ 4 6 5 10 4 3

�Bahan U 1: Distribusi frekuensi, Modus, median, rerata, varians dan simpangan baku.
- Slides: 52