STATISTIKA Deret berkala dan Peramalan Julius Nursyamsi Pendahuluan

STATISTIKA Deret berkala dan Peramalan Julius Nursyamsi

Pendahuluan Deret berkala – Time series – Sekumpulan data yang dicatat dalam satu periode waktu – Digunakan untuk meramalkan kondisi masa mendatang – Dalam jangka pendek (kurang dari 1 tahun ) atau jangka panjang (lebih dari 3 tahun) – Berguna untuk penyusunan recana (perusahaan dan negara)

Pendahuluan Deret berkala mempunyai empat komponen : – Tren – kecenderungan – Variasi musim – Variasi siklus – Variasi yang tidak tetap – irregular variation

Tren - Kecenderungan Tren – Merupakan suatu gerakan kecenderungan naik atau turun dalam jangka panjang yang diperoleh dari rata-rata perubahan dari waktu ke waktu dan nilainya cukup rata atau mulus Bentuk tren – Tren positif = tren meningkat Y = a + b. X – Tren negatif = tren menurun Y = a – b. X
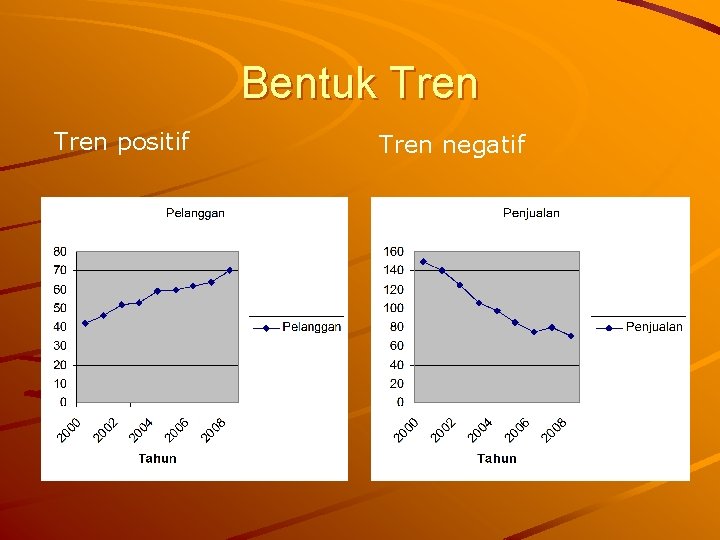
Bentuk Tren positif Tren negatif

Metode Analisa Tren Metode semi rata – rata ( Semi average method) Metode kuadrat terkecil ( Least square method) Metode tren kuadratis ( Quadratic trend method) Metode tren eksponensial ( Exponential trend method)

Metode semi rata - rata Dengan cara mencari rata – rata kelompok data Langkah : – Kelompokan data menjadi dua kelompok – Hitung rata – rata hitung dan letakkan di tengah kelompok ( K 1 dan K 2), menjadi nilai konstanta (a) dan letak tahun merupakan tahun dasar – Hitung selisih K 2 – K 1 K 2 – – K 1 > < 0 0 = = Tren positif negatif

Lanjutam …………. Langkah berikut – Tentukan nilai perubah tern (b) dengan cara : b= K 2 – K 1 th dasar 2 – th dasar 1 – Persamaan tren ; Y’ = a + b. X Untuk mengetahui besarnya tren, masukan nilai (X) pada persamaan – Untuk data ganjil, data (tahun) tengah dapat dihilangkan atau dihitung dua kali
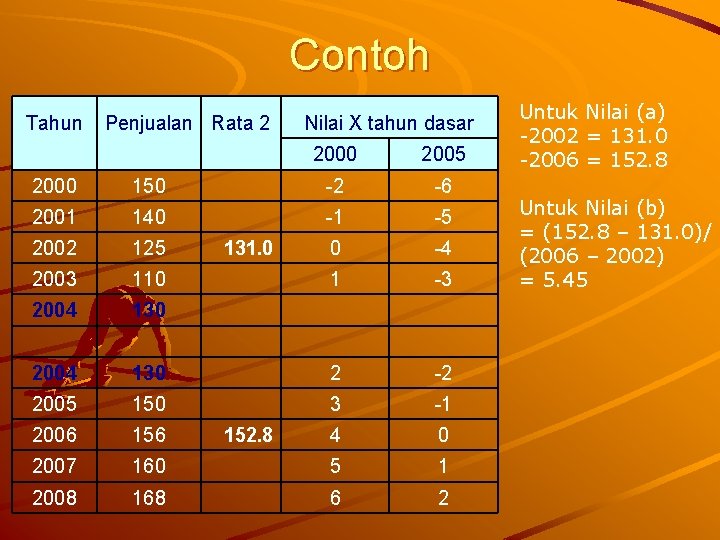
Contoh Tahun Penjualan Rata 2 2000 150 2001 140 2002 125 2003 110 2004 Nilai X tahun dasar 2000 2005 -2 -6 -1 -5 0 -4 1 -3 130 2004 130 2 -2 2005 150 3 -1 2006 156 4 0 2007 160 5 1 2008 168 6 2 131. 0 152. 8 Untuk Nilai (a) -2002 = 131. 0 -2006 = 152. 8 Untuk Nilai (b) = (152. 8 – 131. 0)/ (2006 – 2002) = 5. 45

Lanjutan ……. Maka persamaan tren – Tahun dasar 2002 Y’ = 131+ 5. 45 (X) – Tahun dasar 2006 Y’ = 152. 8 + 5. 45 (X) Peramalan tahun 2009 – Y’ = 131+ 5. 45 (7) – Y’ = 152. 8 + 5. 45 (3) = 169. 15

Metode kuadrat terkecil Dengan menentukan garis tren yang mempunyai jumlah terkecil dari kuadrat selisih data asli dengan data pada garis tren Persamaan ; Y’ = a + b. (X) Mencari nilai koefisien a = (∑ Y ) / n b = (∑XY) / (∑X)2
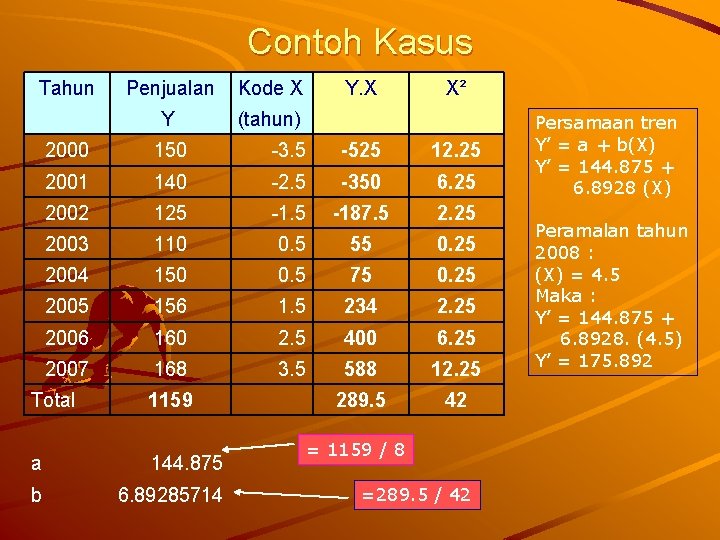
Contoh Kasus Tahun Penjualan Kode X Y. X X² Y (tahun) 2000 150 -3. 5 -525 12. 25 2001 140 -2. 5 -350 6. 25 2002 125 -187. 5 2. 25 2003 110 0. 5 55 0. 25 2004 150 0. 5 75 0. 25 2005 156 1. 5 234 2. 25 2006 160 2. 5 400 6. 25 2007 168 3. 5 588 12. 25 289. 5 42 Total 1159 a 144. 875 b 6. 89285714 = 1159 / 8 =289. 5 / 42 Persamaan tren Y’ = a + b(X) Y’ = 144. 875 + 6. 8928 (X) Peramalan tahun 2008 : (X) = 4. 5 Maka : Y’ = 144. 875 + 6. 8928. (4. 5) Y’ = 175. 892

Metode Tren Kuadratis Digunakan untuk tren jangka panjang yang polanya tidak linier Maka digunakan metode tren kuadratis, persamaan : Y = a + b. X + c. X 2 Nilai koefisien : (∑Y) (∑X 4) – (∑X 2 Y) (∑X 2) Konstanta (a) = n (∑X 4) – (∑X 2)2

Metode Tren Kuadratis Nilai koefisien : Pengubah (b) = ∑XY / ∑X 2 Pengubah (c) = n (∑X 2 Y) - (∑X 2) (∑Y) n (∑X 4) – (∑X 2)2
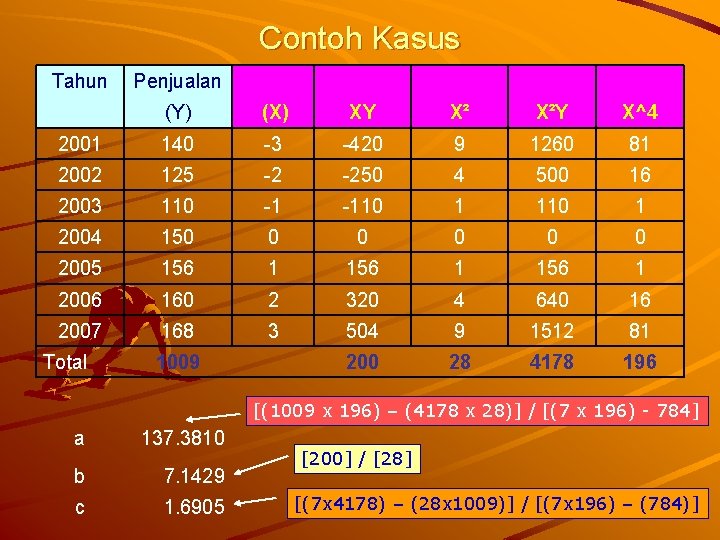
Contoh Kasus Tahun Penjualan (Y) (X) XY X² X²Y X^4 2001 140 -3 -420 9 1260 81 2002 125 -2 -250 4 500 16 2003 110 -1 -110 1 2004 150 0 0 2005 156 1 2006 160 2 320 4 640 16 2007 168 3 504 9 1512 81 1009 200 28 4178 196 Total [(1009 x 196) – (4178 x 28)] / [(7 x 196) - 784] a 137. 3810 b 7. 1429 c 1. 6905 [200] / [28] [(7 x 4178) – (28 x 1009)] / [(7 x 196) – (784)]

Contoh Kasus Persamaan tren kuadratis Y = 137. 3810 + 7. 1429(X) + 1. 6905(X 2) Jadi Peramalan penjualan untuk tahun 2008 (X = 4) adalah : Y = 137. 3810 + 7. 1429(4) + 1. 6905(42) Y = 137. 3810 + 28. 5714 + 27. 0476 Y = 193 Perkiraan penjualan tahun 2009 sebesar 193 unit

Metode tren eksponensial Suatu tren yang mempunyai pangkat atau eksponen dari waktu Bentuk persamaan : Y = a(1 + b)x Koefisien : Konstanta (a) = anti Ln (∑Ln. Y)/n ( Pengubah (b) = anti Ln [(∑X. Ln. Y)/(∑(X)2] - 1
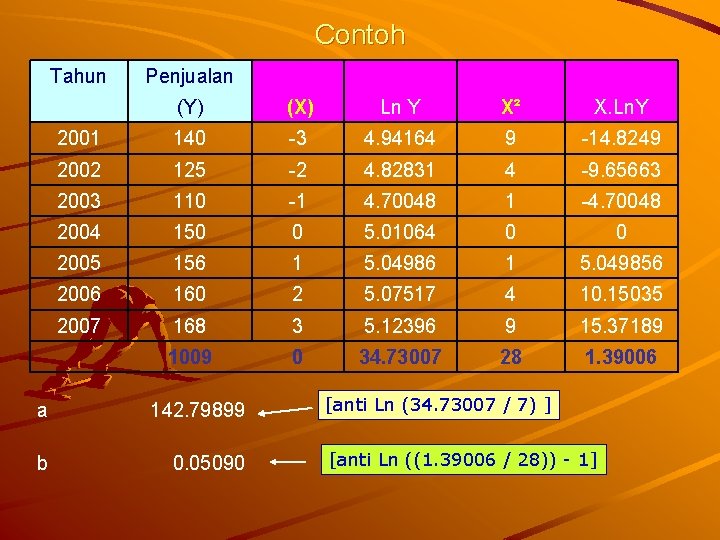
Contoh Tahun Penjualan (Y) (X) Ln Y X² X. Ln. Y 2001 140 -3 4. 94164 9 -14. 8249 2002 125 -2 4. 82831 4 -9. 65663 2003 110 -1 4. 70048 1 -4. 70048 2004 150 0 5. 01064 0 0 2005 156 1 5. 049856 2006 160 2 5. 07517 4 10. 15035 2007 168 3 5. 12396 9 15. 37189 1009 0 34. 73007 28 1. 39006 a 142. 79899 b 0. 05090 [anti Ln (34. 73007 / 7) ] [anti Ln ((1. 39006 / 28)) - 1]

Contoh Persamaan tren eksponensial Y = a(1 + b)x Y = 142. 79899 (1 + 0. 05090)x Peramlan penjualan tahun 2009 ( X =5 ), sebesar : Y = 142. 79899 (1 + 0. 05090)5 Y = 142. 79899 (1. 281749) Y = 144. 08074 Jadi perkiraan unit terjual tahun 2009 sebesar 144 unit

Memilih Tren yang baik Dalam memilih metode tren yang baik dapat digunakan ukuran ketepatan Ukuran ketepatan Adalah seberapa tepat sebuah alat peramalan tersebut menduga kejadian yang sebenarnya Alat ukur yaitu ∑(Y – Y’)2 paling kecil
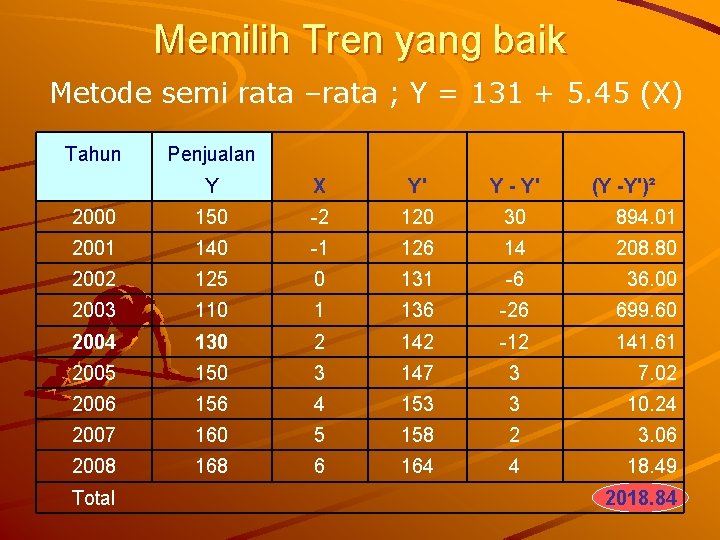
Memilih Tren yang baik Metode semi rata –rata ; Y = 131 + 5. 45 (X) Tahun Penjualan Y X Y' Y - Y' 2000 150 -2 120 30 894. 01 2001 140 -1 126 14 208. 80 2002 125 0 131 -6 36. 00 2003 110 1 136 -26 699. 60 2004 130 2 142 -12 141. 61 2005 150 3 147 3 7. 02 2006 156 4 153 3 10. 24 2007 160 5 158 2 3. 06 2008 168 6 164 4 18. 49 Total (Y -Y')² 2018. 84
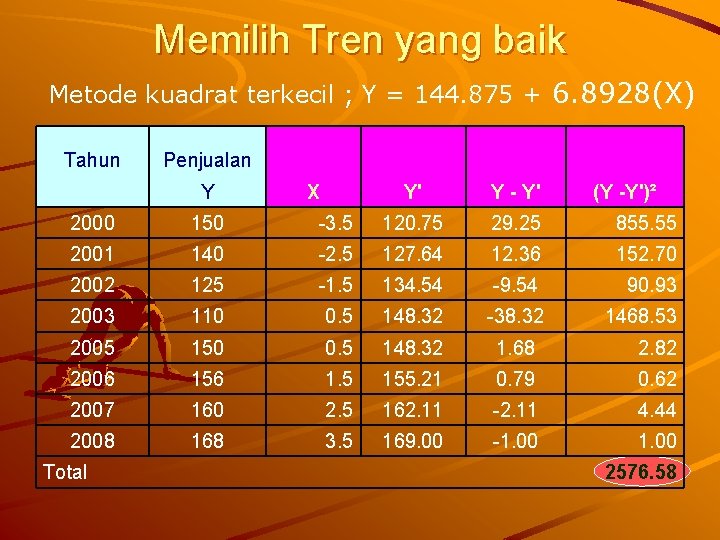
Memilih Tren yang baik Metode kuadrat terkecil ; Y = 144. 875 + 6. 8928(X) Tahun Penjualan Y X 2000 150 2001 Y' Y - Y' -3. 5 120. 75 29. 25 855. 55 140 -2. 5 127. 64 12. 36 152. 70 2002 125 -1. 5 134. 54 -9. 54 90. 93 2003 110 0. 5 148. 32 -38. 32 1468. 53 2005 150 0. 5 148. 32 1. 68 2. 82 2006 156 1. 5 155. 21 0. 79 0. 62 2007 160 2. 5 162. 11 -2. 11 4. 44 2008 168 3. 5 169. 00 -1. 00 Total (Y -Y')² 2576. 58
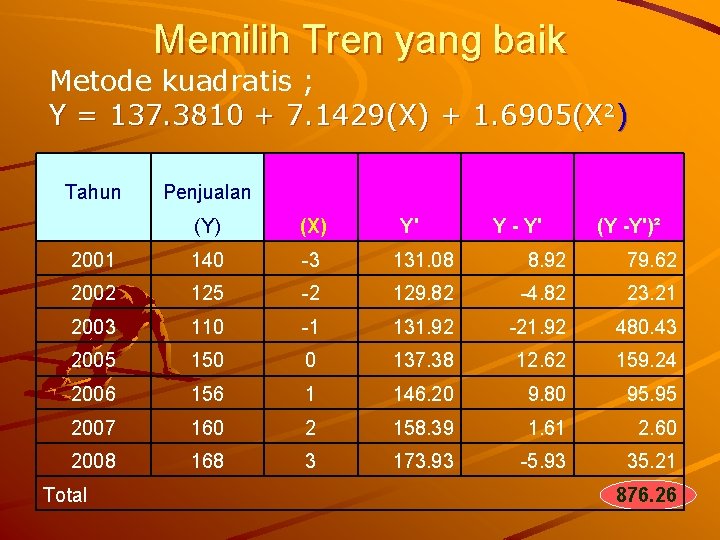
Memilih Tren yang baik Metode kuadratis ; Y = 137. 3810 + 7. 1429(X) + 1. 6905(X 2) Tahun Penjualan (Y) (X) 2001 140 -3 131. 08 8. 92 79. 62 2002 125 -2 129. 82 -4. 82 23. 21 2003 110 -1 131. 92 -21. 92 480. 43 2005 150 0 137. 38 12. 62 159. 24 2006 156 1 146. 20 9. 80 95. 95 2007 160 2 158. 39 1. 61 2. 60 2008 168 3 173. 93 -5. 93 35. 21 Total Y' Y - Y' (Y -Y')² 876. 26
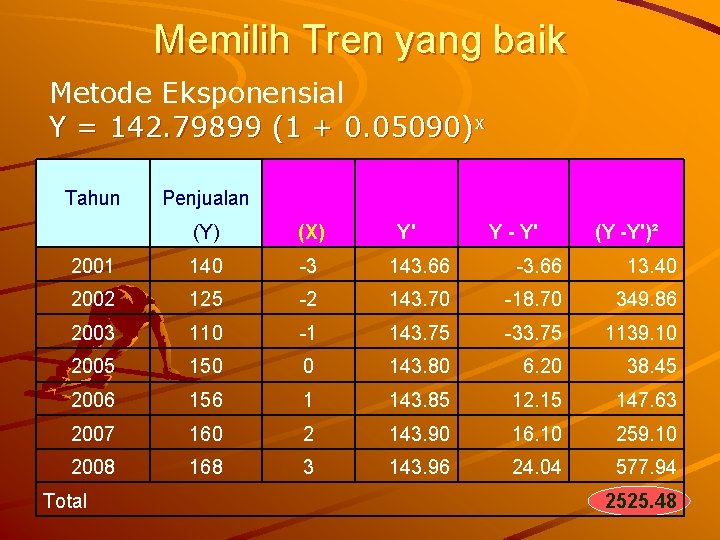
Memilih Tren yang baik Metode Eksponensial Y = 142. 79899 (1 + 0. 05090)x Tahun Penjualan (Y) (X) 2001 140 -3 143. 66 -3. 66 13. 40 2002 125 -2 143. 70 -18. 70 349. 86 2003 110 -1 143. 75 -33. 75 1139. 10 2005 150 0 143. 80 6. 20 38. 45 2006 156 1 143. 85 12. 15 147. 63 2007 160 2 143. 90 16. 10 259. 10 2008 168 3 143. 96 24. 04 577. 94 Total Y' Y - Y' (Y -Y')² 2525. 48

Memilih Tren yang baik Kesimpulan : – Tren semi rata – rata Kuadrat terkecil kuadratis Eksponensial : : 2018. 84 2576. 58 876. 26 2525. 48 Metode kuadratis yang lebih kecil, Jadi metode yang cocok untuk meramalkan penjualan adalah metode kuadratis

Berlanjut ke pembahasan Analisis Variasi musim
- Slides: 26