Statistika D 360 P 03 Z akademick rok

Statistika (D 360 P 03 Z) akademický rok 2004/2005 doc. RNDr. Karel Zvára, CSc. KPMS MFF UK karel. zvara@mff. cuni. cz http: //www. karlin. mff. cuni. cz/~zvara/ 221 913 276 II. část 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 1

pravděpodobnost n n n pokus – dobře definovaná situace (postup), který končí jedním z řady výsledků náhodný pokus – pokus, u něhož předem nevíme, který výsledek nastane; předpokládá se stabilita relativních četností možných výsledků náhodný jev – tvrzení o výsledku náhodného pokusu pravděpodobnost náhodného jevu A – číselné vyjádření očekávání, že výsledkem náhodného pokusu bude právě A při velkém počtu opakování pokusu se relativní četnost jevu blíží k jeho pravděpodobnosti 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 2

klasická pravděpodobnost n n nechť každý jev se skládá ze stejně pravděpodobných elementárních jevů (symetrie) celkem M stejně pravděpodobných disjunktních elementárních jevů z nich je MA příznivých jevu A klasická pravděpodobnost 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 3

příklad - hrací kostka n n n n idealizovaná symetrická homogenní kostka každá strana má stejnou pravděpodobnost A – padne šestka B – padne sudé číslo M=6 MA = 1, tedy P(A) = 1/6 MB = 3, tedy P(B) = 3/6 = 1/2 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 4

faktoriál n n n faktoriál n ! = n · (n – 1) · … · 2 · 1 (kolika způsoby lze uspořádat za sebou n rozlišitelných prvků) příklady: 5! = 5 · 4 · 3 · 2 · 1 = 120 1! = 1 0! = 1 kolika způsoby mohu uspořádat za sebou 14 krajů: 14! = 87 178 291 200 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 5

počet kombinací n n kombinační číslo (n nad k) počet k-prvkových podmnožiny o n prvcích nezávisle na jejich pořadí kolika způsoby mohu z pěti knížek vybrat dvě na dovolenou kolika způsoby si mohu vybrat tři knihy? (10) 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 6

příklad – losování otázek (1) n n n student neumí 5 otázek, umí 10 otázek losuje se dvojice otázek z oněch 15 pravděpodobnost, že nezná ani jednu z nich elem. jevy: první losovaná 15 možností, druhá 14, nezáleží na pořadí => dělit 2 příznivé: obě z pěti, které neumí 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 7

příklad – losování otázek (2) n pravděpodobnost, že zná právě jednu n pravděpodobnost, že zná obě otázky n pravděpodobnost, že zná aspoň jednu 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 8

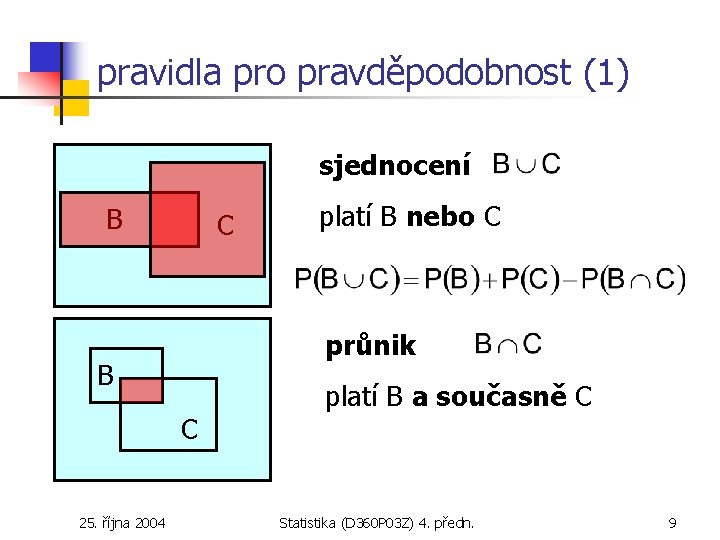
pravidla pro pravděpodobnost (1) sjednocení B C průnik B C 25. října 2004 platí B nebo C platí B a současně C Statistika (D 360 P 03 Z) 4. předn. 9

pravidla pro pravděpodobnost (2) n n neslučitelné jevy: nemohou nikdy současně nastat, platí pro ně podmíněná pravděpodobnost B n C nezávislé jevy: výskyt jednoho neovlivní pravděpodobnost výskytu druhého 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 10

idealizovaný příklad n n n A – jednička ze statistiky, P(A) = 0, 3 B – jednička z matematiky, P(B) = 0, 2 A B – jednička z obou předmětů P(A B) = 0, 1 jsou jedničky nezávislé? NE (0, 2 · 0, 3 = 0, 1? ) jaká je pravděpodobnost, že bude 1 ze statistiky, když už je z matematiky? P(A | B) = P(A B) / P(B) = 0, 1 / 0, 2 = 0, 5 aspoň jedna jednička: P(A)+P(B)-P(A B)=0, 4 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 11

rozdělení náhodné veličiny n n náhodná veličina - číselně vyjádřený výsledek náhodného pokusu diskrétní rozdělení určeno seznamem možných hodnot a jejich pravděpodobnostmi n spojité rozdělení určeno distribuční funkcí n nebo hustotou 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 12

příklad: známka u zkoušky známka k 1 P(X = k) P(Y = k) 2 3 4 0, 3 0, 4 0, 2 0, 1 0, 3 0, 2 jak jedním číslem charakterizovat úroveň? průměr nerozliší X, Y vážený průměr, vahami psti známek populační průměry: X = 1· 0, 3 + 2 · 0, 4 + 3 · 0, 2 + 4 · 0, 1 = 2, 1 Y = 1· 0, 3 + 2 · 0, 3 + 3 · 0, 2 + 4 · 0, 2 = 2, 3 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 13

parametry rozdělení náhodné veličiny n střední hodnota náhodné veličiny X (populační průměr) n n vážený průměr možných hodnot vahami jsou pravděpodobnosti hodnot X = E X = x 1 P(X = x 1) + x 2 P(X = x 2) + … když se použije operátor E na náhodnou veličinu X, spočítá vážený průměr hodnot X, vahami jsou u diskrétního rozdělení pravděpodobnosti těchto hodnot, u spojitého rozdělení integrál 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 14

parametry rozdělení náhodné veličiny n (populační) rozptyl náhodné veličiny X n n vážený průměr čtverců vzdáleností možných hodnot od střední hodnoty 2 X = E(X - X)2=(x 1 - X)2 P(X=x 1)+(x 2 - X)2 P(X=x 2)+… 2 X = E(X - X)2= směrodatná odchylka odmocnina z rozptylu 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 15

příklad: známka u zkoušky známka k 1 P(X = k) P(Y = k) jak vždy jedním číslem 0, 3 0, 4 0, 2 0, 1 2, 1 charakterizovat kolísání (variabilitu)? 2 3 4 0, 3 0, 2 2, 3 vážený průměr čtverců vzdálenosti od střední hodnoty, vahami známky = populační rozptyl 2 X =(1 -2, 1)2· 0, 3 + (2 -2, 1)2· 0, 4 + (3 -2, 1)2· 0, 2 + (4 -2, 1)2· 0, 1 = 0, 89 = 0, 9432 2 Y = (1 -2, 3)2 · 0, 2 +. . . = 1, 21 = 1, 12 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 16

vlastnosti střední hodnoty a rozptylu n n n X, Y – náhodné veličiny a+b. X = E (a+b. X ) = a + b EX = a + b X X+Y = E (X + Y) = E X + E Y = X + Y 2 X+Y = 2 X + 2 Y + 2 XY XY = E(X - X )(Y - Y ) kovariance X, Y = (x 1 - X)(y 1 - Y)P(X=x 1, Y=y 1) + … (všechny dvojice) jsou-li X, Y nezávislé, pak XY = 0, tedy 2 X + Y = 2 X + 2 Y rozptyl součtu = součet rozptylů 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 17

alternativní (nula-jedničkové) rozděl. n diskrétní, má jediný parametr P(X=1) = , P(X=0) = 1 - (0< <1) X - kolikrát v jednom pokusu došlo k události, která má pravděpodobnost střední hodnota X (populační průměr): n (populační) rozptyl: n n n 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 18

binomické rozdělení bi(n , ) (1) n n n diskrétní rozdělení, parametry n, n nezávislých pokusů v každém zdar s pravděpodobností , nezdar s pravděpodobností 1 - X - celkový počet zdarů má binomické rozdělení s parametry n a (0 1) je to součet n nezávislých náhodných veličin s alternativním rozdělením 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 19

binomické rozdělení bi(n , ) (2) n s pstí n n k-krát kolikrát zvolit místo pro Z, ostatní N, nezávisí na pořadí umisťování Z (kombinační číslo) 25. října 2004 Statistika (D 360 P 03 Z) 4. předn. 20