STATISTIKA ANALISIS REGRESI NON LINEAR DAN REGRESI BERGANDA

SUB POKOK BAHASAN • • Hubungan fungsional nonlinear Analisis regresi non linear Selang penaksiran koefisien regresi Analisis regresi linear tiga variabel

Regresi linier berganda • Regresi linier berganda berupaya mencari hubungan fungsional antara beberapa variabel (xi) dengan variabel y • Y=a +a x +…. . a x 0 1 1 2 2 r r

Galat regresi • Hubungan antara data pengamatan yi=a 0+a 1 x 1 i+a 2 x 2 i+……+arxri+ei ei=yi-a 0 -a 1 x 1 i-a 2 x 2 i-……. -arxri • Jumlah kuadrat galat

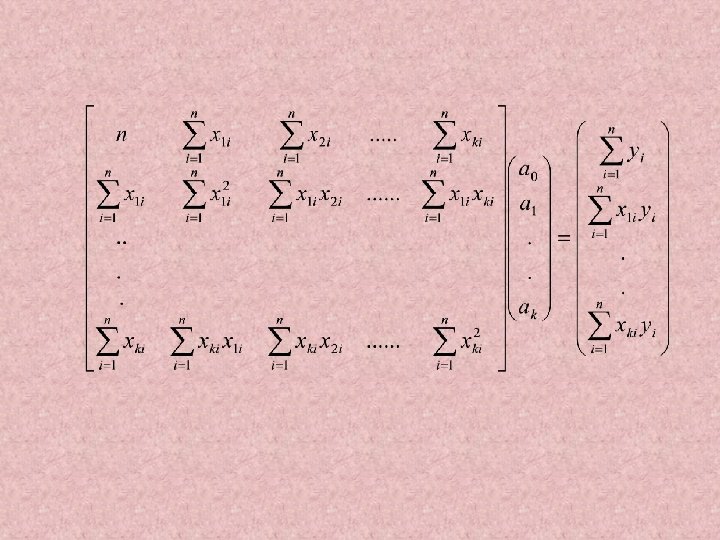
Jumlah kuadrat minimum Akan didapat k+1 persamaan simultan

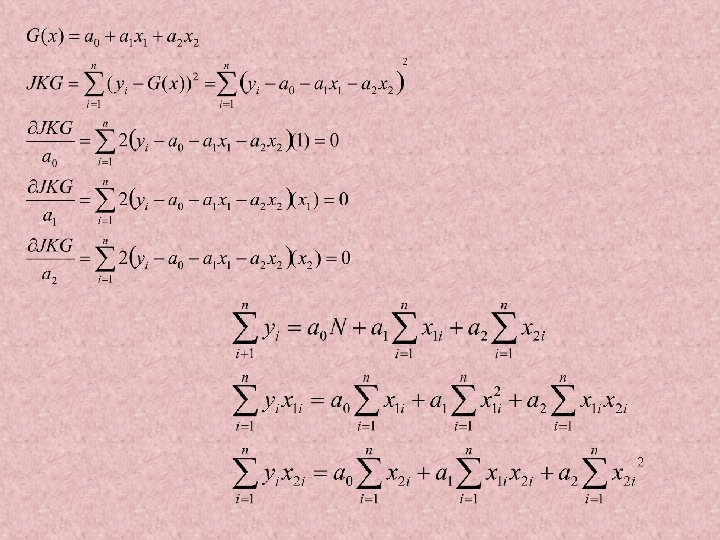
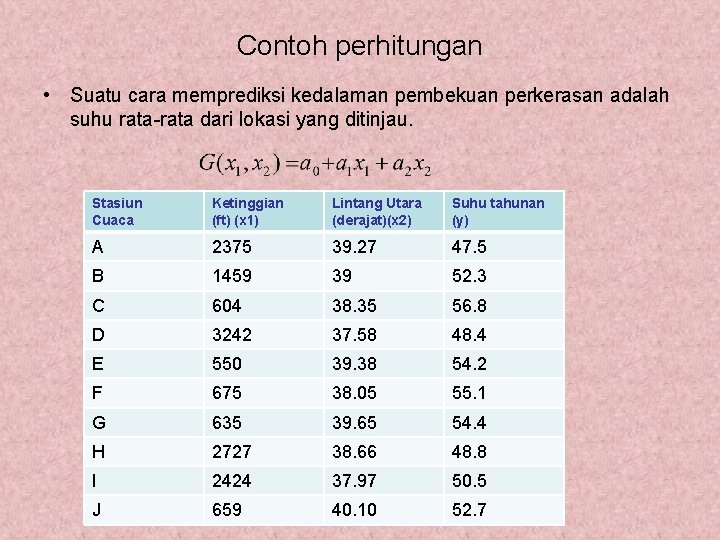
Contoh perhitungan • Suatu cara memprediksi kedalaman pembekuan perkerasan adalah suhu rata-rata dari lokasi yang ditinjau. Stasiun Cuaca Ketinggian (ft) (x 1) Lintang Utara (derajat)(x 2) Suhu tahunan (y) A 2375 39. 27 47. 5 B 1459 39 52. 3 C 604 38. 35 56. 8 D 3242 37. 58 48. 4 E 550 39. 38 54. 2 F 675 38. 05 55. 1 G 635 39. 65 54. 4 H 2727 38. 66 48. 8 I 2424 37. 97 50. 5 J 659 40. 10 52. 7

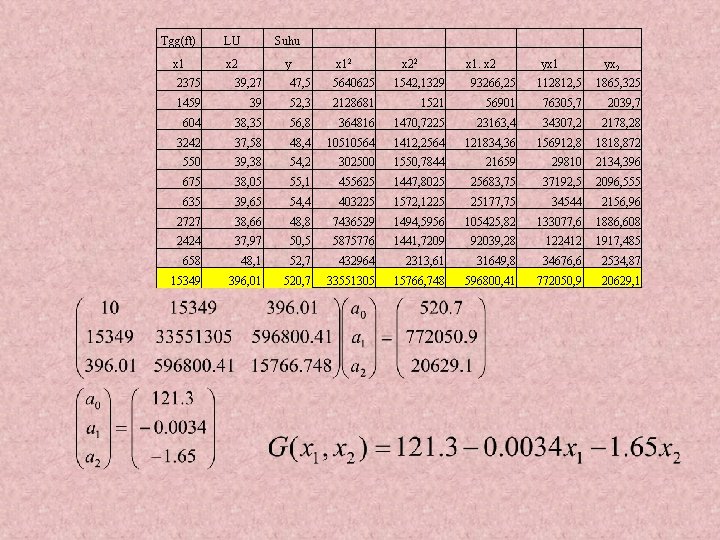
Tgg(ft) LU Suhu x 1 x 2 y x 12 x 22 x 1. x 2 yx 1 yx 2 2375 39, 27 47, 5 5640625 1542, 1329 93266, 25 112812, 5 1865, 325 1459 39 52, 3 2128681 1521 56901 76305, 7 2039, 7 604 38, 35 56, 8 364816 1470, 7225 23163, 4 34307, 2 2178, 28 3242 37, 58 48, 4 10510564 1412, 2564 121834, 36 156912, 8 1818, 872 550 39, 38 54, 2 302500 1550, 7844 21659 29810 2134, 396 675 38, 05 55, 1 455625 1447, 8025 25683, 75 37192, 5 2096, 555 635 39, 65 54, 4 403225 1572, 1225 25177, 75 34544 2156, 96 2727 38, 66 48, 8 7436529 1494, 5956 105425, 82 133077, 6 1886, 608 2424 37, 97 50, 5 5875776 1441, 7209 92039, 28 122412 1917, 485 658 48, 1 52, 7 432964 2313, 61 31649, 8 34676, 6 2534, 87 15349 396, 01 520, 7 33551305 15766, 748 596800, 41 772050, 9 20629, 1

Ketidaktepatan model linear • Jika jumlah kuadrat galat dari regresi linier sangat besar sehingga model regresi tidak signifikan, maka perlu dilakukan pengujian ketidakcocokan model linier • Pengujian dilakukan dengan menghitung jumlah kuadrat tengah galat untuk nilai pengamatan dalam kelompok peubah x(sebut kuadrat galat murni) , dibandingkan dengan kuadrat tengah seluruh galat. Selisih dari kuadrat galat ini menjadi kuadrat galat akibat kekurang-cocokkan model.

• Ambil k-kelompok amatan. Kuadrat tengah galat pada kelompok ke-i (i = 1 s/d k) adalah: Kuadrat tengah gabungan akibat ketidak cocokkan adalah Dengan membandingkan kuadrat tengah ini dapat dilihat apakah ketidak cocokan ini cukup signifikan

Model non linier • Ada dua pendekatan yang biasa dilakukan yaitu transformasi ke bentuk linear (linearisasi) dan membuat model fungsi polynomial yang melibatkan peubah pangkat dua atau lebih • Transformasi yang sering dipakai adalah: – Fungsi pangkat – Fungsi invers – Fungsi hiperbolik – Fungsi eksponen

Linearisasi

Model polinomial • Model regresi polinomial untuk satu peubah pangkat dua adalah

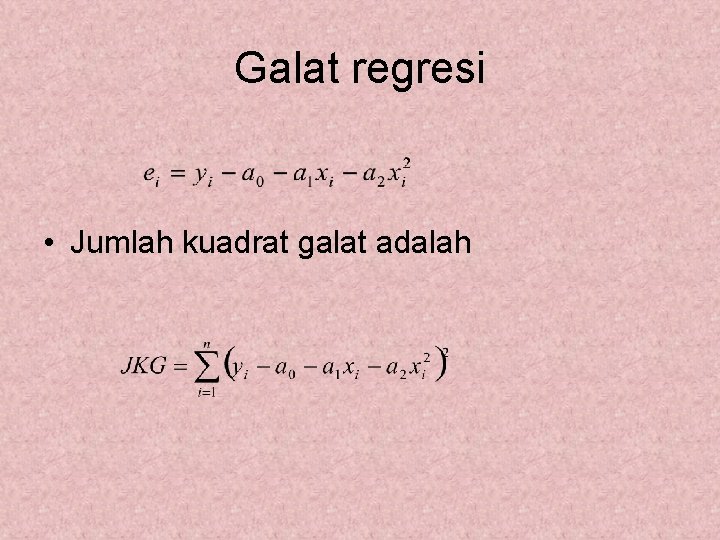
Galat regresi • Jumlah kuadrat galat adalah

Kuadrat galat minimum • Untuk meminimumkan kuadrat galat dilakukan penurunan

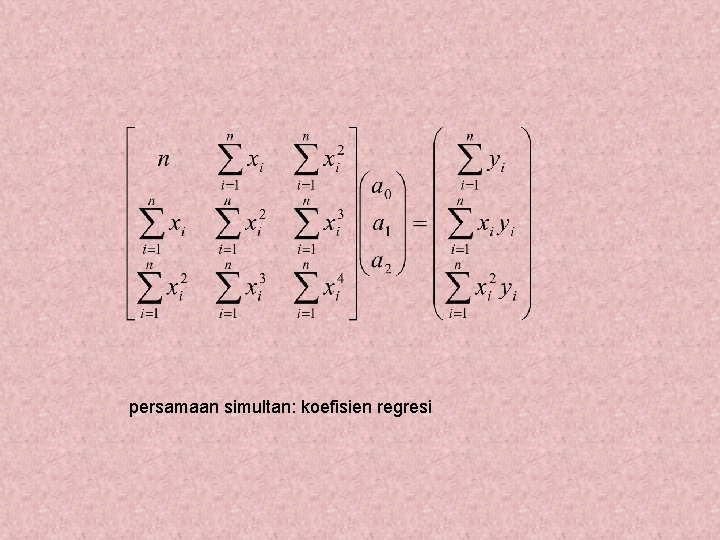
persamaan simultan: koefisien regresi

Contoh untuk regresi polinomial pangkat dua, pengaruh penambahan Abu Terbang terhadap kuat tekan beton

Persamaan simultan Solusi persamaan diatas adalah Persamaan regresi menjadi