STATISTIKA 2 9 Regresi Korelasi MATERI KULIAH STATISTIKA

STATISTIKA 2 9. Regresi & Korelasi MATERI KULIAH STATISTIKA INDUKTIF ILMU EKONOMI UNIVERSITAS GUNADARMA 2018 1 OLEH: RISKAYANTO

PENGANTAR Gagasan dan konsep regresi ditetapkan oleh Sir Francis Galton (1822 – 1911). Persamaan Regresi: Adalah suatu persamaan matematika yang memungkinkan untuk dilakukannya estimasi nilai suatu peubah tak-bebas (dependent variable) dari nilai peubah bebas (independent variable). Korelasi: Adalah sebuah nilai yang menggambarkan tingkat keeratan hubungan antara dua variabel yang diamati → misalnya antara variabel dependen dan variabel independen. 2

PENGANTAR Perbedaan antara Regresi dan Korelasi: Regresi → bentuk hubungan antara variabel yang mempengaruhi variabel lain atau bentuk hubungan antara variabel independen (biasa disimbolkan dengan X) terhadap variabel dependen (biasa disimbolkan dengan Y). Korelasi → besarnya derajat atau tingkat hubungan dan arah hubungan antara variabel yang satu dengan variabel lainnya. 3

HUBUNGAN ANTARA X DAN Y Beberapa kemungkinan hubungan yang dapat terjadi antara X dan Y pada persamaan regresi: Linier searah Linier berlawanan arah Curvilinier searah Curvilinier berlawanan arah Linier berlawanan dengan lebih menyebar Tidak ada hubungan 4

HUBUNGAN ANTARA X DAN Y Diagram pencar: 5

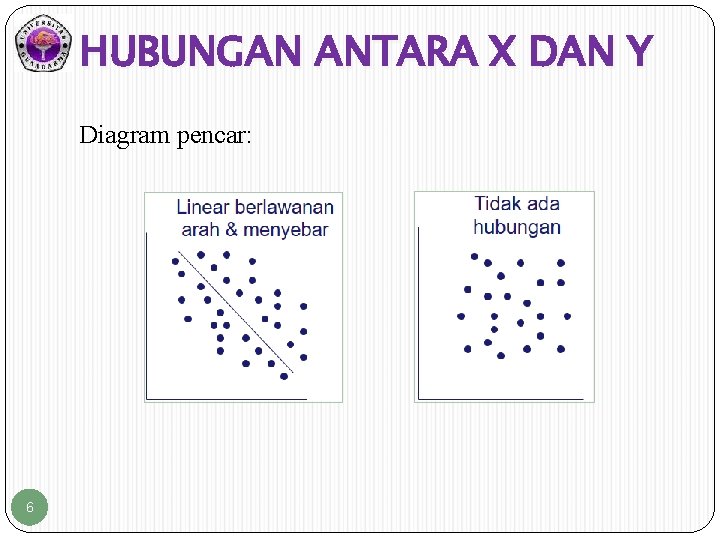
HUBUNGAN ANTARA X DAN Y Diagram pencar: 6

REGRESI LINIER Bentuk umum persamaan regresi linier sederhana Ŷ = a + b. X Ŷ = β 0 + β 1. X Keterangan: Ŷ = variabel tak bebas (independen) X = variabel bebas (dependen) a atau β 0 = konstanta b atau β 1 = kemiringan (slope) garis regresi 7

REGRESI LINIER Persamaan regresi lain Regresi linier berganda: Ŷ = β 0 + β 1. X + β 2. X + β 3. X + …. . + βn. Xn n = jumlah peubah dependen Regresi non-linier: Ŷ = ab. X 8 Log Ŷ = log a + (log b). X

REGRESI LINIER SEDERHANA Model matematis bagi regresi linier sederhana (RLS) biasa diestimasi dengan metode kuadrat terkecil (OLS – Ordinary Least Square). Bentuk umum model regresi linier sederhana adalah sbb: Y = a + b. X dengan penjelasan simbol seperti pada slide sebelumnya Analisis RLS pada dasarnya dilakukan untuk mengestimasi dua macam besaran dalam model tersebut, yaitu: 9 v. Konstanta a atau ß 0.

REGRESI LINIER SEDERHANA Dalam metode OLS, estimasi besaran-besaran model regresi menunjukkan: v. Konstanta a atau ß 0: merupakan intersep (intercept) antara garis regresi dengan sumbu tegak (sumbu Y). v. Parameter regresi ß 1: merupakan tingkat kemiringan (slope) garis regresi. Estimasi model hubungan antara Y dan X selalu dibuat dalam kerangka bentuk garis lurus (linier). Jika hubungan tersebut tidak linier, maka harus ditransformasi terlebih dulu sehingga hubungan menjadi linier (misalnya nilai-nilai variabel diubah bentuknya menjadi logaritma). 10

REGRESI LINIER SEDERHANA Konsep Model OLS: 11

REGRESI LINIER SEDERHANA Prinsip dasar estimasi model RLS dengan model OLS adalah meminimalkan jumlah eror terhadap pengamatan nyata (riil). lihat gambar slide sebelumnya. Estimasi garis regresi dengan jumlah eror paling minimal (kecil) dikatakan sebagai garis (model) regresi dengan estimasi yang paling fit. Estimasi kesalahan baku pada model (standard error of estimation) mengikuti logika dengan langkah-langkah sebagai berikut: 12

REGRESI LINIER SEDERHANA Standard Error of Estimation (Se) (lanjutan…): 13

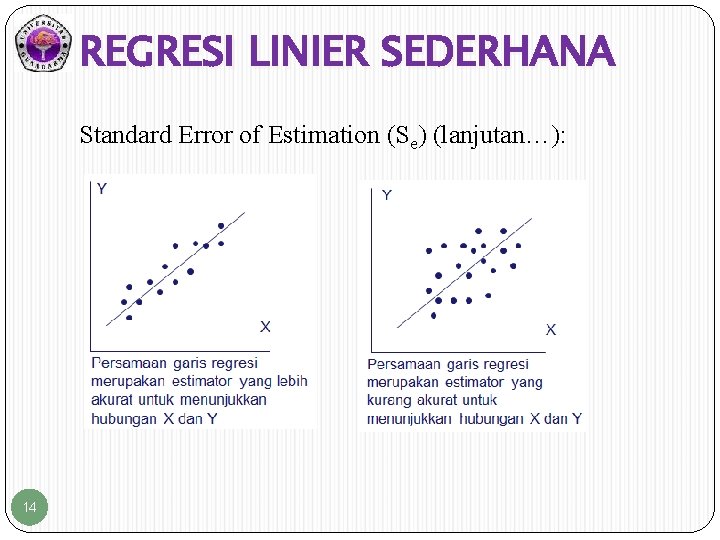
REGRESI LINIER SEDERHANA Standard Error of Estimation (Se) (lanjutan…): 14

REGRESI LINIER SEDERHANA Penentuan koefisien-koefisien regresi (konstanta dan parameter regresi): 15

REGRESI LINIER SEDERHANA Untuk perhitungan manual, rumus kerja yang digunakan bisa mengikuti manipulasi matematis sbb: sedangka n jadi 16 di mana, n = banyaknya pasangan data yi = nilai peubah tak bebas Y ke-i xi = nilai peubah bebas ke-i

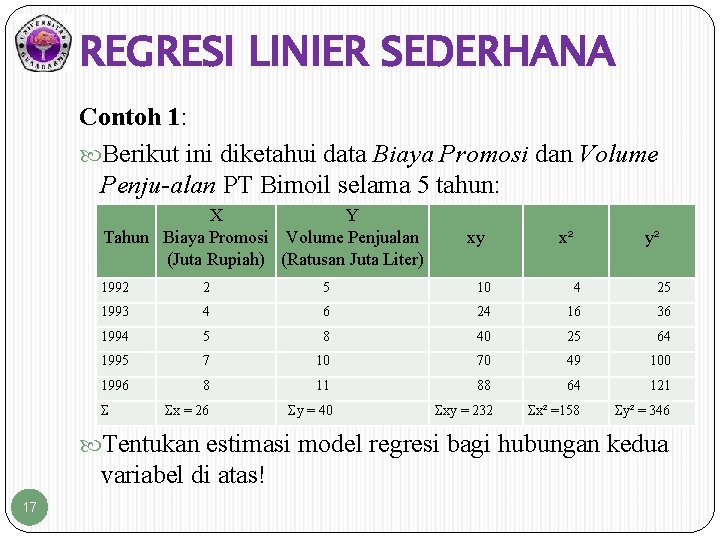
REGRESI LINIER SEDERHANA Contoh 1: Berikut ini diketahui data Biaya Promosi dan Volume Penju-alan PT Bimoil selama 5 tahun: X Y Tahun Biaya Promosi Volume Penjualan (Juta Rupiah) (Ratusan Juta Liter) xy x² y² 1992 5 10 4 25 1993 4 6 24 16 36 1994 5 8 40 25 64 1995 7 10 70 49 100 1996 8 11 88 64 121 x = 26 y = 40 xy = 232 x² =158 y² = 346 Tentukan estimasi model regresi bagi hubungan kedua variabel di atas! 17

REGRESI UNTUK PERAMALAN Contoh 2: Berdasarkan hasil pemodelan regresi pada contoh soal nomer 1, perkirakan besarnya volume penjualan yang akan dibuat oleh PT Bimoil jika perusahaan membelanjakan biaya untuk promosi sebesar Rp. 10 juta! 18

ANALISIS RESIDUAL Residual adalah error yang terjadi antara pengamatan data riil dengan garis regresi. Dengan kata lain, residual menunjukkan perbedaan antara y prediksi dengan y aktualnya. Tujuan analisis residual adalah untuk menguji sebagian atau seluruh asumsi yang mendasari regresi, yaitu: v. Model adalah linier v. Suku error memiliki varians yang konstan v. Semua suku error independen v. Suku error terdistribusi normal 19

ANALISIS RESIDUAL Bentuk-bentuk plot residual: 20

ANALISIS RESIDUAL Inferensia pada uji terhadap koefisien-koefisien regresi: H 0: ßi = 0 H 0: tidak ada pengaruh yang signifikan dari X terhadap Y H 1: ßi ≠ 0 H 1: ada pengaruh yang signifikan dari X terhadap Y 21

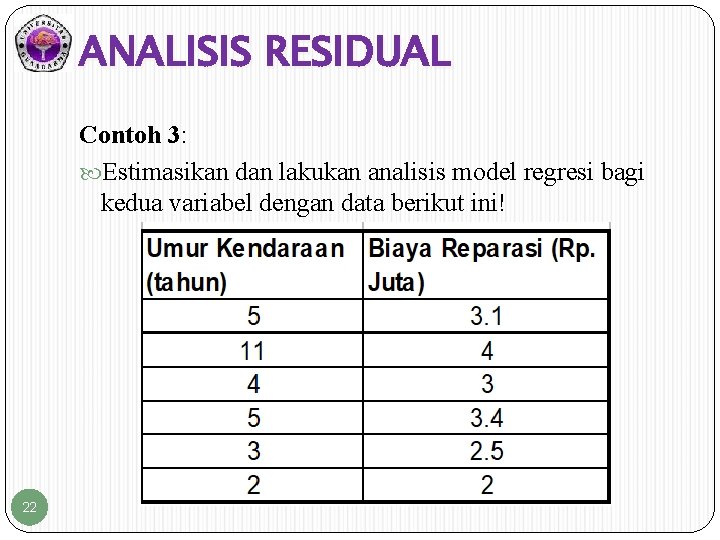
ANALISIS RESIDUAL Contoh 3: Estimasikan dan lakukan analisis model regresi bagi kedua variabel dengan data berikut ini! 22

KORELASI KOEFISIEN KORELASI (r) Sebuah besaran yang menunjukkan keeratan antar variabel dan tidak memiliki satuan Nilai r berkisar antara – 1 hingga +1 Tanda koefisien korelasi menunjukkan arah hubungannya Hanya mencerminkan keeratan hubungan linier dari dua variabel yang terlibat Bersifat simetris (bolak-balik) Variabel yang terlibat tidak harus dalam status sebagai variabel dependen dan independen atau sebaliknya. 23

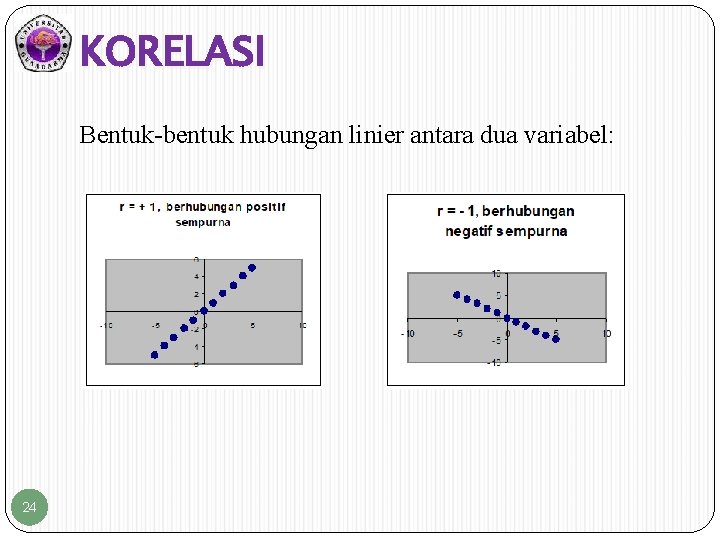
KORELASI Bentuk-bentuk hubungan linier antara dua variabel: 24

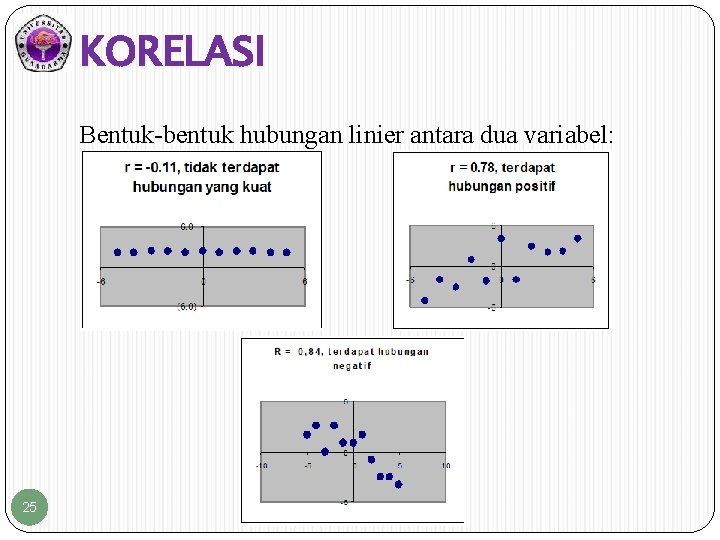
KORELASI Bentuk-bentuk hubungan linier antara dua variabel: 25

KORELASI Inferensia terhadap koefisien korelasi populasi (ρ) Hipotesis yang digunakan adalah: H 0: ρ = 0 H 1: ρ ≠ 0 Interpretasi hipotesis: H 0: ada hubungan yang signifikan antara X dan Y H 1: tidak ada hubungan yang signifikan antara X dan Y 26

KORELASI Koefisien korelasi (r) dihitung dengan menggunakan rumus: Selanjutnya, koefisien determinasi sampel (R) diperoleh dengan mengkuadratkan koefisien korelasinya: 27

KORELASI Koefisien determinasi (R) merupakan ukuran ketepatan/ kecocokan garis regresi yang dibuat dari hasil estimasi ter-hadap sekelompok data hasil observasi. Semakin besar nilai R, semakin bagus garis regresi yang terbentuk, demikian juga sebaliknya. Untuk mengukur proporsi dari jumlah variasi yang dapat diterangkan oleh model regresi atau untuk mengukur besar sumbangan (kontribusi) variabel X terhadap variasi pada variabel Y. Nilai R berkisar antara 0 dan 1. 28

KORELASI Contoh 4: Dari soal pada Contoh 1, hitunglah koefisien korelasi (r) dan koefisien determinasi (R) antara Biaya Promosi dan Volume Penjualan! 29

REGRESI LINIER BERGANDA Regresi berganda merupakan salah satu analisa statistika yang mempelajari hubungan antara satu (1) variabel depen-den dengan lebih dari satu (<1) variabel independen. Tujuannya adalah untuk mengetahui variabel independen yang paling berpengaruh terhadap variabel dependen. Sebelum melakukan analisis regresi, seorang peneliti terlebih dahulu harus memastikan: v. Data yang ada bersifat metrik. Data non-metrik dapat 30 diolah dengan regresi berganda, namun dengan teknik yang berbeda. v. Sudah ditentukan mana variabel dependen dan mana

REGRESI LINIER BERGANDA Persamaan regresi linier berganda akan meliputi unsur- unsur sebagai berikut: v. Y prediksi (Ŷ) va atau β 0 vβ 1 dan β 2 X 2 v. X 1 dan X 2 = estimasi nilai variabel dependen = konstanta (intersep) = slope untuk variabel X 1 dan = variabel independen ke-1 dan ke-2 Bentuk umum model regresi linier berganda dengan n variabel independen adalah: Ŷ = β 0 + β 1. X + β 2. X + β 3. X + …. . + βn. Xn 31

REGRESI LINIER BERGANDA Estimasi koefisien-koefisien persamaan regresi linier berganda diselesaikan dengan menyelesaikan tiga persamaan normal berikut: i. pertama: ii. kedua: iii. ketiga: 32

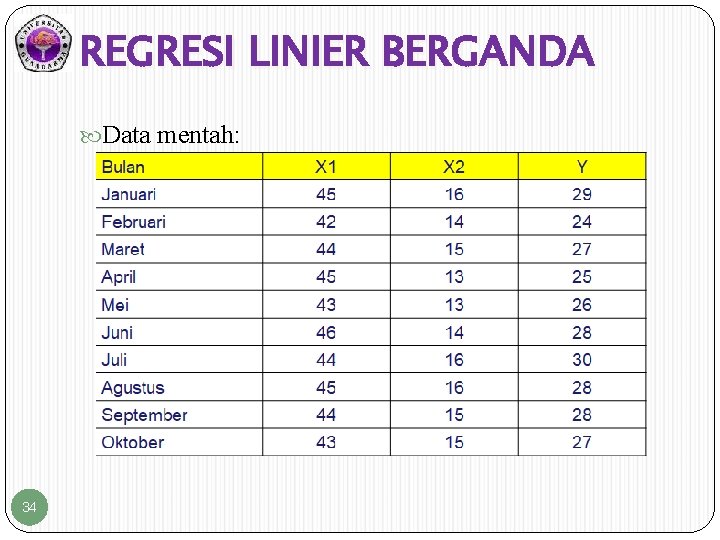
REGRESI LINIER BERGANDA Contoh 5: Pada dua slide berikutnya disajikan data Y berupa volume penjualan sepeda motor (dalam juta unit) yang dihubungkan dengan data variabel X 1 berupa biaya promosi (dalam juta Rupiah/bulan) dan variabel X 2 berupa biaya penambahan aksesoris (dalam ratusan ribu Rupiah/bulan). Estimasikan model regresi linier berganda antara variabel-variabel tersebut! 33

REGRESI LINIER BERGANDA Data mentah: 34

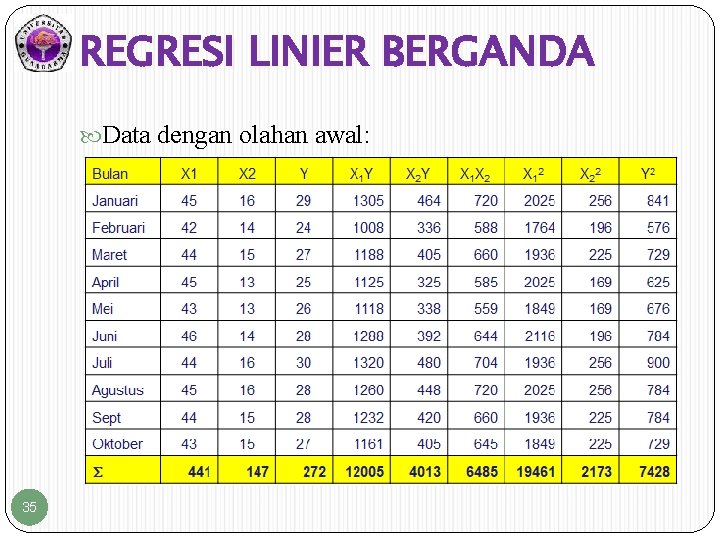
REGRESI LINIER BERGANDA Data dengan olahan awal: 35

REGRESI LINIER BERGANDA 36