STATISTIK II Pertemuan 5 6 Metode Sampling dan

STATISTIK II Pertemuan 5 -6: Metode Sampling dan Interval Konfidensi Dosen Pengampu MK: Evellin Lusiana, S. Si, M. Si

Materi n n Metode sampling Interval konfidensi

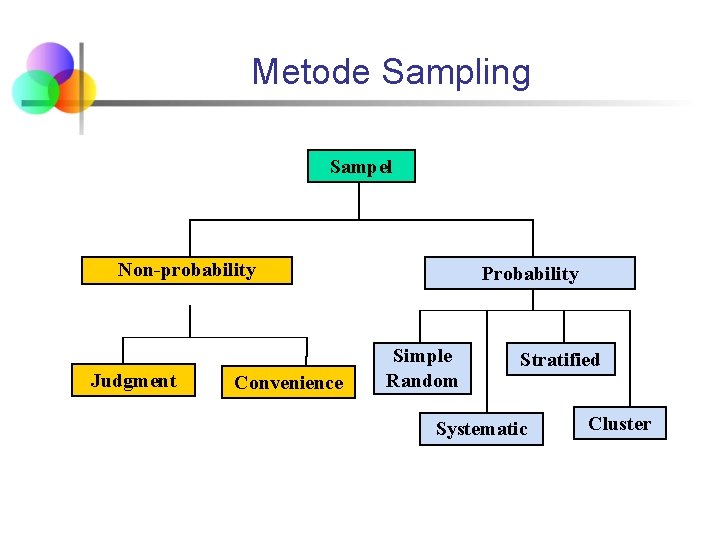
Metode Sampling Sampel Non-probability Judgment Convenience Probability Simple Random Stratified Systematic Cluster

Nonprobability Sampling n Dalam sampling non-probability, objek yang dijadikan sampel dipilih tanpa memperhatikan nilai probabilitasnya n n Convenience sampling objek dipilih karena alasan kemudahan seperti hemat biaya dan mudah diperoleh Judgment sampling objek dipilih berdasarkan opini para ahli/expert

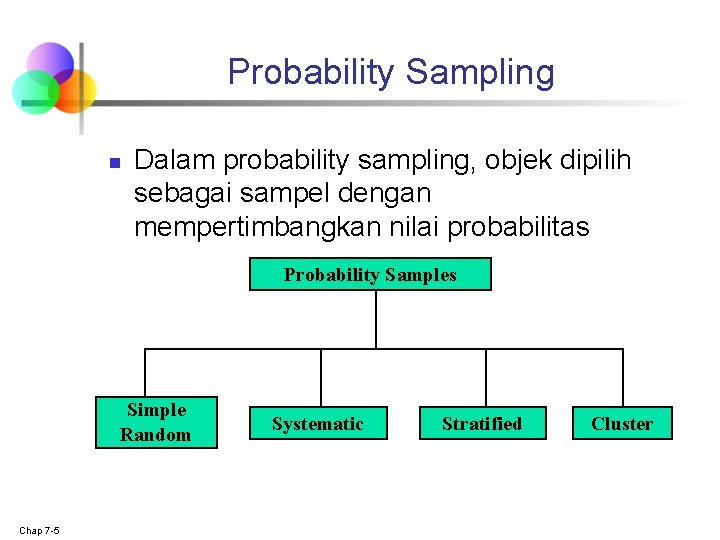
Probability Sampling n Dalam probability sampling, objek dipilih sebagai sampel dengan mempertimbangkan nilai probabilitas Probability Samples Simple Random Chap 7 -5 Systematic Stratified Cluster

Simple Random Sampling n n Chap 7 -6 Setiap individu dalam populasi memiliki kesempatan yg sama untuk terpilih sbg sampel Sampel diperoleh secara acak/random dengan bantuan tabel bilangan acak atau pembangkit bilangan acak

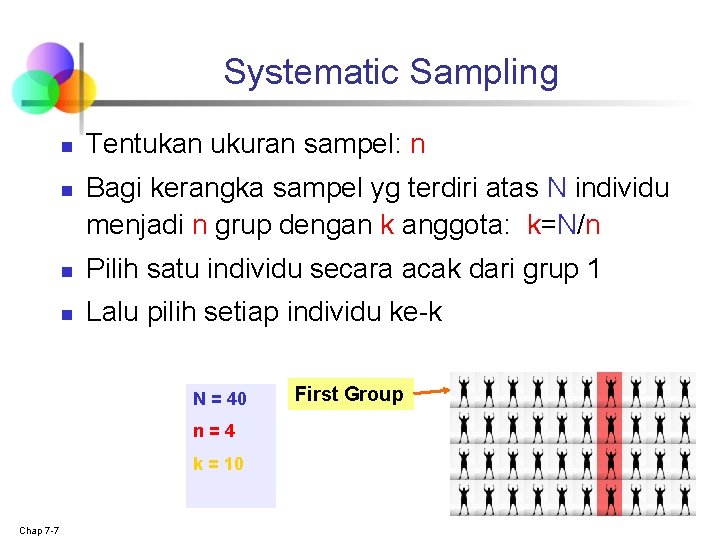
Systematic Sampling n n Tentukan ukuran sampel: n Bagi kerangka sampel yg terdiri atas N individu menjadi n grup dengan k anggota: k=N/n n Pilih satu individu secara acak dari grup 1 n Lalu pilih setiap individu ke-k N = 40 n=4 k = 10 Chap 7 -7 First Group

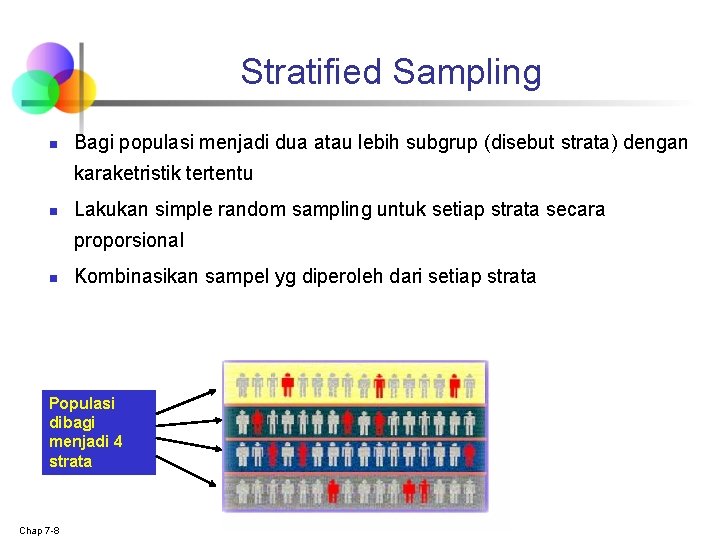
Stratified Sampling n Bagi populasi menjadi dua atau lebih subgrup (disebut strata) dengan karaketristik tertentu n Lakukan simple random sampling untuk setiap strata secara proporsional n Kombinasikan sampel yg diperoleh dari setiap strata Populasi dibagi menjadi 4 strata Chap 7 -8

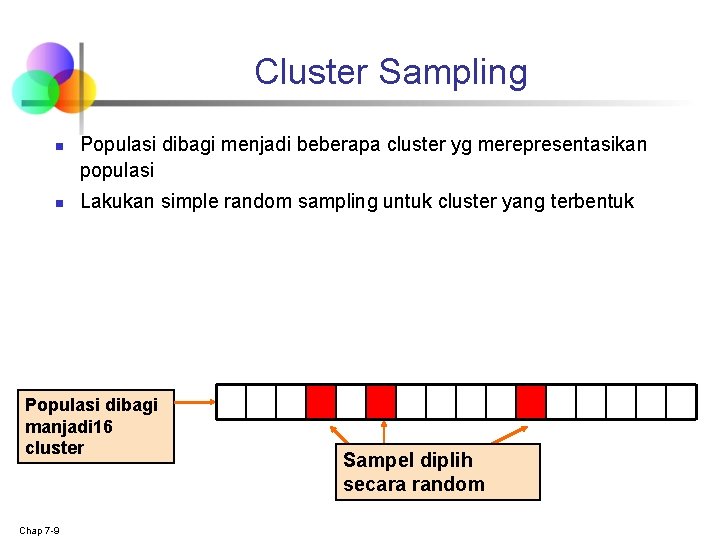
Cluster Sampling n n Populasi dibagi menjadi beberapa cluster yg merepresentasikan populasi Lakukan simple random sampling untuk cluster yang terbentuk Populasi dibagi manjadi 16 cluster Chap 7 -9 Sampel diplih secara random

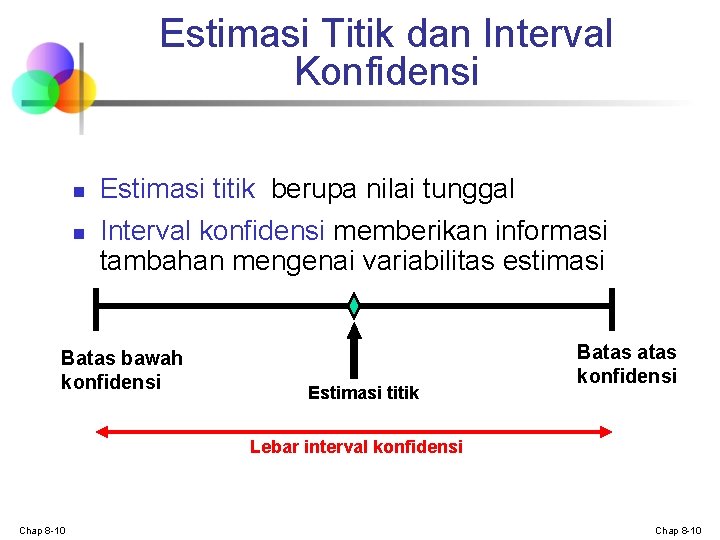
Estimasi Titik dan Interval Konfidensi n n Estimasi titik berupa nilai tunggal Interval konfidensi memberikan informasi tambahan mengenai variabilitas estimasi Batas bawah konfidensi Estimasi titik Batas konfidensi Lebar interval konfidensi Chap 8 -10

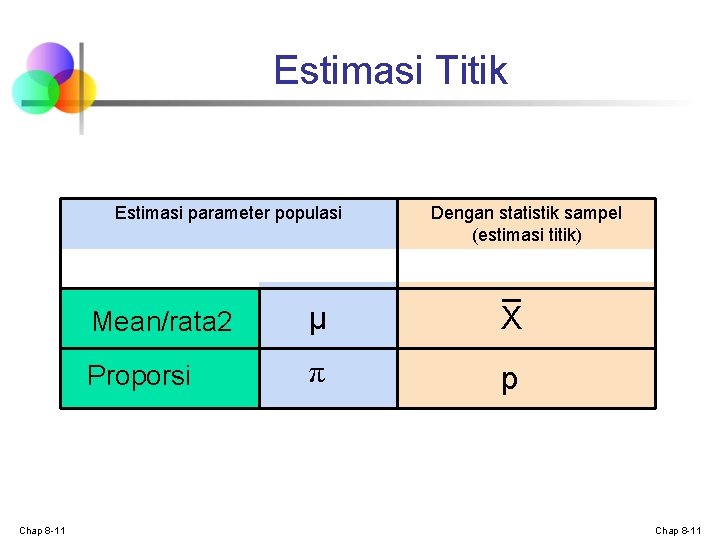
Estimasi Titik Estimasi parameter populasi Chap 8 -11 Dengan statistik sampel (estimasi titik) Mean/rata 2 μ X Proporsi π p Chap 8 -11

Interval Konfidensi n Suatu interval berupa range nilai yang n n n Chap 8 -12 Memperhatikan variasi statistik masing 2 sampel berdasarkan informasi dari 1 sampel Memberi informasi kedekatan nilai estimasi dengan nilai parameter sebenarnya Dinyatakan sebagai level konfidensi (tingkat kepercayaan) n Misal, 95% konfidensi atau 99% konfidensi n Tidak pernah 100% konfidensi Chap 8 -12

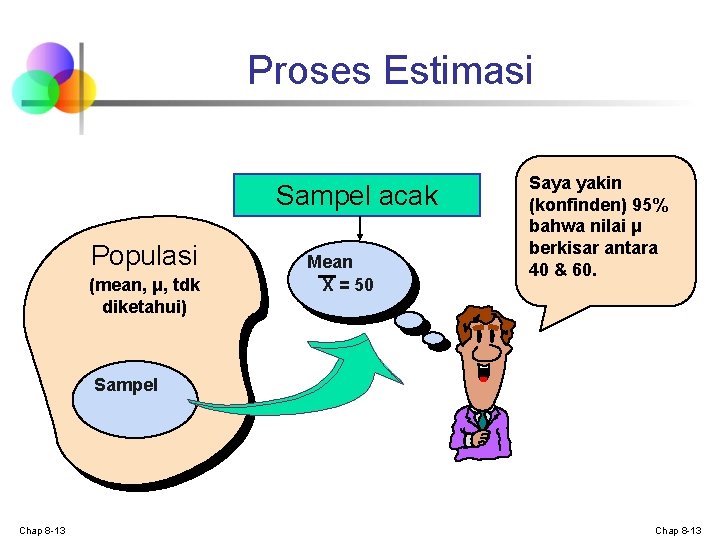
Proses Estimasi Sampel acak Populasi (mean, μ, tdk diketahui) Mean X = 50 Saya yakin (konfinden) 95% bahwa nilai μ berkisar antara 40 & 60. Sampel Chap 8 -13

Rumus Umum n Rumus umum untuk semua interval konfidensi: Estimasi titik± (titik kritis)(Standar Error) Di mana: • Estimasi titik statistik sampel untuk menduga parameter populasi yg dikehendaki • Titik kritis nilai distribusi sampling dari estimasi titik dengan tingkat konfindensi tertentu • Standard Error standar deviasi dari estimasi titik Chap 8 -14

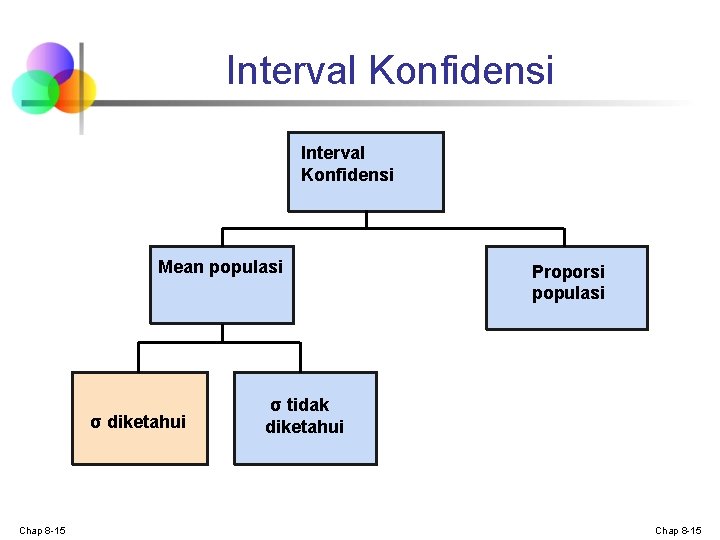
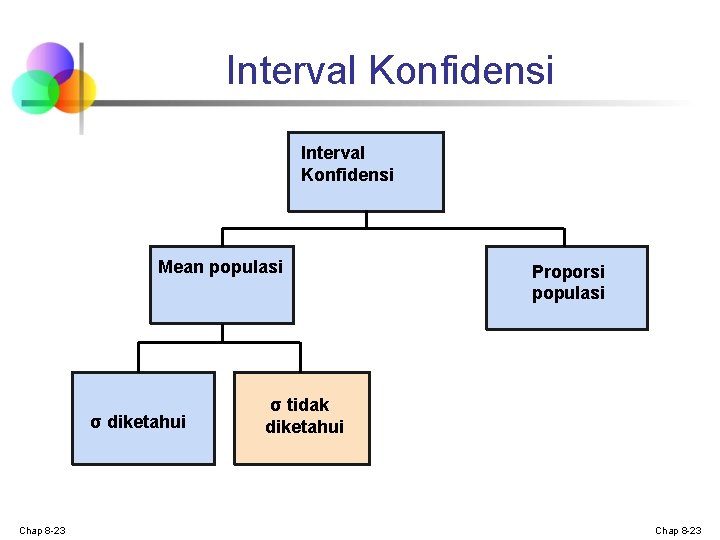
Interval Konfidensi Mean populasi σ diketahui Chap 8 -15 Proporsi populasi σ tidak diketahui Chap 8 -15

Interval Konfidensi bagi μ (σ diketahui) n n Asumsi-asumsi n Standar deviasi σ diketahui n Populasi berdistribusi normal n Jika populasi tidak normal, gunakan sampel besar (teori limit pusat) Estimasi interval konfidensi: where Zα/2 Chap 8 -16 estimasi titik kritis distribusi normal dengan probabilitas /2 standar error

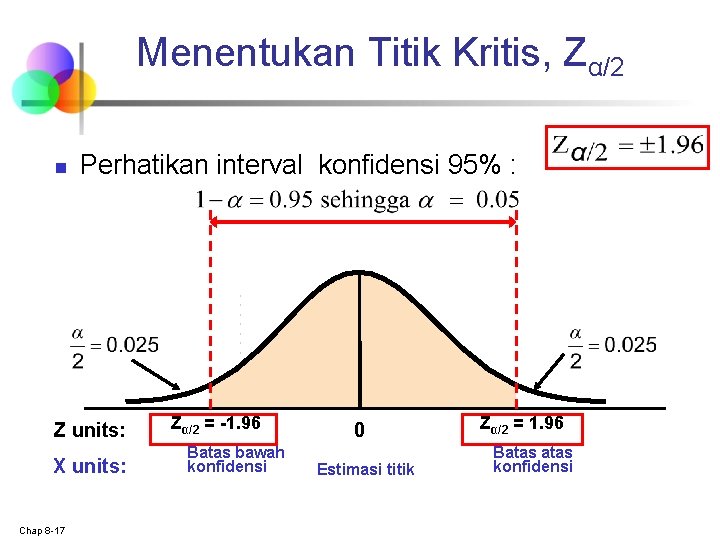
Menentukan Titik Kritis, Zα/2 n Perhatikan interval konfidensi 95% : Z units: X units: Chap 8 -17 Zα/2 = -1. 96 Batas bawah konfidensi 0 Estimasi titik Zα/2 = 1. 96 Batas konfidensi

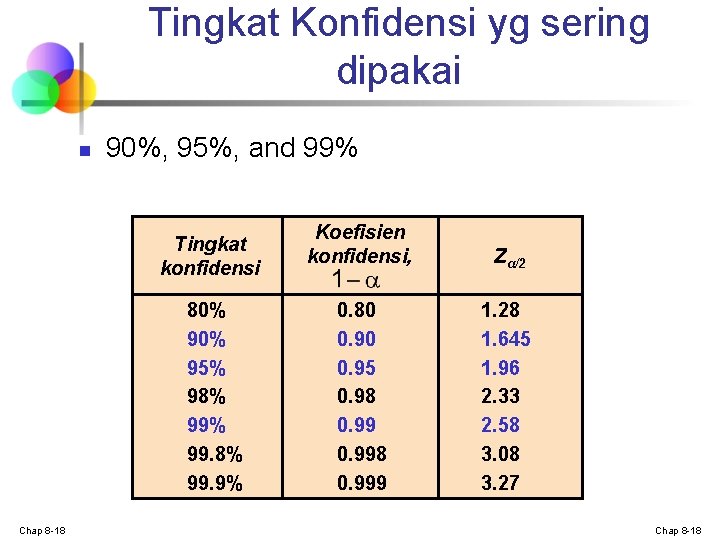
Tingkat Konfidensi yg sering dipakai n 90%, 95%, and 99% Tingkat konfidensi 80% 95% 98% 99. 9% Chap 8 -18 Koefisien konfidensi, Zα/2 0. 80 0. 95 0. 98 0. 998 0. 999 1. 28 1. 645 1. 96 2. 33 2. 58 3. 08 3. 27 Chap 8 -18

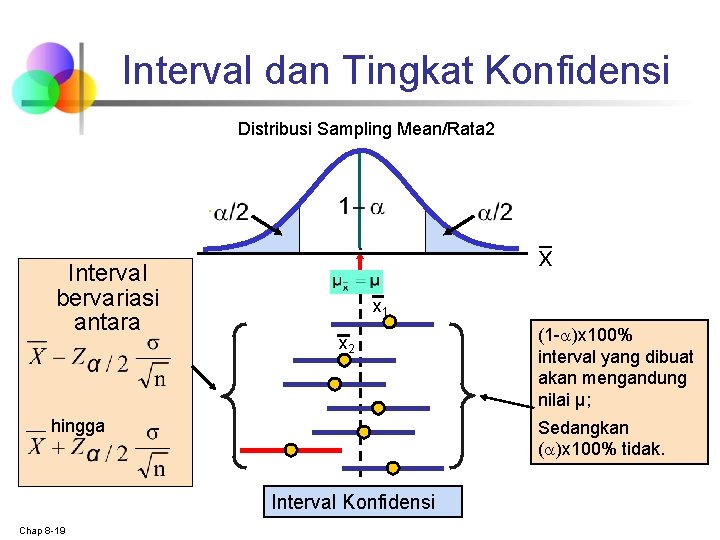
Interval dan Tingkat Konfidensi Distribusi Sampling Mean/Rata 2 Interval bervariasi antara x x 1 x 2 hingga Sedangkan ( )x 100% tidak. Interval Konfidensi Chap 8 -19 (1 - )x 100% interval yang dibuat akan mengandung nilai μ;

Contoh n Suatu penelitian tertarik untuk mengetahui rata 2 pendapatan manager pemasaran di industri retail. Suatu sampel yang terdiri atas 256 manager menunjukkan bahwa rata 2 pendapatan mereka adalah 454. 2 jt/th. Standar deviasi populasi ini adalah 20. 5 jt/th. Beberapa pertanyaan yg ingin dijawab dr penelitian tsb: n Berapa rata 2 populasi? Berapa kisaran nilai rata 2 populasi bila diinginkan tingkat konfidensi 95%? n Bagaimana menginterpretasi hasil tsb? n Chap 8 -20

Contoh n n Rata 2 populasi diestimasi sekitar 454. 2 jt/th (estimasi titik) Kisaran rata 2 populasi

n Interpretasi n n Chap 8 -22 Dengan tingkat keyakinan 95%, kita dapat menyatakan bahwa rata 2 sebenarnya dari pendapatan manager pemasaran di industri retail berkisar antara 451. 69 – 456. 71 jt/th. Mesikupun rata 2 sebenarnya boleh jadi tidak ada dalam interval ini, namun 95% interval konfidensi yang dibentuk dengan cara ini akan memuat nilai rata 2 populasi Chap 8 -22

Interval Konfidensi Mean populasi σ diketahui Chap 8 -23 Proporsi populasi σ tidak diketahui Chap 8 -23

Apakah standar deviasi populasi (σ) selalu diketahui? n Tentu saja tidak n Dalam dunia nyata, σ sangat jarang diketahui n n Chap 8 -24 Jika ada situasi dimana σ diketahui, maka µ juga pasti diketahui Jika µ diketahui, maka kita tidak perlu repot untuk mengumpulkan data sampel Copyright © 2012 Pearson Education, Inc. publishing as Chap 8 -24 Prentice Hall

Interval Konfidensi Bagi μ (σ tidak diketahui) DCOVA n n n Chap 8 -25 Jika standar deviasi populasi σ tidak diketahui, kita dapat menggantinya dengan standar deviasi sampel, S. Konsekuensinya, ketidakpastian menjadi meningkat, karena S bervariasi antar sampel Dengan demikian, digunakan distribusi-t bukan distribusi normal

Interval Konfidensi Bagi μ (σ tidak diketahui) n Interval konfidensi: (dimana tα/2, db adalah titik kritis distribusi t dengan derajat bebas (db) = n -1 dan luas area masing 2 α/2 di setiap sisi) Chap 8 -26

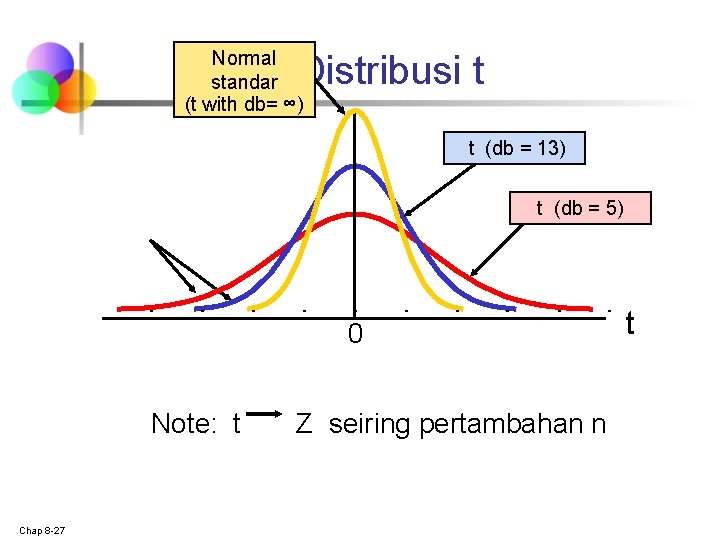
Normal standar (t with db= ∞) Distribusi t t (db = 13) t (db = 5) 0 Note: t Chap 8 -27 Z seiring pertambahan n t

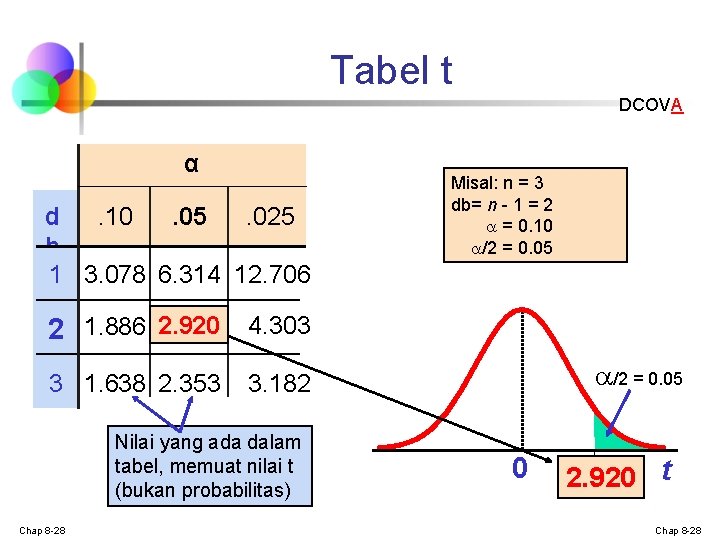
Tabel t DCOVA α d. 10. 05. 025 b 1 3. 078 6. 314 12. 706 Misal: n = 3 db= n - 1 = 2 = 0. 10 /2 = 0. 05 2 1. 886 2. 920 4. 303 3 1. 638 2. 353 Nilai yang ada dalam tabel, memuat nilai t (bukan probabilitas) Chap 8 -28 /2 = 0. 05 3. 182 0 2. 920 t Chap 8 -28

Contoh suatu sampel acak berukuran n = 25 memiliki X = 50 and S = 8. buatlah interval konfidensi 95% bagi for μ

Contoh suatu sampel acak berukuran n = 25 memiliki X = 50 and S = 8. buatlah interval konfidensi 95% bagi for μ n db = n – 1 = 24, sehingga Interval konfidensi 95% 46. 698 ≤ μ ≤ 53. 302 Chap 8 -30

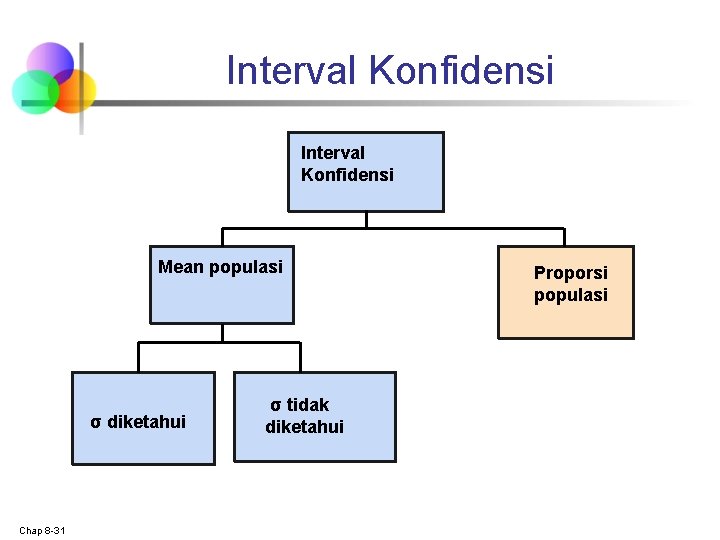
Interval Konfidensi Mean populasi σ diketahui Chap 8 -31 σ tidak diketahui Proporsi populasi

Interval Konfidensi Proporsi Populasi, π n n Chap 8 -32 Distribusi dari proprosi sampel akan mendekati normal jika ukuran sampel cukup besar, dengan standar deviasi Standar deviasi tersebut kemudian diestimasi dengan statistik sampel

Interval Konfidensi Proporsi Populasi, π n Interval konfidensi bagi π n Di mana n n Chap 8 -33 Zα/2 : nilai Z untuk tingkat konfidensi 1 -α p : proporsi sampel n : ukuran sampel Note: nilai X harus memenuhi X > 5 dan n – X > 5

Contoh n n Chap 8 -34 Suatu sampel acak berukuran 100 orang menunjukkan bahwa 25 diantaranya kidal. Buat interval konfidensi 95% untuk proporsi sebenarnya anggota populasi yang kidal. Chap 8 -34

Contoh n Suatu sampel acak berukuran 100 orang menunjukkan bahwa 25 diantaranya kidal. Buat interval konfidensi 95% untuk proporsi sebenarnya anggota populasi yang kidal. np = 100 * 0. 25 = 25 > 5 & n(1 -p) = 100 * 0. 75 = 75 > 5 Pastikan ukuran Sampel cukup besar Chap 8 -35

TUGAS 1. Sebuah lembaga penelitian tertarik untuk mengetahui pengeluaran untuk rokok selama seminggu dari para perokok aktif. Sampel acak berukuran 49 orang perokok aktif dipilih dengan rata 2 pengeluaran untuk rokok sebesar 200 ribu/minggu. Dari penelitian sebelumnya diketahui standar deviasi populasi ini adalah 50 rb/minggu. Buatlah interval konfidensi 95% bagi rata 2 sebenarnya pengeluaran untuk rokok para perokok aktif ini dan interpretasikan.

2. Asosiasi industri pertanian bertujuan untuk mengetahui rata 2 konsumsi susu tahunan. Untuk itu dipilih 16 orang secara acak, di mana rata 2 konsumsi susu tahunan ke-16 orang tsb adalah 60 gallon dan standar deviasi 20 gallon. Buatlah interval konfidensi 90% bagi rata 2 populasi dan interpretasikan.

3. Pemilik Minimarket Sardo tertarik untuk mengetahui proporsi pelanggan yg menggunakan kartu kredit/debit untuk pembayaran. Dia melakukan survey thdp 100 pelanggan dan menemukan 20 diantaranya menggunakan kartu kredit/debit. Buatlah interval konfidensi 95% bagi proporsi populasi dan interpretasikan.