Statistik Deskriptif Oleh Abdi Santoso Mustafa DS Mara

Statistik Deskriptif Oleh : Abdi Santoso Mustafa DS Mara Imam Taufik Siregar T. Kemala Intan 1

Defenisi Statistika deskriptif (descriptive statistics) berkaitan dengan penerapan metode statistik untuk mengumpulkan, mengolah, menyajikan dan menganalisis data kuantitatif secara deskriptif � Analisa data diawali dengan analisa sederhana analisa yang lebih kompleks sesuai dengan tujuan penelitian (bila perlu) � Analisa sederhana : ukuran nilai tengah dan dispersi � Analisa Kompleks : rata-rata dan standar deviasi � 2

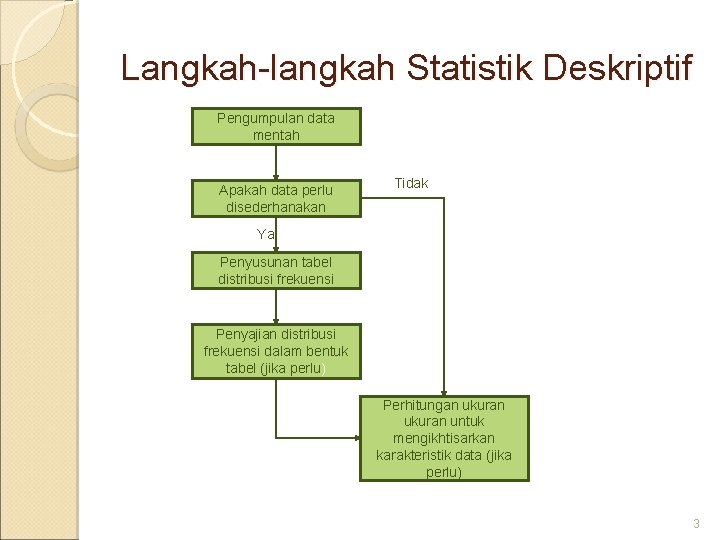
Langkah-langkah Statistik Deskriptif Pengumpulan data mentah Apakah data perlu disederhanakan Tidak Ya Penyusunan tabel distribusi frekuensi Penyajian distribusi frekuensi dalam bentuk tabel (jika perlu) Perhitungan ukuran untuk mengikhtisarkan karakteristik data (jika perlu) 3

Ukuran Nilai Tengah � Yaitu suatu nilai yang dapat mewakili sekelompok nilai hasil pengamatan disebut juga nilai rata � Macam-macam nilai tengah : 1. Rata-rata hitung (arithmatic mean), disingkat mean 2. Rata-rata ukur (geometrik mean) 3. Median, dan 4. Modus (mode) 4

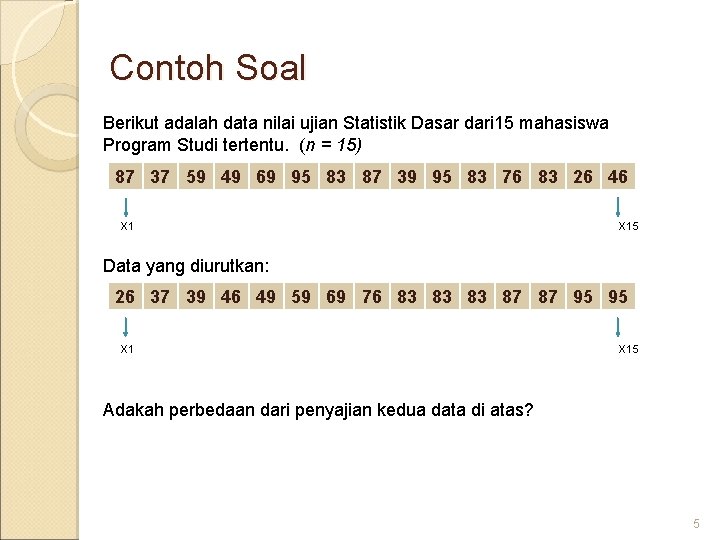
Contoh Soal Berikut adalah data nilai ujian Statistik Dasar dari 15 mahasiswa Program Studi tertentu. (n = 15) 87 37 59 49 69 95 83 87 39 95 83 76 83 26 46 X 15 Data yang diurutkan: 26 37 39 46 49 59 69 76 83 83 83 87 87 95 95 X 15 Adakah perbedaan dari penyajian kedua data di atas? 5

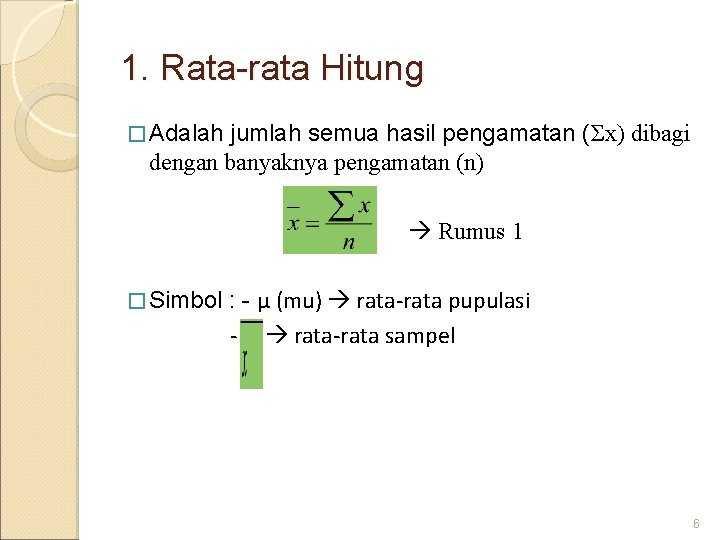
1. Rata-rata Hitung � Adalah jumlah semua hasil pengamatan (Σx) dibagi dengan banyaknya pengamatan (n) Rumus 1 � Simbol : - μ (mu) rata-rata pupulasi - rata-rata sampel 6

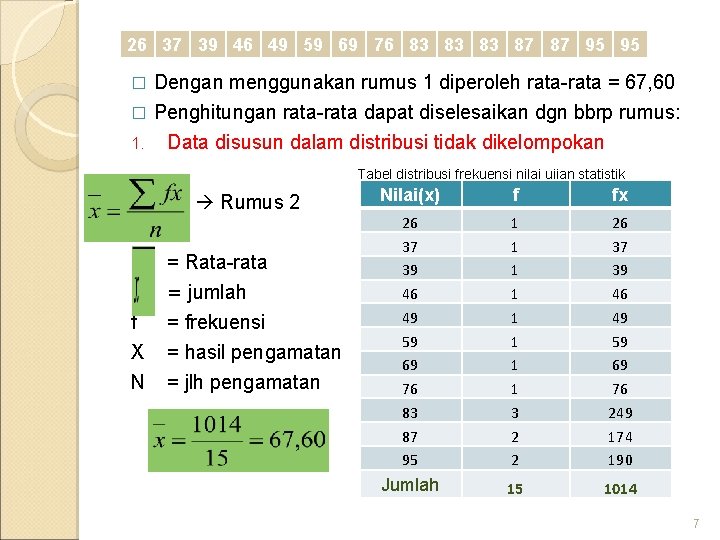
26 37 39 46 49 59 69 76 83 83 83 87 87 95 95 Dengan menggunakan rumus 1 diperoleh rata-rata = 67, 60 � Penghitungan rata-rata dapat diselesaikan dgn bbrp rumus: � 1. Data disusun dalam distribusi tidak dikelompokan Tabel distribusi frekuensi nilai ujian statistik 1. Rumus 2 ∑ = Rata-rata = jumlah f X N = frekuensi = hasil pengamatan = jlh pengamatan Nilai(x) f fx 26 37 39 46 49 59 69 76 83 87 95 1 1 1 1 3 2 2 26 37 39 46 49 59 69 76 249 174 190 Jumlah 15 1014 7

2. Data disusun dalam distribusi frekuensi dikelompokan pada interval kelas yang sama Tabel distribusi frekuensi dikelompokan Rumus 3 = rata-rata Σ = Jumlah f = frekuensi Nt= Nilai tengah Interval f Nt f. Nt 11 -30 1 20. 5 31 -40 2 35. 5 71 41 -50 2 45. 5 91 51 -60 1 55. 5 61 -70 1 65. 5 71 -80 1 75. 5 81 -90 5 85. 5 427. 5 91 -110 2 105 201 Jumlah 15 1007. 5 8

3. Perhitungan rata-rata menggunakan kode Rumus 4 kode Nt 0 i f d n = Rata-rata = nilai tengah ttk nol = interval kelas = Frekuensi = kode = jumlah pengamatan Tabel distribusi frekuensi Interval f Nt d fd 21 -30 1 25. 5 -2 -2 31 -40 2 35. 5 -1 -2 41 -50 2 45. 5 0 0 51 -60 1 55. 5 1 1 61 -70 1 65. 5 2 2 71 -80 1 75. 5 3 3 81 -90 5 85. 5 4 20 91 -100 2 95. 5 5 10 Jumlah 15 32 9

4. Distribusi frekuensi dengan interval kelas tidak sama Rumus 4 Tabel distribusi frekuensi interval tidak sama Nt 0 i f d n = Rata-rata = nilai tengah ttk nol = interval kelas = Frekuensi = kode = jumlah pengamatan Rumus 5 interval f Nt d fd 21 -30 1 25. 5 -3 -3 31 -40 2 35. 5 -2 -4 41 -50 2 45. 5 -1 -2 51 -60 1 55. 5 0 0 61 -70 1 65. 5 1 1 71 -80 1 75. 5 2 2 81 -90 5 85. 5 3 15 91 -100 2 95. 5 4 8 Jumlah 15 17 i = 10 10

2. Rata-rata ukur (Geometric mean) � Adalah akar pangkat n dari hasil perkalian setiap pengamatan Rumus 6 Cth. Lama pengobatan thdp 3 org, yaitu 3, 9 dan 27 hari � Bila n besar, gunakan logaritmanya Rumus 7 11

� Dengan rumus 7, diperoleh hasil Log 3 = 0, 4771 Log 9 = 0, 9642 Log 27 = 1, 4313 12

3. Median � Merupakan ukuran nilai tengah yang berada dengan rata-rata (mean) karena median hanya menyatakan posisi tengah dari sederetan angka. � Membagi dua sama banyak, 50% berada dibawah median dan 50% diatas median Rumus 8 Me = Median n = Banyaknya pengamatan 13

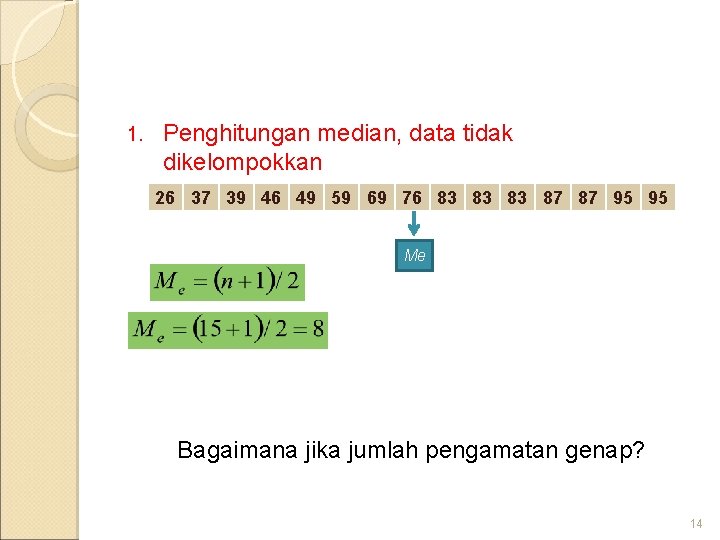
1. Penghitungan median, data tidak dikelompokkan 26 37 39 46 49 59 69 76 83 83 83 87 87 95 95 Me Bagaimana jika jumlah pengamatan genap? 14

2. Penghitungan median pada distribusi frekuensi yang dikelompokan Rumus 9 Me = median Me’ = nilai sebelum median tercapai i = interval kelas Me” = posisi median = ½ n fkum = frekuensi kumulatif dari tepi bawah kelas sebelum median f = frekuensi kelas dimana median berada 15

26 37 39 46 49 59 69 76 83 83 83 87 87 95 95 � Jumlah pengamatan dari median = ½n = 7, 5 Median terletak pada posisi 7 dan 8 � Nilai median sebelum tercapai 60 � Interval kelas 10 � Frekuensi kumulatif kelas sblm median = 6 � Frekuensi kelas dimana median berada = 1 Me Interval f Fkum < batas 21 -30 1 1 31 -40 2 3 41 -50 2 5 51 -60 1 6 61 -70 1 7 71 -80 1 8 81 -90 5 13 91 -100 2 15 Jumlah 15 � 16

Perhitungan diatas dapat dijelaskan sbb: Frek. tepi kelas -/------/-----/-----/----/ 20 30 40 50 60 70 80 90 100 f. kum<tepi atas 0 1 3 5 6 7 8 13 15 Jumlah pengamatan dari median = ½ n = 7, 5 Nilai statistik 70 terdapat hanya 7 pengamatan Nilai statistik 80 terdapat hanya 8 pengamatan Jadi, median terletak antara 70 dan 80 Penambahan ½ x 10 = 5 Median = 70 + 5 = 75 17

Modus Merupakan salah satu ukuran nilai tengah yang dinyatakan dalam frekuensi terbanyak dari data kumulatif maupun data kuantitatif � Modus bisa juga dinyatakan sebagai puncak suatu kurva, dikenal unibola satu puncak, bimodal dua puncak, mutimodal lebih dari dua � Perhitungan modus dapat dilakukan: 1. Untuk data distribusi frekuensi yang tidak dikelompokan 2. Untuk data distribusi frekuensi yang dikelompokan � 18

Perhitungan modus untuk data yang tidak dikelompokan 26 37 39 46 49 59 69 76 83 83 83 87 87 95 95 Mod Perhitungan modus untuk data distribusi frekuensi dikelompokan Rumus 10 Mo = Modus Lmo = tepi bawah kelas dimana modus berada d 1 = selisih antara frekuensi kelas modus dengan kelas tepat dibawahnya d 2 = selisih antara frekuensi kelas modus dengan kelas tepat diatasnya i = interval 19

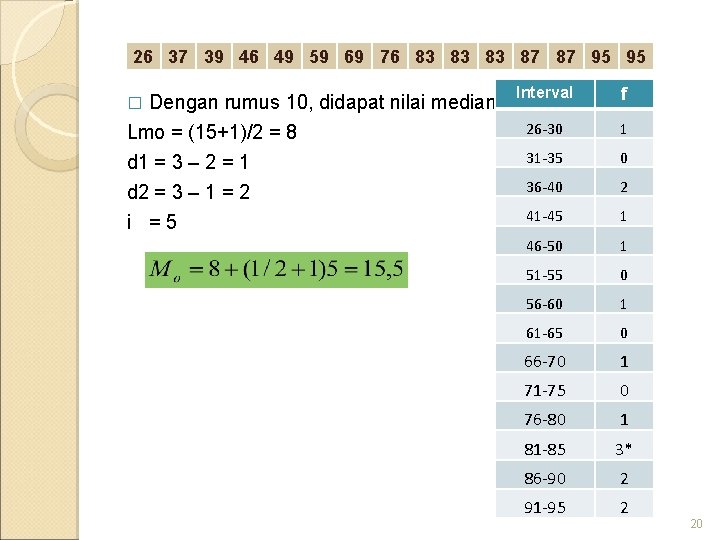
26 37 39 46 49 59 69 76 83 83 83 87 87 95 95 Dengan rumus 10, didapat nilai median Lmo = (15+1)/2 = 8 d 1 = 3 – 2 = 1 d 2 = 3 – 1 = 2 i =5 � Interval f 26 -30 1 31 -35 0 36 -40 2 41 -45 1 46 -50 1 51 -55 0 56 -60 1 61 -65 0 66 -70 1 71 -75 0 76 -80 1 81 -85 3* 86 -90 2 91 -95 2 20

Dispersi (Ukuran Penyimpangan=Ukuran Variasi) � Dipersi 1. 2. 3. digunakan untuk : Mendapatkan informasi tambahan tentang penyimpangan yang terjadi pada suatu distribusi Kita dapat menilai ketepatan nilai tengah dalam mewakili distribusinya. Perhitungan dispersi juga mempunyai arti penting untuk mengadakan analisis melalui perhitungan statistik yang lebih mendalam 21

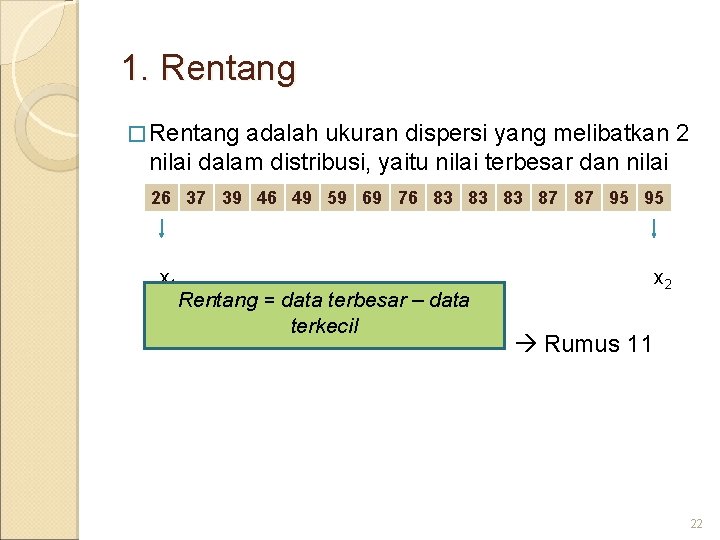
1. Rentang � Rentang adalah ukuran dispersi yang melibatkan 2 nilai dalam distribusi, yaitu nilai terbesar dan nilai terkecil 26 37 39 46 49 59 69 76 83 83 83 87 87 95 95 x 1 Rentang = data terbesar – data terkecil x 2 Rumus 11 22

2. Quartil 26 37 39 46 49 59 69 76 83 83 83 87 87 95 95 q 1 q 2 = med q 3 23

3. Rentang Antar-Quartil (Jangkauan Antar Kuartil) � Adalah selisih antara q 3 dengan q 1 yang sama dengan 50% bagian tengah dari seluruh distribusi. � Deviasi quartil Rumus 12 � Median ]] Rumus 13 24

4. Decil (Decile) � Data yang telah disusun menjadi distribusi dan dibagi menjadi 10 bagian yang sama. � Rumus 14 25

5. Persentil (persentil) � Adalah suatu distribusi dibagi menjadi 100 bagian yang sama, dengan cara demikian kita mendapatkan 99 bagian yang sama. Rumus 15 26

Jumlah dan Interval Kelompok � Menentukan banyaknya kelompok (Sturges-1926) Rumus 16 m = Jumlah kelompok 26 37 39 46 49 59 69 76 83 83 83 87 87 95 95 � Menentukan interval kelompok Rumus 17 R = Rentang Maka data tersebut mempunyai 5 kelompok dengan interval 14 27

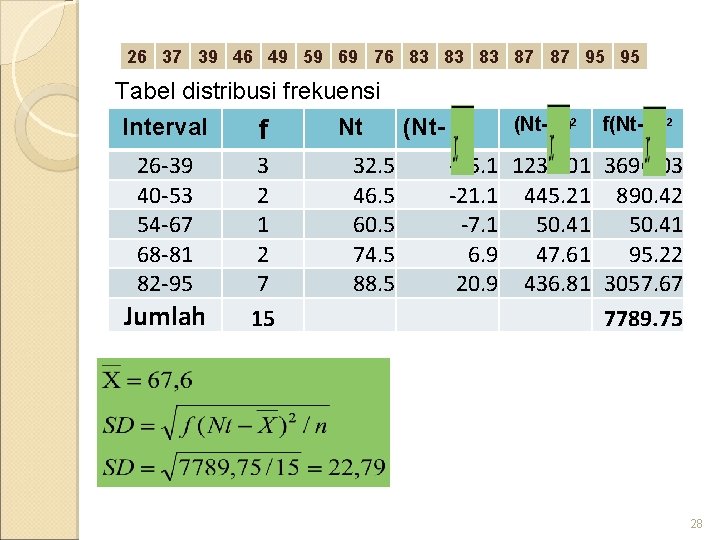
26 37 39 46 49 59 69 76 83 83 83 87 87 95 95 Tabel distribusi frekuensi Interval Nt (Nt- ) f 26 -39 40 -53 54 -67 68 -81 82 -95 Jumlah 3 2 1 2 7 15 32. 5 46. 5 60. 5 74. 5 88. 5 (Nt- )2 f(Nt- )2 -35. 1 1232. 01 3696. 03 -21. 1 445. 21 890. 42 -7. 1 50. 41 6. 9 47. 61 95. 22 20. 9 436. 81 3057. 67 7789. 75 28

26 37 39 46 49 59 69 76 83 83 83 87 87 95 95 � Untuk data tidak dikelompokan 29

Koevesien Variasi � Untuk data dikelompokan � Untuk data tidak dikelompokan 30

JAWABAN TUGAS 31

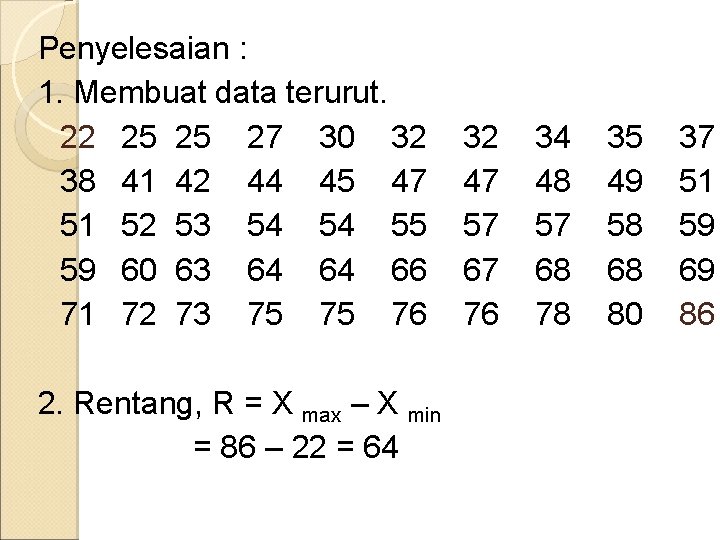
Penyelesaian : 1. Membuat data terurut. 22 25 25 27 30 32 38 41 42 44 45 47 51 52 53 54 54 55 59 60 63 64 64 66 71 72 73 75 75 76 2. Rentang, R = X max – X min = 86 – 22 = 64 32 47 57 67 76 34 48 57 68 78 35 49 58 68 80 37 51 59 69 86

3. Banyaknya kelas dengan rumus STURGES : k = 1 + 3, 3 log N k = 1 + 3, 3 log 50 k = 6, 6 7 4. Interval Kelas : I = R / k = 64 / 7 = 9, 14 10

6. Titik tengah kelas ke-1 = ½ (29 + 20) = 49/2 = 24, 5 7. Memasukkan data ke dalam kelas yang sesuai, dengan memakai sistem Tally/Turus.

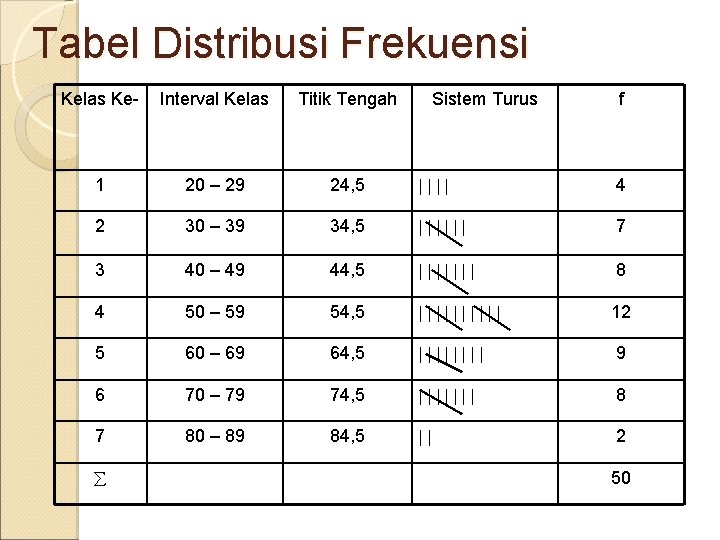
Tabel Distribusi Frekuensi Kelas Ke- Interval Kelas Titik Tengah 1 20 – 29 24, 5 4 2 30 – 39 34, 5 7 3 40 – 49 44, 5 8 4 50 – 59 54, 5 12 5 60 – 69 64, 5 9 6 70 – 79 74, 5 8 7 80 – 89 84, 5 2 Sistem Turus f 50

DISTRIBUSI FREKUENSI RELATIF Interval Kelas Frekuensi Relatif (%) 20 – 29 4 4/50 x 100% = 8% 30 – 39 7 14 40 – 49 8 16 50 – 59 12 24 60 – 69 9 18 70 – 79 8 16 80 – 89 2 4 50 100

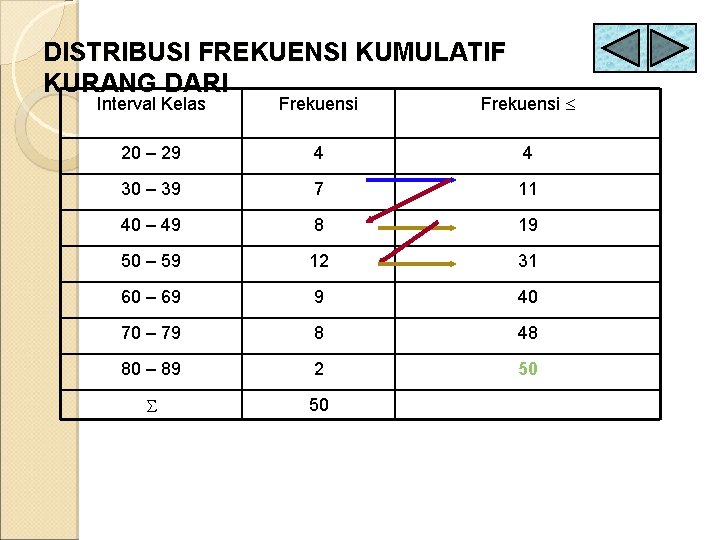
DISTRIBUSI FREKUENSI KUMULATIF KURANG DARI Interval Kelas Frekuensi 20 – 29 4 4 30 – 39 7 11 40 – 49 8 19 50 – 59 12 31 60 – 69 9 40 70 – 79 8 48 80 – 89 2 50 50

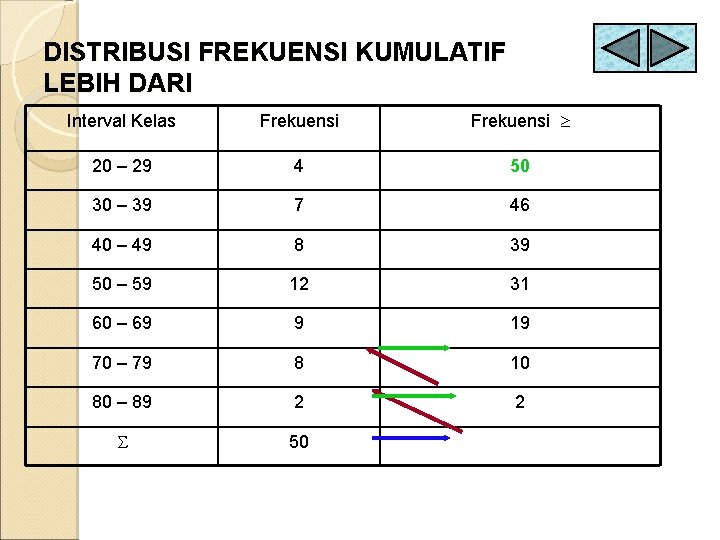
DISTRIBUSI FREKUENSI KUMULATIF LEBIH DARI Interval Kelas Frekuensi 20 – 29 4 50 30 – 39 7 46 40 – 49 8 39 50 – 59 12 31 60 – 69 9 19 70 – 79 8 10 80 – 89 2 2 50

DISTRIBUSI FREKUENSI KUMULATIF RELATIF KURANG DARI Interval Kelas Frekuensi Kumulatif Relatif (%) < 19, 5 0 0/50 x 100% = 0 % < 29, 5 4 4/50 x 100% = 8 % < 39, 5 11 22 < 49, 5 19 38 < 59, 5 31 62 < 69, 5 40 80 < 79, 5 48 96 < 89, 5 50 100