STATISTIK 1 Pertemuan 11 Deret Berkala dan Peramalan

STATISTIK 1 Pertemuan 11: Deret Berkala dan Peramalan (Analisis Trend) Dosen Pengampu MK: Evellin Lusiana, S. Si, M. Si

Materi Hari Ini n Pendahuluan n Metode analisis trend n n Metode semi rata-rata Metode kuadrat terkecil Metode tren kuadratis Metode tren eksponensial

Pendahuluan [1] n Deret berkala – Time series n n Sekumpulan data yang dicatat dalam satu periode waktu Digunakan untuk meramalkan kondisi masa mendatang Dalam jangka pendek (kurang dari 1 tahun ) atau jangka panjang (lebih dari 3 tahun) Berguna untuk penyusunan recana (perusahaan dan negara)

Pendahuluan [2] n Deret berkala mempunyai empat komponen : n n Tren – kecenderungan (T) Variasi musim (S) Variasi siklus (C) Variasi yang tidak tetap – irregular variation (I) Deret Berkala Biasa Dinyatakan Y=Tx. Sx. Cx. I

Tren - Kecenderungan n n Tren n Merupakan suatu gerakan kecenderungan naik atau turun dalam jangka panjang yang diperoleh dari rata-rata perubahan dari waktu ke waktu dan nilainya cukup rata atau mulus Bentuk tren n Tren positif = tren meningkat Y = a + b. X n Tren negatif = tren menurun Y = a – b. X

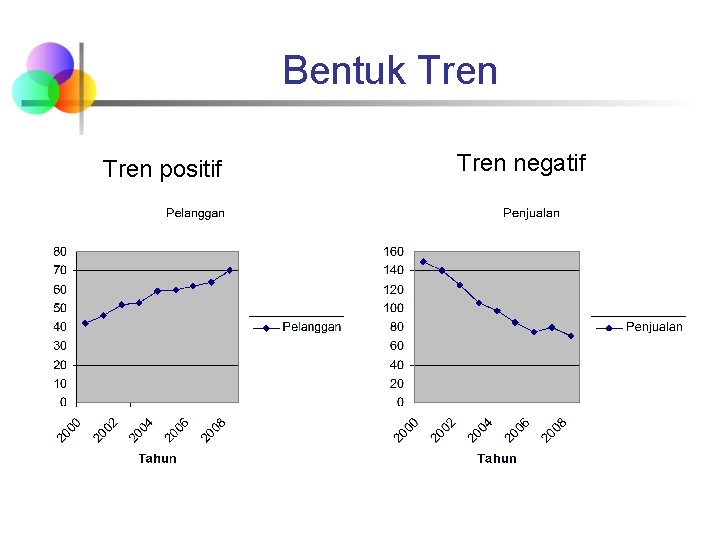
Bentuk Tren positif Tren negatif

Metode Analisa Tren n n Metode semi rata – rata ( Semi average method) Metode kuadrat terkecil ( Least square method) Metode tren kuadratis ( Quadratic trend method) Metode tren eksponensial ( Exponential trend method)

Metode Semi Rata - rata n n Dengan cara mencari rata – rata kelompok data Langkah : n n n Kelompokan data menjadi dua kelompok Hitung rata – rata hitung dan letakkan di tengah kelompok ( K 1 dan K 2). Nilai yang dihasilkan menjadi nilai konstanta (a) dan letak tahun merupakan tahun dasar Hitung selisih K 2 – K 1 n n K 2 – K 1 > 0 = Tren positif K 2 – K 1 < 0 = Tren negatif

Tentukan nilai perubah tren (b) dengan cara : K 2 – K 1 b = th dasar 2 – th dasar 1 n n n Persamaan tren ; Y’ = a + b. X Untuk mengetahui besarnya tren, masukan nilai (X) pada persamaan Untuk data ganjil, data (tahun) tengah dapat dihilangkan atau dihitung dua kali

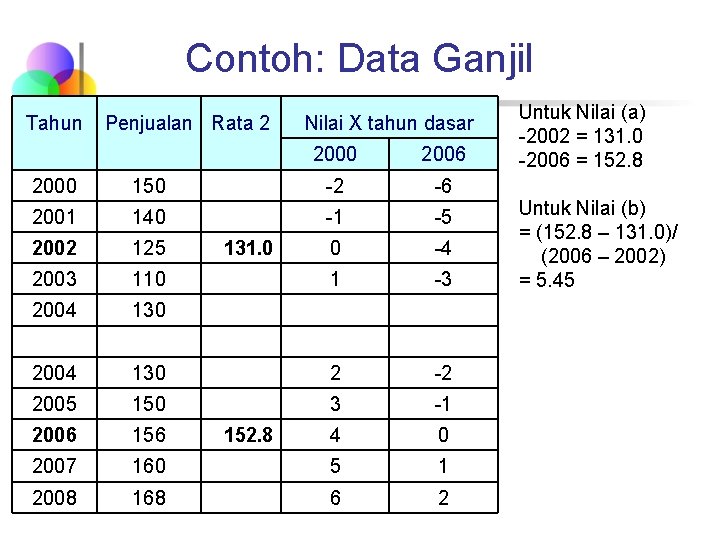
Contoh: Data Ganjil Tahun Penjualan Rata 2 2000 150 2001 140 2002 125 2003 110 2004 Nilai X tahun dasar 2000 2006 -2 -6 -1 -5 0 -4 1 -3 130 2004 130 2 -2 2005 150 3 -1 2006 156 4 0 2007 160 5 1 2008 168 6 2 131. 0 152. 8 Untuk Nilai (a) -2002 = 131. 0 -2006 = 152. 8 Untuk Nilai (b) = (152. 8 – 131. 0)/ (2006 – 2002) = 5. 45

n Maka persamaan tren n Tahun dasar 2002 Y’ = 131+ 5. 45 X) Tahun dasar 2006 Y’ = 152. 8 + 5. 45 (X) Peramalan tahun 2009 n n Y’ 2002 = 131+ 5. 45 (7) = 169. 15 Y’ 2006= 152. 8 + 5. 45 (3) = 169. 15

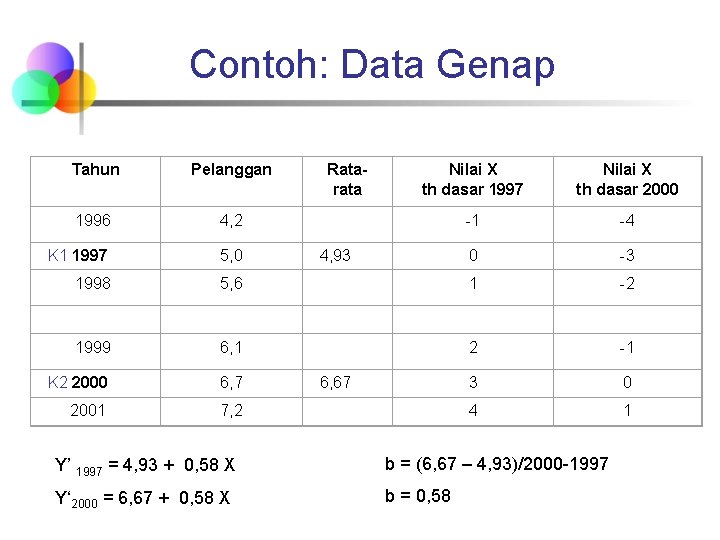
Contoh: Data Genap Tahun Pelanggan Ratarata Nilai X th dasar 1997 Nilai X th dasar 2000 1996 4, 2 -1 -4 K 1 1997 5, 0 4, 93 0 -3 1998 5, 6 1 -2 1999 6, 1 2 -1 K 2 2000 6, 7 6, 67 3 0 2001 7, 2 4 1 Y’ 1997 = 4, 93 + 0, 58 X b = (6, 67 – 4, 93)/2000 -1997 Y‘ 2000 = 6, 67 + 0, 58 X b = 0, 58

Metode Kuadrat Terkecil (OLS) n n n Dengan menentukan garis tren yang mempunyai jumlah terkecil dari kuadrat selisih data asli dengan data pada garis tren Persamaan ; Y’ = a + b. X Mencari nilai koefisien - utk tahun ganjil, koding X =. . . . -3, -2, -1, 0, 1, 2, 3, . . - utk tahun genap, koding X= . . . . -5, - 3, -1, 1 , 3, 5, . .

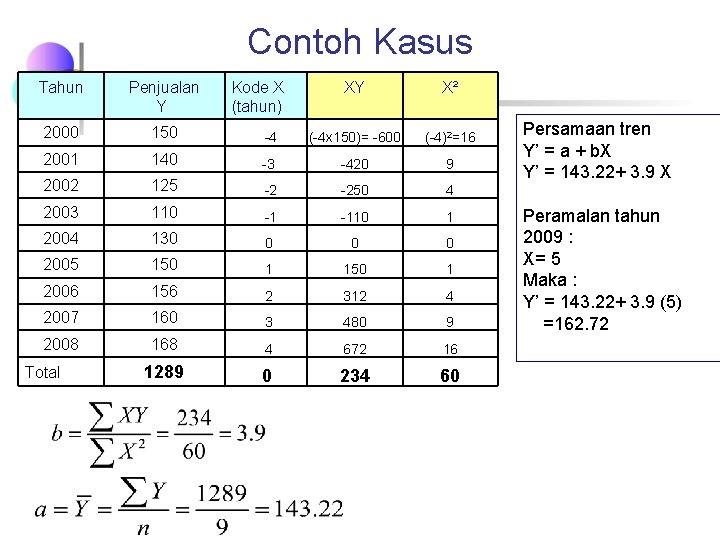
Contoh Kasus Tahun Penjualan Y 2000 150 2001 XY X² -4 (-4 x 150)= -600 (-4)2=16 140 -3 -420 9 2002 125 -2 -250 4 2003 110 -1 -110 1 2004 130 0 2005 150 1 2006 156 2 312 4 2007 160 3 480 9 2008 168 4 672 16 1289 0 234 60 Total Kode X (tahun) Persamaan tren Y’ = a + b. X Y’ = 143. 22+ 3. 9 X Peramalan tahun 2009 : X= 5 Maka : Y’ = 143. 22+ 3. 9 (5) =162. 72

Metode Tren Kuadratis n n n Digunakan untuk tren jangka panjang yang polanya tidak linier Maka digunakan metode tren kuadratis, persamaan : Y = a + b. X + c. X 2 Nilai koefisien :

Metode Tren Kuadratis n Nilai koefisien :

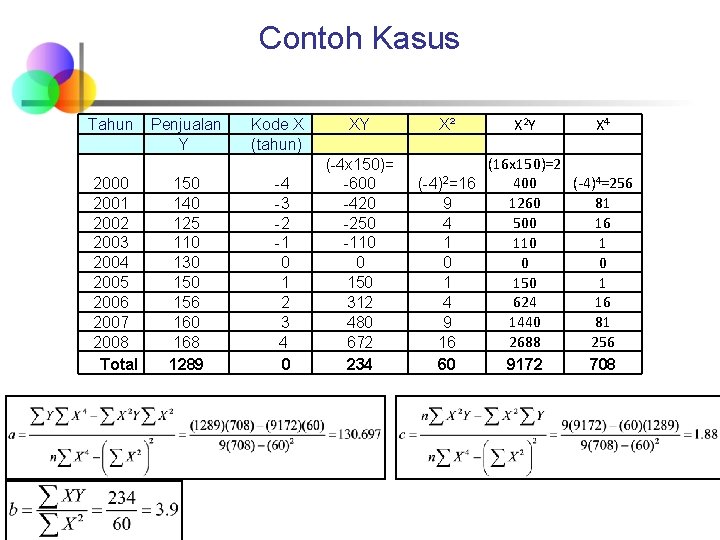
Contoh Kasus Tahun 2000 2001 2002 2003 2004 2005 2006 2007 2008 Total Penjualan Y 150 140 125 110 130 156 160 168 1289 Kode X (tahun) -4 -3 -2 -1 0 1 2 3 4 0 X 2 Y X 4 XY X² (16 x 150)=2 (-4 x 150)= 400 (-4)4=256 -600 (-4)2=16 1260 81 -420 9 500 16 -250 4 110 1 -110 1 0 0 150 1 624 16 312 4 1440 81 480 9 2688 256 672 16 234 60 9172 708

Persamaan tren kuadratis Y’ = 130. 697 + 3. 9 X + 1. 88 X 2 n Jadi Peramalan penjualan untuk tahun 2009 (X = 4) adalah : Y’ = 130. 697 + 3. 9(5) + 1. 88(5)2 Y’=197. 17 n

Metode tren eksponensial n n n Suatu tren yang mempunyai pangkat atau eksponen dari waktu Bentuk persamaan : Y = a(1 + b)x Koefisien :

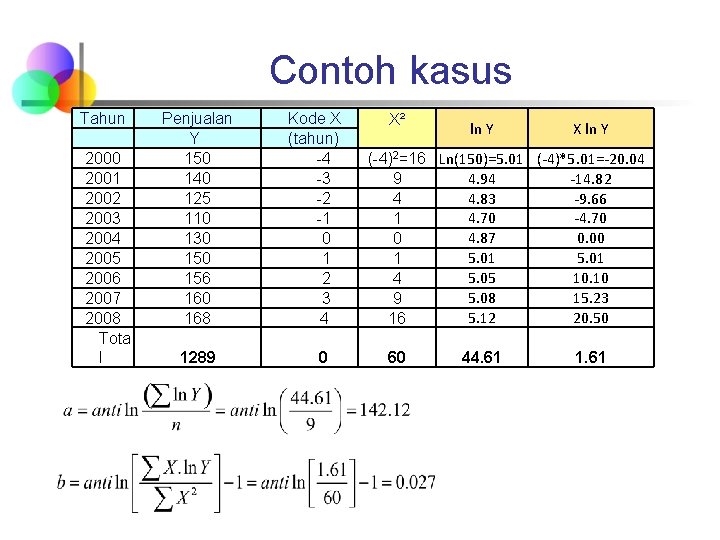
Contoh kasus Tahun 2000 2001 2002 2003 2004 2005 2006 2007 2008 Tota l Penjualan Y 150 140 125 110 130 156 160 168 1289 Kode X (tahun) -4 -3 -2 -1 0 1 2 3 4 0 X² ln Y X ln Y (-4)2=16 Ln(150)=5. 01 (-4)*5. 01=-20. 04 4. 94 -14. 82 9 4. 83 -9. 66 4 4. 70 -4. 70 1 4. 87 0. 00 0 5. 01 1 5. 05 10. 10 4 5. 08 15. 23 9 5. 12 20. 50 16 60 44. 61 1. 61

Persamaan tren eksponensial Y’ = a(1 + b)x Y’ = 142. 12 (1 + 0. 027)x n Peramalan penjualan tahun 2009 ( X =5 ), sebesar : Y’ = 142. 12 (1 + 0. 027)5 Y’= 162. 37 n

Memilih Persamaan Tren Terbaik n n n Dalam memilih metode tren yang terbaik dapat digunakan ukuran ketepatan Ukuran ketepatan adalah seberapa tepat sebuah alat peramalan tersebut menduga kejadian yang sebenarnya Kriteria yang digunakan yaitu ∑(Y – Y’)2 paling kecil

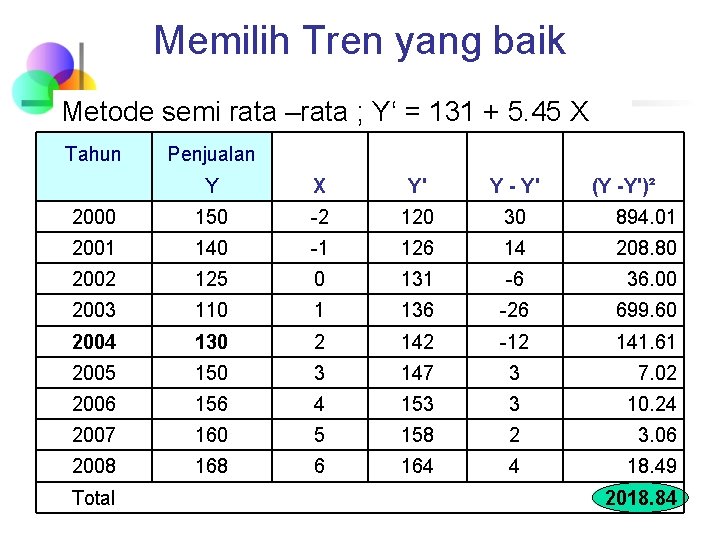
Memilih Tren yang baik Metode semi rata –rata ; Y‘ = 131 + 5. 45 X Tahun Penjualan Y X Y' Y - Y' 2000 150 -2 120 30 894. 01 2001 140 -1 126 14 208. 80 2002 125 0 131 -6 36. 00 2003 110 1 136 -26 699. 60 2004 130 2 142 -12 141. 61 2005 150 3 147 3 7. 02 2006 156 4 153 3 10. 24 2007 160 5 158 2 3. 06 2008 168 6 164 4 18. 49 Total (Y -Y')² 2018. 84

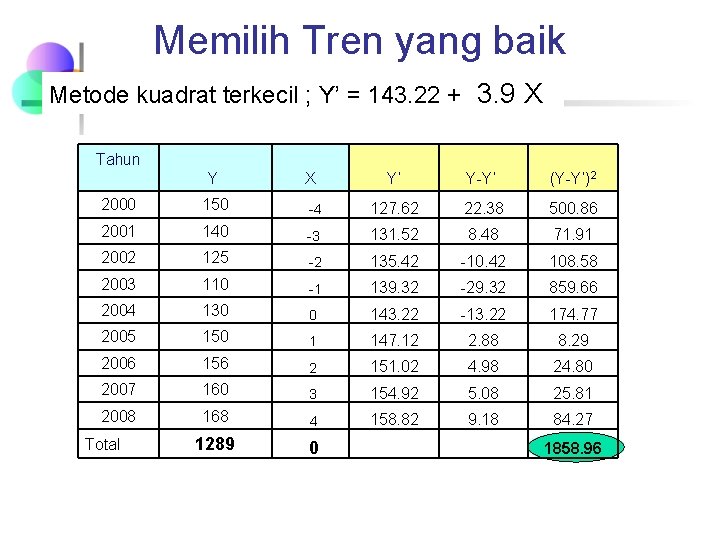
Memilih Tren yang baik Metode kuadrat terkecil ; Y’ = 143. 22 + 3. 9 X Tahun Y 2000 150 2001 Y’ Y-Y’ (Y-Y’)2 -4 127. 62 22. 38 500. 86 140 -3 131. 52 8. 48 71. 91 2002 125 -2 135. 42 -10. 42 108. 58 2003 110 -1 139. 32 -29. 32 859. 66 2004 130 0 143. 22 -13. 22 174. 77 2005 150 1 147. 12 2. 88 8. 29 2006 156 2 151. 02 4. 98 24. 80 2007 160 3 154. 92 5. 08 25. 81 2008 168 4 158. 82 9. 18 84. 27 1289 0 Total X 1858. 96

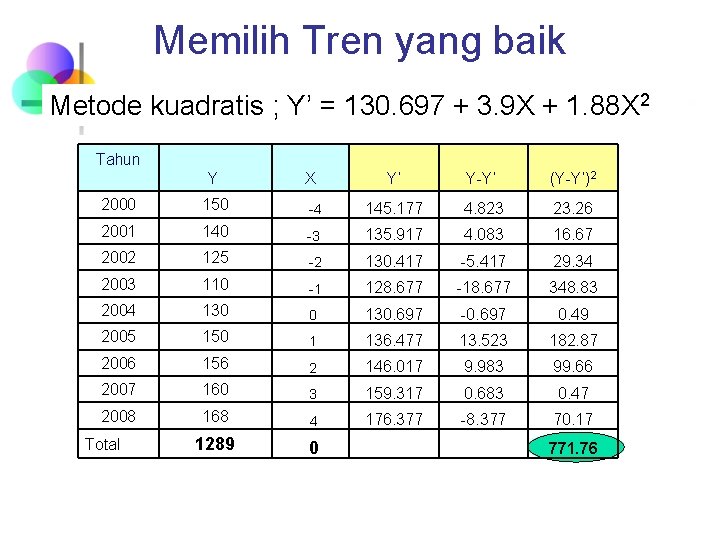
Memilih Tren yang baik Metode kuadratis ; Y’ = 130. 697 + 3. 9 X + 1. 88 X 2 Tahun Y 2000 150 2001 Y’ Y-Y’ (Y-Y’)2 -4 145. 177 4. 823 23. 26 140 -3 135. 917 4. 083 16. 67 2002 125 -2 130. 417 -5. 417 29. 34 2003 110 -1 128. 677 -18. 677 348. 83 2004 130 0 130. 697 -0. 697 0. 49 2005 150 1 136. 477 13. 523 182. 87 2006 156 2 146. 017 9. 983 99. 66 2007 160 3 159. 317 0. 683 0. 47 2008 168 4 176. 377 -8. 377 70. 17 1289 0 Total X 771. 76

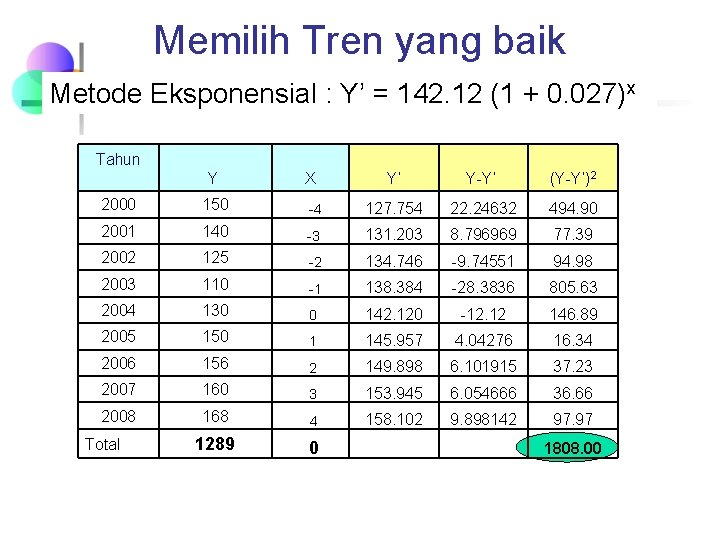
Memilih Tren yang baik Metode Eksponensial : Y’ = 142. 12 (1 + 0. 027)x Tahun Y 2000 150 2001 Y’ Y-Y’ (Y-Y’)2 -4 127. 754 22. 24632 494. 90 140 -3 131. 203 8. 796969 77. 39 2002 125 -2 134. 746 -9. 74551 94. 98 2003 110 -1 138. 384 -28. 3836 805. 63 2004 130 0 142. 120 -12. 12 146. 89 2005 150 1 145. 957 4. 04276 16. 34 2006 156 2 149. 898 6. 101915 37. 23 2007 160 3 153. 945 6. 054666 36. 66 2008 168 4 158. 102 9. 898142 97. 97 1289 0 Total X 1808. 00

Memilih Tren yang baik n Kesimpulan : n n Tren semi rata – rata Tren Kuadrat terkecil Tren kuadratis Tren Eksponensial : 2018. 84 : 1858. 96 : 771. 76 : 1808. 00 Metode kuadratis yang lebih kecil, Jadi metode yang cocok untuk meramalkan penjualan adalah metode kuadratis