Statistics Workshop ISRU Contents Data Types Descriptive Statistics

Statistics Workshop ISRU

Contents • Data Types & Descriptive Statistics • Confidence Intervals • Hypothesis Testing • Two Sample Tests • Further Hypothesis Testing (inc. ANOVA & Regression)

Data Types & Descriptive Statistics

Variables • Quantitative Variable • A variable that is counted or measured on a numerical scale • Can be continuous or discrete (always a whole number). • Qualitative Variable • A non-numerical variable that can be classified into categories, but can’t be measured on a numerical scale. • Can be nominal or ordinal

Continuous Data • Continuous data is measured on a scale. • The data can have almost any numeric value and can be recorded at many different points. • For example • • Temperature (39. 25 o. C) Time (2. 468 seconds) Height (1. 25 m) Weight (66. 34 kg)

Discrete Data • Discrete data is also commonly referred to as Attribute data. • Discrete data is based on counts, for example; • The number of cars parked in a car park • The number of patients seen by a dentist each day. • Only a finite number of values are possible e. g. a dentist could see 10, 11, 12 people but not 12. 3 people

Nominal Data • A Nominal scale is the most basic level of measurement. The variable is divided into categories and objects are ‘measured’ by assigning them to a category. • For example, • Colours of objects (red, yellow, blue, green) • Types of transport (plane, car, boat) • There is no order of magnitude to the categories i. e. blue is no more or less of a colour than red.

Ordinal Data • Ordinal data is categorical data, where the categories can be placed in a logical order of ascendance e. g. ; • 1 – 5 scoring scale, where 1 = poor and 5 = excellent • Strength of a curry (mild, medium, hot) • There is some measure of magnitude, a score of ‘ 5 – excellent’ is better than a score of ‘ 4 – good’. • But this says nothing about the degree of difference between the categories i. e. we cannot assume a customer who thinks a service is excellent is twice as happy as one who thinks the same service is good.

Task • Look at the following variables and decide if they are qualitative or quantitative, ordinal, nominal, discrete or continuous • • Age Year of birth Sex Height Number of staff in a department Time taken to get to work Preferred strength of coffee Company size

Measures of location • Measures of location summarise the data with a single number • There are three common measures of location – Mean – Mode – Median • Quartiles are another measure

Mean • The mean (more precisely, the arithmetic mean) is commonly called the average • In formulas the mean is usually represented by read as ‘x-bar’. • The formula for calculating the mean from ‘n’ individual data-points is; X bar equals the sum of the data divided by the number of data-points

Pro’s & Con’s • Advantages • Disadvantages – It may not be an actual – basic calculation is easily understood – all data values are used in the calculation ‘meaningful’ value, e. g. an average of 2. 4 children per family. – Can be greatly affected by extreme values in a dataset. e. g. seven students take a test and receive the following scores. 40 42 45 50 53 54 99 – The average score is 54. 7 – but – used in many statistical procedures. is this really representative of the group? – If the extreme value of 99 is dropped, the average falls to 47. 3

Mode • The mode represents the most commonly occurring value within a dataset. • We usually find the mode by creating a frequency distribution in which we tally how often each value occurs. – if we find that every value occurs only once, the distribution has no mode – if we find that two or more values are tied as the most common, the distribution has more than one mode

Pro’s & Con’s • Advantages – easy to understand – not affected by outliers • Disadvantages – not all sets of data have a modal value (extreme values) – can also be obtained for qualitative data e. g. when looking at the frequency of colours of cars we may find that silver occurs most often – some sets of data have more than one modal value – multiple modal values are often difficult to interpret

Task • The following values are the ages of students in their first year of a course 18, 19, 18, 25, 22, 20, 21, 45, 33, 20, 18 • Find the mean age of the students • Find the modal value • In your opinion which is the better measure of location for this data set?

Median • Median means middle, and the median is the middle of a set of data that has been put into rank order. • Specifically, it is the value that divides a set of data into two halves, with one half of the observations being larger than the median value, and one half smaller. Half the data < 29 18 24 Half the data > 29 29 30 32

Finding the median. . . • If ‘n’ is an even number, the middle rank will fall between two observations. In this case the median is equal to the arithmetic mean of the values of the two observations 40 42 45 50 53 54 70 Position of Median = ½*(n+1) = 4. 5 Median = 99

Pro’s & Con’s • Advantages • Disadvantages – the concept is easy to – data must be arranged in rank understand – the median can be determined for any type of data (with the exception of nominal) – the median is not unduly influenced by extreme values in the dataset order (ascending or descending) – cannot combine medians in statistical calculations as with mean values

Quartiles • Also known as percentiles • Lower quartile - 25% of the data is below this • Upper quartile – 75% of the data is below this

Finding the upper quartile. . . • If a quartile lies between observations, the value of the quartile is the value of the lower observation plus the specified fraction of the difference between the two observations. 40 42 45 50 53 54 70 99 Position of Upper Quartile = ¾*(n+1) = 6. 75 Upper quartile = data-point 6 + 0. 75*(data-point 7 – data-point 6) Upper quartile = 54 + 0. 75*(70 – 54) = 66

Task • Using the student age data below, find the median and the quartiles 18, 19, 18, 25, 22, 20, 21, 45, 33, 20, 18

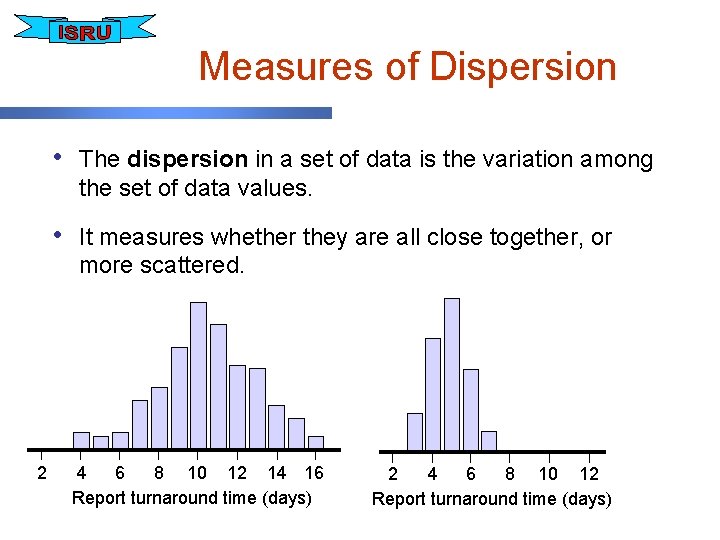
Measures of Dispersion • The dispersion in a set of data is the variation among the set of data values. • It measures whether they are all close together, or more scattered. 2 4 6 8 10 12 14 16 Report turnaround time (days) 2 4 6 8 10 12 Report turnaround time (days)

Common Measures • The four common measures of spread are • the range • the inter-quartile range • the variance • the standard deviation

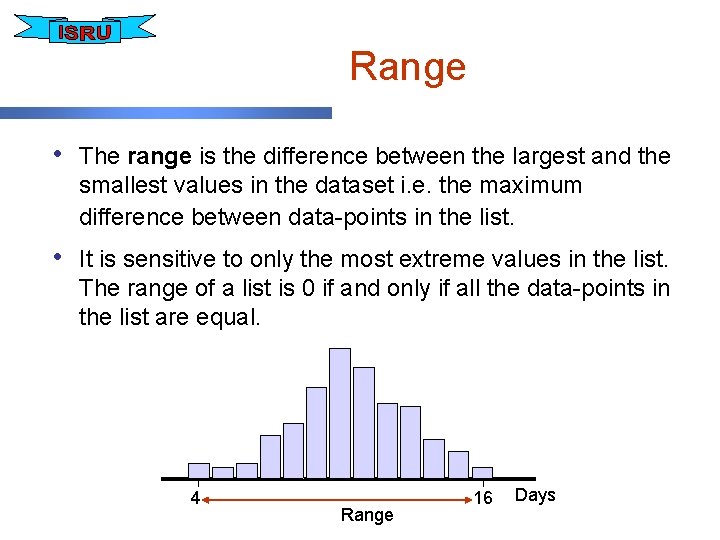
Range • The range is the difference between the largest and the smallest values in the dataset i. e. the maximum difference between data-points in the list. • It is sensitive to only the most extreme values in the list. The range of a list is 0 if and only if all the data-points in the list are equal. 4 Range 16 Days

Pro’s & Con’s • Advantages • Disadvantages – best for symmetric data – doesn’t use all of the – easy to compute and – very much affected if the – good option for ordinal – only shows maximum with no outliers understand data, only the extremes are outliers spread, does not show shape

Task • Work out a whole number data set that has the following summary statistics… ─n ─ Mean ─ Mode ─ Median ─ Range =5 =5 =5 • Are there any other possible data sets?

Inter-quartile Range • upper quartile – lower quartile • Essentially describes how much the middle 50% of your dataset varies Inter-quartile Range 4 9 Q 1 12 Q 3 20 Days

Pro’s & Con’s • Advantages • Disadvantages – Good for ordinal data – Harder to calculate and – Ignores extreme values – Doesn’t use all the information – More stable than the range because it ignores outliers understand (ignores half of the datapoints, not just the outliers) • Tails almost always matter in data and these aren’t included • Outliers can also sometimes matter and again these aren’t included.

Variance and Standard Deviation (s 2, s 2) =(population notation, sample notation) • The variance (s 2, s 2) and standard deviation (s, s) are measures of the deviation or dispersion of observations (x) around the mean ( ) • The variance is an ‘average’ deviation from the mean, squared.

Variance and Standard Deviation • The standard deviation (SD) is the square root of the variance – small SD = values cluster closely around the mean – large SD = values are scattered Mean 1 SD 4 6 8 10 1 SD 12 14 16 Days 8 Mean 10 1 SD 12

Variance and Standard Deviation • The following formulae define these measures Population Sample

Variance • Advantages • Disadvantages – uses all of the data values – the variance is measured in the original units squared – extreme values or outliers can effect the variance considerably – hard to calculate manually

Standard Deviation • Advantages • Disadvantages – uses all of the data – hard to calculate – – values same units of measurement as the values useful in theoretical work and statistical methods and inference manually

Measures of Distribution • The measures of distribution are – skewness – kurtosis • The terms skewness and kurtosis refer to distribution shapes that deviate from the shape of a normal distribution

Skewness • A skewed distribution is characterised by a tail off towards the high end of the scale (a positive skew) or towards the low end of the scale (a negative skew) Normal Distribution Positive Skew Negative Skew

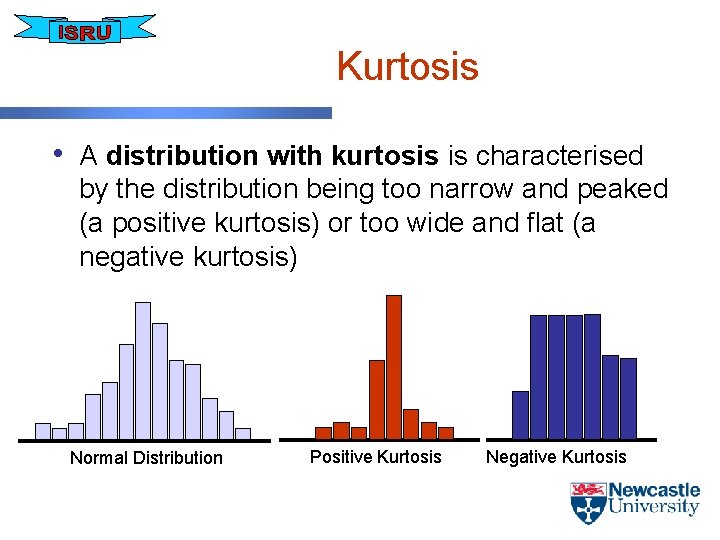
Kurtosis • A distribution with kurtosis is characterised by the distribution being too narrow and peaked (a positive kurtosis) or too wide and flat (a negative kurtosis) Normal Distribution Positive Kurtosis Negative Kurtosis

Confidence Intervals

Confidence Intervals (CI’s) • Rarely will a value calculated from sample data be exactly the same as the true value of the population • The Confidence interval (CI) is an interval within which we are confident that the true value of a population characteristic lies • CI’s are constructed using knowledge of the relevant probability distribution • A CI can be one-sided or two-sided • The mean is a common characteristic for which CI’s are constructed

Basic examples • Example of a one sided CI: 20 • Example of a two sided CI 10 20

Two sided CI’s (known variance and/or sample size 30)

95% CI for the population mean • A 95% CI for the population mean, , is given by: • Need to know sample mean, size of sample and population standard deviation

Terminology • Using 95% CI as an example: – “It is expected that 95% of the time that we take random samples and analyse the data the interval will contain the true value for the mean”

Example • Population variance is 49, sample size is 64, sample mean is 32 – Find a 95% Confidence Interval for the population mean

Answer • CI is given by:

Interpretation • Larger 2 gives wider CI, i. e. less precision • Larger n gives smaller CI, i. e. more precision

Confidence Coefficients • For a 95% confidence interval, the confidence coefficient is 1. 96 – The 95% can also be written as 100(1 - )% (where = 0. 05) • A 90% confidence interval has confidence • coefficient 1. 645 A 99% confidence interval has confidence coefficient 2. 576

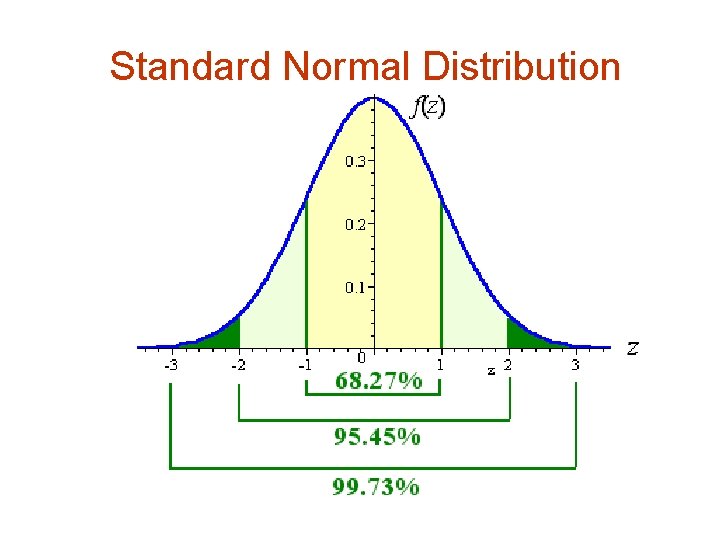
Standard Normal Distribution

CI’s for the population mean • A two sided 100(1 - )% CI for is given by: • Need to know sample mean, size of sample and • population standard deviation U refers to standardised normal values (may be referred to as Z)

Interpretation • Higher confidence, e. g. 99% leads to wider CI • Lower confidence, e. g. 90% leads to smaller CI

Other Confidence Intervals • Unknown variance and sample size < 30 • Standard deviation CI’s • One sided CI’s

Hypothesis Testing

Hypothesis Testing • Used to test whether the parameters of a distribution • – – have particular values or relationships May want to: test a hypothesis that the mean of a distribution has a certain value (one sample tests) test there is no difference between two means (two sample tests)

Example (1) • A manufacturer has 500 hours available to • • manufacture 50 products. If the time to manufacture each product is 10 hours then the manufacturing can be done on time A hypothesis test could establish that the mean time for each product to be manufactured is equal to 10

Example (2) • Two production lines are manufacturing an identical • • product It is believed that production line 1 is performing better than the other A hypothesis test could be performed on the two process means to establish whether or not production line 1 is significantly better than production line 2

Components of a Hypothesis Test • H 0 = Null hypothesis, describes the hypothesis • • being tested H 1 = Alternative hypothesis, describes the alternative hypothesis Test statistic - used to determine whether or not to reject/accept the null hypothesis

Components of a Hypothesis Test • - probability value that defines the maximum • • probability that H 0 will be rejected when it is true 1 - - the power of the test, probability that H 0 be rejected when it is false A sample of observations to be tested

H 0 and H 1 - Example (1) • H 0 = mean time for each product to be manufactured is equal to 10 – i. e. H 0: = 10 • H 1 = mean time for each product to be manufactured is not 10 – i. e. H 1: 10

H 0 and H 1 - Example (2) • H 0 = mean of each production line is the same – i. e. H 0: 1= 2 • H 1 = mean for production line 1 is better than production line 2 – i. e. H 1: 1 > 2

Possible Tests • One sided – H 0: = 0 H 1: 0 – H 0: = 0 H 1: < 0 • Two sided – H 0: = 0 H 1: 0 – H 0: 1= 2 H 1: 1 2

One Sample Tests

Some notation - reminder • Variables, such as weights, volumes, densities, • • are often referred to as x If the variable has a Normal distribution, it is often written as x~N(mean, variance) We distinguish between sample means and variances which have English letters, eg s 2 and theoretical/underlying/ population means and variances, which have Greek letters, eg 2

One Sample Tests • Address hypotheses about the true population mean or variance – if true variance is known and/ or sample size is 30 or more, use – Z (or U) values if true variance is not known and sample size <30, use t values • A test about the value of when Z (or U) is used is • called a one sample Z test A test about the value of when t is used is called a one sample t test

Use of Confidence Intervals • Can use confidence intervals for testing a hypothesis – e. g. if a sample of 100 bottles has a sample mean of 142. 23 ml and the population variance is known to be 16, is it feasible that the true mean is 143. 5 ml?

Use of Confidence Intervals Answer: • Null hypothesis, H 0: =143. 5 • Alternative hypothesis, H 1: 143. 5 • 95% CI for is[141. 449, 143. 017] – CI doesn’t include 143. 5, so reject H 0

Minitab Output One-Sample Z: data Test of mu = 143. 5 vs mu not = 143. 5 The assumed sigma = 4 Variable data N 100 Mean 142. 233 95. 0% CI ( 141. 449, 143. 017) St. Dev 4. 033 SE Mean 0. 400 Z -3. 17 P 0. 002

Summary of Hypothesis Tests • State H 0 and significance level of test • Calculate value of test statistic • Compare value with tabulated critical values or • find probability of test statistic value Conclude by rejecting/not rejecting null hypothesis

Two sample tests (comparing samples)

Comparing samples • Compare means and variances from two samples – e. g. before and after change – e. g. control and experiment – e. g. two machines, two people, two suppliers etc

Comparison of 2 samples (unknown, equal variances, and samples < 30 )

Comparison of 2 samples (unknown, equal variances, and samples < 30 ) • Compare the means of each sample ( • and ) by looking at their differences Need to estimate 2 (the true variance) by using a pooled sample variance s 2 (formed using the variance from each sample).

Two sample t test • Test the (null) hypothesis, H 0, that the 2 populations • are equal, 1 - 2 = 0 Find the t test statistic • Compare with t tables where v = n 1+ n 2 -2, 5% significance level is commonly used

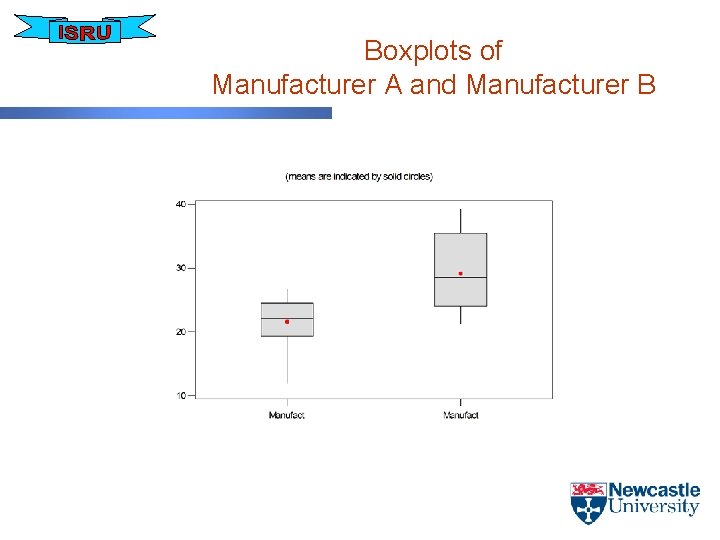
Example • Crack growth measurements for 10 samples from Manufacturer A gave – mean = 21. 57 with sample sd = 4. 32 • Measurements on 14 samples from Manufacturer B gave – mean = 29. 11 with sample sd = 6. 07 • Use the t test to compare the manufacturers

Boxplots of Manufacturer A and Manufacturer B

Minitab output Two-Sample T-Test and CI: Manufacturer A, Manufacturer B Two-sample T for Manufacturer A vs Manufacturer B Manufact N 10 14 Mean 21. 57 29. 11 St. Dev 4. 32 6. 07 SE Mean 1. 4 1. 6 Difference = mu Manufacturer A - mu Manufacturer B Estimate for difference: -7. 54 95% CI for difference: (-12. 19, -2. 88) T-Test of difference = 0 (vs not =): T-Value = -3. 35 P-Value = 0. 003 DF = 22 Both use Pooled St. Dev = 5. 42

Interpretation • If the absolute value for t is greater than the • • • corresponding critical value then the test is said to be significant. The critical value for this example is 2. 074 Absolute (-3. 35) > 2. 074, hence there is significant evidence to suggest that the means are not equal The null hypothesis is rejected - the manufacturers are different Can also look at the p-value, 0. 003 < 0. 05

Comparison of variances

Comparing variances • As well as comparing mean values, it is often • • important to compare variability between samples An appropriate test statistic is the F ratio which is calculated by dividing the two variances Critical values of the F statistic are found in tables and depend on the degrees of freedom (n 1 -1 and n 2 -1) of sample 1 and sample 2

Example • Crack growth measurements for 10 samples from one manufacturer gave – mean = 21. 57 with sample sd = 4. 32 • Measurements on 14 samples from another manufacturer gave – mean = 29. 11 with sample sd = 6. 07 • Can we assume equal variances?

Hypothesis • • – – • • Testing for equal variance between groups The hypothesis test can be expressed as follows H 0 : 1 2 = 2 2 H 1: H 0 not true Bartlett’s test (F-test) can be used when the normality assumption is valid Levene’s test can be used when normality is questionable

Test for equal variances • P-values are not significant hence do not reject the null hypothesis • The variances can be assumed to be equal

Assumptions of t and F tests • Data is approximately Normal • Data is Independent

Further Hypothesis Testing

One way ANOVA • One-way analysis of variance tests the equality of population • • • means when classification is by one factor The factor usually has three or more levels (one-way ANOVA with two levels is equivalent to a t-test), where the level represents the treatment applied For example, if you conduct an experiment where you measure durability of a product made by one of three methods, these methods constitute the levels The one-way procedure also allows you to examine differences among means using multiple comparisons

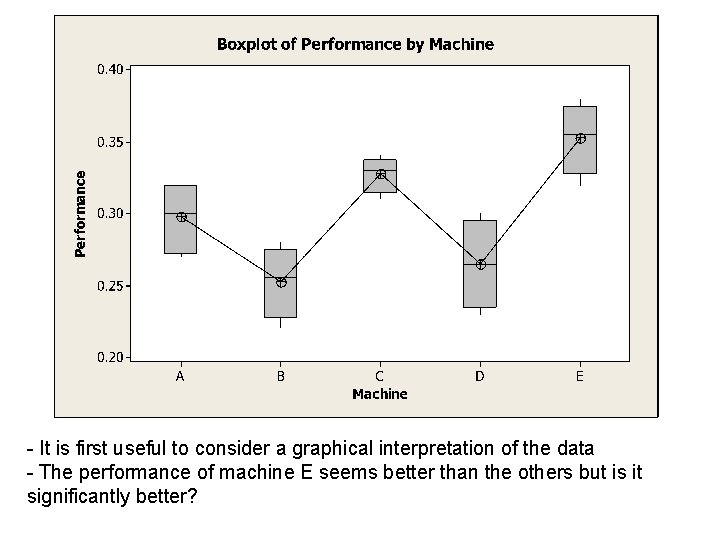
Example – One Way ANOVA • Five machines are run in the factory and a measure of performance is evaluated at the end of each day. The measurements are given above • What do they tell us about the machines?

- It is first useful to consider a graphical interpretation of the data - The performance of machine E seems better than the others but is it significantly better?

ANOVA for one factor at 5 levels One-way ANOVA: Measure versus Machine Analysis of Variance for Measure Source DF SS MS Machine 4 0. 027980 0. 006995 Error 15 0. 009200 0. 000613 Total 19 0. 037180 F 11. 40 P 0. 000 • If you put the performance data into a software package the above output is obtained

Hypothesis test • The basis of the One-way ANOVA is to determine if the factor’s level means are all the same or there are differences • The hypothesis test can be expressed as follows: – H 0: 1= 2=… a where a = number of factor levels – HA: i j for at least one pair (i, j)

p-value • The Null Hypothesis is tested by calculating the F statistic • The p-value is a probability corresponding to the F statistic - if it is small (< 0. 05) there is evidence of real differences among the machines (reject the null hypothesis) - if it is large ( > 0. 05) then we have no evidence of real differences (do not reject the null hypothesis)

Machines example One-way ANOVA: Measure versus Machine Analysis of Variance for Measure Source DF SS MS Machine 4 0. 027980 0. 006995 Error 15 0. 009200 0. 000613 Total 19 0. 037180 F 11. 40 P 0. 000 – p value < 0. 05 – differences between the performances of the machines

Where are the differences? Level A B C D E N 4 4 4 Mean 0. 29750 0. 25250 0. 32750 0. 26500 0. 35250 St. Dev 0. 02630 0. 02500 0. 01258 0. 03109 0. 02500 Individual 95% CIs For Mean Based on Pooled St. Dev ---+---------+-----+-----(-----*------) (------*-----) (-----*------) ---+---------+-----+-----0. 240 0. 280 0. 320 0. 360 Pooled St. Dev = 0. 02477 Machine E differs significantly from machines A, B and D because its confidence interval doesn’t overlap with theirs Machine C differs from machines B and D for the same reason

Task • Think of 5 scenarios either in the workplace or everyday life where ANOVA could be utilised • Determine for each scenario: – Factors – Factor levels – Response • Discuss in pairs and then share your answers with the group

Two way ANOVA • Two-way analysis of variance performs an analysis of variance for testing the equality of population means when classification of treatments is by two factors • In two-way ANOVA, the data must be balanced (all cells must have the same number of observations) and factors must be fixed

Non-parametric methods • Non-parametric tests are used when there are no assumptions about a specific distribution for the population • They are more robust against violation of the assumptions made • These tests are equivalent to parametric tests ─ One sample sign / One sample z or t ─ One sample Wilcoxon / One sample z or t ─ Mann-Whitney / Two sample z or t ─ Kruskall-Wallis / One way ANOVA ─ Mood’s median / One way ANOVA ─ Friedman’s test / Two way ANOVA

ANOVA and Regression • Analysis of variance (ANOVA) is similar to regression in • that it is used to investigate and model the relationship between a response variable and one or more independent variables However, analysis of variance differs from regression in that the independent variables are qualitative (categorical) in ANOVA

Regression and Correlation

Regression • Regression is a branch of statistics which • • models situations Regression is used to examine the relationship between an output variable and one or more input variables. Regression allows us to; • Determine whether an input significantly affects the output • Predict the behaviour of the output based on the input.

Relationships Between Variables • Suppose we were collecting data on blood • • pressure. Observation of a number of individuals could tell us that blood pressure is related to the age of the individual. Can we investigate whethere is a relationship between systolic blood pressure and age? Yes - using regression.

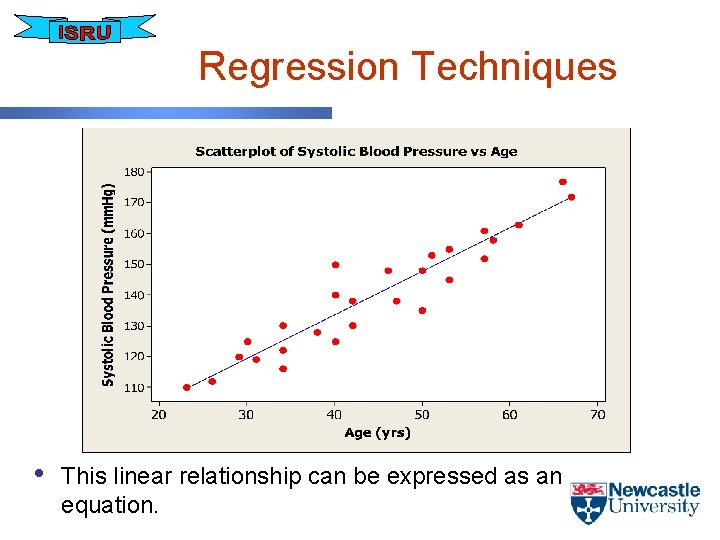
Example - Regression • Example – A sample of 27 office workers were randomly selected. The systolic blood pressure of each individual was measured over a set period of time and an average found • Initial step - look at a scatter plot of Blood Pressure vs Age

Reminder - Scatter Plot • Visual representation of the relationship between • • • two variables Random scatter (no apparent pattern) - variables have no correlation and are not related Visible pattern - indication of a relationship between variables Be careful - apparent relationships may be purely circumstantial !

Scatter plot of Blood Pressure vs Age

Correlation • It appears from the scatter plot that blood pressure • • increases with age. The relationship isn’t perfect – but generally the two variables increase and decrease together. We can measure the strength and direction of this relationship using a correlation statistic. Correlation implies that as one variable changes, the other changes. The Pearson Correlation Coefficient (r) is a statistic that can be used to express quantitatively the magnitude and direction of the linear relationship between two variables.

Correlation • r takes values between -1 and 1 • -1 indicates perfect negative correlation • 1 indicates perfect positive correlation • 0 indicates no correlation • Note – correlation does not imply that one variable is the ‘cause’ of another i. e. it does not imply that y increases because x increases.

Minitab Output Pearson correlation of Systolic Blood Pressure and Age = 0. 942 P-Value = 0. 000 • A correlation coefficient of 0. 942 indicates that • there is a strong positive correlation between the two variables. The p-value of 0. 000 indicates that the test is highly significant.

Regression Techniques • This linear relationship can be expressed as an equation.

Simple Linear Regression Equation • • • y is the dependent variable x is the independent variable 0 is used to estimate the intercept on the Y axis 1 is used to indicate the slope of the regression line ε is a random, independent error term

Regression Techniques • Unlike correlation, Regression does treat one variable (y) as the outcome to the other variable (x). • x is the explanatory variable, also commonly called the independent variable, covariate, regressor or predictor. • y is the response variable, also called the dependent • variable The error term is included in the model equation to acknowledge the fact that there will be some unpredictability in the outcome

Fitting the Regression Line • If the scatter plot of y vs x looks approximately • • linear, how do we decide where to put the regression line? By eye? A standard procedure for fitting the line of best fit is necessary, otherwise the model fitted to the data would change depending on who was examining the data.

Fitting the Regression Line • The least squares method is used to achieve this. • Least squares minimises the sum of squared vertical differences between the observed y values and the line. • I. e. the least squares regression line minimises the • error between the predicted values of y and the actual y values. The total prediction error is less for the least-squares regression line than for any other possible prediction line.

Fitting the Regression Line

Least Squares Estimators for Parameters • • The regression line (the line of best fit) passes through the point ( and ) and predicts the value of y for any given x The intercept is estimated by: • The slope of the line is estimated by:

Minitab Output • Using Stat-Regression in Minitab, setting the variable “Blood Pressure” as the response variable and “Age” as the predictor gives the following result. The regression equation is Blood Pressure = 76. 8 + 1. 41 Age • • Estimate of Intercept ( ) = 76. 8 Estimate of Slope ( ) = 1. 41

Regression Equation • Predicting the blood pressure for a new individual who is 35 years of age Systolic Blood Pressure = 76. 8 + 1. 41 Age Systolic Blood Pressure = 76. 8 + 1. 41 x 35 = 126. 15 mm. Hg

Fitted Values and Residuals • The predicted y values are also called the fitted y values and can be written as; • The differences between the observed y values and the fitted y values are called the residuals • The residuals are given by:

Significance Tests on the Regression Coefficients Involve the t test • Test on 0 • H 0: 0 = zero • H 1: 0 zero • Test on 1 • H 0: 1 = zero • H 1: 1 zero

Minitab Output for Regression Model The regression equation is Blood Pressure = 76. 8 + 1. 41 Age Predictor Constant Age Coef 76. 843 1. 4139 SE Coef 4. 629 0. 1006 • The test on the intercept T 16. 60 14. 05 P 0. 000 has a p-value of 0. 000 (Significant). • The test on has a p-value of 0. 000 (significant). • In both cases the null hypothesis can be rejected – there is evidence that a non-zero intercept and a non -zero slope are feasible.

Residuals • Residuals have an important role in • determining the adequacy of the fitted model and detecting deviations from the model Residual analysis can check for: • Normality • Correlation between residuals • Correctness of the model through the full range of fitted values • Outliers

What to do with unusual points? • These often arise in practice • There is often no satisfactory explanation for • • them May be risky to leave them out of the analysis but it may be worthwhile re-analysing the data without the unusual points

If the model is inadequate • There may be a need to: • Add in more variables (multiple regression) • Add in a higher order term e. g. an x 2 or x 3 term (i. e. not a simple linear model) • Transform the data

Task • Think of 5 scenarios either in the workplace or everyday life where Regression techniques could be utilised • Determine for each scenario: – Factors – Response • Discuss in pairs and then share your answers with the group

Summary • Data Types & Descriptive Statistics • Confidence Intervals • Hypothesis Testing • Two Sample Tests • Further Hypothesis Testing (inc. ANOVA & Regression)