Statistics We collect a sample of data what

Statistics ØWe collect a sample of data, what do we do with it? n n Estimate parameters (possibly of some model) Test whether a particular theory is consistent with our data (hypothesis testing) ØStatistics is a set of tools that allows us to achieve these goals 1

Statistics Ø Preliminaries 2

Statistics Ø Some common estimators are for the mean and variance 3

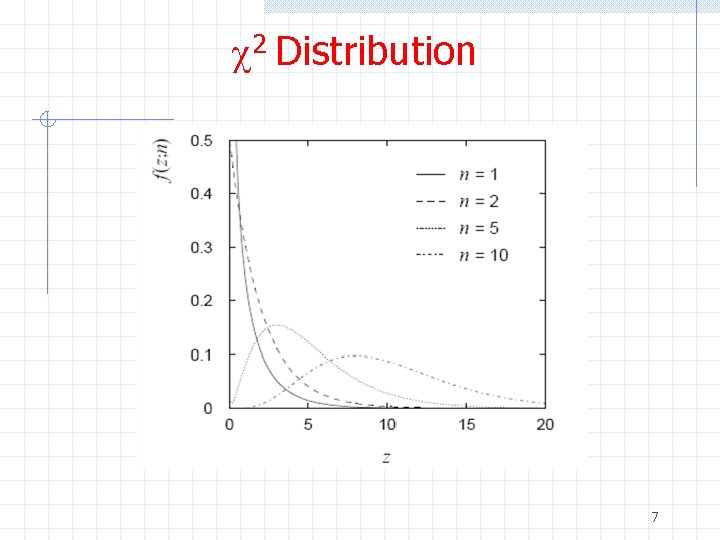
c 2 Distribution Ø A common situation is that you have a set of measurements xi and you know the true value of each xit n How good are our measurements? Ø Similarly you may be comparing a histogram of data with another that contains expectation values under some hypothesis n How well do the data agree with this hypothesis? Ø Or if parameters of a function were estimated using the method of least squares, a minimum value of c 2 was obtained n How good was the fit? 4

c 2 Distribution Ø Assuming n n The measurements are independent of each other The measurements come from a Gaussian distribution Ø One can use the “goodness-of-fit” statistic c 2 to answer these questions w In the case of Poisson distributed numbers, si 2=xti, this is called Pearson’s c 2 statistic 5

c 2 Distribution Ø Chi-square distribution 6

c 2 Distribution 7

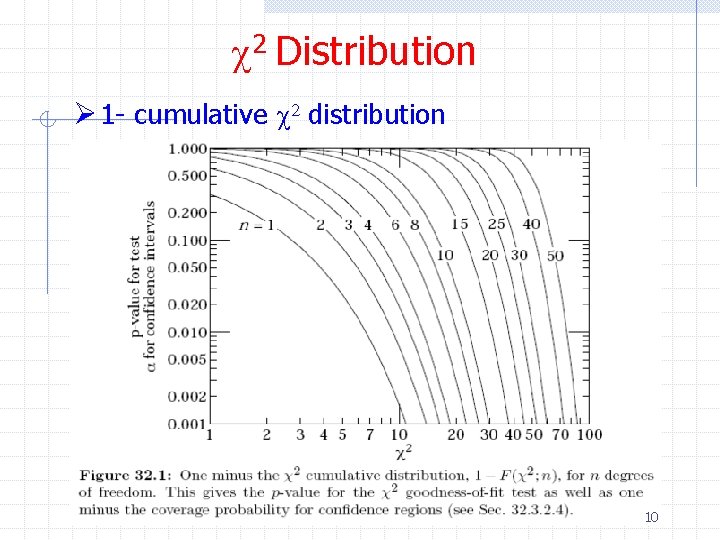
c 2 Distribution ØThe integrals (or cumulative distributions) between arbitrary points for both the Gaussian and c 2 distributions cannot be evaluated analytically and must be looked up n n What is the probability of getting a c 2 > 10 with 4 degrees of freedom? This number tells you the probability that random fluctuations (chance fluctuations) in the data would give a value of c 2 > 10 8

c 2 Distribution Ø Note the p-value is defined as Ø We’ll come back to p-values in a moment 9

c 2 Distribution Ø 1 - cumulative c 2 distribution 10

c 2 Distribution ØOften one uses the reduced c 2 = c 2/n 11

Hypothesis Testing Ø Hypothesis tests provide a rule for accepting or rejecting hypotheses depending on the outcome of a measurement 12

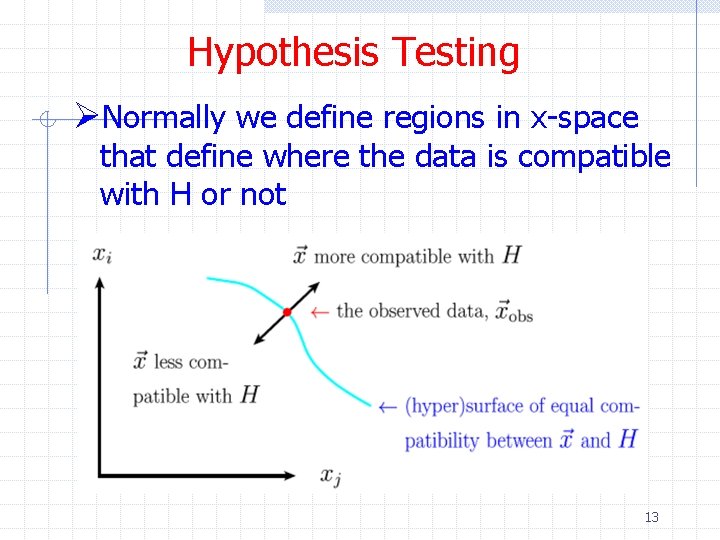
Hypothesis Testing ØNormally we define regions in x-space that define where the data is compatible with H or not 13

Hypothesis Testing Ø Let’s say there is just one hypothesis H Ø We can define some test statistic t whose value in some way reflects the level of agreement between the data and they hypothesis Ø We can quantify the goodness-of-fit by specifying a p-value given an observed tobs in the experiment n n Assumes t is defined such that large values correspond to poor agreement with the hypothesis g is the pdf for t 14

Hypothesis Testing ØNotes n n n p is not the significance level of the test p is not the confidence level of a confidence interval p is not the probability that H is true w That’s Bayesian speak n p is the probability, under the assumption of H, of obtaining data (x or t(x)) having equal or lesser compatibility with H as xobs 15

Hypothesis Testing Ø Flip coins n n Hypothesis H is coin is fair (random) so ph=pt=0. 5 We could take t=|nh-N/2| Ø Toss coin N=20 times and observe nh=17 Ø Is H false? n n n Don’t know We can say that probability of observing 17 or more heads assuming H is 0. 0026 16 p is the probability of observing this result “by chance”

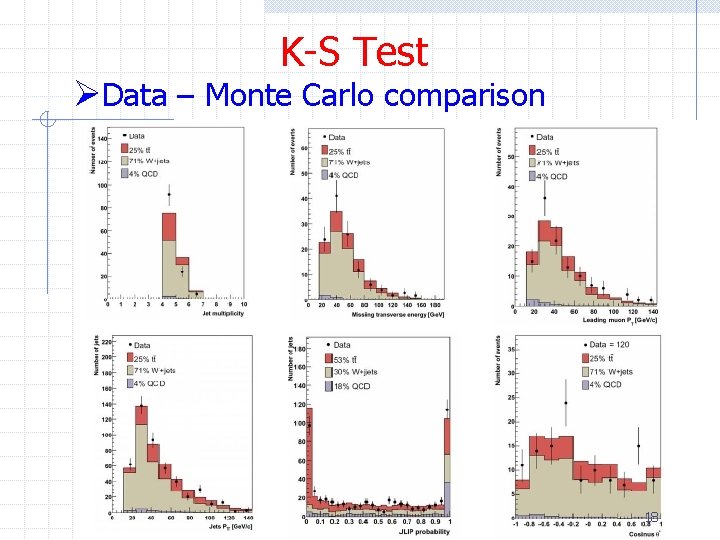
Kolmogorov-Smirnov (K-S) Test ØThe K-S test is an alternative to the c 2 test when the data sample is small ØIt is also more powerful than the c 2 test since it does not rely on bins – though one commonly uses it that way n A common use is to quantify how well data and Monte Carlo distributions agree ØIt also does not depend on the underlying cumulative distribution function being tested 17

K-S Test ØData – Monte Carlo comparison 18

K-S Test Ø The K-S test is based on the empirical distribution function (ECDF) Fn(x) n For n ordered data points yi Ø This is a step function that increases by 1/N at the value of each ordered data point 19

K-S Test Ø The K-S statistic is given by Ø If D > some critical value obtained from tables, the hypothesis (data and theory distributions agree) is rejected 20

K-S Test 21

Statistics ØSuppose N independent measurements xi are drawn from a pdf f(x; q) ØWe want to estimate the parameters q n n The most important method for doing this is the method of maximum likelihood A related method in the case of least squares 22

Hypothesis Testing Ø Example n n Properties of some selected events Hypothesis H is these are top quark events Ø Working in x-space is hard so usually one constructs a test statistic t instead whose value reflects the compatibility between the data vector x and H n n Low t – data more compatible with H High t – data less compatible with H Ø Since f(x, H) is known, g(t, H) can be determined 23

Hypothesis Testing Ø Notes n n n p is not the significance level of the test p is not the confidence level of a confidence interval p is not the probability that H is true w That’s Bayesian speak n p is the probability, under the assumption of H, of obtaining data (x or t(x)) having equal or lesser compatibility with H as xobs Ø Since p is a function of r. v. x, p itself is a r. v n n If H is true, p is uniform in [0, 1] If H is not true, p is peaked closer to 0 24

Hypothesis Testing Ø Suppose we observe nobs=ns+nb events n n ns, nb are Poisson r. v. ’s with means ns, nb nobs=ns+nb is Poisson r. v. with mean n=ns+nb 25

Hypothesis Testing Ø Suppose nb=0. 5 and we observe nobs=5 n Publish/NY Times headline or not? Ø Often we take H to be the null hypothesis – assume it’s random fluctuation of background n n Assume ns=0 This is the probability of observing 5 or more resulting from chance fluctuations of the background 26

Hypothesis Testing Ø Another problem, instead of counting events say we measure some variable x n Publish/NY Times headline or not? 27

Hypothesis Testing Ø Again take H to be the null hypothesis – assume it’s random fluctuation of background n Assume ns=0 Ø Again p is the probability of observing 11 or more events resulting from chance fluctuations of the background n n How did we know where to look / how to bin? Is the observed width consistent with the resolution in x? Would a slightly different analysis still show a peak? What about the fact that the bins on either side of the peak are low? 28

Least Squares Ø Another approach is to compare a histogram with a hypothesis that provides expectation values n n n In this case we’d compare a vector of Poisson distributed numbers (the histogram) with their expectation values ni=E[ni] This is called Pearson’s statistic If the ni are not too small (e. g. ni > 5) then the observed c 2 will follow the chi-square pdf for N dof w Or more generally for N – number of fitted parameters w Same will hold true for N independent measurements yi that are Gaussian distributed 29

Least Squares Ø We can calculate the p-value as Ø In our example 30

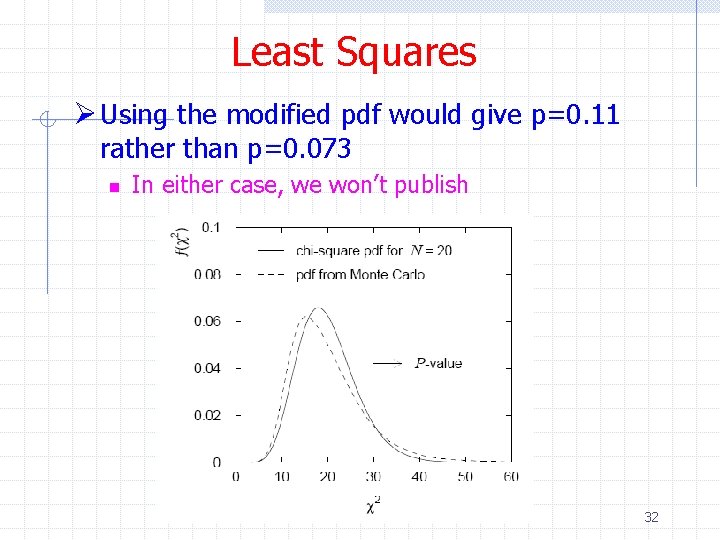
Least Squares ØIn our example though we have many bins with a small number of counts or 0 ØWe can still use Pearson’s test but we need to determine the pdf f(c 2) by Monte Carlo n n n Generate ni from Poisson, mean ni in each bin Compute c 2 and record in a histogram Repeat for a large number of times (see next slide) 31

Least Squares Ø Using the modified pdf would give p=0. 11 rather than p=0. 073 n In either case, we won’t publish 32

K-S Test Ø Usage in ROOT n n n TFile * data TFile * MC TH 1 F * jet_pt = data → Get(“h_jet_pt”) TH 1 F * MCjet_pt = MC → Get(“h_jet_pt”) Double_t KS=MCjet_pt→Kolmogorov. Test(jet_pt) Ø Notes n The returned value is the probability of the test w << 1 means the two histograms are not compatable n The returned value is not the maximum KS distance though you can return this with option “M” Ø Also available in statistical toolbox in Mat. Lab 33

Limiting Cases Binomial Poisson Gaussian 34

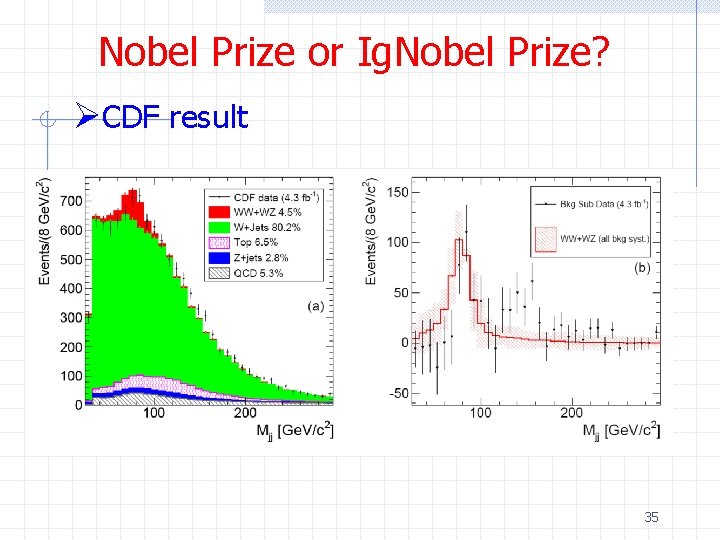
Nobel Prize or Ig. Nobel Prize? ØCDF result 35

Kaplan-Meier Curve ØA patient is treated for a disease. What is the probability of an individual surviving or remaining disease-free? n n n Usually patients will be followed for various lengths of time after treatment Some will survive or remain disease-free while others will not. Some will leave the study. A nonparametric method can be found using w Kaplan-Meier curve w Life table w Survival curve 36

Kaplan-Meier Curve ØCalculate a conditional probability n S(t. N) = P(t 1) x P(t 2) x P(t 3) x … P(t. N) w The survival function S(t) is equivalent to the empirical distribution function F(t) n We can write this as 37

Kaplan-Meier Curve 38

Kaplan-Meier Curve ØThe square root of the variance of S(t) can be calculated as ØAssuming the pk follow a Gaussian (normal) distribution, then the 95% CL will be 39

Gaussian Confidence Interval 40

Gaussian Confidence Interval 41

Gaussian Distribution Ø Some useful properties of the Gaussian distribution are in range m±s) = 0. 683 in range m± 2 s) = 0. 9555 in range m± 3 s) = 0. 9973 outside range m± 3 s) = 0. 0027 outside range m± 5 s) = 5. 7 x 10 -7 n P(x P(x P(x n P(x in range m± 0. 6745 s) = 0. 5 n n 42

Gaussian Distribution 43

Confidence Intervals ØSuppose you have a bag of black and white marbles and wish to determine the fraction f that are white. How confident are you of the initial composition? How does your confidence change after extracting n black balls? ØSuppose you are tested for a disease. The test is 100% accurate if you have the disease. The test gives 0. 2% false positive if you do not. The test comes back positive. What is the probability 44

Confidence Intervals Ø Suppose you are searching for the Higgs and have a well-known expected background of 3 events. What 90% confidence limit can you set on the Higgs cross section n if you observe 0 events? n if you observe 3 events? n if you observe 10 events? Ø The ability to set confidence limits (or claim discovery) is an important part of frontier physics ØHow to do this the “correct” way is somewhat/very controversial 45

Confidence Intervals Ø Questions n n n What is the mass of the top quark? What is the mass of the tau neutrino What is the mass of the Higgs Ø Answers n n n Mt = 172. 5 ± 2. 3 Ge. V Mv < 18. 2 Me. V MH > 114. 3 Ge. V Ø More correct answers n n n Mt = 172. 5 ± 2. 3 Ge. V with CL = 0. 683 0 < Mv < 18. 2 Me. V with CL = 0. 95 Infinity > MH > 114. 3 Ge. V with CL = 0. 95 46

Confidence Interval ØA confidence interval reflects the statistical precision of the experiment and quantifies the reliabiltiy of a measurement ØFor a sufficiently large data sample, the mean and standard deviation of the mean provide a good interval n n n What if the pdf isn’t Gaussian? What if there are physical boundaries? What if the data sample is small? ØHere we run into problems 47

Confidence Interval ØA dog has a 50% probability of being 100 m from its master n You observe the dog, what can you say about its master? w With 50% probability, the master is within 100 m of the dog w But this assumes n n The master can be anywhere around the dog The dog has no preferred direction of travel 48

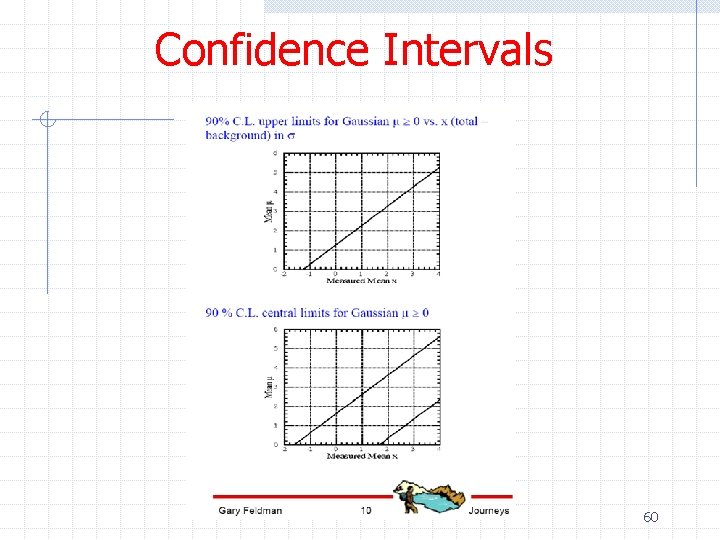
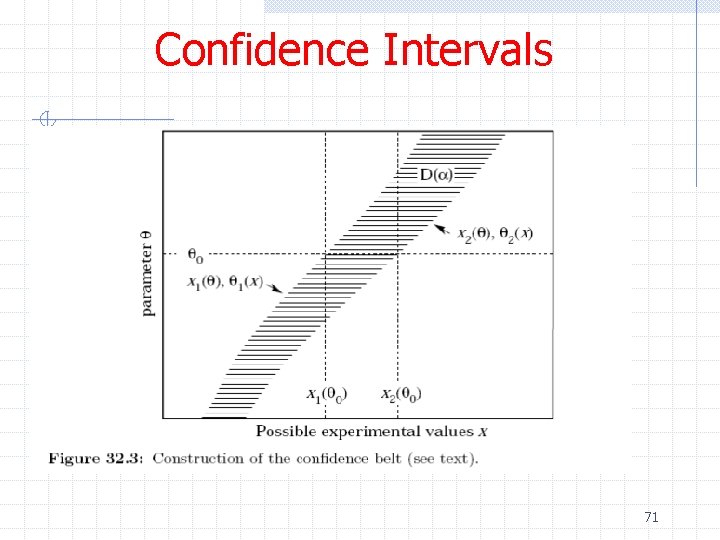
Confidence Intervals ØNeyman’s construction n Consider a pdf f(x; θ) = P(x|θ) For each value of θ, we construct a horizontal line segment [x 1, x 2] such that P(x Î[x 1, x 2]|θ) = 1 -a The union of such intervals for all values of θ is called the confidence belt 49

Confidence Intervals ØNeyman’s construction n n After performing an experiment to measure x, a vertical line is drawn through the experimentally measured value x 0 The confidence interval for θ is the set of all values of θ for which the corresponding line segment [x 1, x 2] is intercepted by the vertical line 50

Confidence Intervals 51

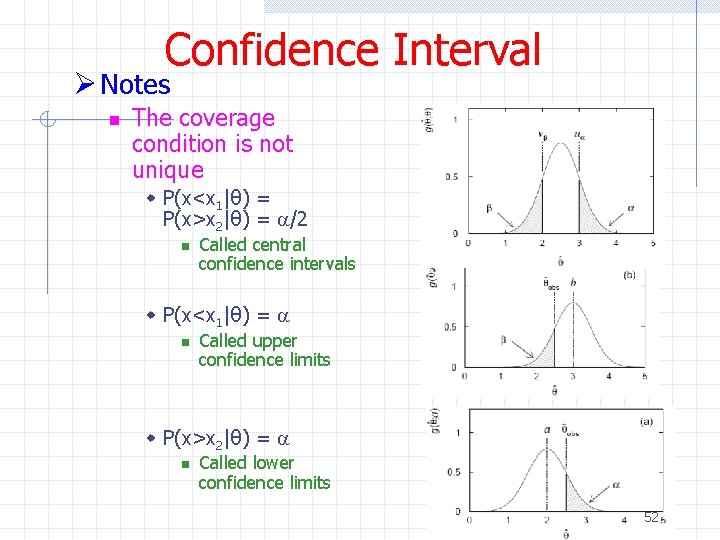
Confidence Interval Ø Notes n The coverage condition is not unique w P(x<x 1|θ) = P(x>x 2|θ) = a/2 n Called central confidence intervals w P(x<x 1|θ) = a n Called upper confidence limits w P(x>x 2|θ) = a n Called lower confidence limits 52

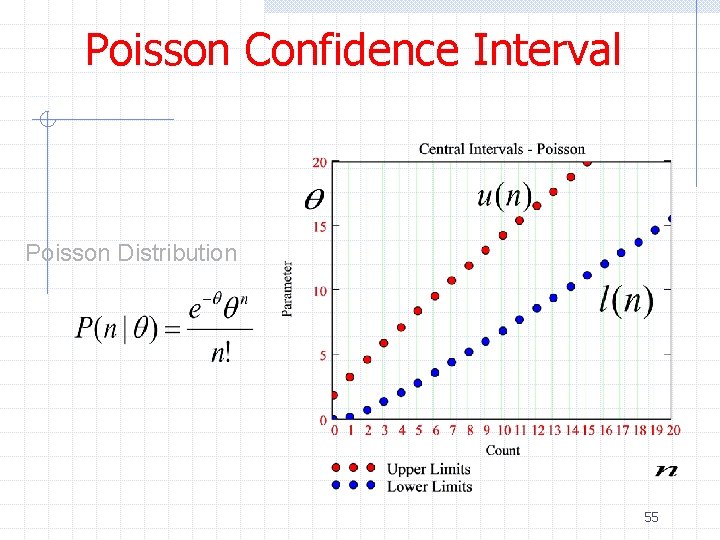
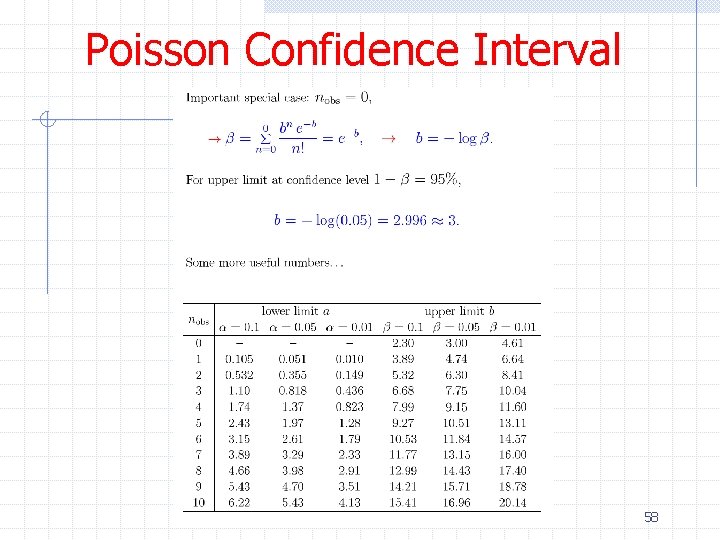
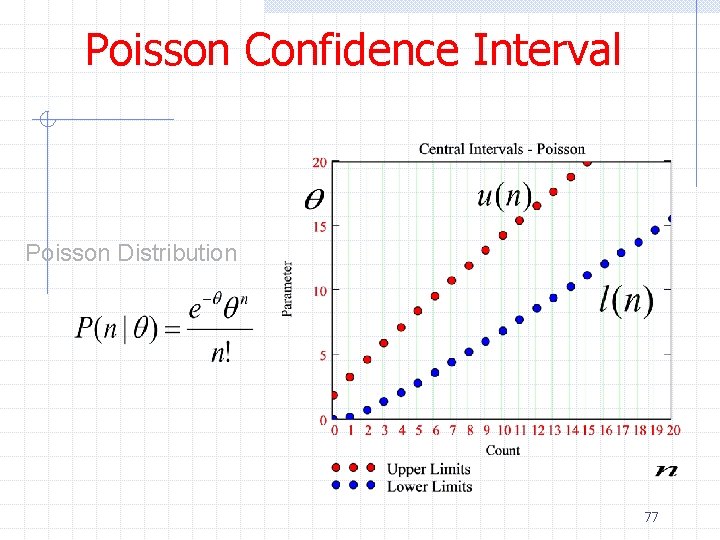
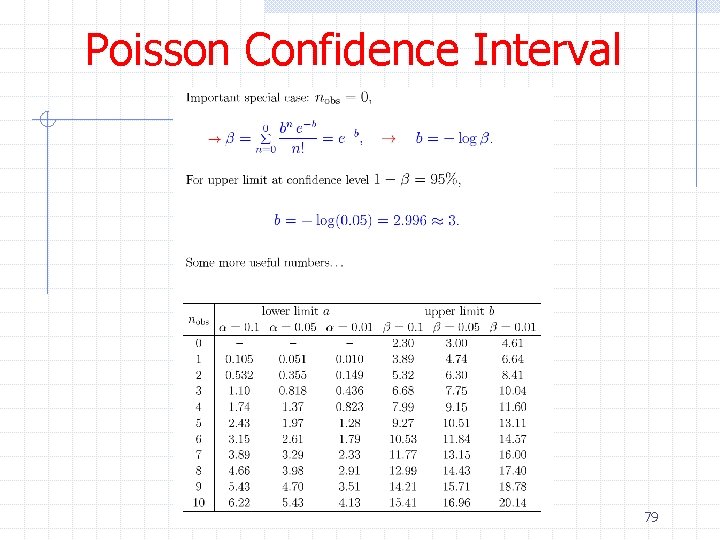
Poisson Confidence Interval ØWe previously mentioned that the number of events produced in a reaction with cross section σ and fixed luminosity L follows a Poisson distribution with mean n=σ∫Ldt n n P(n; v) = e-n nn / n! If the variables are discrete by convention one constructs the confidence belt by requiring P(x 1<x<x 2|θ) >= 1 -a ØExample: Measuring the Higgs production cross section assuming no background 53

Poisson Confidence Interval 54

Poisson Confidence Interval Poisson Distribution 55

Poisson Confidence Interval 56

Poisson Confidence Interval Ø Assume signal s and background b 57

Poisson Confidence Interval 58

Confidence Intervals ØSometimes though confidence intervals n n Are empty Reduce in size when the background estimate increases Are smaller for a poorer experiment Exclude parameters for which the experiment is insensitive ØExample n n n We know that P(x=0|v=2. 3) = 0. 1 v < 2. 3 @ 90% CL If the number of background events b is 3, 59 then since v = s + b, number of signal events

Confidence Intervals 60

Confidence Intervals 61

Confidence Interval ØExperiment X uses a fit to extract the neutrino mass n n Mv = -4 ± 2 e. V => P (Mv < 0 e. V) = 0. 98? 62

Confidence Interval ØWhat is probability? n Frequentist approach w Developed by Venn, Fisher, Neyman, von Mises w The relative frequency with which something happens w number of successes / number of trials n Venn limit (n trials to infinity) w Assumes success appeared in the past and will occur in the future with the same probability n It will rain tomorrow in Tucson and P(S) = 0. 01 w The relative frequency it rains on Mondays in 63 April is 0. 01

Confidence Interval Ø What is probability n Bayesian approach w Developed by Bayes, Laplace, Gauss, Jeffreys, de Finetti w The degree of belief or confidence of a statement or measurement w Closer to what is used in everyday life n Is the Standard Model correct w Similar to betting odds w Not “scientific”? n It will rain tomorrow in Tucson and P(S) = 0. 01 w The plausibility of the above statement is 0. 01 (ie the same as if I were to draw a white ball out of a container of 100 balls, 1 of which is white) 64

Confidence Interval ØUsually n n Confidence interval == frequentist confidence interval Credible interval == Bayesian posterior probability interval w But you’ll also hear Bayesian confidence interval ØProbability n P=1–a w a = 0. 05 => P = 95% 65

Confidence Interval Ø Suppose you wish to determine a parameter θ whose true value is θt is unknown Ø Assume we make a single measurement of an observable x whose pdf P(x|θ) depends on θ n Recall this is the probability of obtaining x given θ Ø Say we measure x 0, then we obtain P(x 0|θ) Ø Frequentist n Makes statements about P(x|θ) Ø Bayesian n n Makes statements about P(θt|x 0) = P(x 0|θt) P(θt) / P(x 0) Ø We’ll stick with the frequentist approach for the moment 66

Confidence Interval Ø (Frequentist) confidence intervals are constructed to include the true value of the parameter (θt) with a probability of 1 -α n In fact this is true for any value of θ Ø A confidence interval [θ 1, θ 2] is a member of a set, such that the set has the property that P(θÎ [θ 1, θ 2])= 1 -α n n Perform an ensemble of experiments with fixed θ The interval [θ 1, θ 2] will vary and cover the fixed value θ in a fraction of 1 -α of the experiments Ø Presumably when we make a measurement we are selecting it at random from the ensemble that contains the true value of θ, θt Ø Note we haven’t said anything about the probability of θt being in the interval [θ 1, θ 2] as 67 a Bayesian would

Confidence Interval ØIf P(θ Î[θ 1, θ 2]) = 1 -a is true we say the intervals “cover” θ at the stated confidence ØIf there are values of θ for which P(θ Î[θ 1, θ 2]) < 1 -a we say the intervals “undercover” for that θ ØIf there are values of θ for which P(θ Î[θ 1, θ 2]) > 1 -a we say the intervals “overcover” for that θ ØUndercoverage is bad 68

Confidence Intervals ØNeyman’s construction n Consider a pdf f(x; θ) = P(x|θ) For each value of θ, we construct a horizontal line segment [x 1, x 2] such that P(x Î[x 1, x 2]|θ) = 1 -a The union of such intervals for all values of θ is called the confidence belt 69

Confidence Intervals ØNeyman’s construction n n After performing an experiment to measure x, a vertical line is drawn through the experimentally measured value x 0 The confidence interval for θ is the set of all values of θ for which the corresponding line segment [x 1, x 2] is intercepted by the vertical line 70

Confidence Intervals 71

Confidence Interval Ø Notes n The coverage condition is not unique w P(x<x 1|θ) = P(x>x 2|θ) = a/2 n Called central confidence intervals w P(x<x 1|θ) = a n Called upper confidence limits w P(x>x 2|θ) = a n Called lower confidence limits 72

Confidence Intervals ØThese confidence intervals have a confidence level = 1 -a ØBy construction, P(θ Î[θ 1, θ 2]) > 1 -a is satisfied for all θ including θt ØAnother method is to consider a test of the hypothesis that the parameters true value is θ ØIf the variables are discrete by convention one constructs the confidence belt by requiring 73 P(x <x<x |θ) >= 1 -a

Examples ØData consisting of a single random variable x that follows a Gaussian distribution ØCounting experiments 74

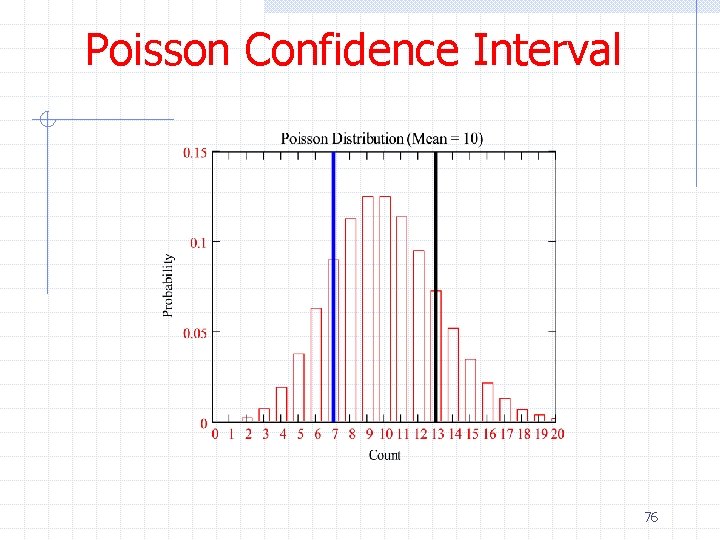
Poisson Confidence Interval ØWe previously mentioned that the number of events produced in a reaction with cross section σ and fixed luminosity L follows a Poisson distribution with mean v=σ∫Ldt n n P(n; v) = e-v vn / n! If the variables are discrete by convention one constructs the confidence belt by requiring P(x 1<x<x 2|θ) >= 1 -a ØExample: Measuring the Higgs production cross section assuming no 75

Poisson Confidence Interval 76

Poisson Confidence Interval Poisson Distribution 77

Poisson Confidence Interval 78

Poisson Confidence Interval 79

Confidence Intervals ØSometimes though confidence intervals n n Are empty Reduce in size when the background estimate increases Are smaller for a poorer experiment Exclude parameters for which the experiment is insensitive ØExample n n n We know that P(x=0|v=2. 3) = 0. 1 v < 2. 3 @ 90% CL If the number of background events b is 3, 80 then since v = s + b, number of signal events

Confidence Intervals 81

Confidence Intervals 82