Statistics Sampling Intervals for a Single Sample Contents

Statistics Sampling Intervals for a Single Sample Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Confidence Interval on the Mean of a Normal Distribution, Variance Known If , , …, are normally and independently distributed with unknown mean and known variance has a standard normal distribution

Confidence interval on the mean, variance known Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

From , we have If is used as an estimate of , we can be confident that the error will not exceed a specified amount when the sample size is Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

One-sided confidence bounds on the mean, variance known ◦A is upper-confidence bound for ◦A is lower-confidence bound for Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

General method to derive a confidence interval ◦ We find a statistic that 1. depends on both the sample and 2. The probability distribution of does not depend on and any other unknown parameter For example, ◦ Find constants and so that

Large-sample confidence interval on the mean When is large, the quantity has an approximate standard normal distribution. Consequently, is a large-sample confidence interval for with confidence level of approximately. , Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Large-sample approximate confidence interval If the quantity has an approximate standard normal distribution. Consequently, is a large-sample approximate confidence interval for Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Example 8 -1 Metallic Material Transition ◦ Ten measurements: 64. 1, 64. 7, 64. 5, 64. 6, 64. 5, 64. 3, 64. 6, 64. 8, 64. 2, 64. 3 ◦ Assume it is a normal distribution with. Find a 95% CI for. Example 8 -2 Metallic Material Transition ◦ Determine how many specimens must be tested to ensure that the 95% CI for has a length of at most 1. 0. Example 8 -3 One-Sided Confidence Bound Contents, figures, and exercises come from the textbook: Applied ◦ Determine a lower, one-sided 95% CI Statistics for. and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Example 8 -4 Mercury Contamination ◦ 53 measurements: 1. 230, 0. 490, … ◦ , , , ◦ Find a 95% CI for. . Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Exercise 8 -14 ◦ The life in hours of a 75 -watt light bulb is known to be normally distributed with hours. A random sample of 20 bulbs has a mean life of hours. ◦ (a) Construct a 95% two-sided confidence interval on the mean life. ◦ (b) Construct a 95% lower-confidence bound on the mean life. Compare the lower bound of this confidence interval with the one in part (a). Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Confidence Interval on the Mean of a Normal Distribution, Variance Unknown Distribution Let , , …, are normally and independently distributed with unknown mean and unknown variance. The random variable has a distribution with degrees of freedom.

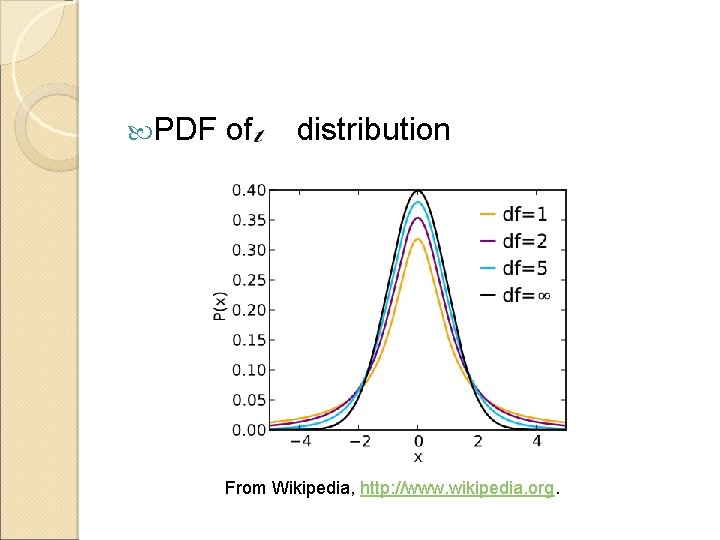
PDF of distribution From Wikipedia, http: //www. wikipedia. org.

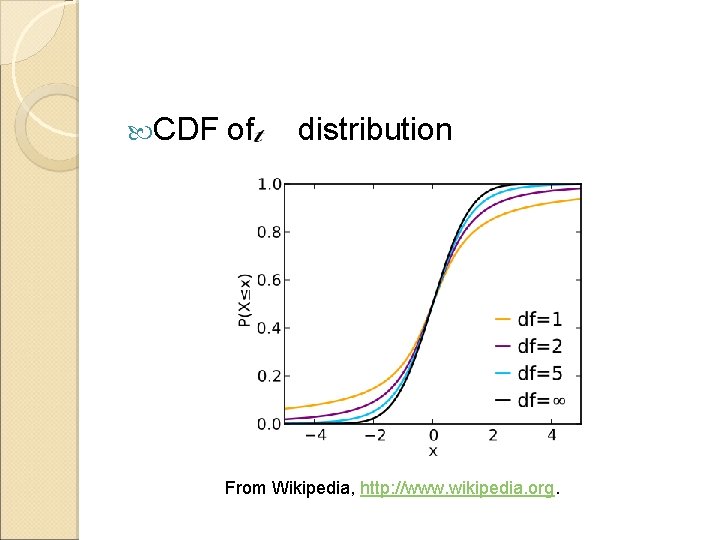
CDF of distribution From Wikipedia, http: //www. wikipedia. org.

The probability density function is the number of degrees of freedom Mean : Variance : for ◦ Percentage points Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

confidence interval on Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Confidence interval on the mean, variance unknown ◦ If and are the mean and standard deviation of a random sample from a normal distribution with unknown variance , a confidence interval on is given by ◦ where point of the freedom is the upper distribution with percentage degrees of Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

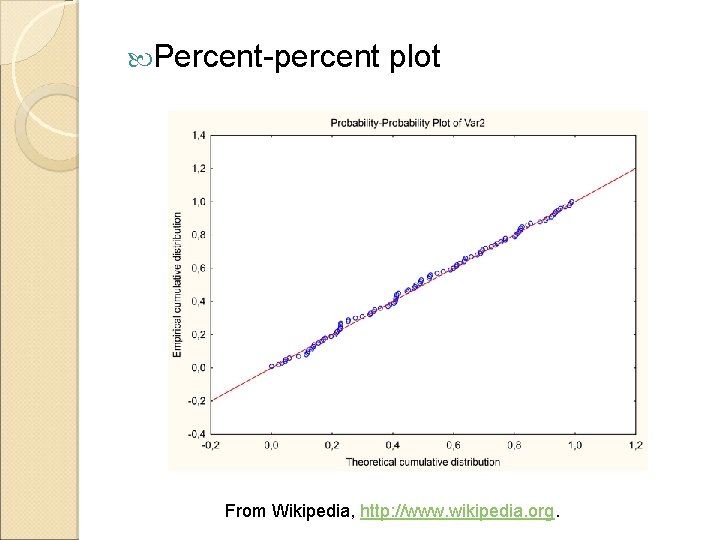
Normal probability plot ◦ The sample , , …, is arranged as , , …, , where is the smallest observation, is the second-smallest observation, and so forth. ◦ The ordered observations are then plotted against their observed cumulative frequency on the appropriate probability paper. ◦ Or, plot the standardized normal scores against , where Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Percent-percent plot From Wikipedia, http: //www. wikipedia. org.

Example 8 -5 Alloy Adhesion ◦ The load at specimen failure: 19. 8, 10. 1, … ◦ , , . ◦ Find a 95% CI on. Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Exercise 8 -41 ◦ An article in Nuclear Engineering International (February 1988, p. 33) describes several characteristics of fuel rods used in a reactor owned by an electric utility in Norway. Measurements on the percentage of enrichment of 12 rods were reported as follows: 2. 94, 3. 00, 2. 90, 2. 75, 3. 00, 2. 95, 2. 90, 2. 75, 2. 95, 2. 82, 2. 81, 3. 05. ◦ (a) Use a normal probability plot to check the normality assumption. ◦ (b) Find a 99% two-sided confidence interval on the mean percentage of enrichment. Are you comfortable with the statement that the mean percentage of enrichment is 2. 95%? Why? Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Confidence Interval on the Variance and Standard Deviation of a Normal Distribution Let , , …, are normally and independently distributed mean and variance , and let be the sample variance. The random variable has a chi-square distribution with

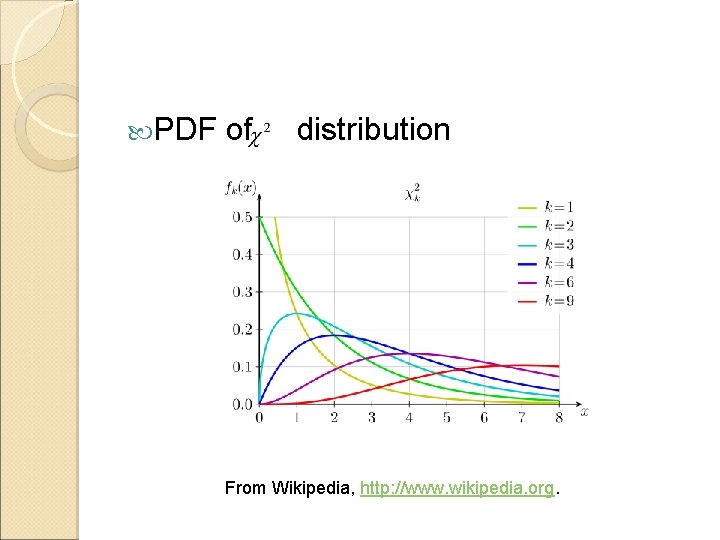
PDF of distribution From Wikipedia, http: //www. wikipedia. org.

CDF of distribution From Wikipedia, http: //www. wikipedia. org.

The probability density function is the number of degrees of freedom Mean : Variance : ◦ Percentage points Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

◦ Since ◦ is chi-square with have degrees of freedom, we Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Confidence interval on the variance ◦ If is the sample variance from a random sample of observations from a normal distribution with unknown variance , then a confidence interval on is ◦ Where and are the upper and lower percentage points of the chi-square distribution with ◦ degrees of freedom, respectively. A confidence interval for has lower and upper limits that are the square roots of the corresponding limits in the above equation Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

One-sided confidence bounds on the variance ◦ The bounds on lower and upper confidence are ◦ respectively. Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Example 8 -6 Detergent Filling ◦ , . ◦ Find a 95% upper confidence bound on. Exercise and 8 -44 ◦ A rivet is to be inserted into a hole. A random sample of parts is selected, and the hole diameter is measured. The sample standard deviation of the hole diameter measurements is millimeters. Construct a 99% lower confidence bound for. Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Large-Sample Confidence Interval for a population proportion Normal approximation for a binomial proportion If is large, the distribution of is approximately standard normal.

PMF of binomial distribution From Wikipedia, http: //www. wikipedia. org.

To construct the confidence interval on , Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

◦ Approximate confidence interval on a binomial proportion If is the proportion of observations in a random sample of size that belongs to a class of interest, an approximate confidence interval on the proportion of the population that belongs to this class is where is the upper percentage of the standard normal distribution. Required: and Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

◦ Sample size for a specified error on a binomial proportion Set Then Or and exercises come from the textbook: Applied Statistics and Contents, figures, Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

◦ Approximate one-sided confidence bounds on a binomial proportion The approximate confidence bounds are lower and upper respectively. Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

◦ Example 8 -7 Crankshaft Bearings , , and Find a 95% two-sided confidence interval for. ◦ Example 8 -8 Crankshaft Bearings How large a sample is required if we want to be 95% confident that the error in using to estimate is less than 0. 05? Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

◦ Exercise 8 -53 The fraction of defective integrated circuits produced in a photolithography process is being studied. A random sample of 350 circuits is tested, revealing 15 defectives. (a) Calculate a 95% two-sided CI on the fraction of defective circuits produced by this particular tool. (b) Calculate a 95% upper confidence bound on the fraction of defective circuits. Contents, figures, and exercises come from the textbook: Applied Statistics and Probability for Engineers, 5 th Edition, by Douglas C. Montgomery, John Wiley &

Tolerance and Prediction Intervals is a single future observation Then has a standard normal distribution and Has a distribution with degrees of freedom.

Prediction A interval prediction interval (PI) on a single future observation from a normal distribution is given by

Tolerance A interval tolerance interval for capturing at least the values in a normal distribution with confidence level is where of is a tolerance interval factor found in Appendix Tabel XII. Values are given for = 90%, 95%, and 99% and for 90%, 95%, and 99% confidence.

Example 8 -9 Alloy Adhesion , , and Find a 95% prediction interval on the load at failure for a new specimen. Example Find 8 -10 Alloy Adhesion a tolerance interval for the load at failure that includes 90% of the values in the population with 95% confidence.

Exercise 8 -77 Consider the rainfall data in Exercise 8 -33. Compute a 95% tolerance interval that has confidence level 95%. Compare the length of the tolerance interval with the length of the 95% CI on the population mean. Discuss the difference in interpretation of these two intervals.