STATISTICS REFRESHER Part 1 2 Agenda Correlation Probability

STATISTICS REFRESHER Part 1 & 2

Agenda • Correlation • Probability Distributions • Independent Events • Binomial Distribution • Normal Distribution • Central Limit Theorem • Confidence Intervals • R Lab

How Things Link Up • We will work with two basic types of data analytics: • Supervised and unsupervised models • Optimizations • Correlation is one of the many ways to understand one of the simplest data models i. e. linear regression • Correlations also play a significant role in determining inputs to models. Remember garbage in – garbage out • Correlations are also very useful in stock portfolio optimizations and overall risk hedging

How Things Link Up • We will work with two basic types of data analytics: • Supervised and unsupervised models • Optimizations • Central limit theorem and hypothesis testing are important in understanding model results • Probability distributions are important when you want to optimize a real world problem because we want to introduce variations in our set up • Some distributions, like normal distribution, are an integral part of the assumptions of many models

Correlation • http: //rpsychologist. com/d 3/correlation/ • Notice the relationship between correlation and shared variance • Measure of association between two variables • Between -1 and 1, with +1 being perfect positive correlation, 0 being no correlation and -1 being perfect negative correlation • Formula: • Why does it work?

Correlation • Imagine two sets of 10 numbers each, the aim is to rearrange the sets such that their sum product or dot product is maximized. How do we do that?

Correlation • Imagine two sets of 10 numbers each, the aim is to rearrange the sets such that their sum product or dot product is maximized. How do we do that? • Does the solution from above allow us to compare between different sets of numbers? If not, how can we fix that?

Probability Distributions • A probability distribution is a function that describes the likelihood of obtaining the possible values that a random variable can assume • For example: if I toss a coin twice, I can obtain 0 or 1 or 2 heads; the random variable “X” = No. of heads obtained can be modeled as follows: X 0 1 2 P(X = x) 0. 25 P(X <= x) 0. 25 0. 75 1 • Point probabilities are given by a PDF, cumulative probabilities by a CDF

Probability Distributions • Two different kinds of distributions: discrete and continuous • What is the probability of a continuous distribution at a point X = a? • How can we calculate the mean and variance of a discrete random variable if we know the probability distribution?

Probability Distributions • Two different kinds of distributions: discrete and continuous • How can we calculate the mean (aka expected value) and variance of a discrete random variable if we know the probability distribution? • Formula: • What is the probability of a continuous distribution at a point X = a?

Probability Distributions • Two different kinds of distributions: discrete and continuous • How can we calculate the mean (aka expected value) and variance of a discrete random variable if we know the probability distribution? • Formula: • What is the probability of a continuous distribution at a point X = a? • Can we use a proxy for point probabilities in continuous distributions?

Binomial Distribution • Useful for cases where the experiment result is binary in each attempt e. g. tossing a coin has only two results • Sale – no sale on a lead is also an example of activity that can be modeled binomially • We assume individual trails/events are independent • What is the meaning of independent events? • P(A|B) = P(A) • P(A & B) = P(A) * P(B) • Why is it important to know whether events are independent? • Lets assume there are two hospitals – hospital A treated 510/650 patients successfully. Hospital B treated 340/650 successfully. Which hospital is better?

Independent Events • For a binomial distribution (as well as all other commonly used distributions) we assume that individual trials/events are independent • What is the meaning of independent events? • P(A|B) = P(A) • P(A & B) = P(A) * P(B) • Why is it important to know whether events are independent? • Lets assume there are two hospitals – hospital A treated 510/650 patients successfully. Hospital B treated 340/650 successfully. Which hospital is better?

Independent Events • Does the table below change your decision? Why? Hospital A Hospital B Treated Failed Serious Case 10 90 200 300 Normal Case 500 50 140 10 Total 510 140 310 • In this example event A i. e. patient is successfully treated is not independent from event B i. e. patient reported a serious illness • For hospital A: P(success | serious) = 10/100 or 10% while P(success) = 510/650 = 78% • For hospital B: P(success | serious) = 200 / 500 or 40% while P(success) = 340/650 = 52%

Binomial Distribution • We just observed how dependent events can behave differently from independent events • Since independent events allow us to carry forward the same assumptions (for e. g. P(success) in a coin toss) to the next trial, they allow crucial simplifications needed for ease of work • For a binomial distribution, only two parameters are of interest: • Number of trials • P(Success) on a trial; assuming independence, this will not change from trial to trial

Binomial Distribution

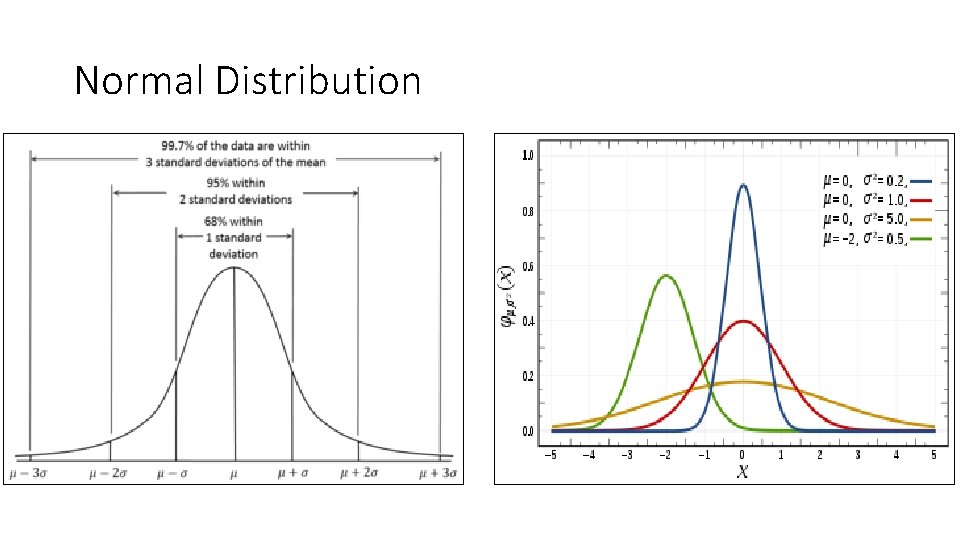
Normal Distribution

Normal Distribution • Normal table provides cumulative probability i. e. P(X <= x) • Excel provides the PDF and CDF with the NORM. DIST function • If we want to read from the normal distribution table, we must standardize our X to have mean 0 and standard deviation 1. This is done by the following formula: • Question: Given some data, how do we know if a variable follows a normal distribution?

Central Limit Theorem • What is the distribution for a single dice roll? • What is the distribution for the sum of two dice rolls? What about the mean of two dice rolls? • What is the distribution for the sum of three dice rolls? What about the mean of three dice rolls?

Central Limit Theorem • Given any population distribution, the sampling distribution formed by taking the mean of multiple random samples will always follow a normal distribution • The mean of the sampling distribution will be distributed around population mean µ • The standard deviation of the sampling distribution, also known as standard error, will reduce by a factor of 1/sqrt(N) • Why is this important? What role does it play in confidence intervals and hypothesis testing?

Confidence Intervals • Given that the central limit theorem yields a normal distribution as discussed in the previous slide, can we use a sample and the properties of a normal distribution to make a claim about the population? • Using the 68 -95 -99 rule, can we make a statement between the relationship of the sample mean and population mean? • http: //rpsychologist. com/d 3/CI/