Statistics Quantitative Methods 1 The normal distribution can

Statistics Quantitative Methods

1. The normal distribution can be defined by its mean and ____. A. B. C. D. mode median standard deviation skewness

1. The normal distribution can be defined by its mean and ____. A. B. C. D. mode median standard deviation skewness

2. The normal distribution is also called the symmetrical, Gaussian or ____ distribution. A. skewed B. bi-modal C. bell-shaped D. point-biserial

2. The normal distribution is also called the symmetrical, Gaussian or ____ distribution. A. skewed B. bi-modal C. bell-shaped D. point-biserial E. all of the above

3. Scores far from the mean are located in the ____ of a normal distribution. A. B. C. D. body tails most sensitive areas most uncertain areas

3. Scores far from the mean are located in the ____ of a normal distribution. A. B. C. D. body tails most sensitive areas most uncertain areas

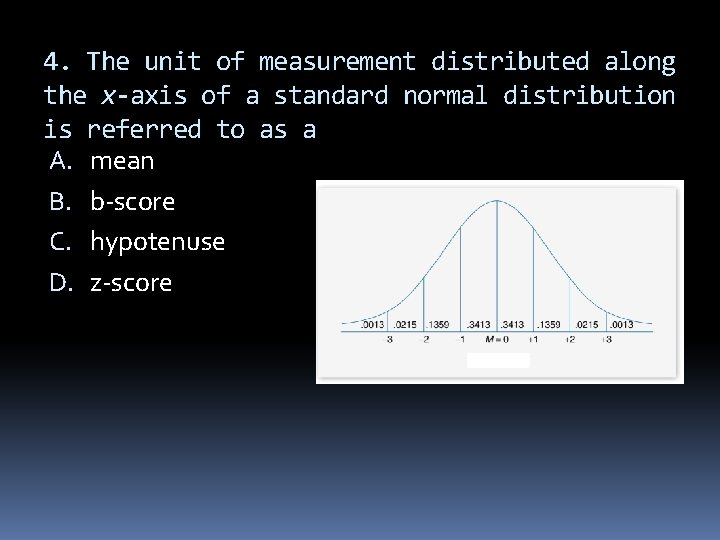
4. The unit of measurement distributed along the x-axis of a standard normal distribution is referred to as a A. mean B. b-score C. hypotenuse D. z-score

4. The unit of measurement distributed along the x-axis of a standard normal distribution is referred to as a A. mean B. b-score C. hypotenuse D. z-score

5. A researcher finds that the average preschool-aged child drinks two cups of milk per day. Assuming these data are normally distributed, the z-score for the average cups per day in this example is A. B. C. D. less than 0 greater than 0 exactly equal to 0 There is not enough information to answer this question.

5. A researcher finds that the average preschool-aged child drinks two cups of milk per day. Assuming these data are normally distributed, the z-score for the average cups per day in this example is A. B. C. D. less than 0 greater than 0 exactly equal to 0 There is not enough information to answer this question.

6. Which of the following is required to locate proportions of area under the normal curve? A. Compute a ztransformation. B. Find the probability of a z-score in the unit normal table. C. both A and B D. none of the above

6. Which of the following is required to locate proportions of area under the normal curve? A. Compute a ztransformation. B. Find the probability of a z-score in the unit normal table. C. both A and B D. none of the above

7. For a normally distributed sample of scores with a mean of 8 and standard deviation of 2 what is the z-score for a raw score of 12? A. 0 B. 2 C. 4 D. 6

7. For a normally distributed sample of scores with a mean of 8 and standard deviation of 2 what is the z-score for a raw score of 12? A. B. C. D. 0 2 4 6

8. What percent of raw scores fall below the mean? A. B. C. D. 25% 50% 75% 100%

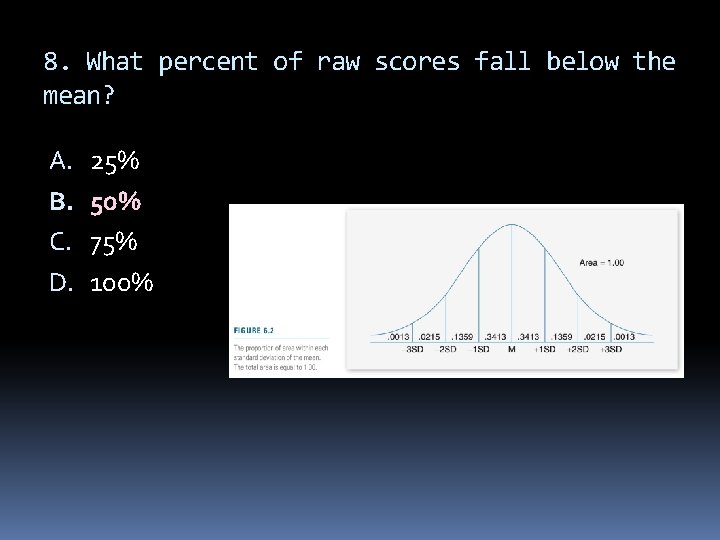
8. What percent of raw scores fall below the mean? A. B. C. D. 25% 50% 75% 100%

9. For a normally distributed sample of scores with a mean of 8 and standard deviation of 2, what z score corresponds to a raw score of 6? A. B. C. D. -1. 0 +1. o +6. 0 -6. 0

9. For a normally distributed sample of scores with a mean of 8 and standard deviation of 2, what z score corresponds to a raw score of 6? A. B. C. D. -1. 0 +1. o +6. 0 -6. 0

10. For a normally distributed sample of scores with a mean of 8 and standard deviation of 2, what score corresponds to a z-score of +1. 0 ? A. B. C. D. 2 4 10 8

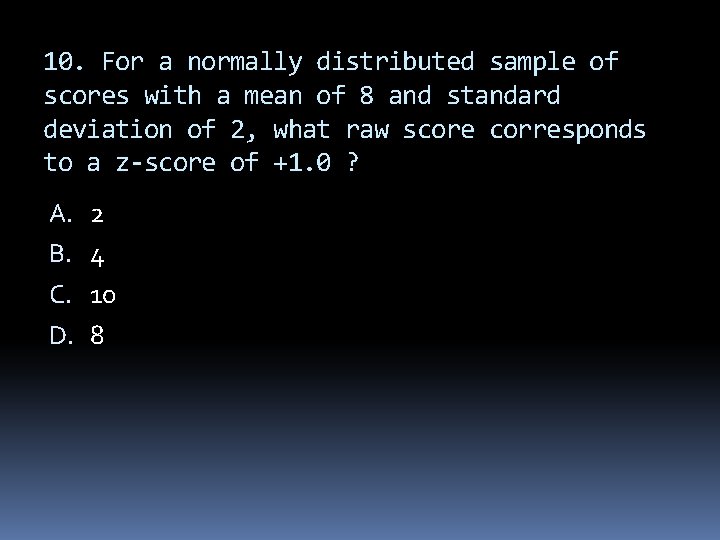
10. For a normally distributed sample of scores with a mean of 8 and standard deviation of 2, what raw score corresponds to a z-score of +1. 0 ? A. B. C. D. 2 4 10 8

The End