Statistics Primer Xiayu Stacy Huang Bioinformatics Shared Resource

Statistics Primer Xiayu (Stacy) Huang Bioinformatics Shared Resource Email: bsr_help@sanfordburnham. org Sanford | Burnham Medical Research Institute

Outline § Overview of basic statistics Introduction Descriptive statistics Inferential statistics § Most common statistical test and its applications T test Power analysis using t test

What is statistics? On American Statistical Association (ASA) website, statistics is defined as the science of collection, analysis, interpretation and presentation of data Using Statistics to make decision can be a double-edged sword In the 1980 s, Marriott conducted an extensive survey with potential customers on their attitudes about current hotel offerings. After analyzing the data, the company launched Courtyard by Marriott, which has been a huge success Coca-Cola performed a major consumer study in 1985 and, based on the results, decided to reformulate Coke, its flagship drink. After a huge public outcry, Coca-Cola had to backtrack and bring the original formulation back to market

History of statistics • 17 th-18 th century • Bernoulli number • Bernoulli trial • Bernoulli process Jakob Bernoulli • Bayes theorem Thomas Bayes • 19 th century • Gaussian distribution Carl Friedrich Gauss • 20 th century Karl Pearson William Gosset • Pearson correlation • Chi-square distribution • Student’s t Ronald Aylmer Fisher • ANOVA, maximum likelihood

Why statistics is important to biologists? • Designing experiment How many ? ? ? How many replicates for my microarray exp? ? ? • Analyzing biological data and understanding analysis results Identifying outlier Normalization/transformation Statistical test, etc. DEGs No replicates=No statistics? • Preparing manuscript and grant applications
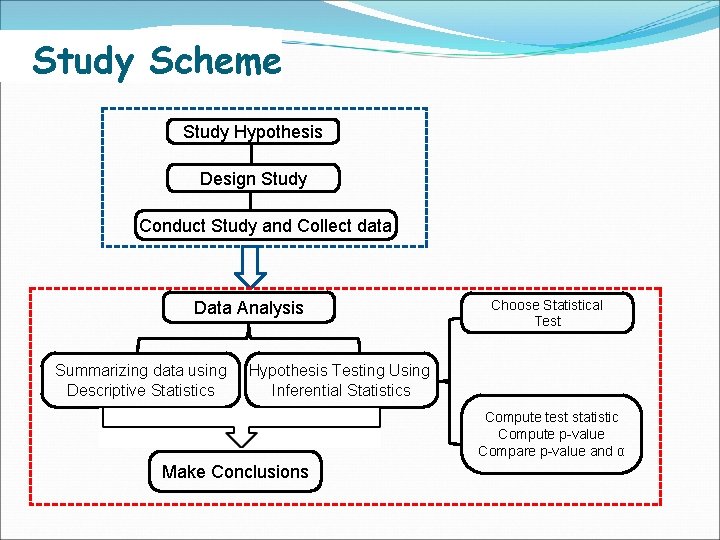
Study Scheme Study Hypothesis Design Study Conduct Study and Collect data Data Analysis Summarizing data using Descriptive Statistics Choose Statistical Test Hypothesis Testing Using Inferential Statistics Compute test statistic Compute p-value Compare p-value and α Make Conclusions

Branches of statistics Descriptive statistics (Summary statistics) Summarize data graphically or numerically Lead to hypothesis generating Inferential statistics Distinguish true difference from random variation Allow hypothesis testing

Types of data Qualitative or Quantitative Example Qualitative Gender Genotype Tumor location Qualitative or Quantitative Performance Grade of tox Disease stage Quantitative Age Array intensities
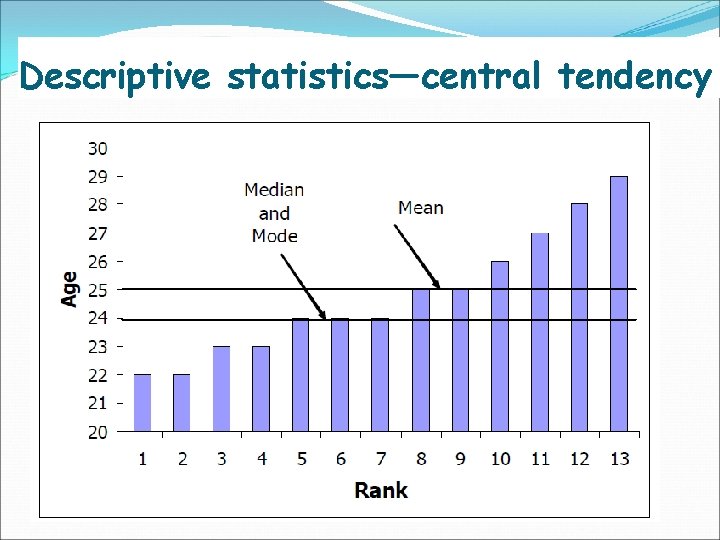
Descriptive statistics—central tendency § Mean—average i. e. Age 24 27 22 25 24 23 28 23 25 26 22 29 24 25 26 27 28 29 Mean=(24+27+…. +24)/13=24. 8 § Median—middle value of sorted data 22 22 23 23 24 24 24 25 Median § Mode—most frequently observed value Mode is 24 with frequency of 3
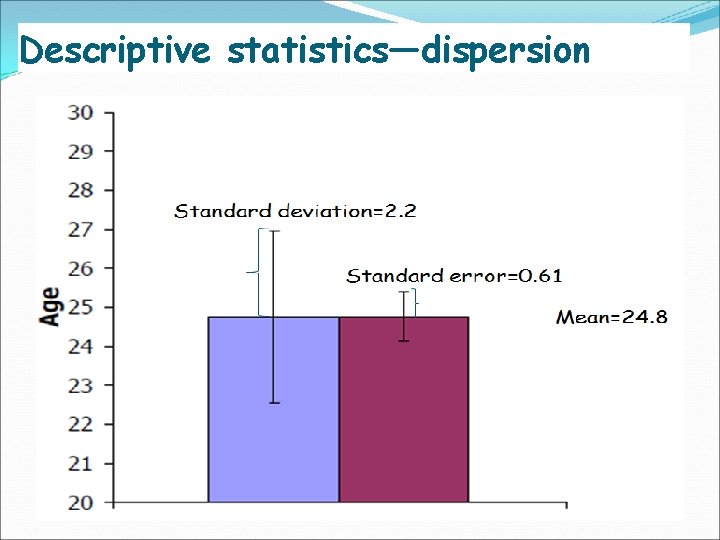
Descriptive statistics—dispersion Range i. e. Age 22 22 23 23 24 24 24 25 25 26 27 28 29 Range=highest value-lowest value=29 -22=7 Sample Variance (s 2) Standard deviation (s) Values beyond two standard deviations from the mean can be considered as “outliers” (>mean+2 s=24. 8+2 x 2. 2=29. 2 or <mean-2 s=24. 8 -2 x 2. 2=20. 4) Standard error of mean (SEM)
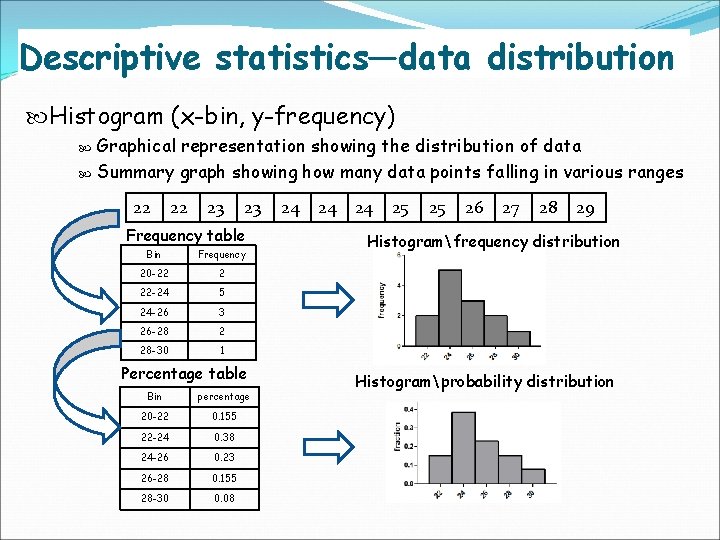
Descriptive statistics—data distribution Histogram (x-bin, y-frequency) Graphical representation showing the distribution of data Summary graph showing how many data points falling in various ranges 22 22 23 23 Frequency table Bin Frequency 20 -22 2 22 -24 5 24 -26 3 26 -28 2 28 -30 1 Percentage table Bin percentage 20 -22 0. 155 22 -24 0. 38 24 -26 0. 23 26 -28 0. 155 28 -30 0. 08 24 24 24 25 25 26 27 28 29 Histogramfrequency distribution Histogramprobability distribution
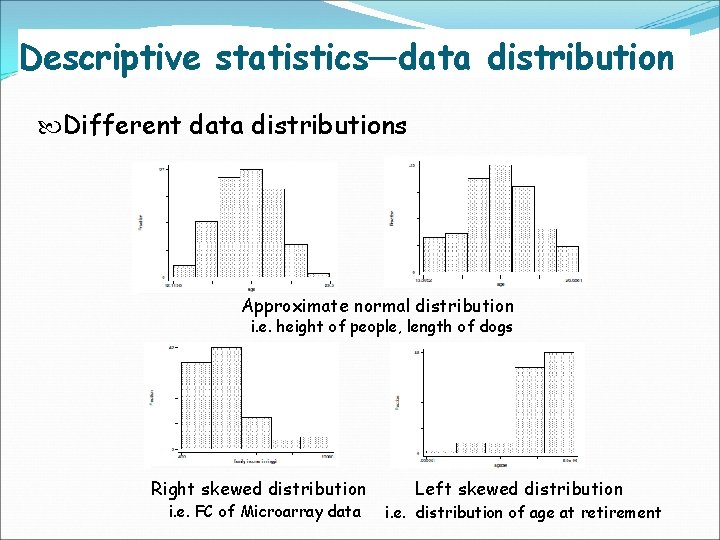
Descriptive statistics—data distribution Different data distributions Approximate normal distribution i. e. height of people, length of dogs Right skewed distribution i. e. FC of Microarray data Left skewed distribution i. e. distribution of age at retirement

Normal (or Gaussian) distribution mean=median=mode • Bell-shaped curve • Symmetrical about mean • Mean, median and mode are equal • ~68% data points fall within 1 sd of mean • ~95% data points fall within 2 sd of mean • ~99. 7% data points fall within 3 sd of mean

Installing graphpad prism You can install Prism on Institute supplied computers, including home and personal computers. http: //graphpad. com/paasl/index. cfm? sitecode=burnhm SERIAL NUMBERS: Macintosh version contacting IT (support@sanfordburnham. org) to get serial number Windows version contacting IT (support@sanfordburnham. org) to get serial number
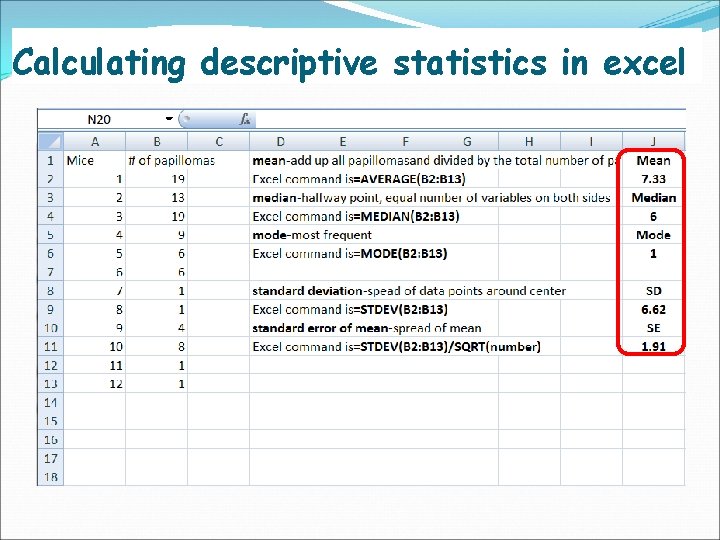
Calculating descriptive statistics in excel
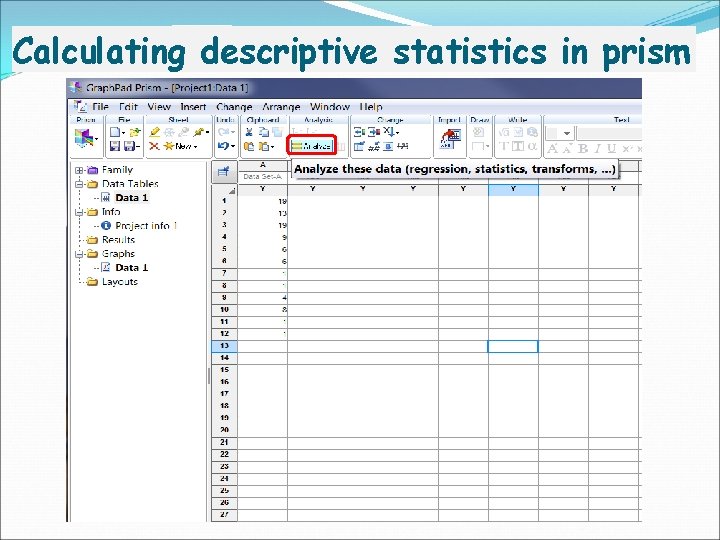
Calculating descriptive statistics in prism
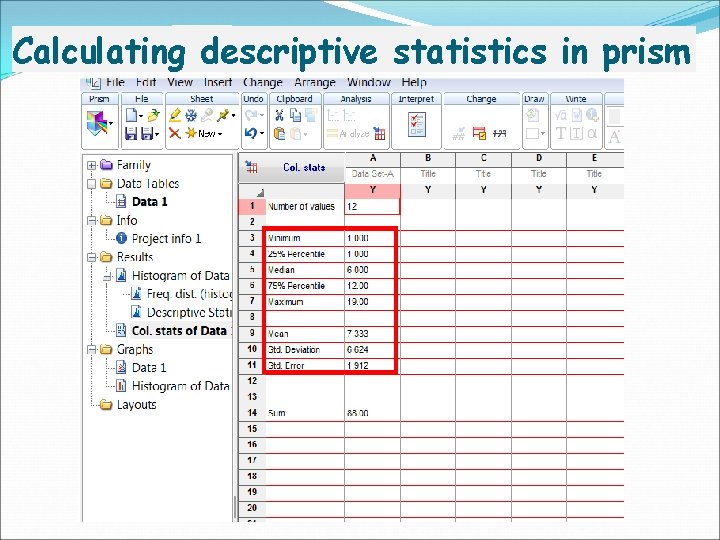
Calculating descriptive statistics in prism
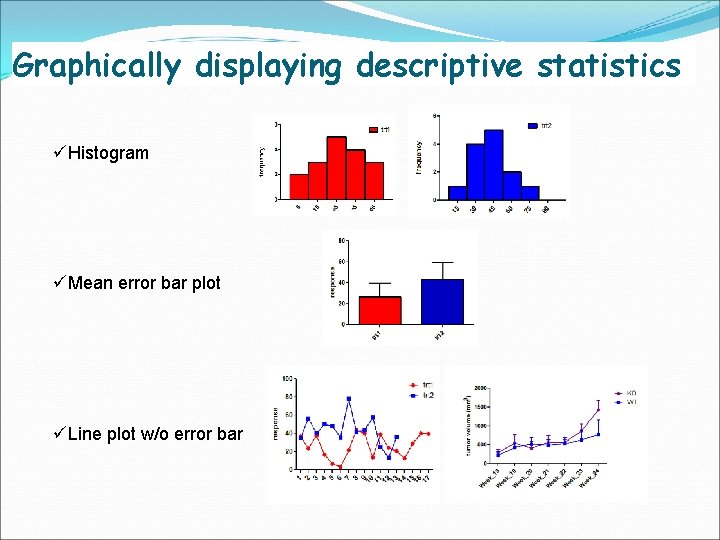
Graphically displaying descriptive statistics üHistogram üMean error bar plot üLine plot w/o error bar
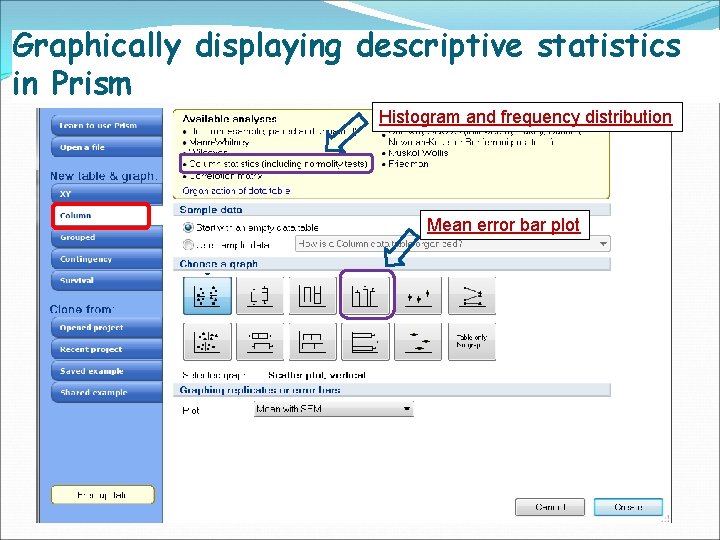
Graphically displaying descriptive statistics in Prism Histogram and frequency distribution Mean error bar plot
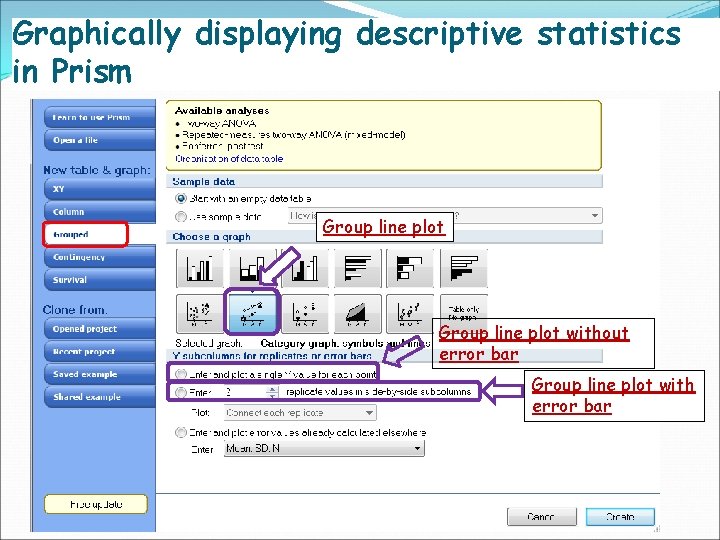
Graphically displaying descriptive statistics in Prism Group line plot without error bar Group line plot with error bar
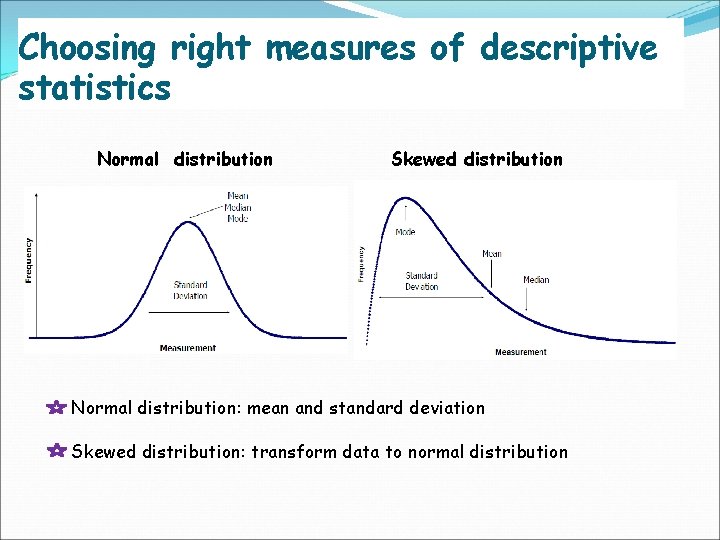
Choosing right measures of descriptive statistics Normal distribution Skewed distribution Normal distribution: mean and standard deviation Skewed distribution: transform data to normal distribution

Outline § Overview of basic statistics Brief Introduction Descriptive statistics Inferential statistics § Most common statistical tests and its applications T test Power analysis using t test

Inferential statistics Parametric Interval or ratio measurements Continuous variable Usually assuming data are normally distributed Nonparametric Ordinal or nominal measurements Discreet variables Making no assumption about how data is distributed

Inferential statistics-hypothesis Null hypothesis (H 0) new drug effect = old drug effect tumor growth of MT = tumor growth of WT Alternative hypothesis (HA) • • is the opposite of null hypothesis is generally the hypothesis that is believed to be true by the researcher new drug effect ≠ or > old drug effect tumor growth of MT ≠ or < tumor growth of WT

Inferential statistics-one and two sided tests Hypothesis tests can be one or two sided (tailed) One sided tests are directional: H 0 : new drug effect ≤ old drug effect HA : new drug effect > old drug effect Two sided tests are not directional: H 0 : new drug effect = old drug effect HA : new drug effect ≠ old drug effect
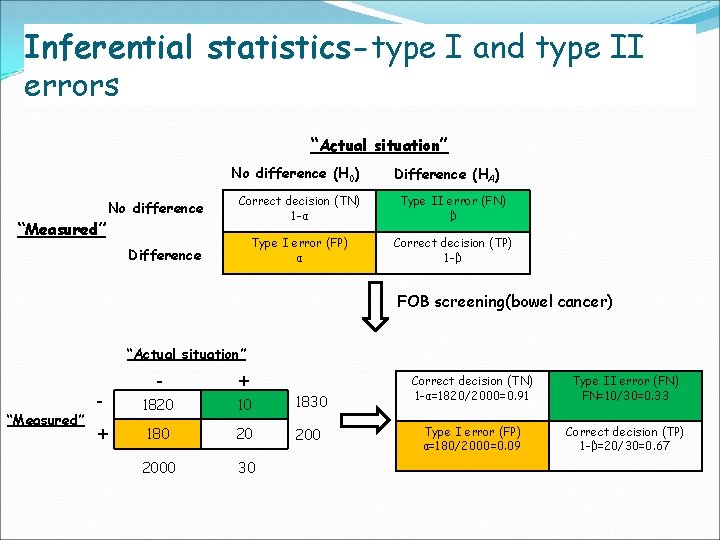
Inferential statistics-type I and type II errors “Actual situation” No difference (H 0) No difference “Measured” Difference (HA) Correct decision (TN) 1 -α Type II error (FN) β Type I error (FP) α Correct decision (TP) 1 -β Difference FOB screening(bowel cancer) “Actual situation” “Measured” - - + 1820 10 1830 + 180 20 2000 30 Correct decision (TN) 1 -α=1820/2000=0. 91 Type II error (FN) FN=10/30=0. 33 Type I error (FP) α=180/2000=0. 09 Correct decision (TP) 1 -β=20/30=0. 67

Inferential statistics-type I and type II errors • Control type I and type II errors • Inverse relationship between type I and type II errors • Make a choice to control which error • i. e. controlling type I error (FP) is more important for microarray data than type II error (FN) • i. e. controlling type II error (FN) is more important for cancer screening test than type I error (FP) • Choose type I and type II errors for statistical test? • Common choices (α = 5%, β = 20%) • Exploratory study (α = 10%, β = 10%) • Confirmatory study (α = 1%, β = 10%)

Inferential Statistics-P-value • the probability that an observed difference could have occurred by chance under null hypothesis • Computed from test statistics score • P-value is the same as false positive rate • P-value below cut off (α) is referred as “statistically significant”

Inferential Statistics-Power (1 -β, aka true positive rate (TP)) • Probability of detecting a significant scientific difference when it does exist Power depends on: Sample size (n) Standard deviation (s) Size of the difference you want to detect (δ) False positive rate (α) Effect size
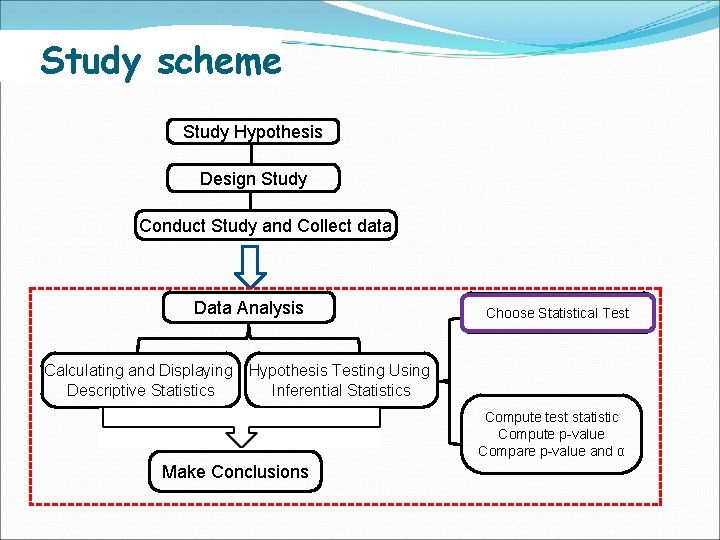
Study scheme Study Hypothesis Design Study Conduct Study and Collect data Data Analysis Choose Statistical Test Calculating and Displaying Hypothesis Testing Using Descriptive Statistics Inferential Statistics Compute test statistic Compute p-value Compare p-value and α Make Conclusions

How to choose an appropriate statistical test? Type of data Quantitative Qualitative Type of research question Association Correlation Comparison Data structure Independent Paired Matched
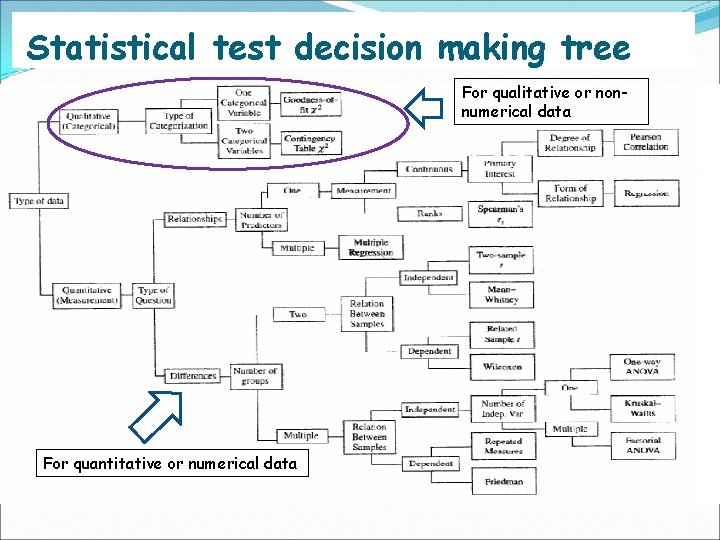
Statistical test decision making tree For qualitative or nonnumerical data For quantitative or numerical data
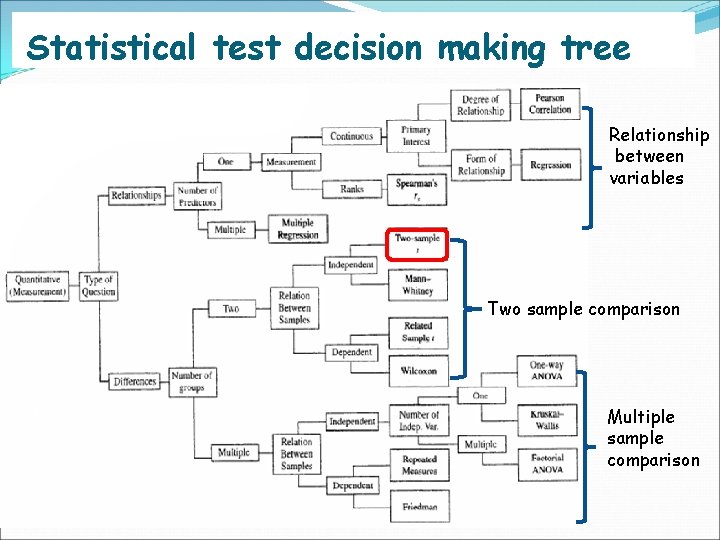
Statistical test decision making tree Relationship between variables Two sample comparison Multiple sample comparison

Outline § Overview of basic statistics Brief Introduction Descriptive statistics Inferential statistics § Most common statistical test and its applications T test Power analysis using t test

Student’s t test Guinness employee William Sealy Gosset published the 'Student's t-test' in 1908

Types of t test One sample t test: test if a sample mean differs significantly from the given known mean Unpaired t test: test if two independent sample means differ significantly Paired t test: test if two dependent sample means differ significantly (mean of pre and post treatment for same set of patients

Application of t test in biology Mincroarry experiment WT MT Proteomics experiment WT MT Biological reps Technical reps ØYou need to have at least two replicates in each condition to do t test, otherwise, t test is invalid and you won’t have statistics

Two sample unpaired t test Assumptions Data is approximately normally distributed The sample has been independently and randomly selected Similar variances between comparing groups Hypothesis (two sided or one sided) Test statistics -- sample means -- population means -- sample standard deviation -- sample size -- pooled sample variance
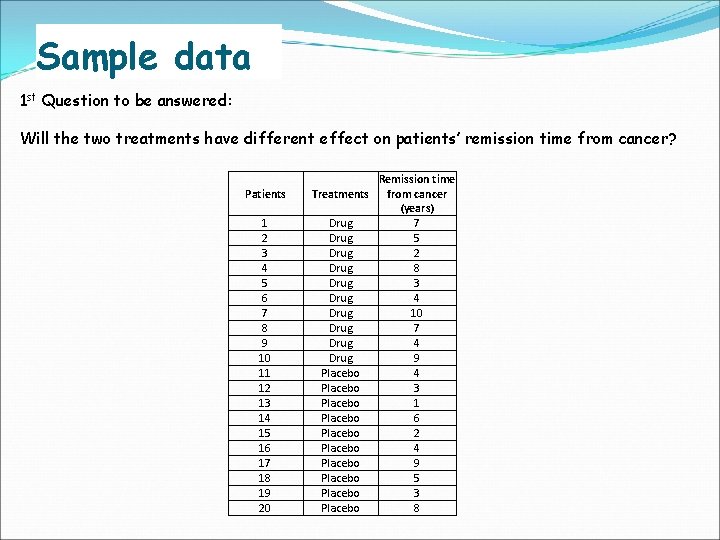
Sample data 1 st Question to be answered: Will the two treatments have different effect on patients’ remission time from cancer? Patients 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Remission time Treatments from cancer (years) Drug 7 Drug 5 Drug 2 Drug 8 Drug 3 Drug 4 Drug 10 Drug 7 Drug 4 Drug 9 Placebo 4 Placebo 3 Placebo 1 Placebo 6 Placebo 2 Placebo 4 Placebo 9 Placebo 5 Placebo 3 Placebo 8
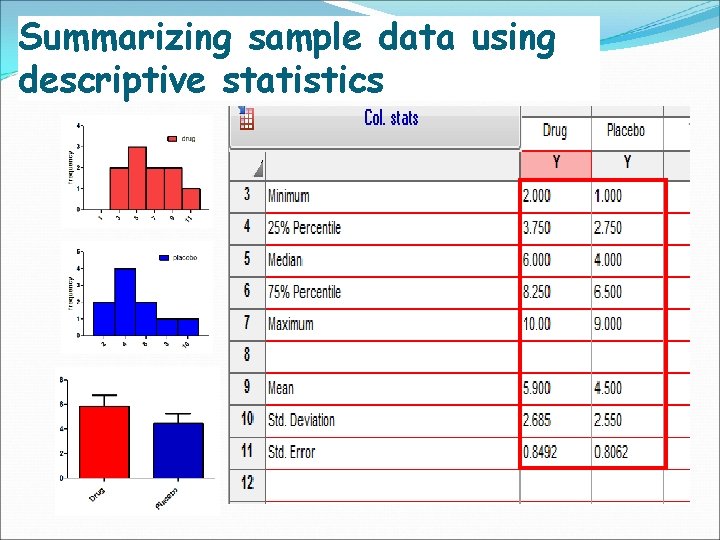
Summarizing sample data using descriptive statistics

Hypothesis testing of sample data using inferential statistics Step 1: Choosing an appropriate statistical test Step 2: Performing statistical test in software Step 3: Making conclusions
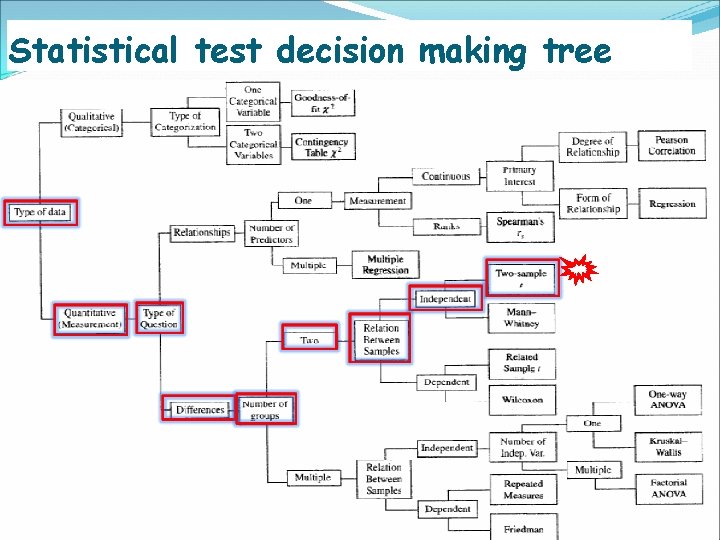
Statistical test decision making tree
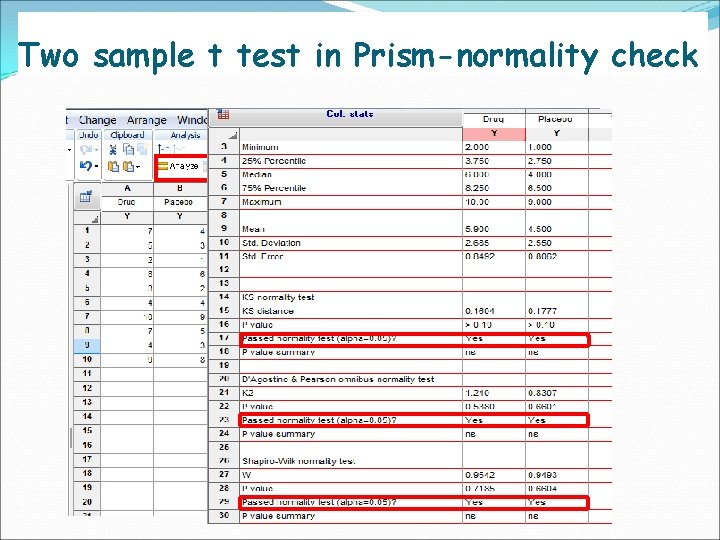
Two sample t test in Prism-normality check
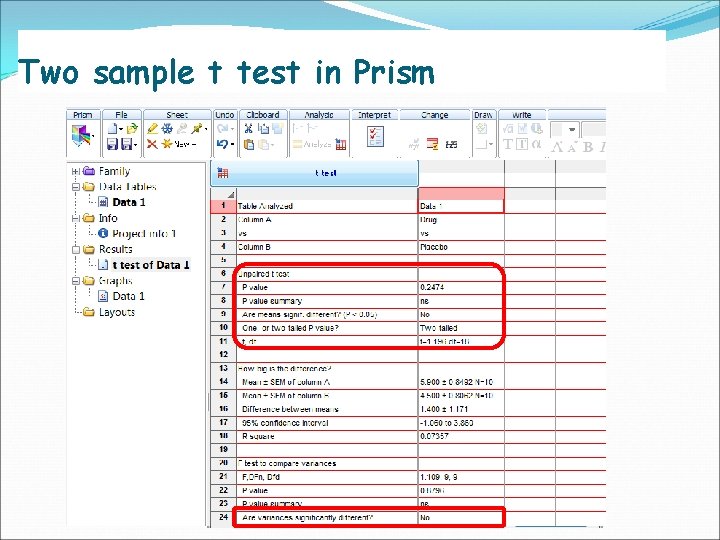
Two sample t test in Prism
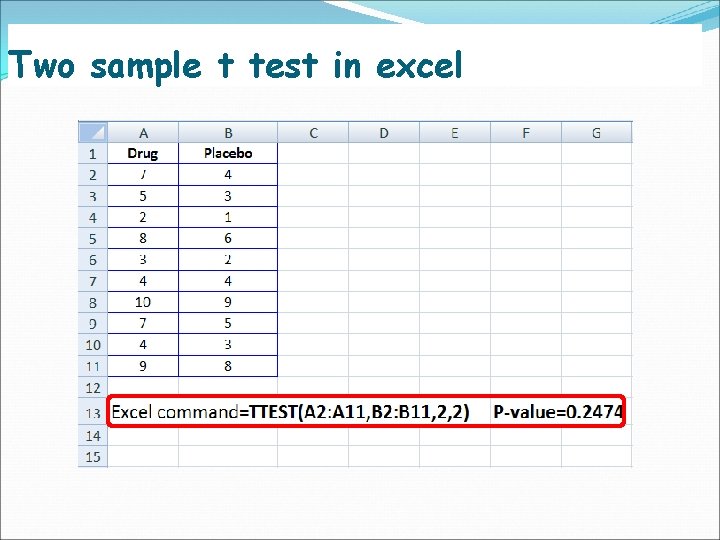
Two sample t test in excel

Power analysis using two sample t test 2 nd question to be answered: How many patients do we need in order to detect a significantly difference b/w two treatments? N α β δ/s Test efficiency K: 1 imbalance
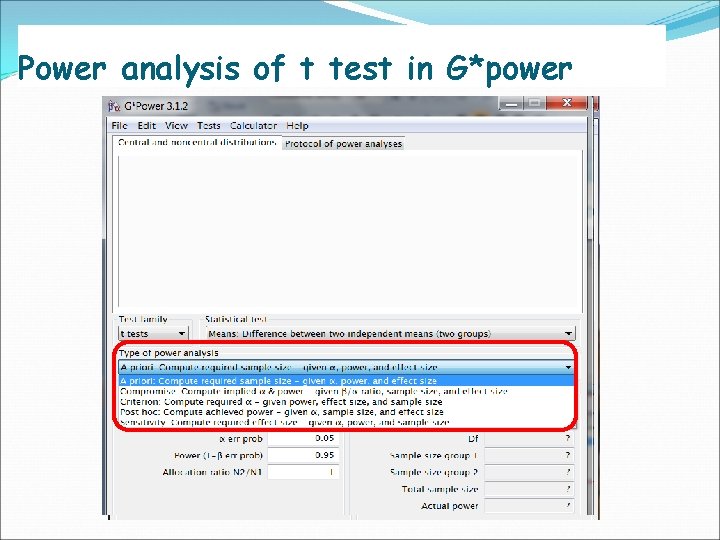
Power analysis of t test in G*power
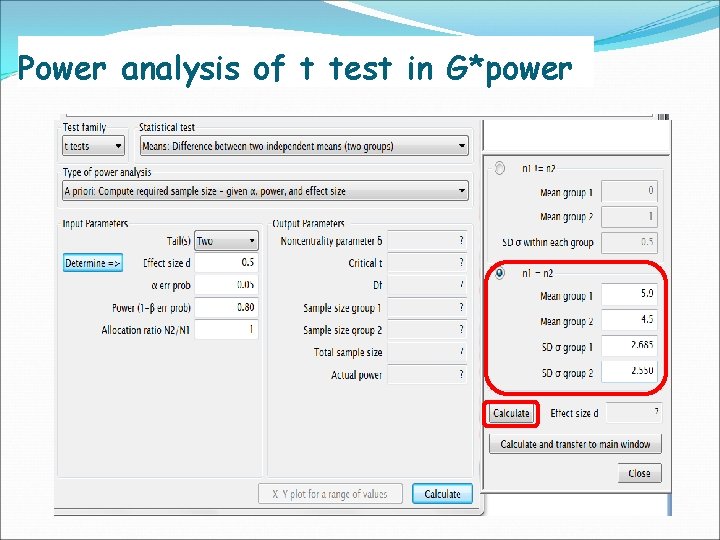
Power analysis of t test in G*power

Basic Statistics tools Statistics softwares and packages: 1. Excel and add-ins: EZAnalyze, Analysis Toolpak 2. Our institute supported Prism 3. SPSS, Statistica (commercial) 4. SAS (commercial) and R 5. G*Power Basic statistics books: 1. Intro Stats, SDSU, 2 nd edition, Deveaux, Velleman, Bock 2. Choosing and Using Statistics: A Biologist's Guide 3. Introduction to Statistics for Biology 4. Biostatistical analysis, fifth edition, Jerrold H. Zar Statistics videos: 1. http: //www. microbiologybytes. com/maths/videos 2. http: //www. youtube. com: descriptive statistics, basic statistics, install 2007 Excel data analysis add-ins…

Next. . . My presentation will be posted on website: http: //bsrweb. burnham. org/ I am located in building 10, Office 2405, ext 3916 Feel free to come or call or send e-mail to ask questions (xyhuang@sanfordburnham. org) Group email: bsr_help@sanfordburnham. org
- Slides: 50