Statistics Part II Math 416 Game Plan n

Statistics Part II Math 416

Game Plan n Creating Quintile n Decipher Quintile n Per Centile Creation n Per Centile Interpretation n Statistical Interpretation

Quintiles n We have looked at quartiles where we divide the data into quarters to look at the “spread” of data n Now we will be looking at dividing the data into fifths n We are now concerned with the position of data n Eg The data in the group is very concentrated.

Quintiles We call n First R 1 n Second R 2 n Third R 3 n Fourth R 4 n Fifth R 5 n The top / best The bottom / worst Report Card Handout To divide data into fifths there are certain guidelines not rules that need to be followed.

Creating Quintiles n 1) The data must be in order (this can be a pain!) n 2) Roughly divide them into fifths called the 1 st try n * 3) Keep numbers the same together n * 4) Keep the groups the same size n * 5) keep number close together

Creating Quintiles Guidelines #3, 4, &5 probably #3 is the most important n Realize that these are guidelines you may need to with a sample of 30 points make decisions that could be different from me R 3 R 995 5 Does 5 n The other factor is size of sample R 8 R 1005 4 not n If you have 4 a sample of 5000 & you move Itneed cantolook R 3 6 several points… R 3 1000 look unbalanced R 2 5 R 2 990 bad R 1 8 R 1 1010 n

Practice n Below are a set of numbers… put them into quintiles n (32, 43, 47, 44, 45, 31, 39, 32, 49 44, 40, 49, 36, 49, 48, 40, 41, 43, 44, 43, 39, 36, 33, 55, 50, 38, 31, 45) n 1 st step – get them in order!

Quintiles n In order… 31, (31, 32, 33, 36, 38, 39, 39, 40, 40, 41, 43, 43, 44, 44, 45, 47, 48, 49, 49, 50, 55) 2 nd step: n 1 st try through… 31, 32, 33, 36 * 36, 38, 39, 39, 40 * 40, 41, 43, 43 44, 44, 45 * 45, 47, 48, 49, 49, 50, 55 n

Quintiles R 5 31, 32, 33, 36 n R 4 38, 39, 39, 40, 40 MY n R 3 41, 43, 43 QUINTILES n R 2 44, 44, 44 n R 1 45, 47, 48, 49, 49, 50, 55 n

Interpretation of Quintiles Basically, since we need to rank data from best to worst we create a hierarchy n Be careful – statistics do not create good and bad n The Quintile Range n We sometimes only look at the endpoints of the quintile n Thus Rx [8, 41] means all the numbers from 8 to 41 including 8 and 41. n

Example n n n n n A class has the following quintile structure R 5 [40, 50] R 4 [51, 60] R 3 [61, 75] R 2 [76, 90] R 1 [90, 99] What do you notice about this class? The class has students close to the bottom and top and a wide spread in middle (teacher’s nightmare) If Billy has a mark of 81, where would he fit in? Into the second quintile

Percentiles If dividing data into four was fun and five was more fun, let’s try 100! n If we say there are n data points and we are trying to figure out the percentile, the formula is n P Billy = (number below + ½ number equal) x 100 n or n Px = NB + ½ NE x 100 n n

Example #1 Consider 6, 9, 15, 23, 27, 29, 41, 52, 58) n What is P 24 ? n P 24 = NB + ½ NE x 100 n n P 24 = 4 + ½ (0) x 100 9 n P 24 = 44 n This means that 24 is in the 44 th percentile and that 44% of the scores fall below n

Example #2 Consider (5, 9, 9, 18, 23, 24, 24, 61, 63, 65) n What is P 24 ? n P 24 = NB + ½ NE x 100 n n n P 24 = 5+ ½ (3) x 100 n 11 n P 24 = 59 n

Example #3 Consider (6, 9, 11, 12, 14, 18, 22, 28, 29) n Where does the 63 rd percentile begin? n We use the formula BVP = n (Px) (Beginning Value Position) 100 n BVP = 9 x 63 100 n BVP = 5. 67 ; Thus we need 5 below n Therefore, 18 is where the 63 rd percentile begins n Note: These are calculations; the size of the sample make them at best approximation n

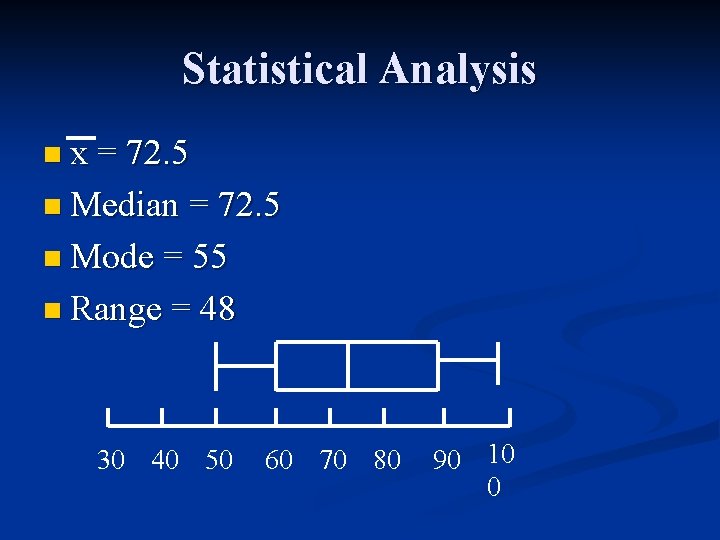
Statistical Analysis You need to see what all these techniques mean. Let’s put it all together… n For the following data find the a) mean b) median c) mode d) range e) box and whisker and f) quintile range (50, 55, 55, 55, 60, 62, 63, 65, 67, 70, 72, 73, 74, 75, 76, 77, 78, 80, 89, 90, 90, 91, 93, 95, 98) n = 30 n

Statistical Analysis n x = 72. 5 n Median = 72. 5 n Mode = 55 n Range = 48 30 40 50 60 70 80 90 10 0

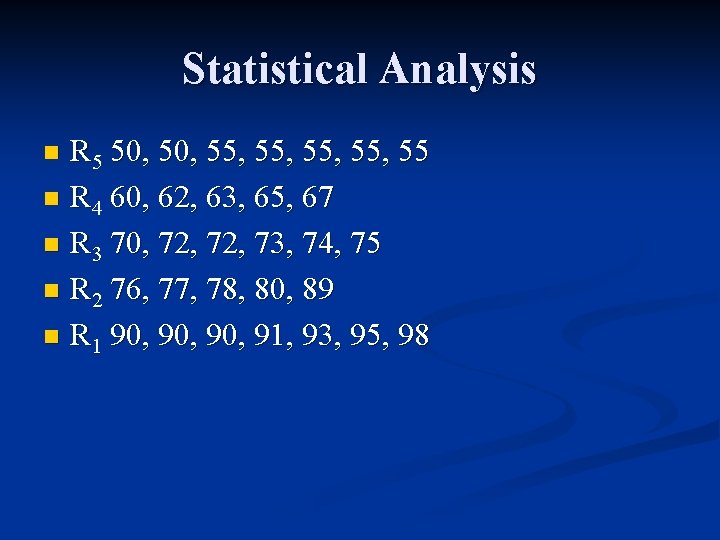
Statistical Analysis 1 st try 50, 55, 55, 55 * 55, 60, 62, 63, 65, 67 70, 72, 73, 74, 75 76, 77, 78, 80, 89, 90 * 90, 91, 93, 95, 98 n

Statistical Analysis R 5 50, 55, 55, 55 n R 4 60, 62, 63, 65, 67 n R 3 70, 72, 73, 74, 75 n R 2 76, 77, 78, 80, 89 n R 1 90, 90, 91, 93, 95, 98 n

Statistical Analysis The mean and the median close together means it is pretty normal n The mode being very different may be a problem n R = 48 n = 30 look at 48 / 30 = 1. 6 (small spread) n Box & Whisker looks pretty normal (same size box) n Quintiles worked out pretty normal n Overall nothing spectacular n

Strange Things You May Encouter n n n n n X = 50; Median = 12… something funny R = 100 n = 3 100 / 3 = 33 big spread! Box and Whisker will have a very large box with the above… not normal Consider Quintiles R 5 = 17 R 4 = 10 R 3 = 16 R 2 = 4 R 1 = 20 Big difference; something funny

Final Word Try to live by “statistics never lie – so do not make them” n Avoid making definite statement (it is) n Use words like seem like, appears to be… n The teacher is bad because the class average is low… is a definite statement and should be rephrased n Good luck and study hard! n