STATISTICS NETWORKING DAY Species Distribution Models SDM for

STATISTICS NETWORKING DAY Species Distribution Models (SDM) for Presence Only (PO) data. Maria Angelica Lopez-Aldana Principal Supervisor: Assoc. Prof. Bernd Gruber Associate Supervisor: Dr. Carlos Gonzalez-Orozco Prof. Arthur Georges August 2015 MDBfutures Collaborative Research Network 1

MDBfutures Collaborative Research Network Outline • An overview about Species Distribution Models (SDM) • SDM methods • SDM for presence only (PO) data. • Learning resources. • Complexities and recommendations.

MDBfutures Collaborative Research Network An overview about Species Distribution Models (SDM) Ecological question: What is the species occurrence probability on a determined area? Uses: - Reserve design and conservation planning. - Target areas for protected status. - Assess threats to protected areas - Design reserves - Ecological restoration Risk and Impacts of Invasive Species. Effects of global warming on biodiversity. Describing or estimating macroecological patterns such as species richness.

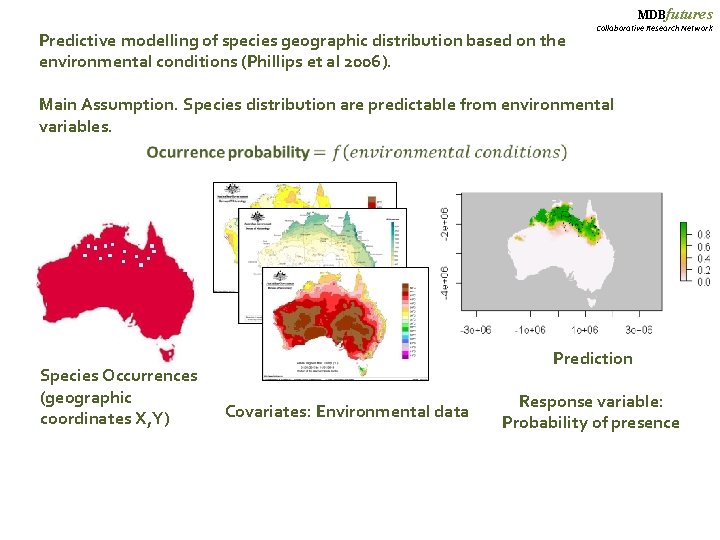
MDBfutures Predictive modelling of species geographic distribution based on the environmental conditions (Phillips et al 2006). Collaborative Research Network Main Assumption. Species distribution are predictable from environmental variables. Species Occurrences (geographic coordinates X, Y) Prediction Covariates: Environmental data Response variable: Probability of presence

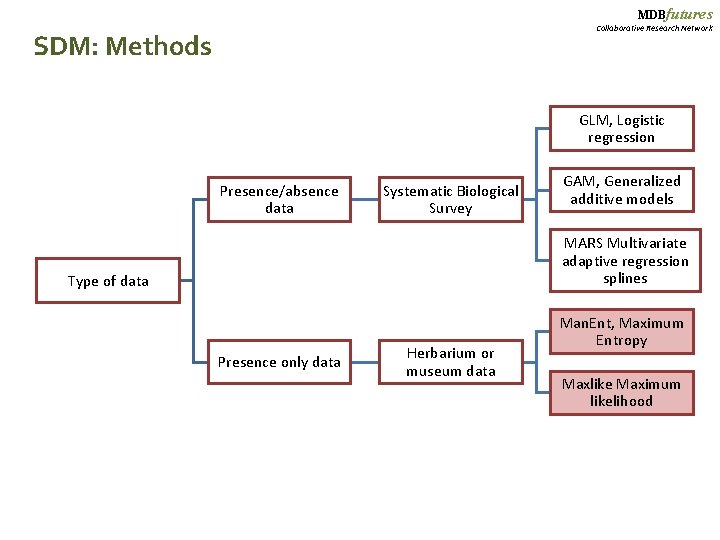
MDBfutures Collaborative Research Network SDM: Methods GLM, Logistic regression Presence/absence data Systematic Biological Survey GAM, Generalized additive models MARS Multivariate adaptive regression splines Type of data Presence only data Herbarium or museum data Man. Ent, Maximum Entropy Maxlike Maximum likelihood

MDBfutures Collaborative Research Network MAXENT MAXLIKE Machine Learning Method Maximum likelihood Method Automatic and flexible set of arrangements (Linear, Quadratic, Product, Splines) Subject to overfitting Not as flexible, arrangements need to be specified. Not possible to apply the standard statistical inference techniques. Possible to apply the standard statistical inference techniques (e. g. hypothesis test, confidence intervals or model selection) Explores the relative suitability of one place Logit-linear model which first ensures that over another using the maximum entropy the predicted value is a real probability principle. value # run & predict (in parallel) maxlike models for k randomizations acalike. Mods <- foreach(k=1: sets, . verbose=T, . packages="maxlike") %dopar% maxlike(~annual_mean_rad + I(annual_mean_rad^2) + annual_mean_temp + I(annual_mean_temp^2) +annual_precipitation + I(annual_precipitation^2) , rstrans, aca. Train[[k]], control=list(maxit=10000), remove. Duplicates=TRUE)

MDBfutures Learning Resources: Collaborative Research Network Coursera: Programming in R by Roger D. Peng, Ph. D Johns Hopkins University Data. Camp R - bloggers

MDBfutures Collaborative Research Network R list User Group There are mailing lists for R users. For more information and to subscribe, see The R Project for Statistical Computing (Mailing Lists). The primary mailing list is called "R-help"; it offers swift and competent answers to problems with R. Newsletter Since January 2001, R has had an online newsletter, which in 2009 became the R Journal.

MDBfutures Collaborative Research Network Other learning Resources. SDM Books. A. Townsend Peterson, Jorge Soberón, Richard G. Pearson, Robert P. Anderson, Enrique Martínez-Meyer, Miguel Nakamura & Miguel B. Araújo SDM and R, available Online https: //cran. rproject. org/web/packages/d ismo/vignettes/sdm. pdf Species distribution modeling with R Robert J. Hijmans and Jane Elith March 14, 2015 Janet Franklin, San Diego State University

MDBfutures Collaborative Research Network Complexities and Recommendations - Modeling formulation, modeling fitting an modeling evaluation require specific statistical methods. Conceptual modeling formulation • Variable selection Statistical Modeling • Different methods • Model selection Evaluation • Model evaluation - It is necessary to learn a set of software (e. g. Arcgis and R) and skills; computational and theoretical. - Processing time can be very extended. - As a novel methods, Information might be limited and dispersed.

Recommendations - Learn R first. It is a valuable tool to apply over a set of problems. - As some inconvenient are very specific (e. g. code or software conditions) is always a good idea google questions and read forums. - Do not hesitate to write paper’s authors. - Include all Ph. D student in the network? . THANKS!!

1) How they use the method in their work; 2) How they learned about the method – textbooks, websites, mentors; 3) Complexities they have experienced in applying the method. Conditions: No absence data.

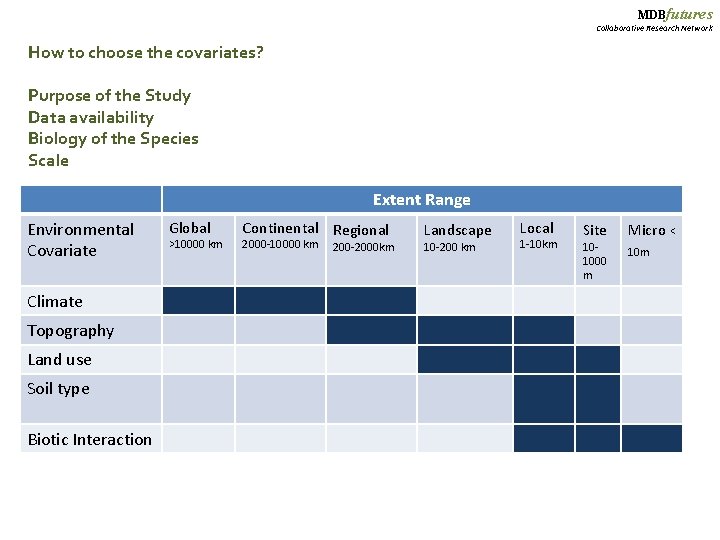
MDBfutures Collaborative Research Network How to choose the covariates? Purpose of the Study Data availability Biology of the Species Scale Extent Range Environmental Covariate Climate Topography Land use Soil type Biotic Interaction Global >10000 km Continental Regional 2000 -10000 km 200 -2000 km Landscape 10 -200 km Local 1 -10 km Site 101000 m Micro < 10 m

MDBfutures Collaborative Research Network Species Biology and SDM performance. How the biology of the species affects the model performance? (Franklin, 2009): Higher accuracy: - Rare species , better discrimination of suitability - In plants, obligate seeders - site fidelity. - Longevity.

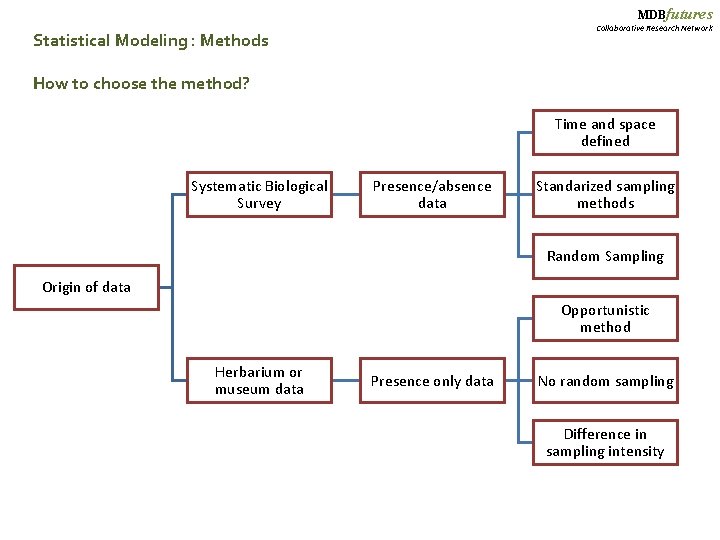
MDBfutures Collaborative Research Network Statistical Modeling : Methods How to choose the method? Time and space defined Systematic Biological Survey Presence/absence data Standarized sampling methods Random Sampling Origin of data Opportunistic method Herbarium or museum data Presence only data No random sampling Difference in sampling intensity

MDBfutures Collaborative Research Network Species Distribution Models and Presence Only data (PO). Presence–absence survey data is generally not available - Huge sampling efforts behind Museum data collection. - Urgent decisions for conservation - Only option when the landscapes extend to be modeled are significantly large. Yet, - how can we contrast the environmental conditions of Presence WITHOUT ABSENCES?

MDBfutures Max. Ent Collaborative Research Network - Follows Maximum Entropy Principle - Developed by Phillips et al. 2006. - What is Maximum Entropy Principle? What does it mean in the SDM context? Premise: the best approximation of a distribution is determined by maximum entropy, subject to constraints on it’s moments. Entropy component: Maximum Entropy model aims to find the distribution that is most spread out (i. e. closest to the uniform). Constraint component: restraint on the average of the covariates - Uses background data. locations where presence/absences are unmeasured. - Explores the relative suitability of one place over another using the maximum entropy principle F 1(z) / F(z) - F 1(z) pdf of covariates where the sp is present F(z) pdf of covariates across L

Max. Ent MDBfutures Collaborative Research Network Exponential output (raw Maxent). - Max. Ent distribution = Gibbs distribution (exponential function) - As every distributions sums to 1. - Cells with environmental variables close to the mean of presence locations have high values. Scale Dependent, not intuitite, projections no easy to interpreted Cummulative output - The value assigned to a pixel is the sum of the probabilities at that pixel and all other pixels with equal or lower probability Scale independent, easier to use in projections but is not proportional to probability of presence!! Logistic output This approximation is derived from a logistic function over the maximum entropy function Using this approximation, it is assumed that the probability of presence in a “typical site” is 0. 5!!.

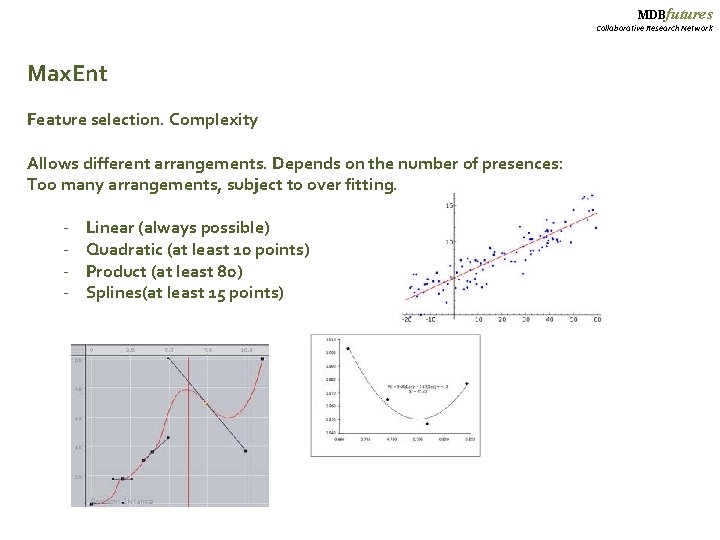
MDBfutures Collaborative Research Network Max. Ent Feature selection. Complexity Allows different arrangements. Depends on the number of presences: Too many arrangements, subject to over fitting. - Linear (always possible) Quadratic (at least 10 points) Product (at least 80) Splines(at least 15 points)

MDBfutures Collaborative Research Network Max. Ent - Most Popular Method! (Even for presence/absence data) - (over 108 (2008 -2012) used Max. Ent, 36% discarded absence. - Yackulic, 2013) - Limited customization: Number of background points Default prevalence Output format. - Variable importance.

MDBfutures Collaborative Research Network Max. Like - Statistical Method. Landscape divided by x number of pixels - Developed by Royle 2012. - Random Sampling Principle. Explore random sampling and Bayes Rule to derive the likehood for the presence-only sample. Using a hypotetical ¨first stage¨ random sample to create a ¨sample inclusion variable w(x)¨ Describe: P(x / w(x)=1, y(x)=1 ) w(x)=1 if x appears in the first stage sample y(x)=1 if the pixel is occupied - Assumptions. Species detection probability is constant.

MDBfutures Collaborative Research Network Max. Like - Possible to apply the standard statistical inference techniques (e. g. hypothesis test, confidence intervals or model selection) - Logit-linear model which first ensures that the predicted value is a real probability value - It has a R package (Maxlike) to fit the model. (Max. Ent too!!!) # run & predict (in parallel) maxlike models for k randomizations acalike. Mods <- foreach(k=1: sets, . verbose=T, . packages="maxlike") %dopar% maxlike(~annual_mean_rad + I(annual_mean_rad^2) + annual_mean_temp + I(annual_mean_temp^2) +annual_precipitation + I(annual_precipitation^2) , rstrans, aca. Train[[k]], control=list(maxit=10000), remove. Duplicates=TRUE) - Not as flexible as Max. Ent…

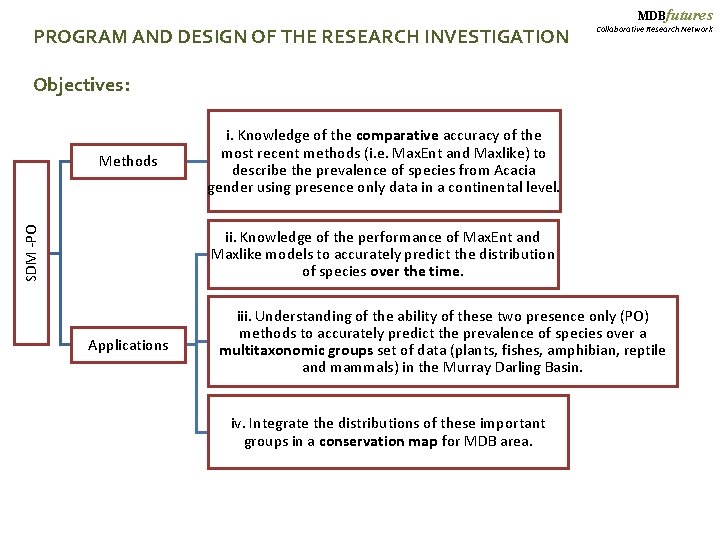
MDBfutures PROGRAM AND DESIGN OF THE RESEARCH INVESTIGATION Collaborative Research Network Objectives: SDM -PO Methods i. Knowledge of the comparative accuracy of the most recent methods (i. e. Max. Ent and Maxlike) to describe the prevalence of species from Acacia gender using presence only data in a continental level. ii. Knowledge of the performance of Max. Ent and Maxlike models to accurately predict the distribution of species over the time. Applications iii. Understanding of the ability of these two presence only (PO) methods to accurately predict the prevalence of species over a multitaxonomic groups set of data (plants, fishes, amphibian, reptile and mammals) in the Murray Darling Basin. iv. Integrate the distributions of these important groups in a conservation map for MDB area.

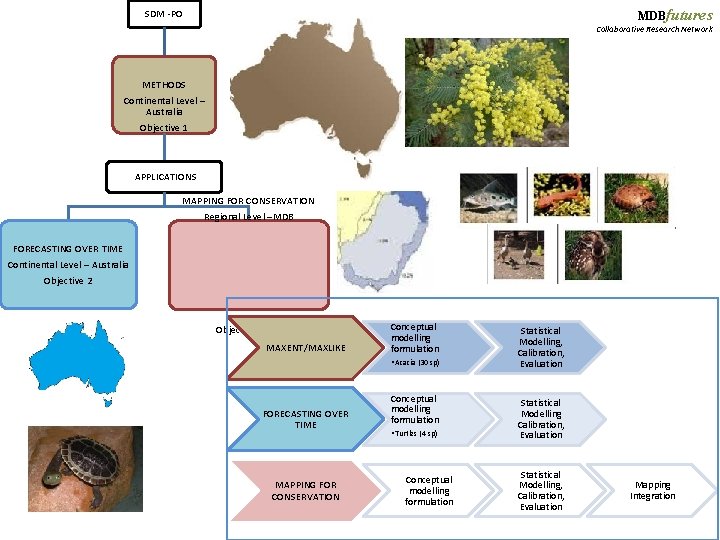
MDBfutures SDM -PO Collaborative Research Network METHODS Continental Level – Australia Objective 1 APPLICATIONS MAPPING FOR CONSERVATION Regional Level –MDB FORECASTING OVER TIME Continental Level – Australia Objective 2 Objective 3 & 4 MAXENT/MAXLIKE Conceptual modelling formulation • Acacia (30 sp) FORECASTING OVER TIME MAPPING FOR CONSERVATION Conceptual modelling formulation • Turtles (4 sp) Conceptual modelling formulation Statistical Modelling, Calibration, Evaluation Mapping Integration

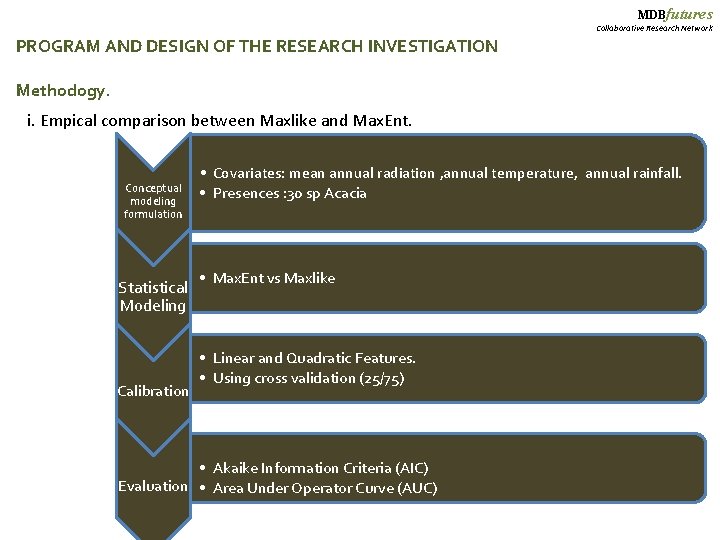
MDBfutures Collaborative Research Network PROGRAM AND DESIGN OF THE RESEARCH INVESTIGATION Methodogy. i. Empical comparison between Maxlike and Max. Ent. Conceptual modeling formulation Statistical Modeling Calibration • Covariates: mean annual radiation , annual temperature, annual rainfall. • Presences : 30 sp Acacia • Max. Ent vs Maxlike • Linear and Quadratic Features. • Using cross validation (25/75) • Akaike Information Criteria (AIC) Evaluation • Area Under Operator Curve (AUC)

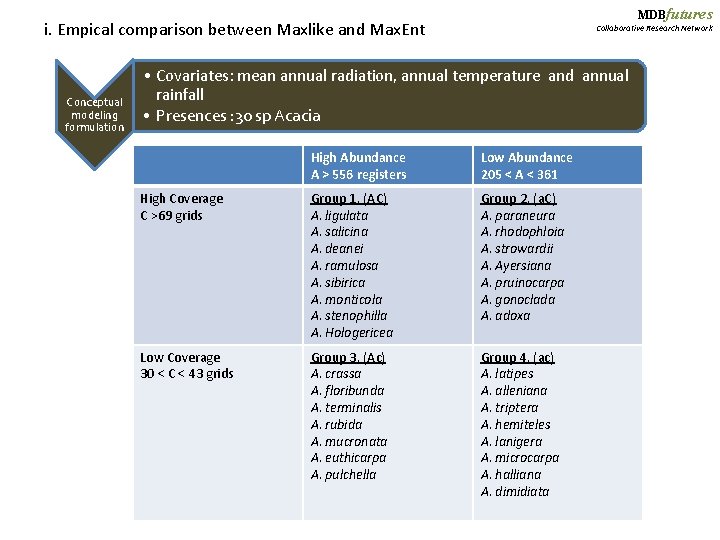
MDBfutures i. Empical comparison between Maxlike and Max. Ent Conceptual modeling formulation Collaborative Research Network • Covariates: mean annual radiation, annual temperature and annual rainfall • Presences : 30 sp Acacia High Abundance A > 556 registers Low Abundance 205 < A < 361 High Coverage C >69 grids Group 1. (AC) A. ligulata A. salicina A. deanei A. ramulosa A. sibirica A. monticola A. stenophilla A. Hologericea Group 2. (a. C) A. paraneura A. rhodophloia A. strowardii A. Ayersiana A. pruinocarpa A. gonoclada A. adoxa Low Coverage 30 < C < 43 grids Group 3. (Ac) A. crassa A. floribunda A. terminalis A. rubida A. mucronata A. euthicarpa A. pulchella Group 4. (ac) A. latipes A. alleniana A. triptera A. hemiteles A. lanigera A. microcarpa A. halliana A. dimidiata

MDBfutures Collaborative Research Network Statistical Modeling • Max. Ent vs Maxlike Response Variable Max. Ent. Suitability Index (Logistic Output) Maxlike. Probability of occurrence. Covariates Linear and Quadratic terms - mean annual radiation - annual temperature - annual rainfall

MDBfutures Collaborative Research Network • Using cross validation (25/75) • Akaike Information Criteria (AIC) Calibration • Area Under Operator Curve (AUC) & Evaluation - Cross Validation (25/75) (30 times) - AIC. Akaike Information Criteria : - < AIC, lower unexplained deviance. Better Model!! - AUC. Area Under the Receiver Operating Curve - AUC > 0. 9 - 0. 7 – 0. 9 - 0. 5 -0. 7 Very good model!! Good model! Bad model.

MDBfutures Collaborative Research Network Premilinary Results. i. Empical comparison between Maxlike and Max. Ent. Selecting 2 species per group, as follows: Group 1 (AC). A. ligulata A. sibirica Group 3 (Ac). A. A. floribunda Euthicarpa Group 2 (a. C). A. stowardii A. gonoclada Group 4 (ac). A. lanigera A. alleniana

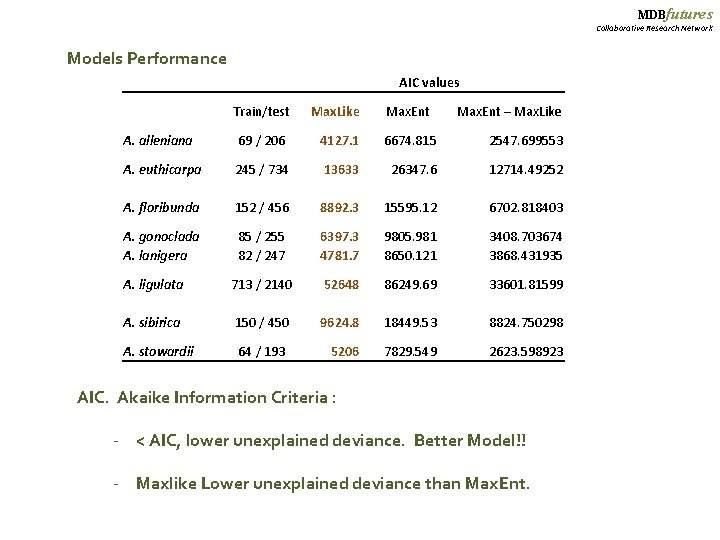
MDBfutures Collaborative Research Network Models Performance AIC values Train/test Max. Like Max. Ent – Max. Like A. alleniana 69 / 206 4127. 1 6674. 815 2547. 699553 A. euthicarpa 245 / 734 13633 26347. 6 12714. 49252 A. floribunda 152 / 456 8892. 3 15595. 12 6702. 818403 A. gonoclada A. lanigera 85 / 255 82 / 247 6397. 3 4781. 7 9805. 981 8650. 121 3408. 703674 3868. 431935 A. ligulata 713 / 2140 52648 86249. 69 33601. 81599 A. sibirica 150 / 450 9624. 8 18449. 53 8824. 750298 A. stowardii 64 / 193 5206 7829. 549 2623. 598923 AIC. Akaike Information Criteria : - < AIC, lower unexplained deviance. Better Model!! - Maxlike Lower unexplained deviance than Max. Ent.

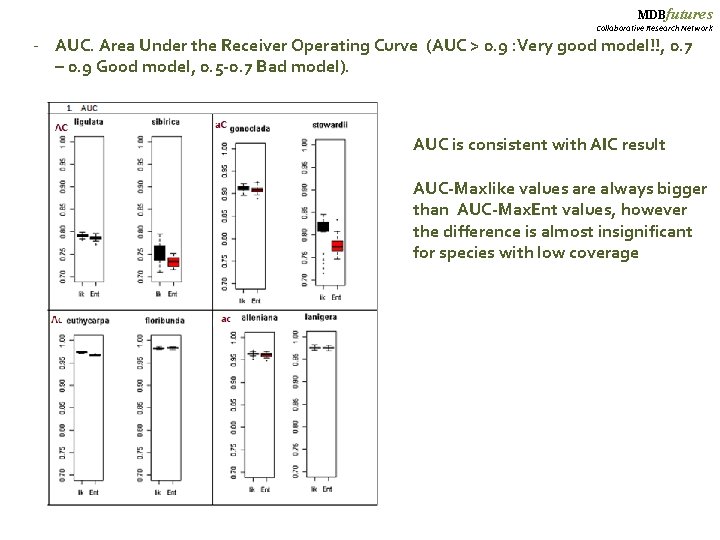
MDBfutures Collaborative Research Network - AUC. Area Under the Receiver Operating Curve (AUC > 0. 9 : Very good model!!, 0. 7 – 0. 9 Good model, 0. 5 -0. 7 Bad model). AUC is consistent with AIC result AUC-Maxlike values are always bigger than AUC-Max. Ent values, however the difference is almost insignificant for species with low coverage

MDBfutures - Mean Probability of presence. Collaborative Research Network Because of the default value of 0. 5 in Max. Ent model, mean probability of presence is close to this value. The probability of presence for Maxlike is, in most of the cases, bigger but exhibit a wide variation.

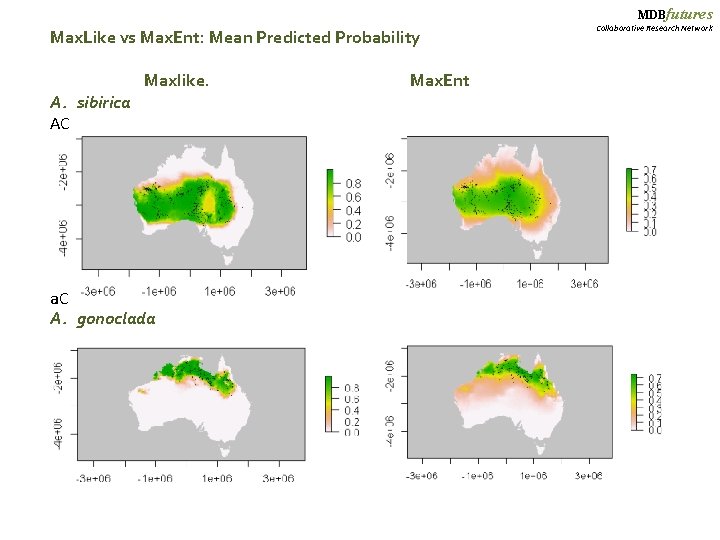
MDBfutures Max. Like vs Max. Ent: Mean Predicted Probability Maxlike. Max. Ent A. sibirica AC a. C A. gonoclada Collaborative Research Network

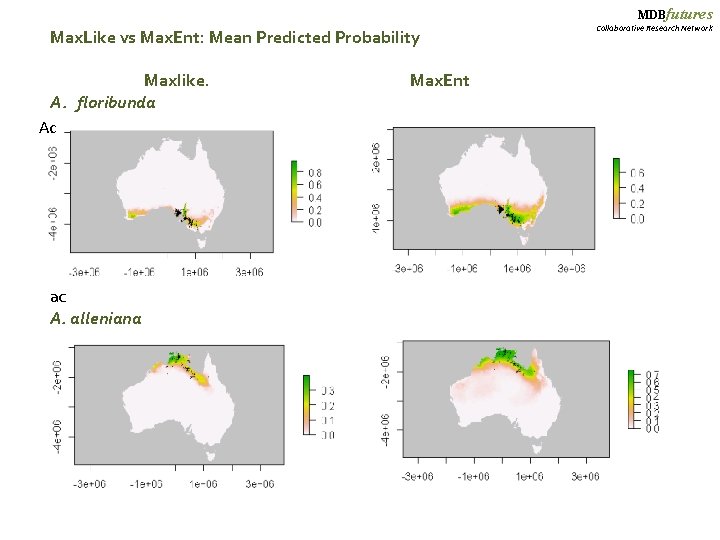
MDBfutures Max. Like vs Max. Ent: Mean Predicted Probability Maxlike. Max. Ent A. floribunda Ac ac A. alleniana Collaborative Research Network

MDBfutures Which one is the best model? : Collaborative Research Network Max. Like has better AUC and AIC values, but exhibits a huge variability. Max. Ent is more consistent between models (low variability), but maintains a “probability of presence” of around 0. 5. We will choose the model that has the best fit, taking into account the research questions, the biology of the species and the influence of omission and comission error.

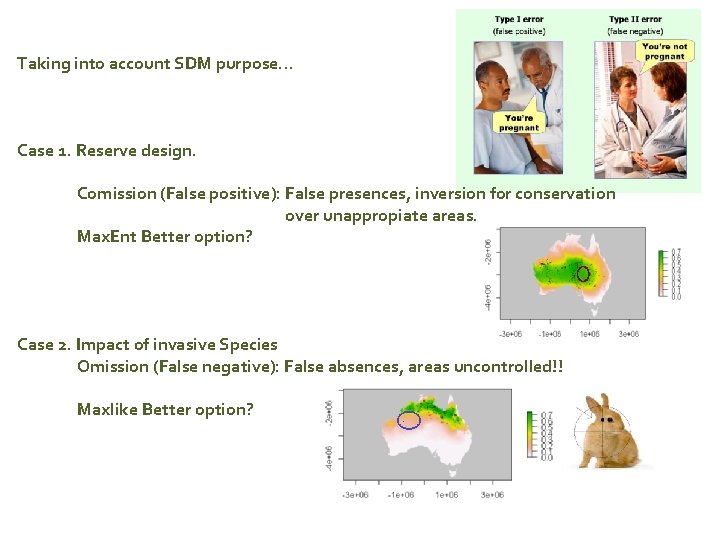
Taking into account SDM purpose… Case 1. Reserve design. Comission (False positive): False presences, inversion for conservation over unappropiate areas. Max. Ent Better option? Case 2. Impact of invasive Species Omission (False negative): False absences, areas uncontrolled!! Maxlike Better option?

ii. predict the distribution of species over the time. Conceptual modeling formulation MDBfutures Collaborative Research Network • Covariates: 19 bioclim variables, soil and water temperature? , Soil Moisture? • Presences : Turtle species Chelonia longicollis, Emydura macquarti Chelonia expansa (AUC=0. 978) Myuchelys bellii Annual mean radiation Precipitation driest quarter Lowest period moisture

MDBfutures Collaborative Research Network Resources and Funding Required Data requirement: The PO data set to be used in this project and the collaborators are: Aim 1. Acacia species, Carlos Gonzalez-Orozco Aim 2. Turtle species, Arthur Georges. Aim 3 and 4. Plants, fishes, amphibian, reptile and mammal data sets. Carlos Gonzalez-Orozco and Margarita Medina. Software requirement: R for programming. The program is free and has been obtained already. Funding source: The project is supported by Murray Darling Basin Futures project.

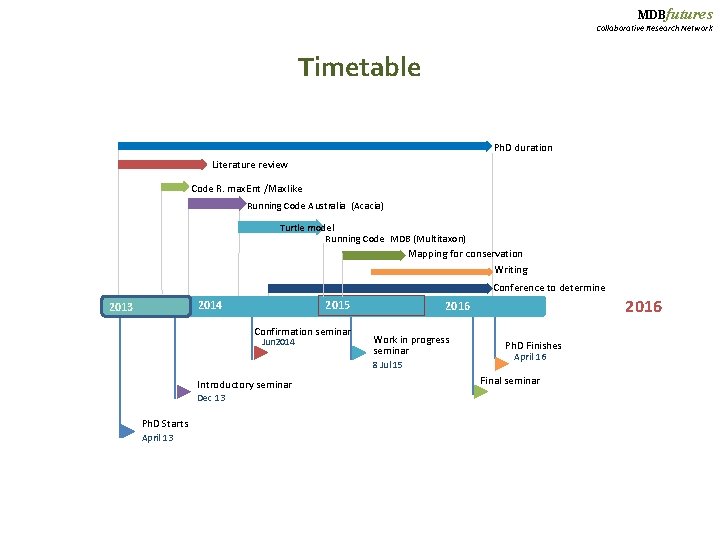
MDBfutures Collaborative Research Network Timetable Ph. D duration Literature review Code R. max. Ent /Maxlike Running Code Australia (Acacia) Turtle model Running Code MDB (Multitaxon) Mapping for conservation Writing Conference to determine 2014 2013 2015 Confirmation seminar Jun 2014 Work in progress seminar 8 Jul 15 Introductory seminar Dec 13 Ph. D Starts April 13 2016 Ph. D Finishes April 16 Final seminar

MDBfutures Collaborative Research Network Acknowledgment: 1. Funding! MDB Futures Collaborative Research Network. 2. Research Group : - Bernd Gruber - Carlos Gonzalez-Orozco - Arthur Georges - Peter Unmack - Aaron Adamack - Margarita Medina

Thanks for listening!!!!

AUC. Area under the ROC curve. A statistic generated from a receiver operating characteristic plot (ROC). AUC represents an overall performance measure of model performance across all thresholds and strengths of a prediction. AUC is a non-parametric measure that range between 0 and 1. Summarize the model’s ability to rank presence records higher than absence records (or background records in PO methods)

AIC. Akaike Information Criterion. It is a measure of the relative goodness of fit of a statistical model. It offers a relative measure of the information lost when a given model is used to describe reality. It can be said to describe the tradeoff between bias and variance in model construction, or loosely speaking between accuracy and complexity of the model. In the general case, the AIC is: AIC = 2 K - 2 ln(L) Where k is the number of parameters in the statistical model, and L is the maximized value of the likelihood function for the estimated model. Given a set of candidate models for the data, the preferred model is the one with the minimum AIC value.

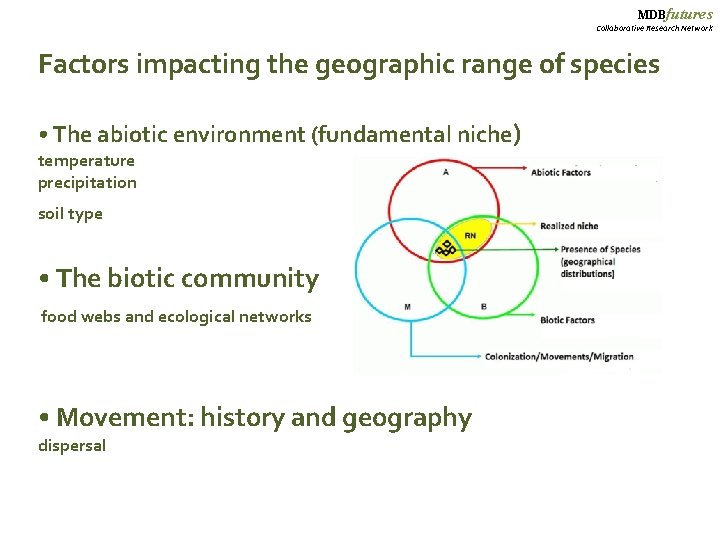
MDBfutures Collaborative Research Network Factors impacting the geographic range of species •  The abiotic environment (fundamental niche) temperature precipitation soil type •  The biotic community food webs and ecological networks •  Movement: history and geography dispersal

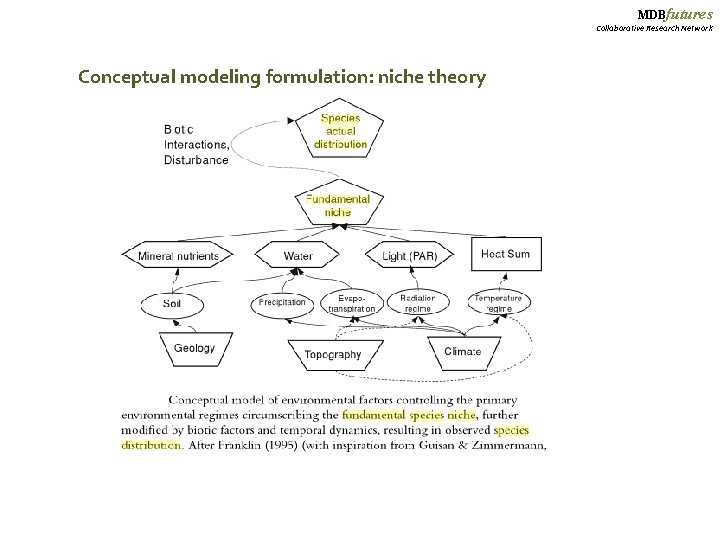
MDBfutures Collaborative Research Network Conceptual modeling formulation: niche theory

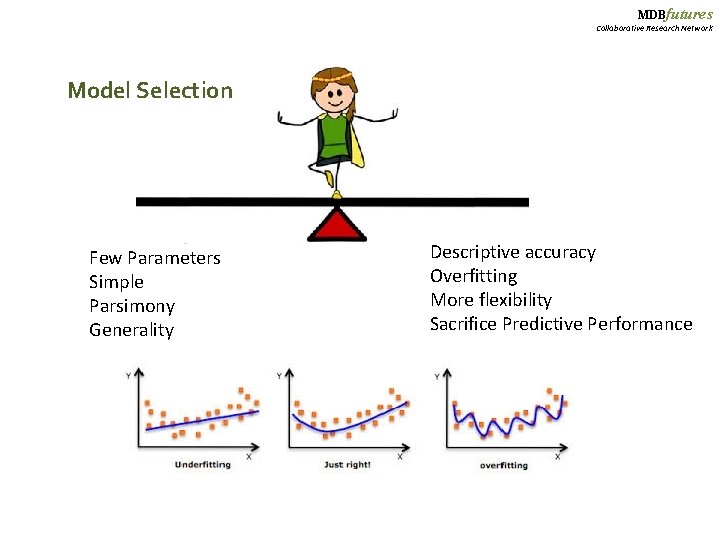
MDBfutures Collaborative Research Network Model Selection Few Parameters Simple Parsimony Generality Descriptive accuracy Overfitting More flexibility Sacrifice Predictive Performance

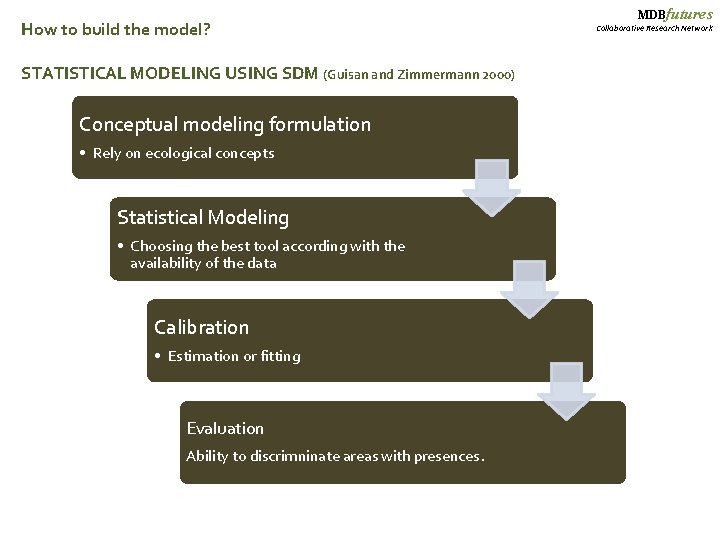
How to build the model? STATISTICAL MODELING USING SDM (Guisan and Zimmermann 2000) Conceptual modeling formulation • Rely on ecological concepts Statistical Modeling • Choosing the best tool according with the availability of the data Calibration • Estimation or fitting Evaluation Ability to discrimninate areas with presences. MDBfutures Collaborative Research Network

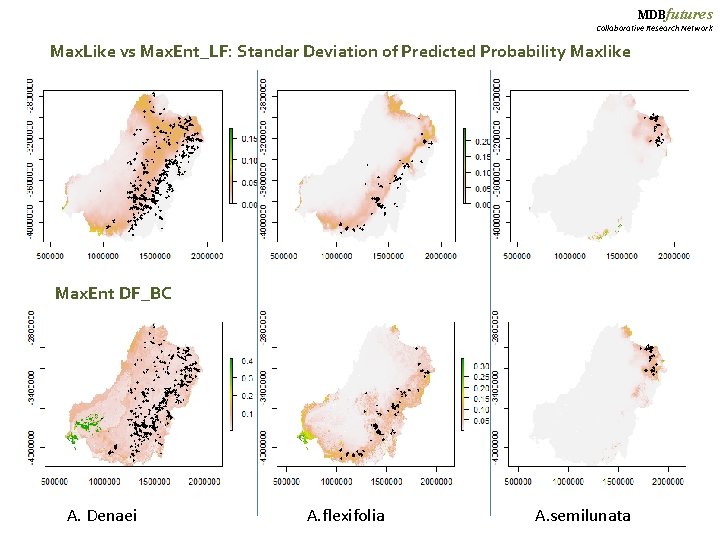
MDBfutures Collaborative Research Network Max. Like vs Max. Ent_LF: Standar Deviation of Predicted Probability Maxlike Max. Ent DF_BC A. Denaei A. flexifolia A. semilunata

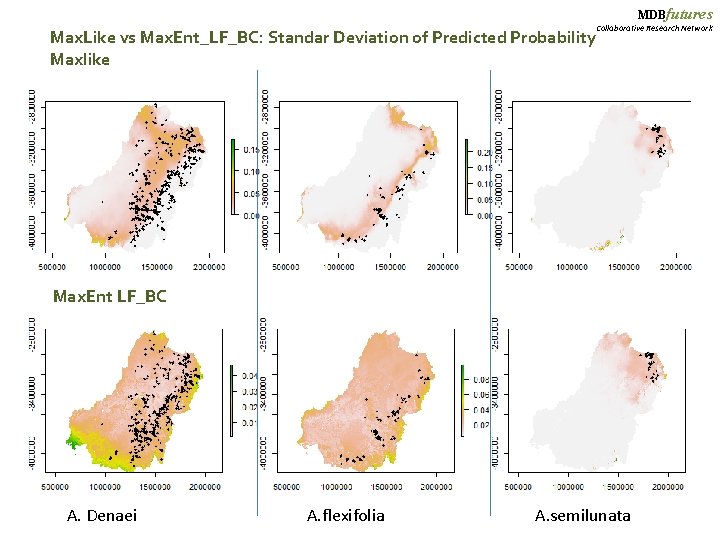
MDBfutures Collaborative Research Network Max. Like vs Max. Ent_LF_BC: Standar Deviation of Predicted Probability Maxlike Max. Ent LF_BC A. Denaei A. flexifolia A. semilunata

Objetives and Research Questions: 1. Make an empirical comparison between Max. Ent (maximun entropy) and Max. Like (maximun likelihood) in the predictions of Acacia in Australia RQ. Which of these methodologies has a better performance in the Acacia distribution? 2. Compare the performance of this methods over other species. (Eucalyptus, Fish and Frogs) in the Murray Darling Basin. RQ. Is this performance different between species and scales? 3. Integrate the distributions of this important groups in a conservation map for MDB area. RQ. Are the important areas consistent with the already defined conservation areas?

Summary Preliminary Results Maxlike Lower unexplained deviance than Max. Ent (LF, LF_BC) Max. Ent DF show better performance than Max. Ent LF A. Fexifolia (“Site fidelity sp) show a good adjustment in all the different methods. .

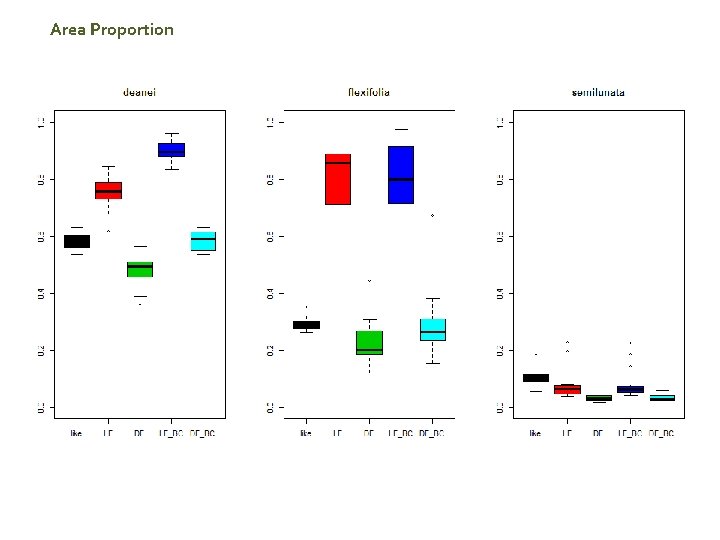
Area Proportion

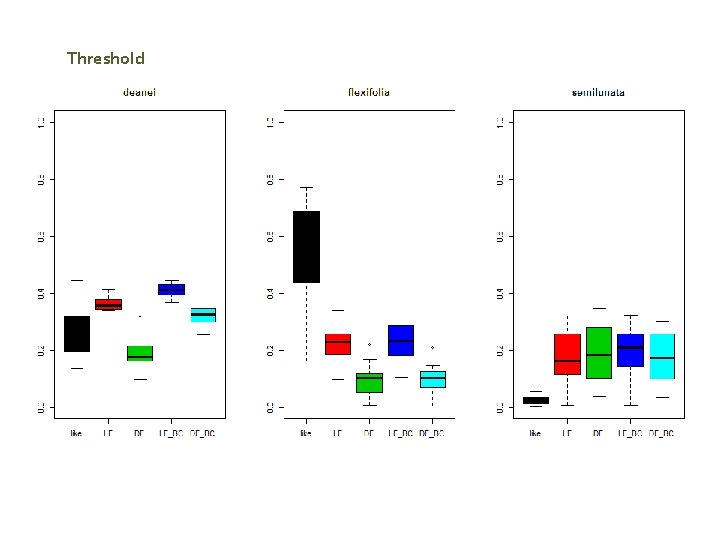
Threshold

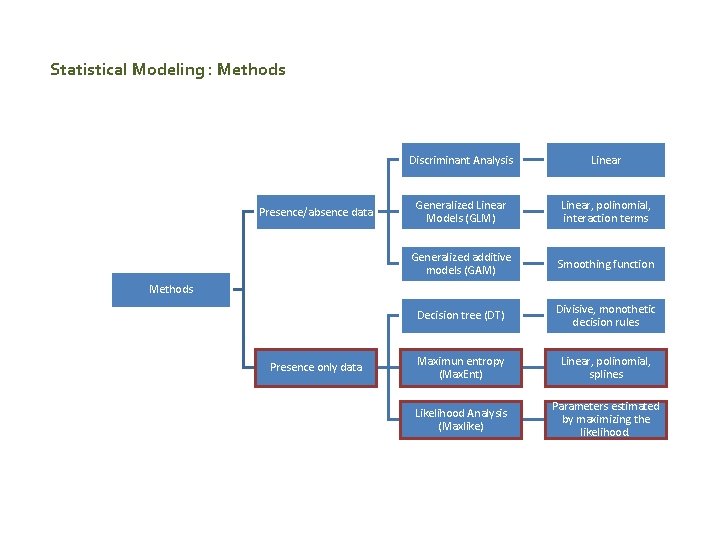
Statistical Modeling : Methods Presence/absence data Discriminant Analysis Linear Generalized Linear Models (GLM) Linear, polinomial, interaction terms Generalized additive models (GAM) Smoothing function Decision tree (DT) Divisive, monothetic decision rules Maximun entropy (Max. Ent) Linear, polinomial, splines Likelihood Analysis (Maxlike) Parameters estimated by maximizing the likelihood. Methods Presence only data

Statistical Modeling : Max. Ent Unknown

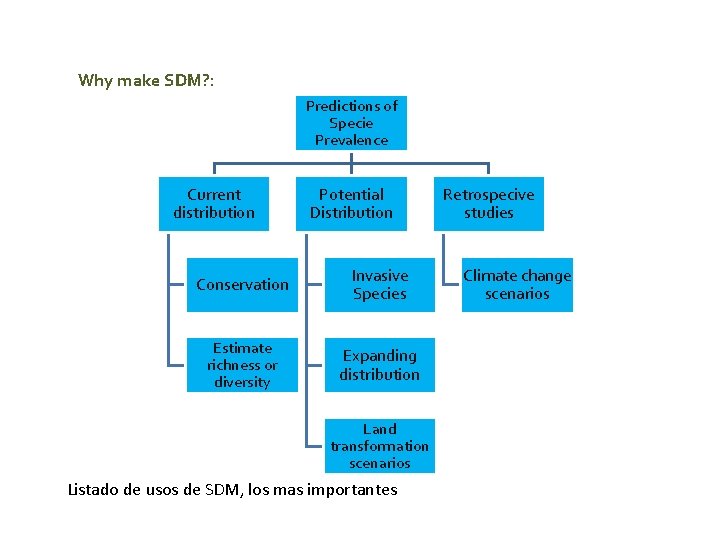
Why make SDM? : Predictions of Specie Prevalence Current distribution Potential Distribution Conservation Invasive Species Estimate richness or diversity Expanding distribution Land transformation scenarios Listado de usos de SDM, los mas importantes Retrospecive studies Climate change scenarios

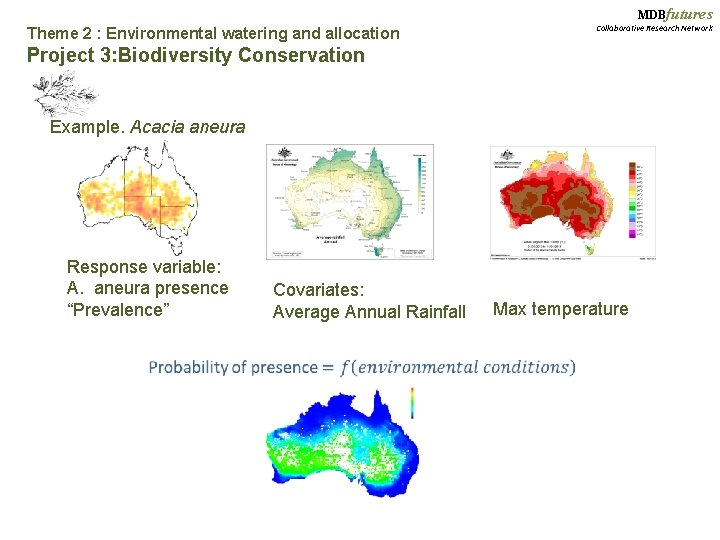
MDBfutures Theme 2 : Environmental watering and allocation Collaborative Research Network Project 3: Biodiversity Conservation Example. Acacia aneura Response variable: A. aneura presence “Prevalence” Covariates: Average Annual Rainfall Max temperature

MDBfutures Theme 2 : Environmental watering and allocation Project 3: Biodiversity Conservation Collaborative Research Network

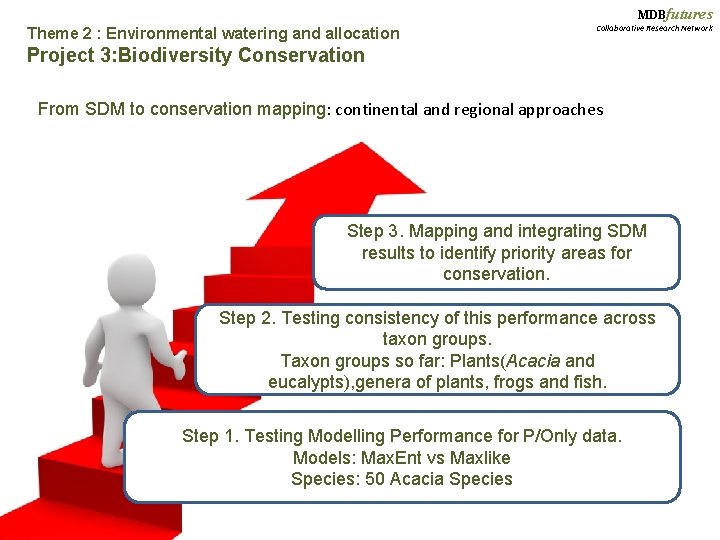
MDBfutures Theme 2 : Environmental watering and allocation Collaborative Research Network Project 3: Biodiversity Conservation From SDM to conservation mapping: continental and regional approaches Step 3. Mapping and integrating SDM results to identify priority areas for conservation. Step 2. Testing consistency of this performance across taxon groups. Taxon groups so far: Plants(Acacia and eucalypts), genera of plants, frogs and fish. Step 1. Testing Modelling Performance for P/Only data. Models: Max. Ent vs Maxlike Species: 50 Acacia Species

MDBfutures Theme 2 : Environmental watering and allocation Collaborative Research Network Project 3: Biodiversity Conservation Testing methods, Part I: Comparing Max. Ent versus Maxlike Acacia species: A. deanei (n = 809) A. flexifolia (n=203) Max. Ent: Max. Ent-Linear Features Max. Ent-All Features Max. Ent-Linear Features Bias-Corrected Max. Ent-All Features Bias-Corrected Maxlike A semilunata (n=99)

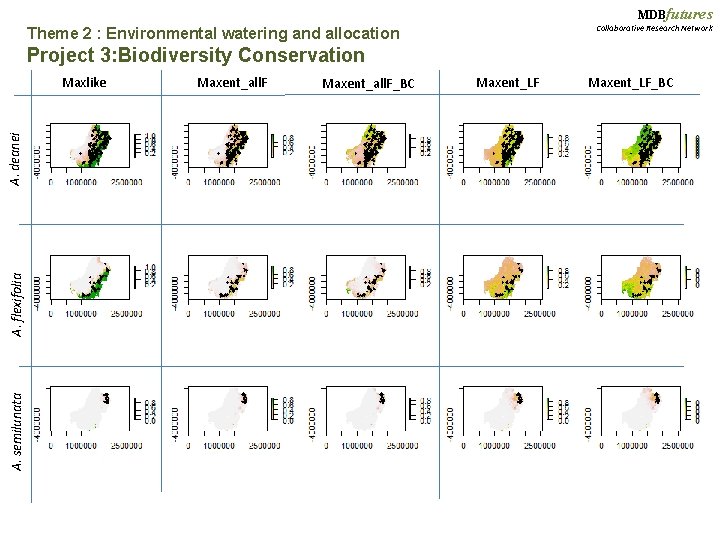
MDBfutures Collaborative Research Network Theme 2 : Environmental watering and allocation Project 3: Biodiversity Conservation A. semilunata A. flexifolia A. deanei Maxlike Maxent_all. F_BC Maxent_LF_BC

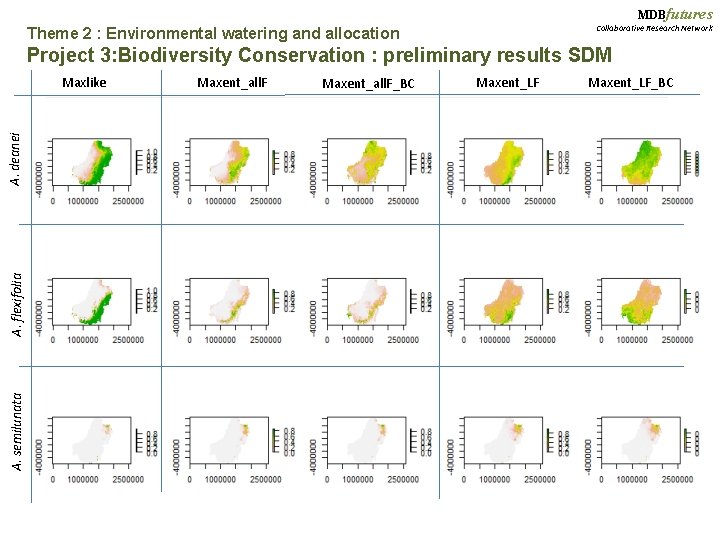
MDBfutures Collaborative Research Network Theme 2 : Environmental watering and allocation Project 3: Biodiversity Conservation : preliminary results SDM A. semilunata A. flexifolia A. deanei Maxlike Maxent_all. F_BC Maxent_LF_BC