STATISTICS Joint and Conditional Distributions Professor KeSheng Cheng

STATISTICS Joint and Conditional Distributions Professor Ke-Sheng Cheng Department of Bioenvironmental Systems Engineering National Taiwan University

Joint cumulative distribution function • Let be k random variables all defined on the same probability space ( , A, P[ ]). The joint cumulative distribution function of , denoted by , is defined as for all 2/20/2021 . Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 2

Discrete joint density 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 3

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 4

Marginal discrete density • If X and Y are bivariate joint discrete random variables, then and are called marginal discrete density functions. 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 5

Continuous Joint Density Function • The k-dimensional random variable ( is defined to be a k-dimensional continuous random variable if and only if there exists a function such that ) for all . • is defined to be the joint probability density function. 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 6

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 7

Marginal continuous probability density function If X and Y are bivariate joint continuous random variables, then and are called marginal probability density functions. 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 8

Conditional distribution functions for discrete random variables • If X and Y are bivariate joint discrete random variables with joint discrete density function , then the conditional discrete density function of Y given X=x, denoted by or , is defined to be 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 9

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 10

Conditional distribution functions for continuous random variables • If X and Y are bivariate joint continuous random variables with joint continuous density function , then the conditional probability density function of Y given X=x, denoted by or , is defined to be 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 11

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 12

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 13
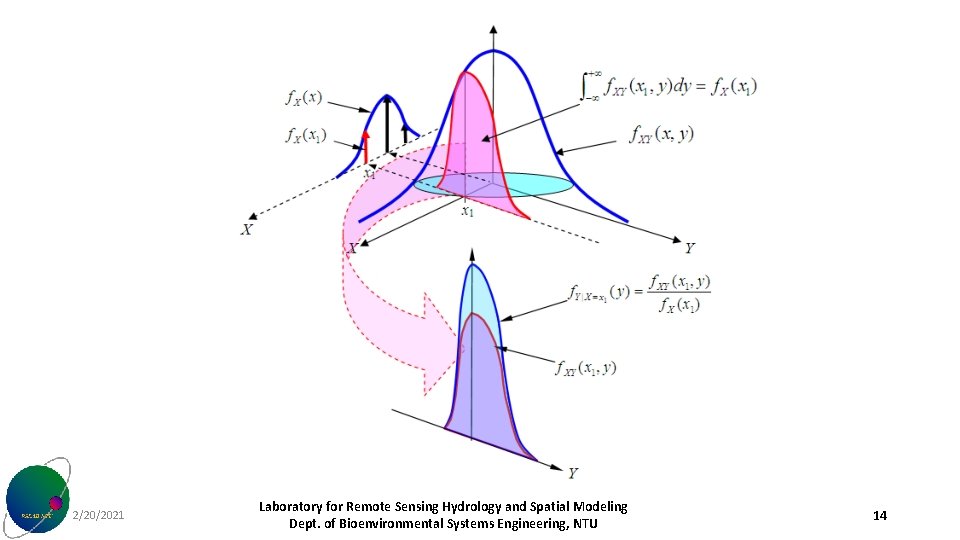
2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 14

Stochastic independence of random variables 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 15

Expectation of function of a k-dimensional discrete random variable 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 16

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 17
![Conditional Expectation E[Y|X] : Conditional expectation as a random variable. 2/20/2021 Laboratory for Remote Conditional Expectation E[Y|X] : Conditional expectation as a random variable. 2/20/2021 Laboratory for Remote](http://slidetodoc.com/presentation_image_h/03171f3179fb7e7581301d5b865cbe1f/image-18.jpg)
Conditional Expectation E[Y|X] : Conditional expectation as a random variable. 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 18

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 19

Expectation of Random Sum of Random Variables • Let N be a random variable which can assume positive integer values 1, 2, 3. . • Let X be a sequence of independent random variables which are also independent of N and have a common mean E[X] independent of i. Then the expectation of the sum of N Xi’s can be expressed as i 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 20

Covariance 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 21
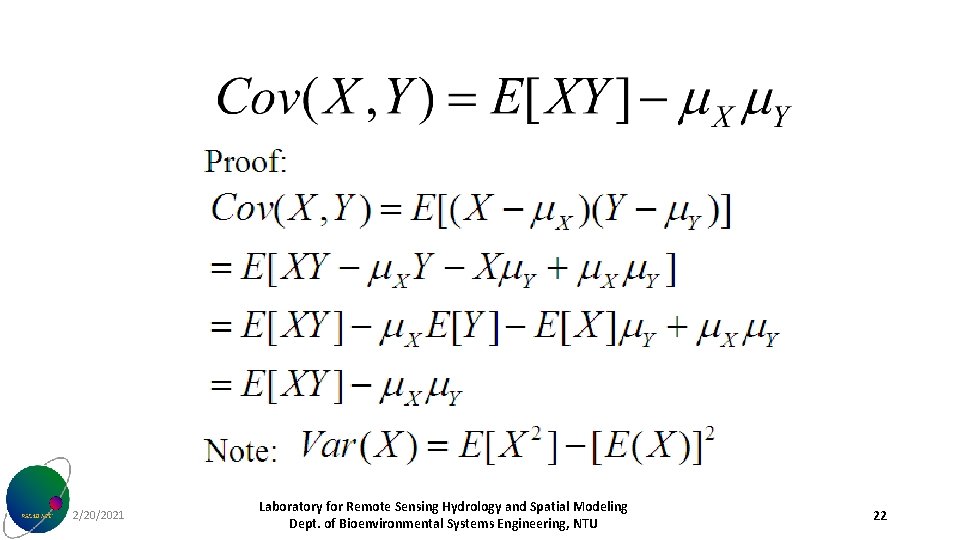
2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 22

• If two random variables X and Y are independent, then Therefore, 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 23
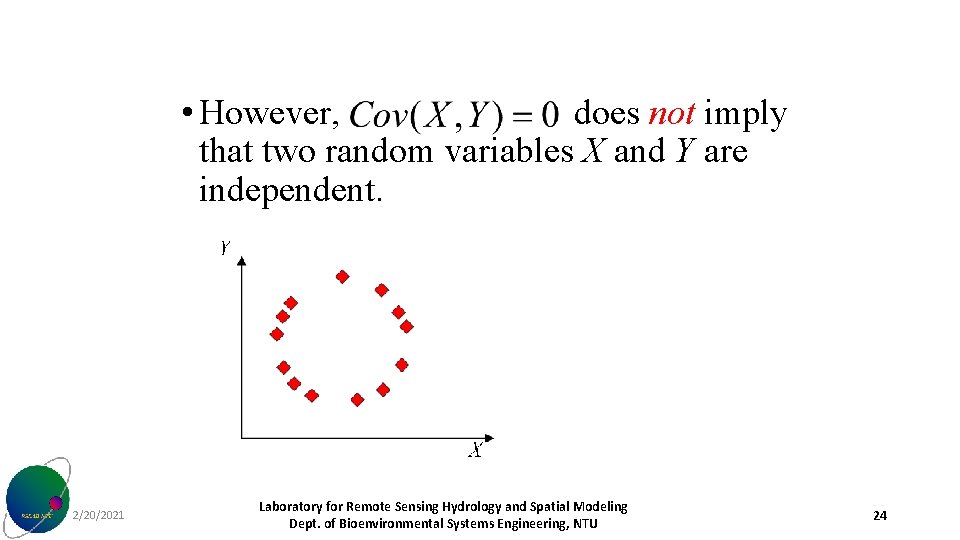
• However, does not imply that two random variables X and Y are independent. 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 24

A measure of linear correlation: Pearson coefficient of correlation 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 25
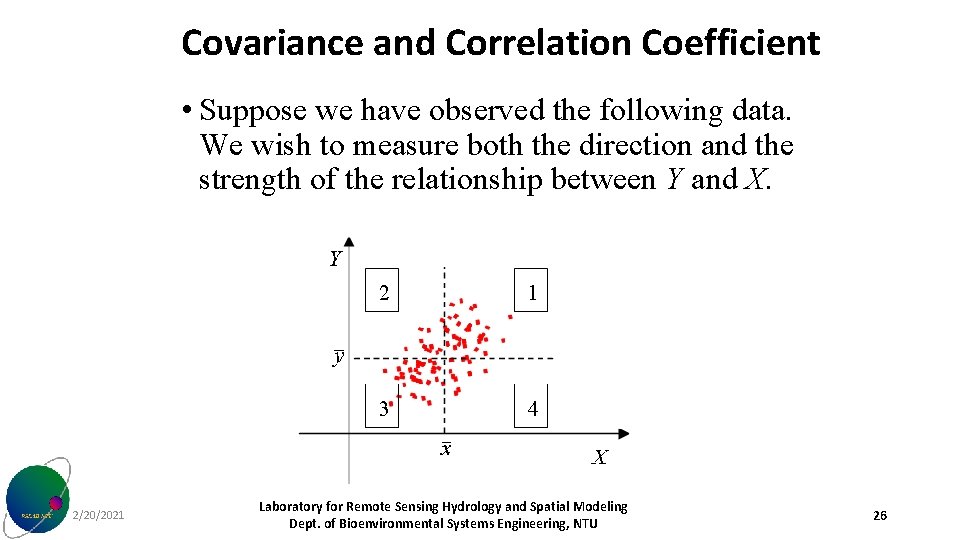
Covariance and Correlation Coefficient • Suppose we have observed the following data. We wish to measure both the direction and the strength of the relationship between Y and X. 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 26

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 27

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 28

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 29

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 30

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 31

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 32
Examples of joint distributions • Duration and total depth of storm events. (bivariate gamma, non-causal relation) • Hours spent for study and test score. (causal relation) 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 33

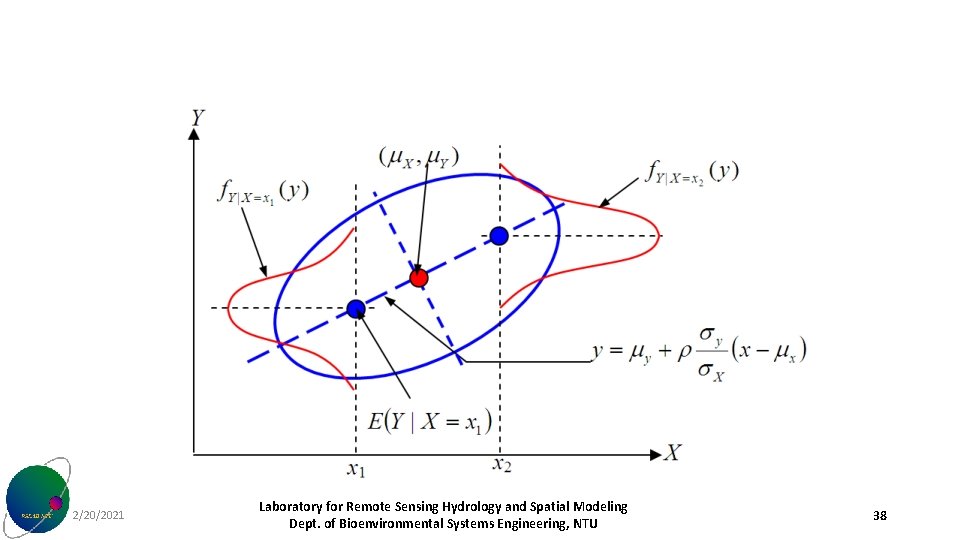
Bivariate Normal Distribution • Bivariate normal density function 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 34

• 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 35

• Conditional normal density 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 36

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 37
2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 38

Bivariate normal simulation I. Using the conditional density 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 39

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 40

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 41
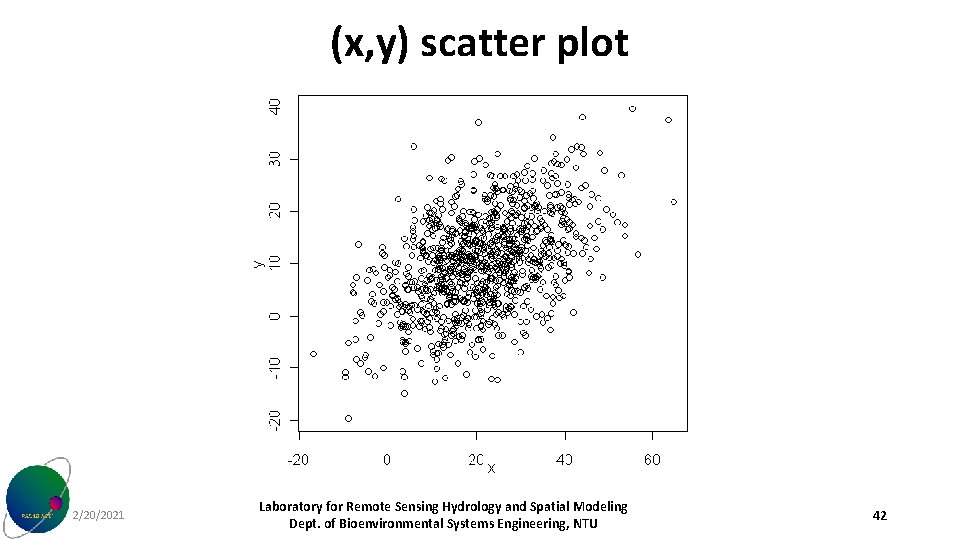
(x, y) scatter plot 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 42
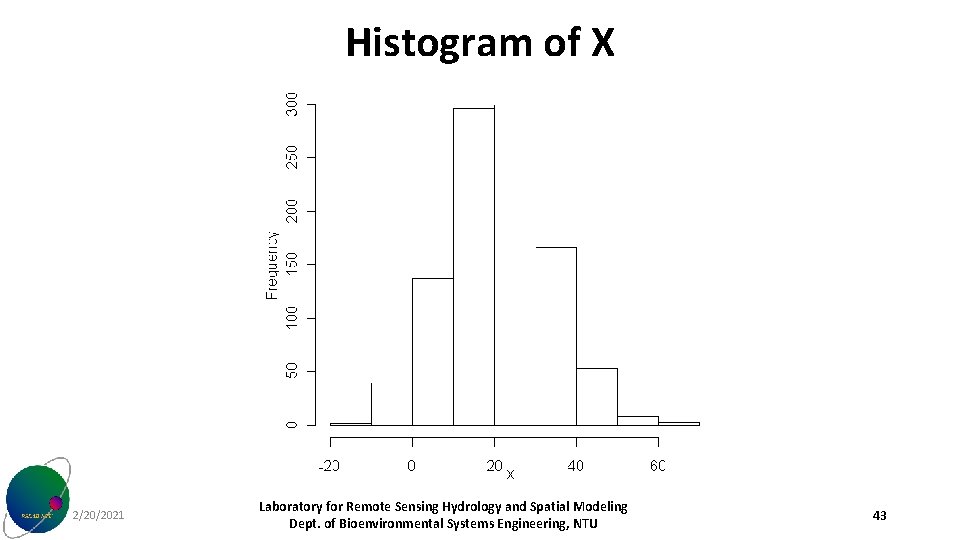
Histogram of X 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 43
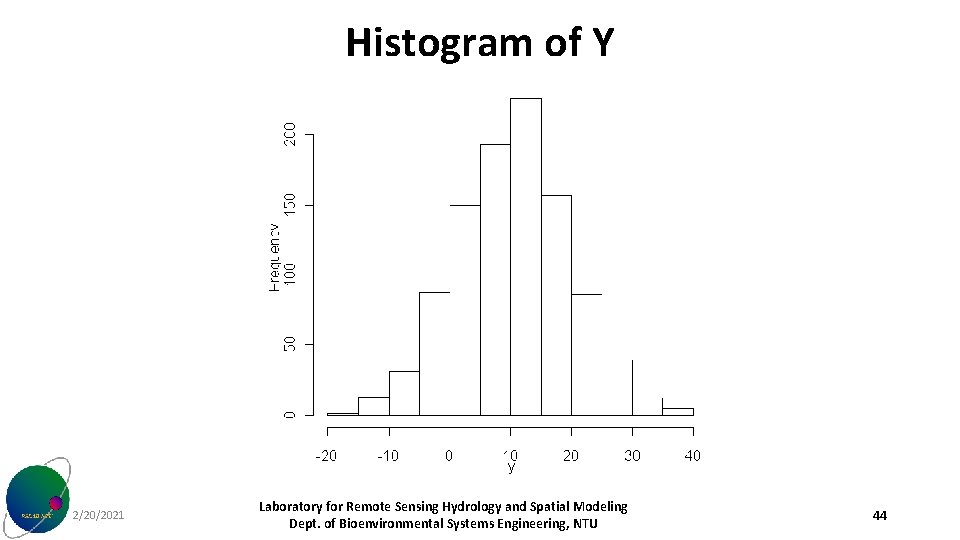
Histogram of Y 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 44
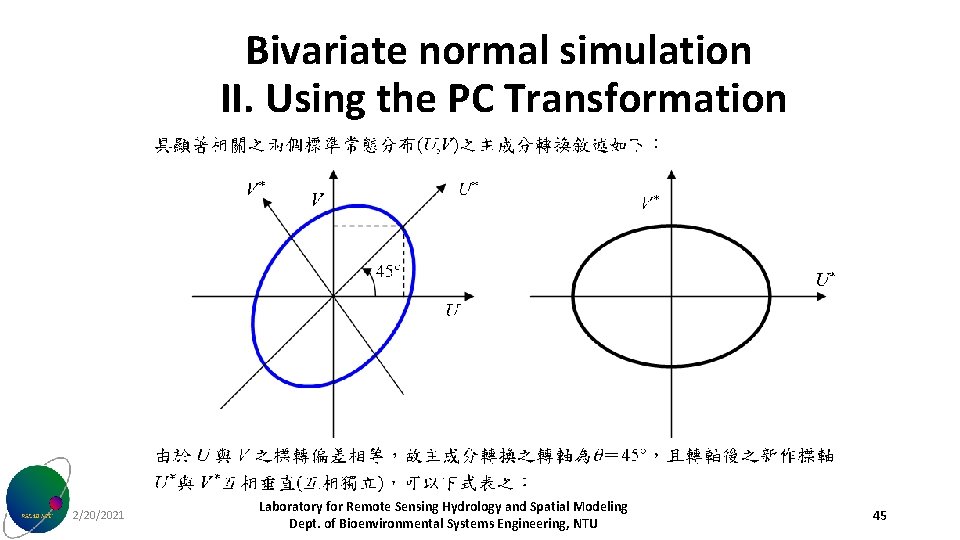
Bivariate normal simulation II. Using the PC Transformation 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 45

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 46

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 47

2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 48
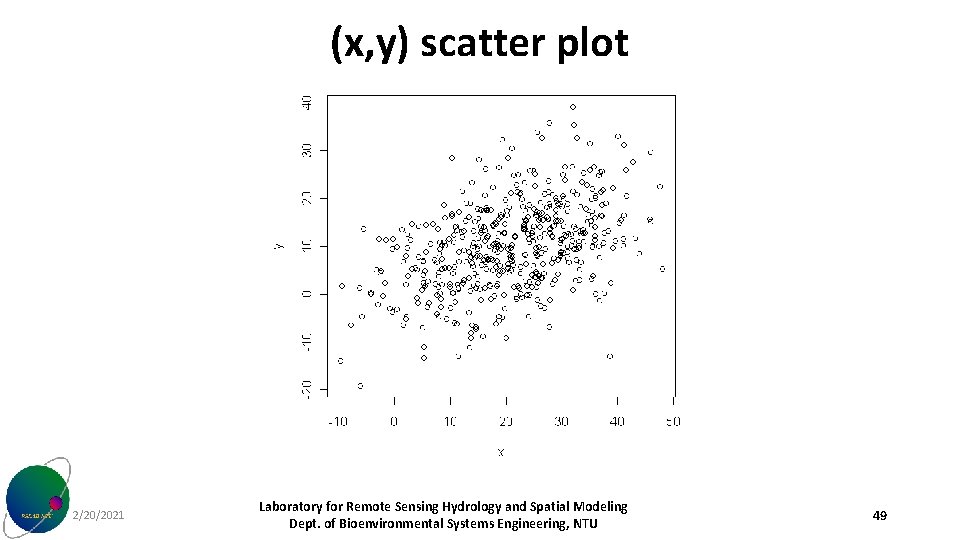
(x, y) scatter plot 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 49
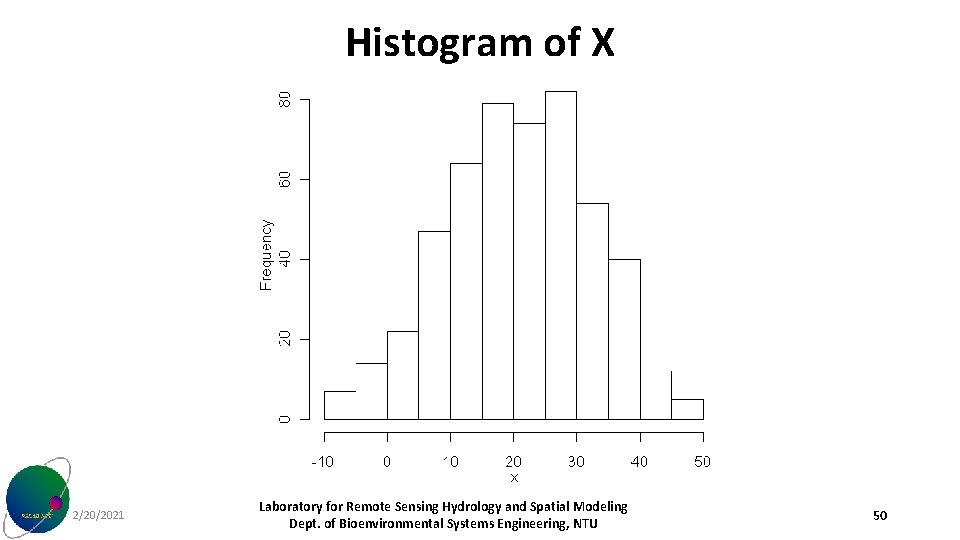
Histogram of X 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 50
Histogram of Y 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 51

Multivariate normal simulation using R • The mvtnorm package in R • dmvnorm • rmvnorm • pmvnorm • qmvnorm 2/20/2021 Laboratory for Remote Sensing Hydrology and Spatial Modeling Dept. of Bioenvironmental Systems Engineering, NTU 52
- Slides: 52