Statistics is the branch of mathematics that deals

Statistics is the branch of mathematics that deals with collecting, organizing, analyzing, and reporting quantitative information.

Data Recorded observations that can be measured or counted

Population A population is an entire set of objects sharing similar characteristics, such as human beings, automobiles, or measurements, from which data can be collected analyzed.

Sample A sample is a portion of a population from which data is collected to estimate the characteristics of the entire population.

Statistic A statistic is a measure calculated from a sample of data.

Parameter A parameter is a measure calculated from data for an entire population.

Example 1 Identify as a sample or a population: the snacks dispensed from a vending machine during its existence. population All snacks are being considered.

Example 1 Identify as a sample or a population: 100 freshman from among those enrolled at a local college for the fall of 2010. sample A small number of students is being considered.

Example 1 Identify as a sample or a population: the automobiles built by General Motors in the 1990 s. population All of the automobiles produced by the company are being considered.

Example Identify as a sample or a population: a school official gathers data about all students at Union University when studying the majors offered at the university. population

Example Identify as a sample or a population: a magazine wishes to determine the political viewpoint of college students, so it sends a questionnaire to all students at Union University. sample

Four Types of Population Sampling

1. Random—A random number generator is used to determine page number, column, and row of each person in the sample. 2. Systematic—Every thirtieth person listed in the phone book is included in the sample.

3. Convenience—A questionnaire with a return envelope is mailed out with the phone bill. 4. Cluster—Everyone whose address indicates that he lives in a particular section of town is included in the sample.

Example 2 Identify the sample as random, systematic, convenience, or cluster: math teachers who attend a workshop at the regional conference. convenience

Example 2 Identify the sample as random, systematic, convenience, or cluster: every fifth person on the class roster. systematic

Example 2 Identify the sample as random, systematic, convenience, or cluster: 500 voters, based on phone numbers chosen by computer-generated selection of page number and column in the phone book. random

Example Identify the sample as random, systematic, convenience, or cluster: A worker selects the first phone number from every page of the phone book for a phone survey. systematic

Example Identify the sample as random, systematic, convenience, or cluster: To evaluate rates for the countywide school system, the school board randomly selects two high schools and evaluates the data at those two schools. cluster

Range The range is the difference between the largest and smallest numbers in a set of data.

Mean The mean is the arithmetic average of a set of numbers (sum of data divided by the number of data).

Median The median is the middle number in a set of data arranged in numerical order. If there is an even number of data, the median is the average of the two middle numbers.

Mode The mode is the number or numbers that occur most frequently in a set of data. If no number occurs more than once, there is no mode. Data sets in which two values occur most frequently are called bimodal, while other data sets may have no mode.

Mean Average Median Middle Mode Most

Example 3 Find the range, mean, median, and mode of the following set of data: {6, 9, 7, 3, 6, 7, 10, 5}. 10, 9, 7, 7, 6, 6, 5, 3 range: 10 – 3 = 7 mean: sum of data = 53 average = 53 ÷ 8 ≈ 6. 6

Find the range, mean, median, and mode of the following set of data: {6, 9, 7, 3, 6, 7, 10, 5}. median: 10, 9, 7, 7 7, 6 6, 6, 5, 3 7 + 6 = 13 = 6. 5 2 2 mode: 6 and 7

Example 4 Find the range, mean, median, and mode of the following set of data: {58, 38, 60, 44, 45, 42, 49, 50, 41}. 38, 41, 42, 44, 45, 49, 50, 58, 60 range: 60 – 38 = 22

Find the range, mean, median, and mode of the following set of data: {58, 38, 60, 44, 45, 42, 49, 50, 41}. mean: sum of data = 427 average = 427 ÷ 9 ≈ 47. 4 median: 38, 41, 42, 44, 45 49, 50, 58, 60 mode: none

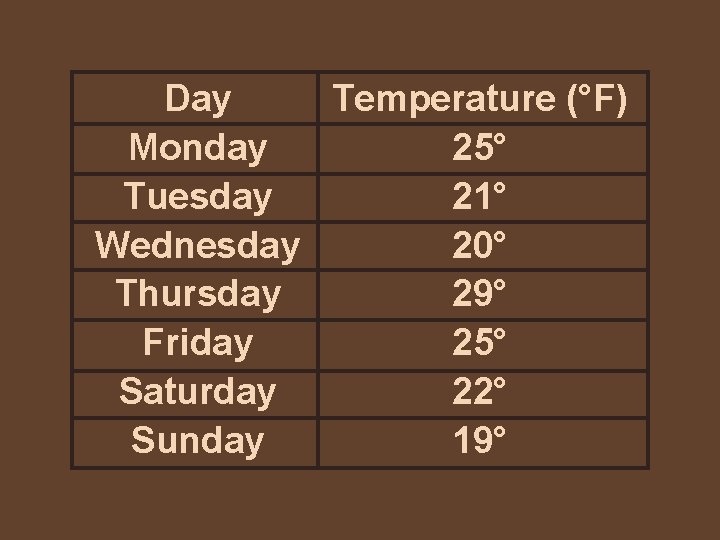
Example 5 The following are daily low temperatures from the preceding week. Find the range, mean, median, and mode of the temperatures.

Day Temperature (°F) Monday 25° Tuesday 21° Wednesday 20° Thursday 29° Friday 25° Saturday 22° Sunday 19°

29, 25, 22, 21, 20, 19 range: 29 – 19 = 10° mean: sum of data = 161 average = 161 ÷ 7 = 23° median: 29, 25, 22 22, 21, 20, 19 mode: 25°

Example Use this data to solve the following problems: A = {13, 25, 22, 18, 17, 14, 16, 22} B = {19, 22, 35, 39, 35, 37, 40, 100}

Example Arrange the data for each set in ascending order. A = {13, 14, 16, 17, 18, 22, 25} B = {19, 22, 35, 37, 39, 40, 100}

Example Find the range of each set. A = {13, 14, 16, 17, 18, 22, 25} B = {19, 22, 35, 37, 39, 40, 100} A: 12; B: 81

Example Find the median of each set. A = {13, 14, 16, 17, 18, 22, 25} B = {19, 22, 35, 37, 39, 40, 100} A: 17; B: 36

Example Find the mode of each set. A = {13, 14, 16, 17, 18, 22, 25} B = {19, 22, 35, 37, 39, 40, 100} A: 17 and 22; B: 35

Example Find the mean of each set. A = {13, 14, 16, 17, 18, 22, 25} B = {19, 22, 35, 37, 39, 40, 100} A: 18. 22; B: 40. 875

Example Would changing a single value in A always change the mean? Is this true for any set of data? A = {13, 14, 16, 17, 18, 22, 25} yes; yes

Example Would changing a single value in A always change the median? A = {13, 14, 16, 17, 18, 22, 25} no

Example If C = {12, 13, 14}, does C have three modes or no modes? no modes