Statistics in R HYPOTHESIS TESTING BY KELSEY HUNTZBERRY

Statistics in R HYPOTHESIS TESTING BY KELSEY HUNTZBERRY, MPH

Class Live Stream & Files Link To access the live stream and files for class go to my website: www. kelseyhuntzberry. com/data-science-classes/

Review of Last Week’s Material

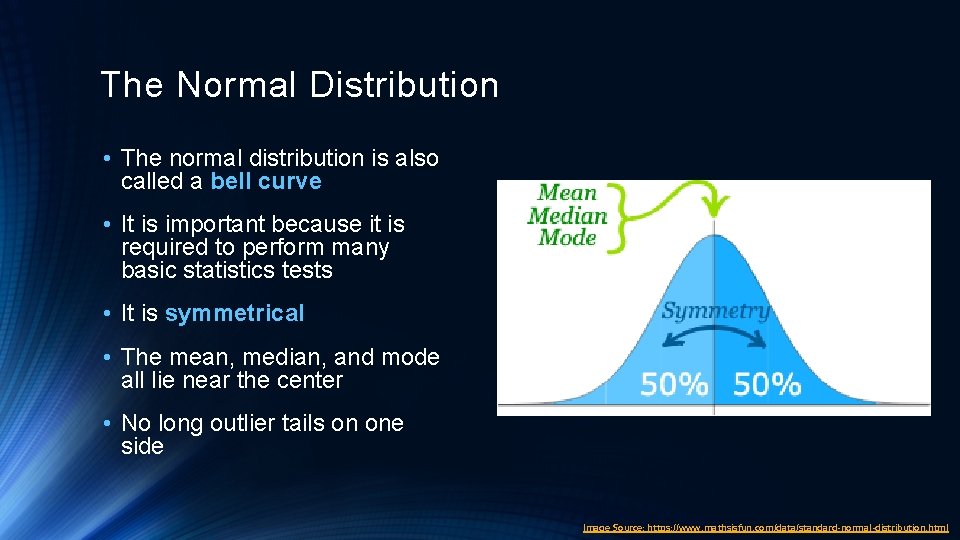
The Normal Distribution • The normal distribution is also called a bell curve • It is important because it is required to perform many basic statistics tests • It is symmetrical • The mean, median, and mode all lie near the center • No long outlier tails on one side Image Source: https: //www. mathsisfun. com/data/standard-normal-distribution. html

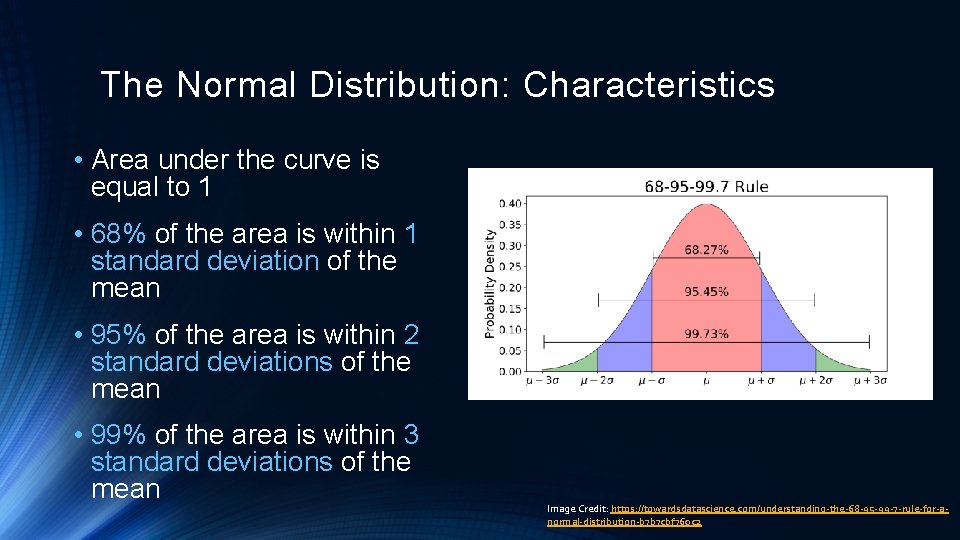
The Normal Distribution: Characteristics • Area under the curve is equal to 1 • 68% of the area is within 1 standard deviation of the mean • 95% of the area is within 2 standard deviations of the mean • 99% of the area is within 3 standard deviations of the mean Image Credit: https: //towardsdatascience. com/understanding-the-68 -95 -99 -7 -rule-for-anormal-distribution-b 7 b 7 cbf 760 c 2

Why Should You Care? • The central limit theorem allows you to make inferences from sample about a population • If your sample size is sufficiently large, it will closely resemble the entire population • You can then quantify your level of certainty you have in your conclusion • Will cover this more later when we talk about p-values

Standard Error • Standard error is calculated as follows: Or • The standard error is similar to standard deviation but accounts for sample size • The higher your sample size the smaller the standard error and vice versa • If your standard error is very high, this may indicate that your sample size is too small

Z-Scores • Z-scores are the number of standard deviations a data point is away from the mean • Used to compare a test population to a “normal” population (i. e. normally distributed) • All data points have the same units • A percentage with a z-score of 1 is equivalent to height with a z-score of 1 • Both are 1 standard deviation from the mean

Calculating Z-Scores • To calculate a z-score of a value, you take the value minus the mean of the full data divided by the standard deviation Or

What are Z-Scores Used For? • Standard errors and z-scores are used together in order to calculate a confidence intervals and p-values • We will cover confidence intervals today • We will cover p-values next week • Z-Scores are also used for outlier removal • This week I removed all outliers from a model with a zscore greater than 3 or less than -3

Confidence Intervals

Overview of Confidence Intervals • Often when we talk about statistical significance, we use a 95% confidence interval • What does this mean? • Used to measure level of certainty in calculations • A confidence interval is a range of values • If the same population is sampled many times and a confidence interval is created each time: • 95% of the intervals would contain the true population mean • Different due to random error in sampling

Overview of Confidence Intervals • Can calculate a confidence interval of a mean • Can do this for almost any statistical test or metric • The formula is: Confidence Interval = • See R code for example

How Does this Relate to Z-Scores? • We often use 85%, 90%, 95%, or 99% confidence intervals Z-Score corresponding to 95% Confidence Intervals • Choose based on the data and how certain we want to be that our conclusions are correct • For a 95% confidence interval we want to find a z-score where 95% of the area is accounted for • Visual shown on right 2. 5% of data

How Does this Relate to Z-Scores? • Why do we include area on both sides of the curve? Z-Score corresponding to 95% Confidence Intervals • We do this when we are not sure if the value we are testing is higher or lower than the mean • Called a two-sided test • Will talk about one-sided tests later today 2. 5% of data

How to Identify Critical Z-Score Value? • When 2. 5% of the data is to the right and 97. 5% is to the left, this corresponds to a z-score of 1. 96 or 1. 96 standard deviations • Can obtain by using the qnorm() function in R • Find z-scores for different alpha levels (explained more soon) on a z-score table • http: //www. z-table. com/

Complete R Code with Exercises

Null & Alternative Hypotheses

Avoiding Bias • There are widely accepted statistics procedures in place to avoid bias when performing statistical tests • Data Analysis with R lists guidelines • Assume the opposite of what you are testing • (Try to) show the results that you receive are unlikely given that assumption • Reject the assumption

Why Follow This Procedure? • Always assume there is no relationship • This helps to avoid a self-fulfilling prophecy • If you are looking for a specific answer, there will always be a way to use numbers to “prove” that point • May be subconscious or willful • Follow guidelines to remain impartial and to avoid this effect as much as possible • Do not go looking for a specific answer and tailor your method to find a specific result

Null & Alternative Hypotheses • Null Hypothesis (HO): • Assumes that any difference or significance is due to chance alone • Default hypothesis • Have to assume it is true unless proven otherwise • Have to establish statistical significance in order to reject the null hypothesis

Null & Alternative Hypotheses • Alternative Hypothesis (Ha): • Opposite of the null hypothesis HO • States that a test statistic is smaller, greater, or different than the hypothesized value in the null hypothesis • What we can conclude if we prove statistical significance and reject the null hypothesis • What you hope to prove

Null & Alternative Hypotheses • Justice system metaphor • The null hypothesis is similar to an individual on trial being innocent until proven guilty • Just because they are “presumed” guilty does not mean the are innocent • May be innocent, guilty, or there was insufficient evidence to prove guilt

Null & Alternative Hypothesis Examples What We Are Testing More than 30% of the registered voters in Travis County voted in the primary election The drug reduces cholesterol by 25% Null Hypothesis HO Alternative Hypothesis Ha Less than or equal to 30% of registered voters in Travis County voted in the primary election. The drug does not reduce cholesterol by 25% Greater than 30% of registered voters in Travis County voted in the primary election. The drug reduces cholesterol by 25% Citation: https: //courses. lumenlearning. com/introstats 1/chapter/null-and-alternative-hypotheses/

Null & Alternative Hypothesis Examples What We Are Testing Null Hypothesis HO Alternative Hypothesis Ha We want to test whether the mean GPA of students in American colleges is different from 2. 0 (out of 4. 0) The mean GPA of American colleges is 2. 0. American colleges does not equal 2. 0. We want to test if college students take less than five years to graduate from college, on the average The mean years that students take to graduate from college is greater than or equal to 5 years The mean years that students take to graduate from college is less than 5 years Citation: https: //courses. lumenlearning. com/introstats 1/chapter/null-and-alternative-hypotheses/

Try On Your Own: Hypothesis Worksheet from Github

P-Values & Statistical Significance

The Goal: Statistical Significance • Null and alternative hypotheses help you set up an experiment or analysis to answer questions systematically • The goal is to prove that something is statistically significant • This means that our results were extreme enough that they likely did not occur by chance • Quantify this using p-values

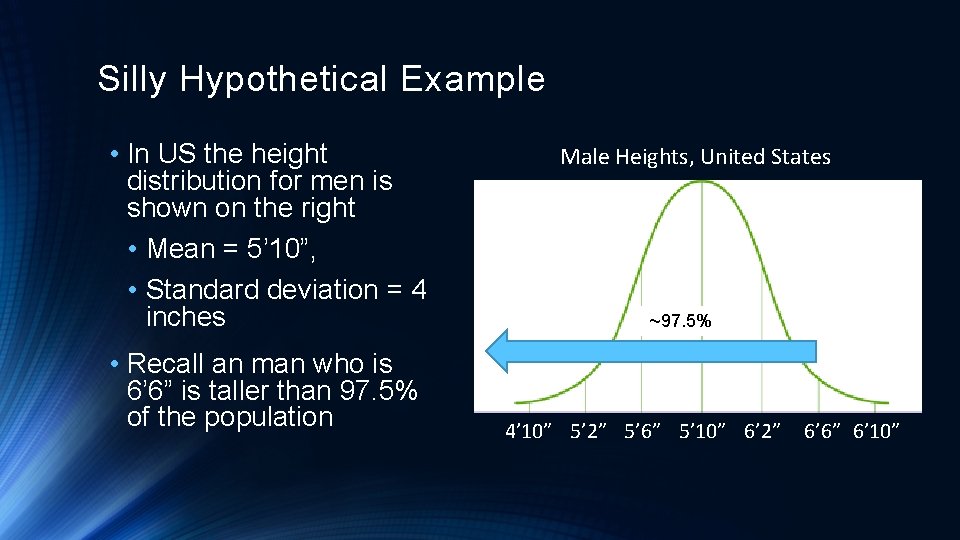
Silly Hypothetical Example • In US the height distribution for men is shown on the right • Mean = 5’ 10”, • Standard deviation = 4 inches • Recall an man who is 6’ 6” is taller than 97. 5% of the population Male Heights, United States ~97. 5% 4’ 10” 5’ 2” 5’ 6” 5’ 10” 6’ 2” 6’ 6” 6’ 10”

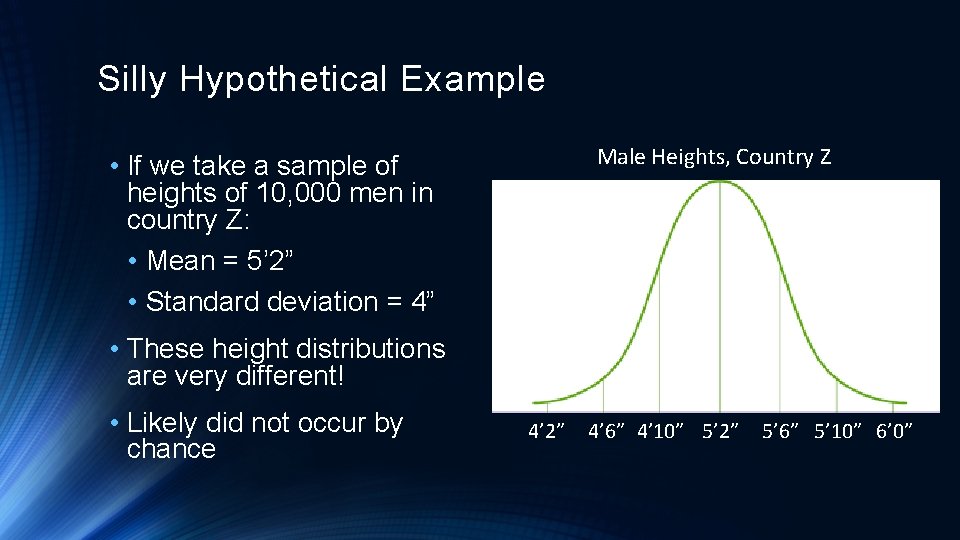
Silly Hypothetical Example Male Heights, Country Z • If we take a sample of heights of 10, 000 men in country Z: • Mean = 5’ 2” • Standard deviation = 4” • These height distributions are very different! • Likely did not occur by chance 4’ 2” 4’ 6” 4’ 10” 5’ 2” 5’ 6” 5’ 10” 6’ 0”

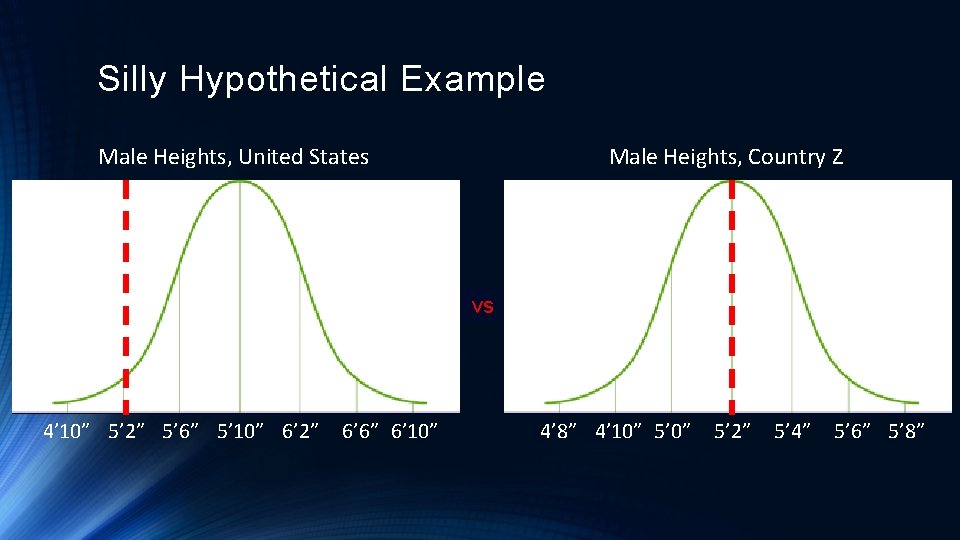
Silly Hypothetical Example Male Heights, United States Male Heights, Country Z vs 4’ 10” 5’ 2” 5’ 6” 5’ 10” 6’ 2” 6’ 6” 6’ 10” 4’ 8” 4’ 10” 5’ 2” 5’ 4” 5’ 6” 5’ 8”

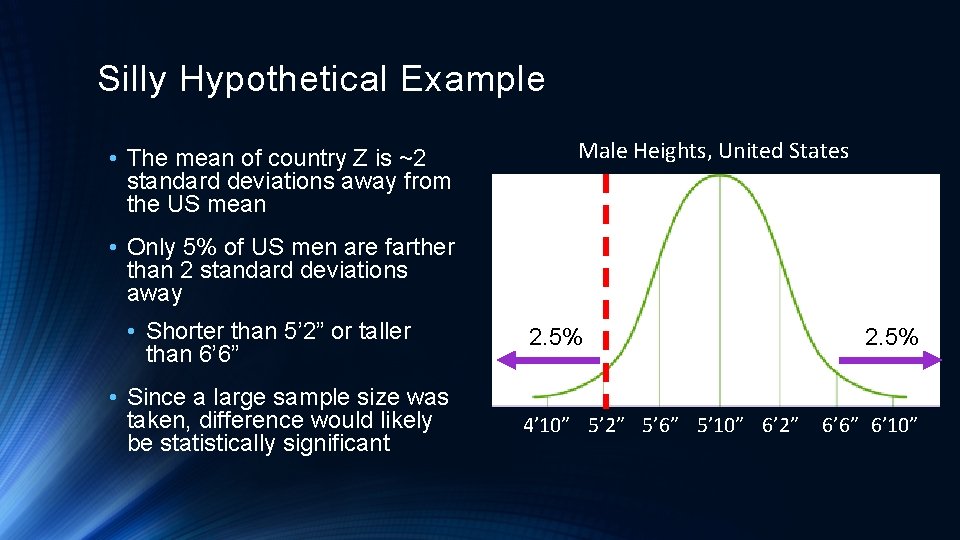
Silly Hypothetical Example • The mean of country Z is ~2 standard deviations away from the US mean Male Heights, United States • Only 5% of US men are farther than 2 standard deviations away • Shorter than 5’ 2” or taller than 6’ 6” • Since a large sample size was taken, difference would likely be statistically significant 2. 5% 4’ 10” 5’ 2” 5’ 6” 5’ 10” 6’ 2” 2. 5% 6’ 6” 6’ 10”

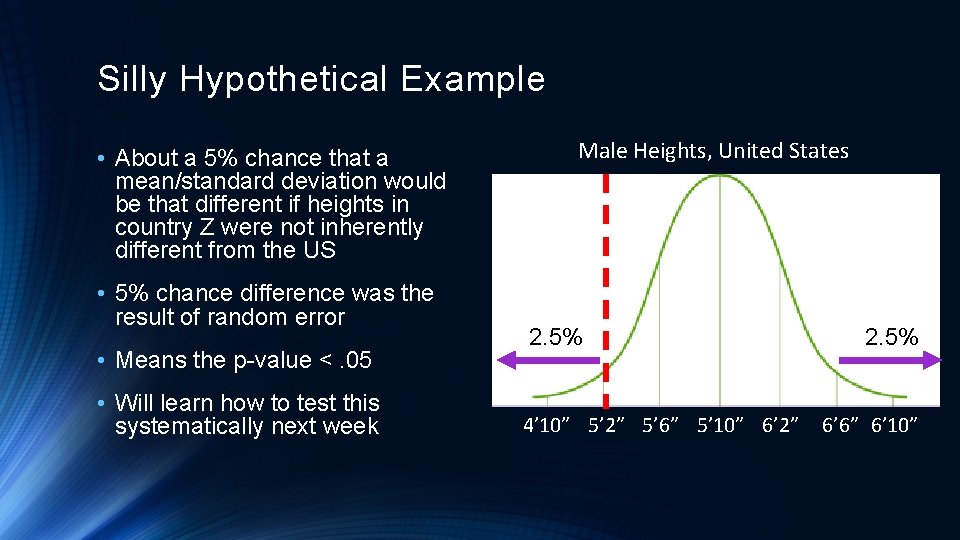
Silly Hypothetical Example • About a 5% chance that a mean/standard deviation would be that different if heights in country Z were not inherently different from the US • 5% chance difference was the result of random error • Means the p-value <. 05 • Will learn how to test this systematically next week Male Heights, United States 2. 5% 4’ 10” 5’ 2” 5’ 6” 5’ 10” 6’ 2” 2. 5% 6’ 6” 6’ 10”

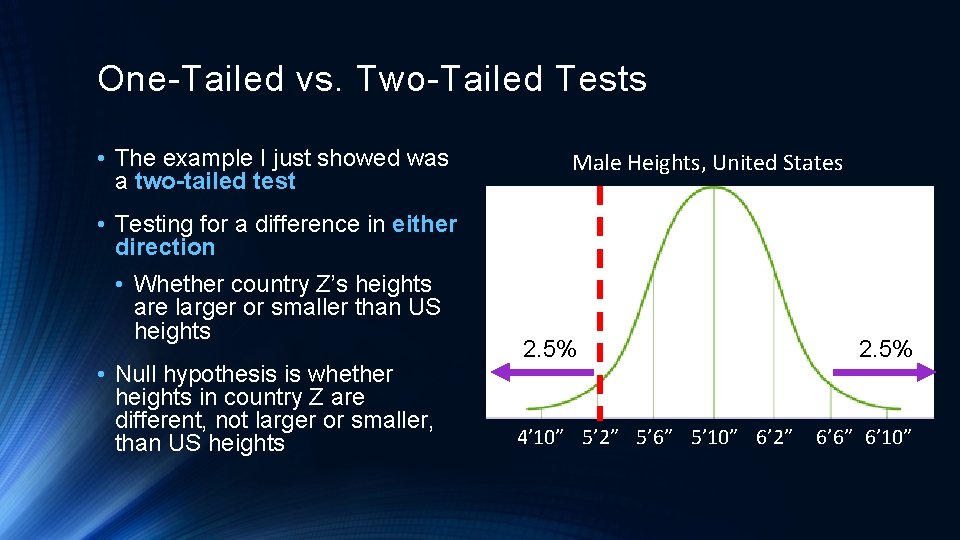
One-Tailed vs. Two-Tailed Tests • The example I just showed was a two-tailed test Male Heights, United States • Testing for a difference in either direction • Whether country Z’s heights are larger or smaller than US heights • Null hypothesis is whether heights in country Z are different, not larger or smaller, than US heights 2. 5% 4’ 10” 5’ 2” 5’ 6” 5’ 10” 6’ 2” 2. 5% 6’ 6” 6’ 10”

One-Tailed vs. Two-Tailed Tests • What if we wanted to test if country Z’s heights were significantly shorter than US heights? Male Heights, United States • This is a one-tailed test • Only tests one direction • Easier to find statistical significance with a one-tailed test • Cut off for p-value of 0. 05 is 1. 645 standard deviations away not 1. 96 5% 4’ 10” 5’ 2” 5’ 6” 5’ 10” 6’ 2” 6’ 6” 6’ 10”

Why Use a One-Tailed Test? • Only use a one-tailed test if you have a valid reason to believe your group statistic is larger or smaller than the reference group Male Heights, United States • Do not use a one-tailed test because your two-tailed p-value was greater than 0. 05 • Also, should not be used in situations of great consequence, when lives are on the line • Larger probability of random error in one-tailed statistical test 5% 4’ 10” 5’ 2” 5’ 6” 5’ 10” 6’ 2” 6’ 6” 6’ 10”

P-Value Cut Offs • General cut offs: • The standard cut off for something to be statistically significant is a p-value of 0. 05 • i. e. 1. 96 standard deviations away on either side • p < 0. 10 is generally considered marginally significant • p < 0. 01 is considered highly significant

P-Value Cut Offs • Nothing magic about 0. 05 • Your tolerance for error will depend on your use case • Bigger risk to misidentify a cancer drug as being effective than whether one soda commercial increases sales more than another • Would want a lower p-value in the case of a cancer drug

Tutorial Walk. Through A/B Testing Example from Measuring U: https: //measuringu. com/statistically-significant/

A/B Testing: What Is It? • A/B testing is used by many companies multiple websites • Example: Facebook uses this heavily • This example measures clicks • Randomly shows people one of two websites • Which website format has more clicks?

A/B Testing Example • 435 users were randomly sent to Website A or Website B • 18 out of 220 users (8%) clicked through on landing page A • 6 out of 215 users (3%) clicked through on landing page B • Is this difference statistically significant? • Use chi square to test this, will learn this in an upcoming class

A/B Testing Example • Go to https: //measuringu. com/ab-cal/ • Put in the metrics shown here from our example

A/B Testing Example • P-value = 0. 014 • The two-tailed p-value is < 0. 05 so it is statistically significant • We would expect to see a meaningless (random) difference of ~1. 4% about 14 times in 1000 • Play with the calculator • Observe how different numbers of successes changes the p-value

A/B Testing Example • Black line shows our confidence interval • Blue lines shows 5% difference for reference • Testing whether the difference in clicks (as a percent) between site A and site B is greater than 0 • Our confidence interval does not include 0 so our results are statistically significant