Statistics in R CORRELATION INTRO TO LINEAR REGRESSION

Statistics in R CORRELATION & INTRO TO LINEAR REGRESSION BY KELSEY HUNTZBERRY, MPH

Correlation

Pearson’s Correlation Coefficient Summary • Measures the strength of the linear relationship between two numeric variables • Ranges from -1 to 1 • Values closer to zero have a weaker relationship • Values closer to either -1 or 1 have stronger relationships

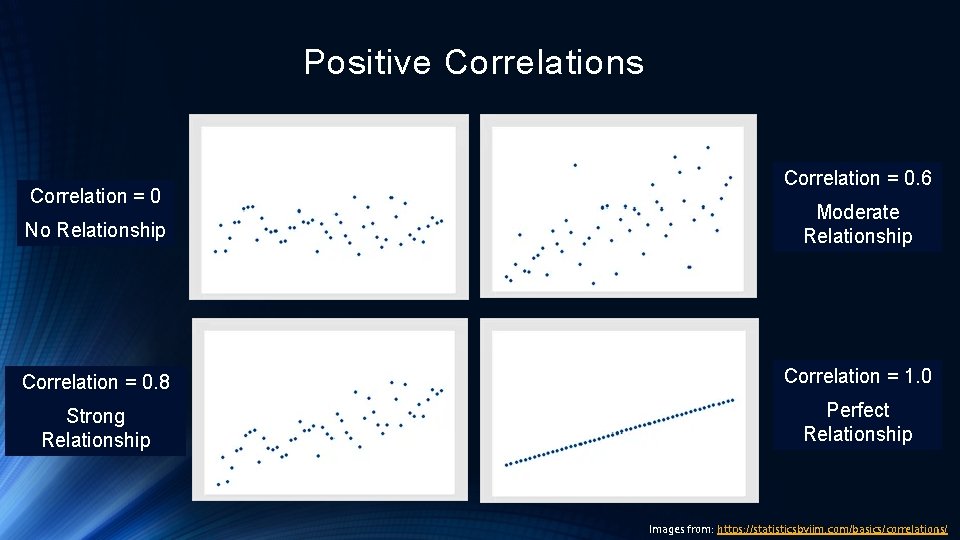
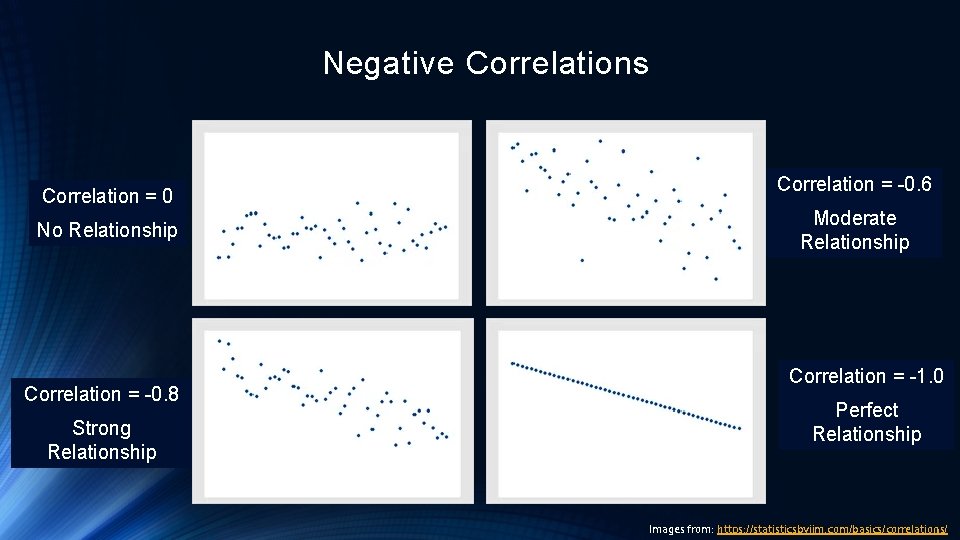
Correlation Coefficient Direction • Correlation of 0 indicates no relationship • Negative correlation coefficient indicates a negative relationship • Means one variable is rising while the other is falling • Positive correlation coefficient indicates a positive relationship • Means one variable is rising while the other is also rising

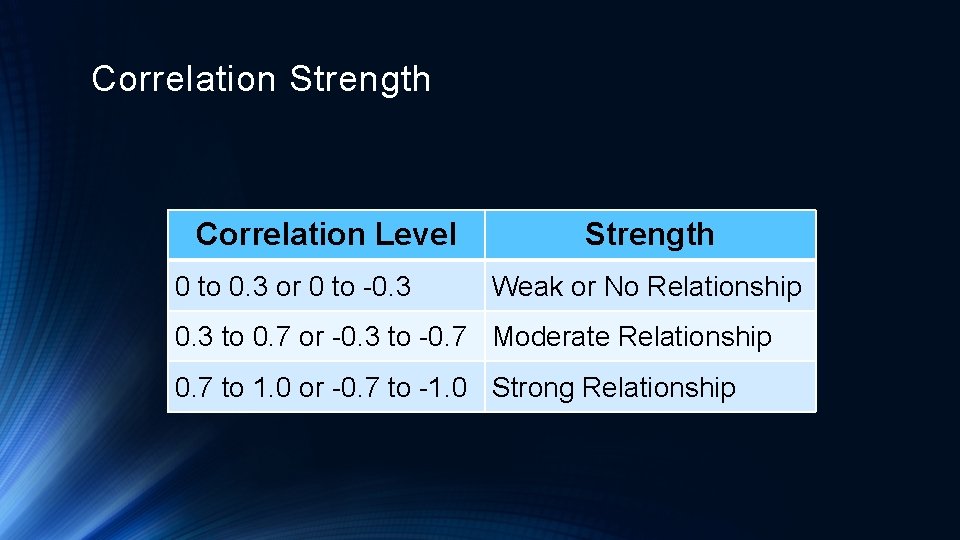
Correlation Strength Correlation Level 0 to 0. 3 or 0 to -0. 3 Strength Weak or No Relationship 0. 3 to 0. 7 or -0. 3 to -0. 7 Moderate Relationship 0. 7 to 1. 0 or -0. 7 to -1. 0 Strong Relationship

Correlation Coefficient Formula •

Positive Correlations Correlation = 0. 6 No Relationship Moderate Relationship Correlation = 0. 8 Correlation = 1. 0 Strong Relationship Perfect Relationship Images from: https: //statisticsbyjim. com/basics/correlations/

Negative Correlations Correlation = 0 No Relationship Correlation = -0. 8 Strong Relationship Correlation = -0. 6 Moderate Relationship Correlation = -1. 0 Perfect Relationship Images from: https: //statisticsbyjim. com/basics/correlations/

Assumptions for Using Correlation • Both variables must be continuous • Cannot use ordinal variables or rank correlation must be used • Pairs of observations must be independent • No major outliers • Data must be linear • Should be randomly dispersed with no pattern Images from: https: //statisticsbyjim. com/basics/correlations/

Assumptions for Significance Testing • To perform significance testing with correlation data needs to be: • Both variables must be normally distributed • Variables must have demonstrate homoskedasticity meaning they have equal variances Images from: https: //www. statisticshowto. datasciencecentral. com/homoscedasticity/

Null and Alternative Hypotheses • Test whether the correlation coefficient is significantly different from zero • Null Hypothesis: • Correlation coefficient equals zero • Alternative Hypothesis: • Correlation coefficient does not equal zero • If significant, we can assume that there is a linear association between both variables

Significance Testing • Can test to see if correlation is statistically significant • Calculate a t-statistic with the formula on the right • Use R or a t-statistic table to find p-value • Significance does not necessarily indicate a result is meaningful • Need domain knowledge

Significance Testing • Can test to see if correlation is statistically significant • Calculate a t-statistic with the formula on the right • Find degrees of freedom: n - 2 • Use R or a t-statistic table to find p-value

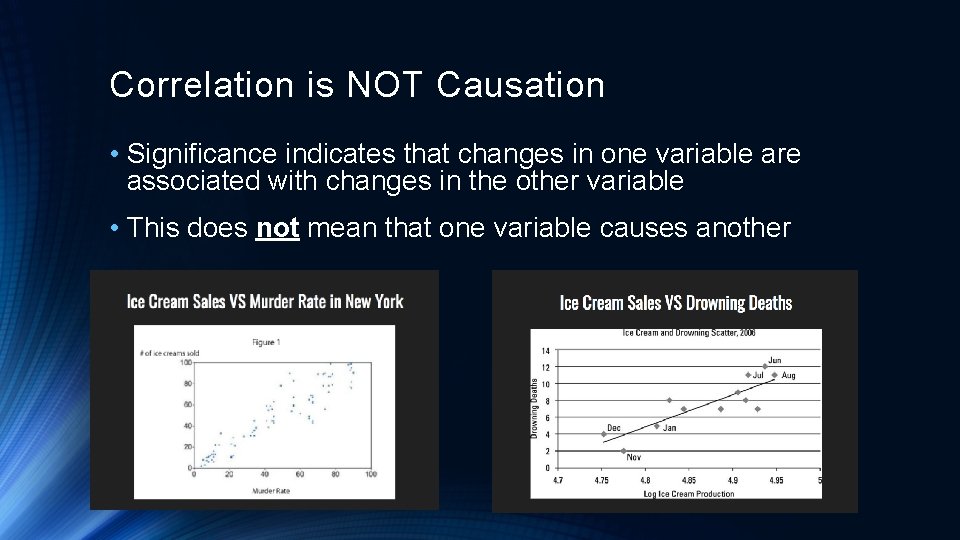
Correlation is NOT Causation • Significance indicates that changes in one variable are associated with changes in the other variable • This does not mean that one variable causes another

Correlation Coding Demo

Linear Regression

Linear Regression Summary • Linear regression is a model that predicts the relationship between one or more variables and a continuous response variable • Today we will cover simple linear regression • Models the relationship between one predictor variable and one response variable • We will cover multiple linear regression in future classes

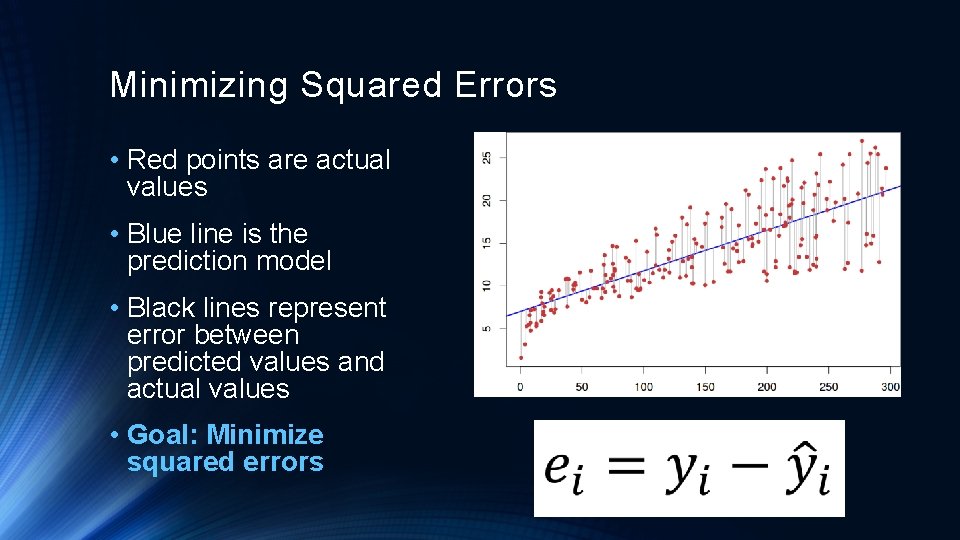
Minimizing Squared Errors • Red points are actual values • Blue line is the prediction model • Black lines represent error between predicted values and actual values • Goal: Minimize squared errors

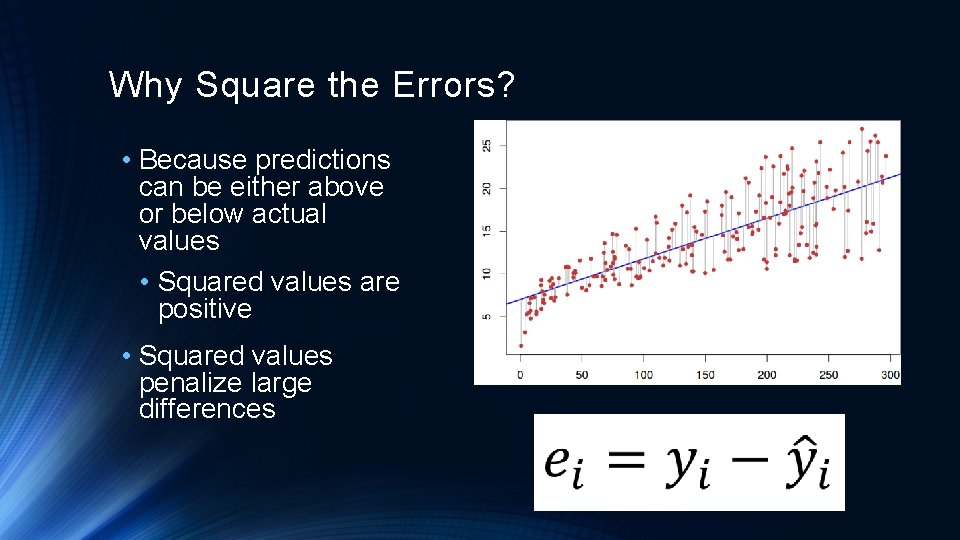
Why Square the Errors? • Because predictions can be either above or below actual values • Squared values are positive • Squared values penalize large differences

Prediction Model •

Estimate Coefficients • Use sample observations and sample means to estimate coefficients • Use slope and sample means to find y-intercept Estimate Coefficients Find Y-Intercept

What Do Coefficients Mean? •

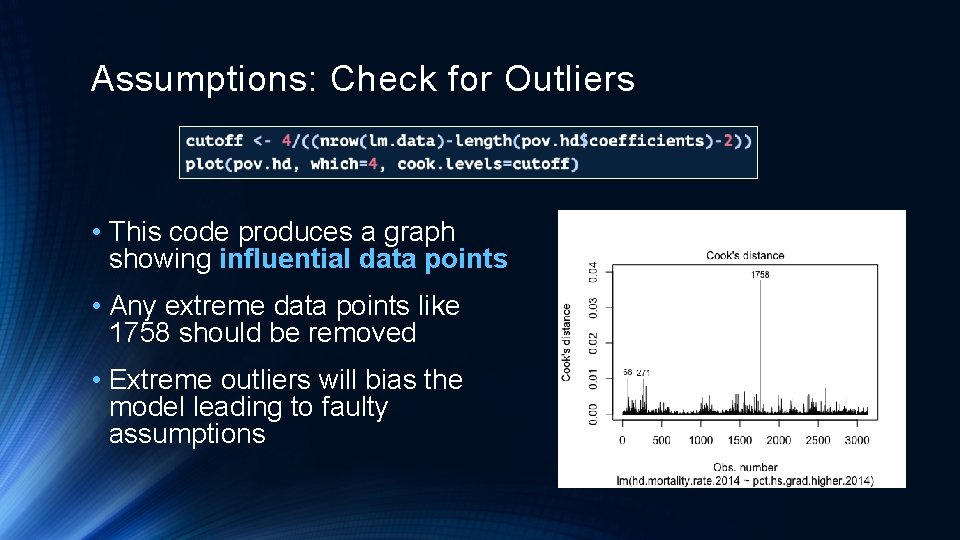
Assumptions: Check for Outliers • This code produces a graph showing influential data points • Any extreme data points like 1758 should be removed • Extreme outliers will bias the model leading to faulty assumptions

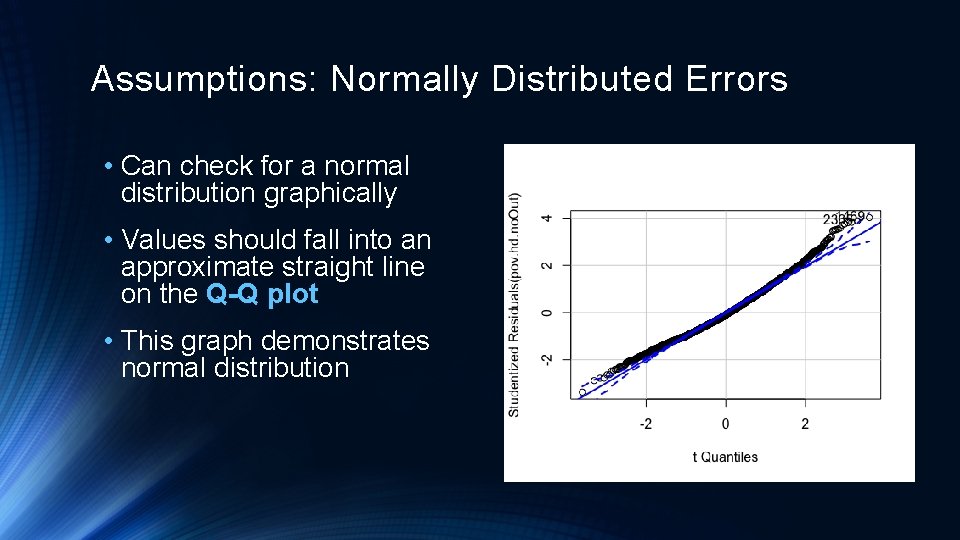
Assumptions: Normally Distributed Errors • Can check for a normal distribution graphically • Values should fall into an approximate straight line on the Q-Q plot • This graph demonstrates normal distribution

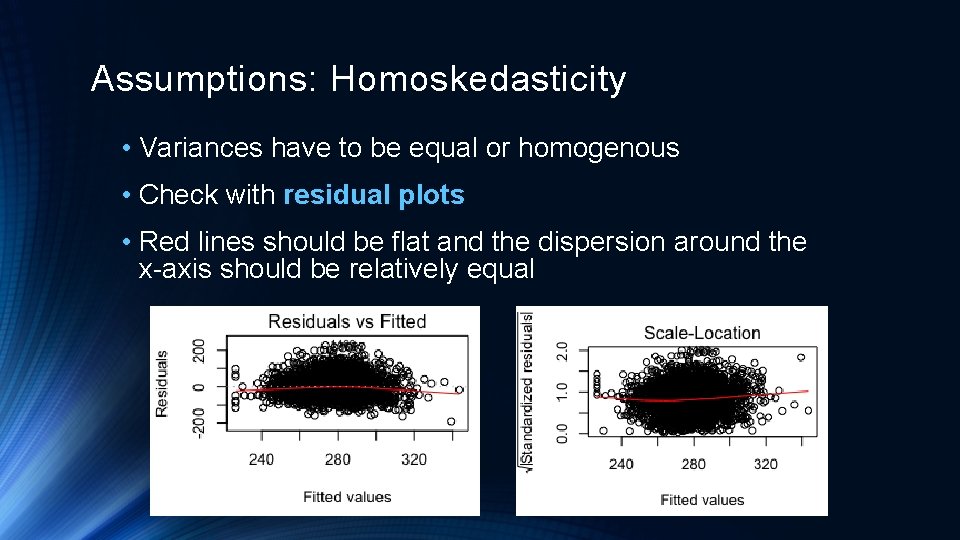
Assumptions: Homoskedasticity • Variances have to be equal or homogenous • Check with residual plots • Red lines should be flat and the dispersion around the x-axis should be relatively equal

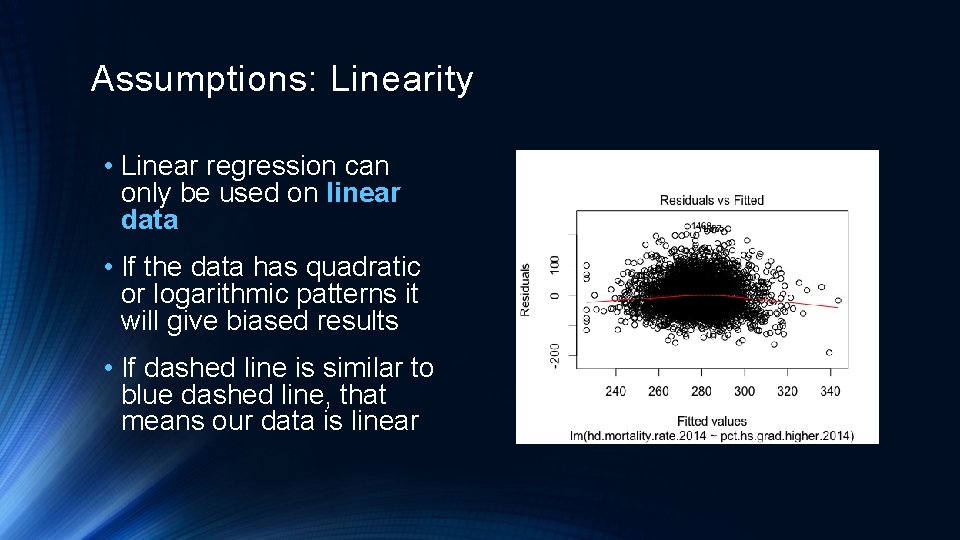
Assumptions: Linearity • Linear regression can only be used on linear data • If the data has quadratic or logarithmic patterns it will give biased results • If dashed line is similar to blue dashed line, that means our data is linear

Linear Regression Coding Demo

Next Statistics Class • Class date and time: January 11 th from 10: 30 AM – 12: 30 PM • At Milwood Library • Today we covered how to build a linear regression • On January 11 th we will discuss: • How to evaluate and tune a linear regression model • Begin with logistic regression

Useful Links for Learning Correlation and Linear Regression • https: //statisticsbyjim. com/basics/correlations/ • https: //courses. lumenlearning. com/introstats 1/chapter/testingthe-significance-of-the-correlation-coefficient/ • https: //towardsdatascience. com/linear-regressionunderstanding-theory-7 e 53 ac 2831 b 5 • http: //www. sthda. com/english/articles/40 -regression-analysis/ • http: //www. sthda. com/english/articles/39 -regression-modeldiagnostics/161 -linear-regression-assumptions-and-diagnosticsin-r-essentials/

Questions?