Statistics in Hydrology Mean median and mode central

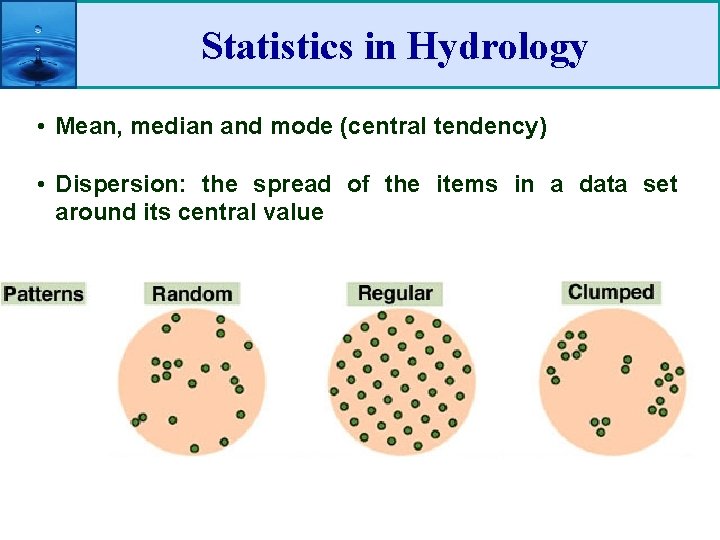
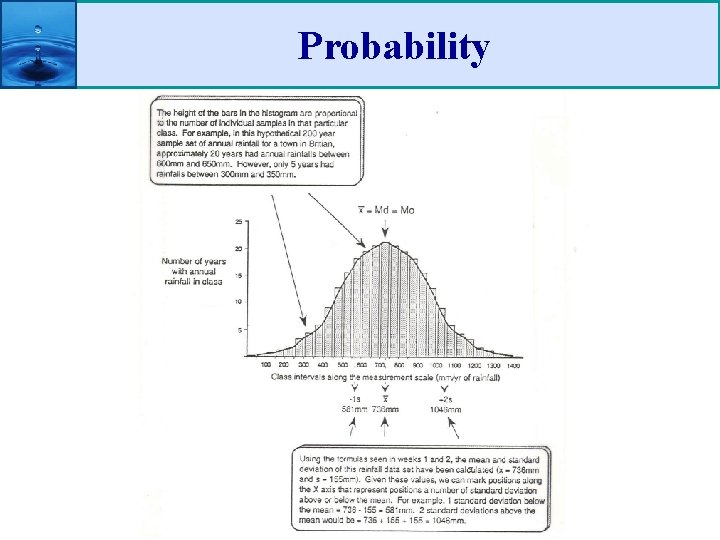
Statistics in Hydrology • Mean, median and mode (central tendency) • Dispersion: the spread of the items in a data set around its central value

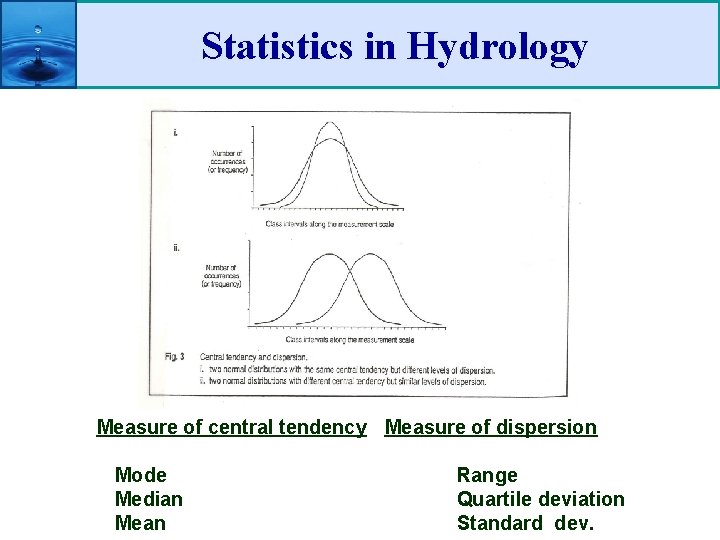
Statistics in Hydrology Measure of central tendency Measure of dispersion Mode Range Median Quartile deviation Mean Standard dev.

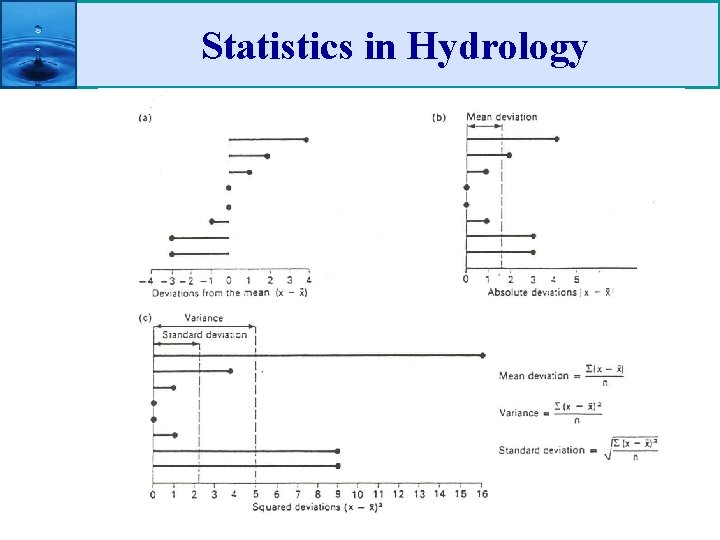
Statistics in Hydrology

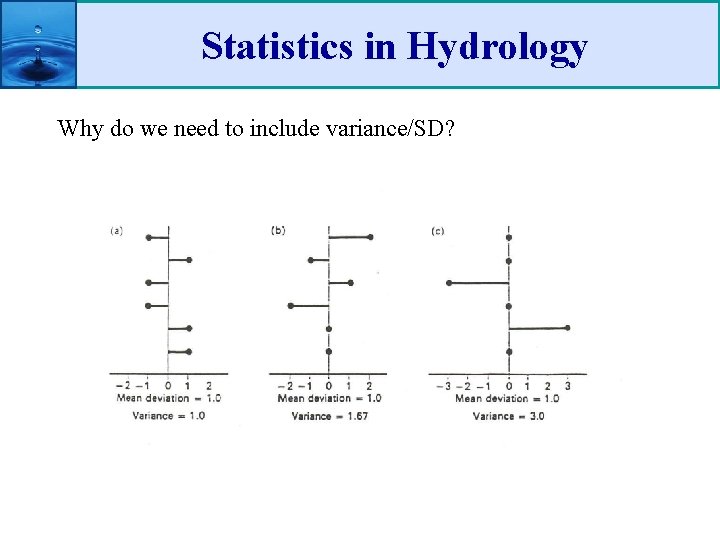
Statistics in Hydrology Why do we need to include variance/SD?

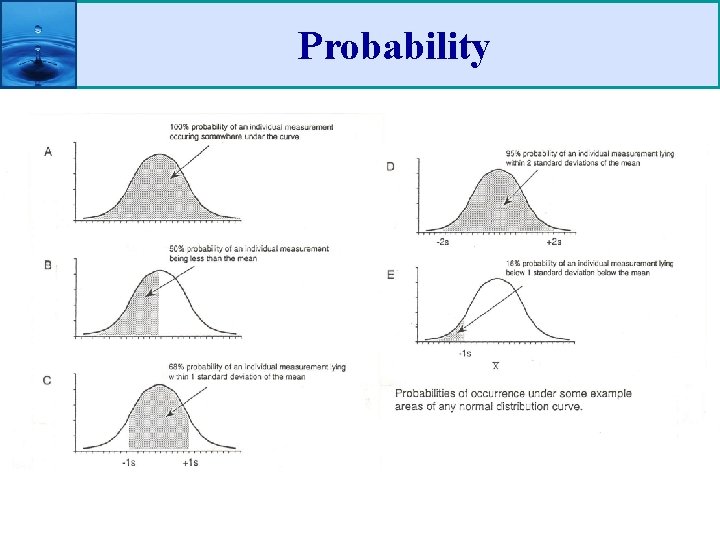
Probability • We need to know its probability of occurrence (the level of peak Q likely to occur/100 years (moving to inferential stats)

Probability

Probability

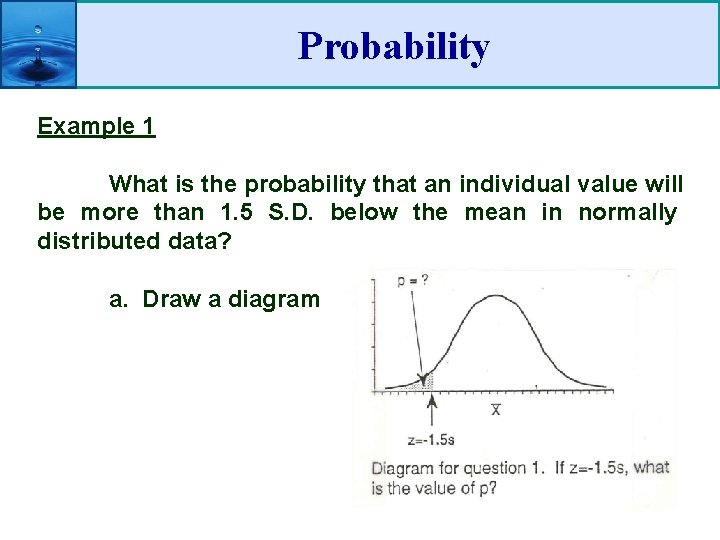
Probability Example 1 What is the probability that an individual value will be more than 1. 5 S. D. below the mean in normally distributed data? a. Draw a diagram

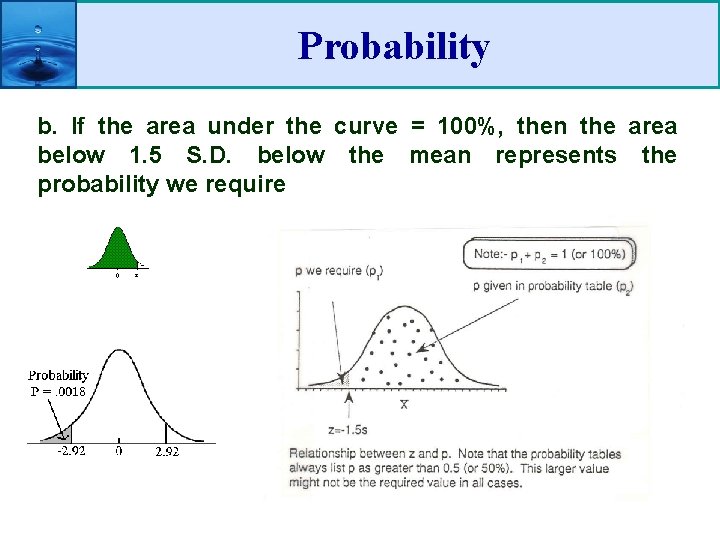
Probability b. If the area under the curve = 100%, then the area below 1. 5 S. D. below the mean represents the probability we require

Probability

Probability c. With z = 1. 5 then p = 0. 9932%. Look at the table again! It lists p values > 50% (not always required value); be careful!

Probability d. the probability we require is 1 - 0. 9332 = 0. 0668 e. The probability that an individual value will be more than 1. 5 S. D. below the mean in the data set is 6. 68% At home: What is the probability of getting less than 500 mm of rainfall in any one year in Edinburgh, Scotland given a mean annual rainfall of 664 mm and a S. D. of 120 mm?

Risk = probability * consequence

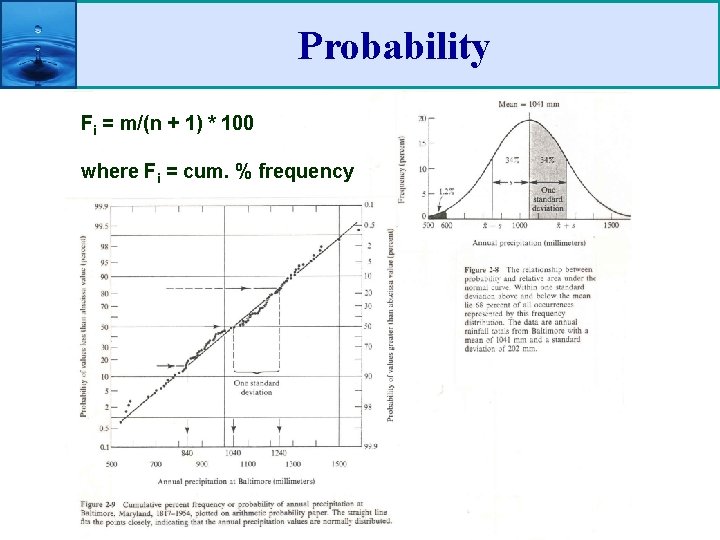
Probability Fi = m/(n + 1) * 100 where Fi = cum. % frequency

Hypothesis Testing • Sampling from a larger population Null hypothesis: no significant difference between the figures (H 0) Alternative hypothesis: is a significant difference between the figures (H 1) • Level of significance (0. 05 and 0. 01)

Hypothesis Testing Daily Q: Mean = 200 l/day S. D. = 30 l/day Sample = 128 litres SD = 30 * 1. 96 = 58. 8 L 95% of obs. should lie between 141. 2 and 258. 8 L

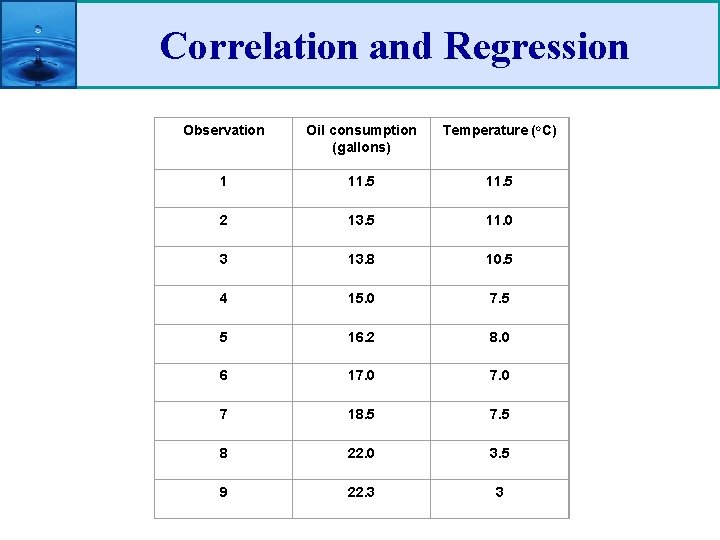
Correlation and Regression Observation Oil consumption (gallons) Temperature (o. C) 1 11. 5 2 13. 5 11. 0 3 13. 8 10. 5 4 15. 0 7. 5 5 16. 2 8. 0 6 17. 0 7 18. 5 7. 5 8 22. 0 3. 5 9 22. 3 3

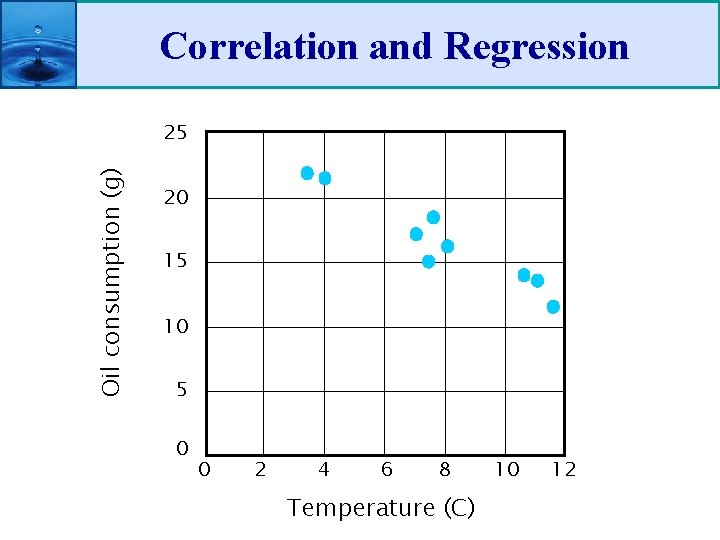
Correlation and Regression Oil consumption (g) 25 20 15 10 5 0 0 2 4 6 8 Temperature (C) 10 12

Correlation and Regression Correlation coefficient (r) Coefficient of determination (r 2) Lies between 0 and 1 Proportion of variation of Y associated with variations in X r = 0. 96; r 2 = 0. 92

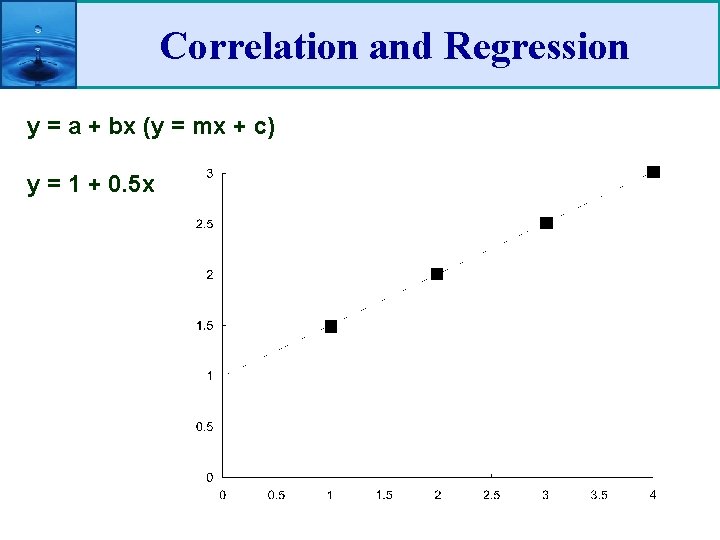
Correlation and Regression y = a + bx (y = mx + c) y = 1 + 0. 5 x

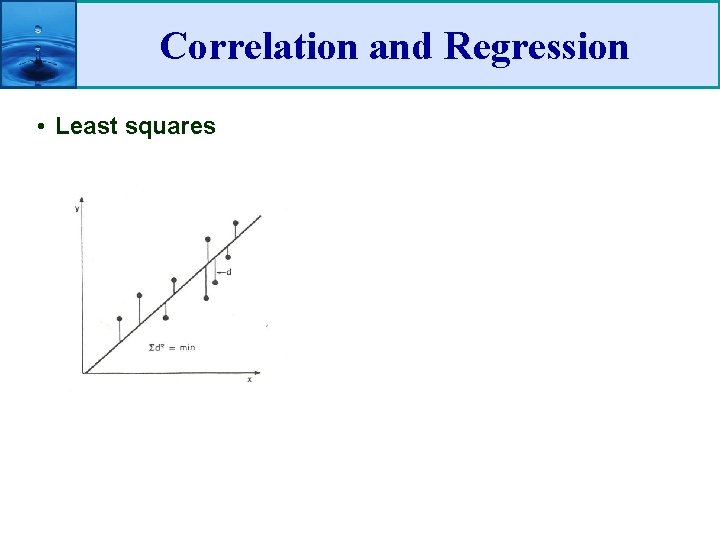
Correlation and Regression • Least squares

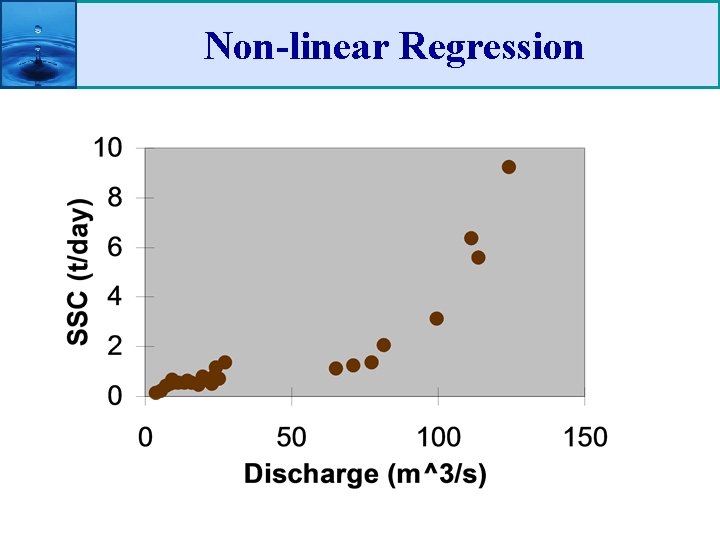
Non-linear Regression

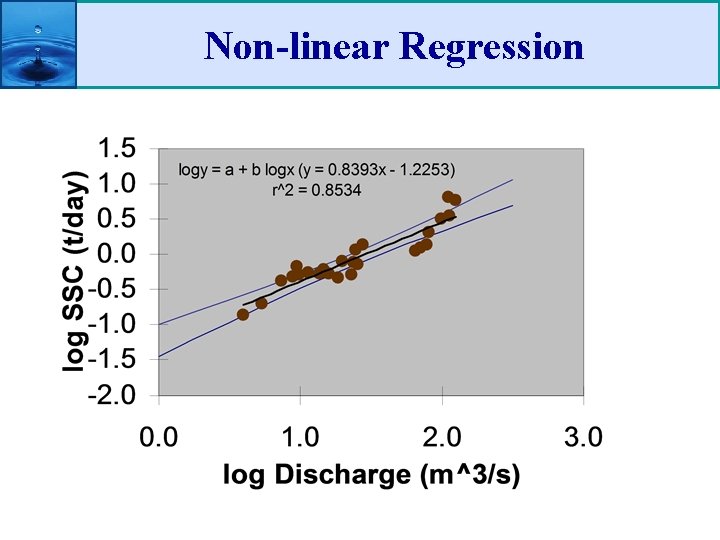
Non-linear Regression

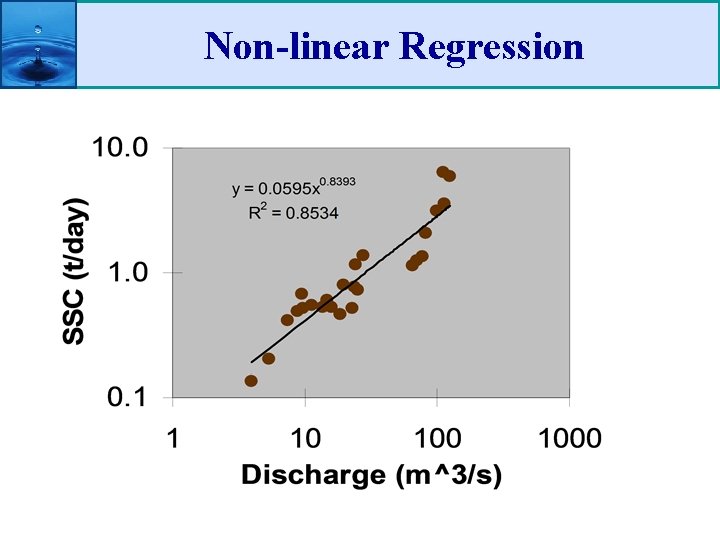
Non-linear Regression