Statistics for Water Science Hypothesis Testing Fundamental concepts

Statistics for Water Science: Hypothesis Testing: Fundamental concepts and a survey of methods Unite 5: Module 17, Lecture 2

Statistics · A branch of mathematics dealing with the collection, analysis, interpretation and presentation of masses of numerical data: · Descriptive Statistics (Lecture 1) · Basic description of a variable · Hypothesis Testing (Lecture 2) · Asks the question – is X different from Y? · Predictions (Lecture 3) · What will happen if… Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 2

Objectives · Introduce the basic concepts and assumptions of significance tests · Distributions on parade · Developing hypotheses · What is “true”? · Survey statistical methods for testing for differences in populations of numbers · Sample size issues · Appropriate tests · What we won’t do: · Elaborate on mathematical underpinnings of tests (take a good stats course for this!) Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 3

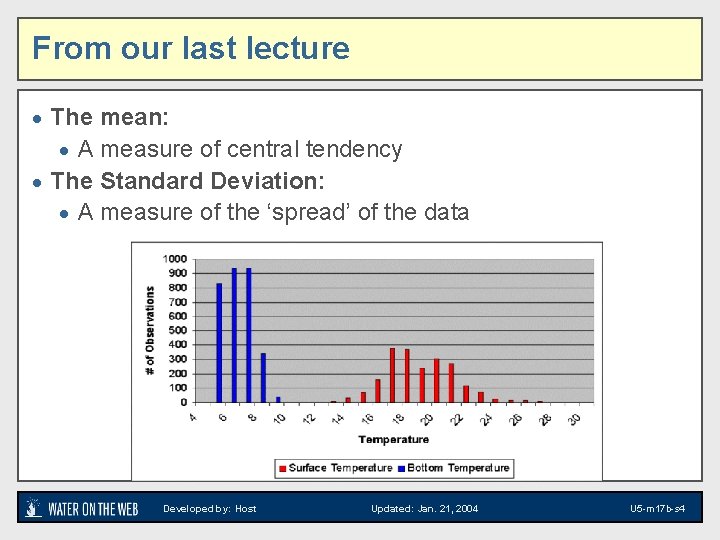
From our last lecture · The mean: · A measure of central tendency · The Standard Deviation: · A measure of the ‘spread’ of the data Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 4

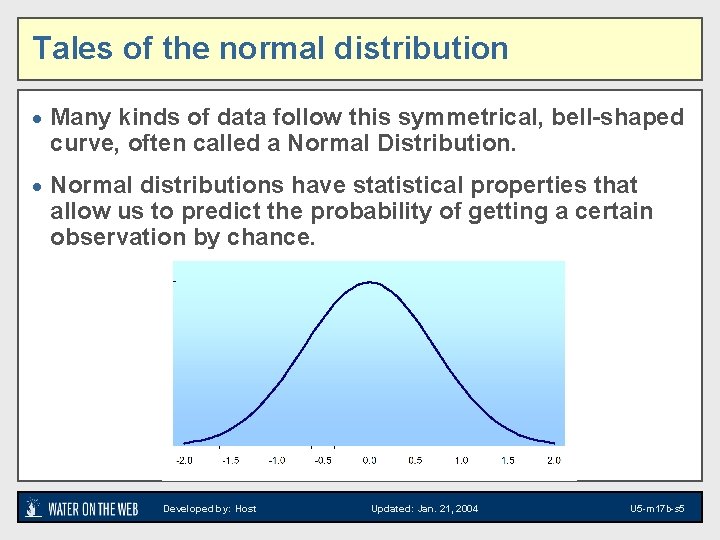
Tales of the normal distribution · Many kinds of data follow this symmetrical, bell-shaped curve, often called a Normal Distribution. · Normal distributions have statistical properties that allow us to predict the probability of getting a certain observation by chance. Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 5

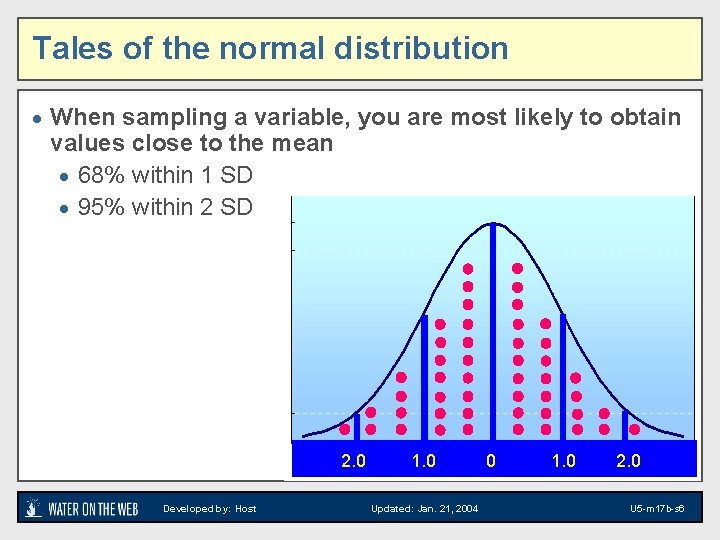
Tales of the normal distribution · When sampling a variable, you are most likely to obtain values close to the mean · 68% within 1 SD · 95% within 2 SD 2. 0 Developed by: Host 1. 0 Updated: Jan. 21, 2004 0 1. 0 2. 0 U 5 -m 17 b-s 6

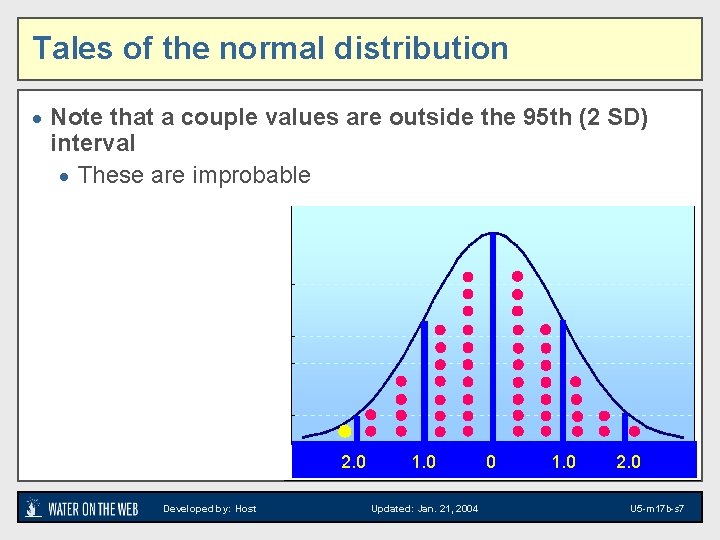
Tales of the normal distribution · Note that a couple values are outside the 95 th (2 SD) interval · These are improbable 2. 0 Developed by: Host 1. 0 Updated: Jan. 21, 2004 0 1. 0 2. 0 U 5 -m 17 b-s 7

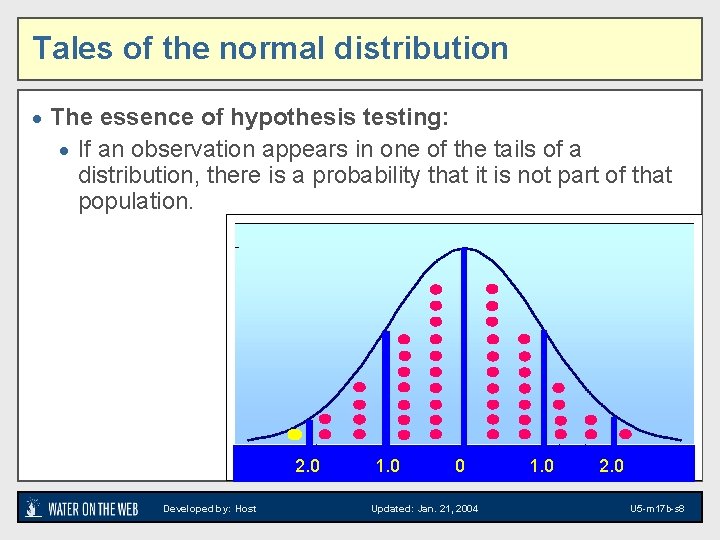
Tales of the normal distribution · The essence of hypothesis testing: · If an observation appears in one of the tails of a distribution, there is a probability that it is not part of that population. 2. 0 Developed by: Host 1. 0 0 Updated: Jan. 21, 2004 1. 0 2. 0 U 5 -m 17 b-s 8

“Significant Differences” · A difference is considered significant if the probability of getting that difference by random chance is very small. · P value: · The probability of making an error by chance · Historically we use p < 0. 05 Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 9

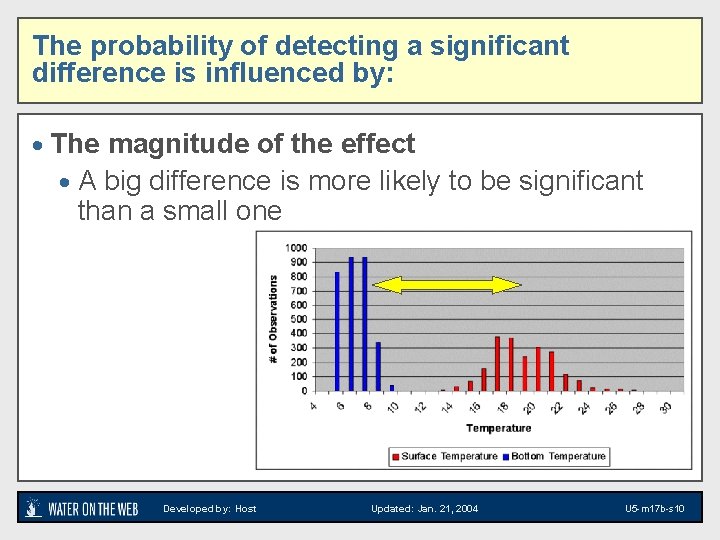
The probability of detecting a significant difference is influenced by: · The magnitude of the effect · A big difference is more likely to be significant than a small one Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 10

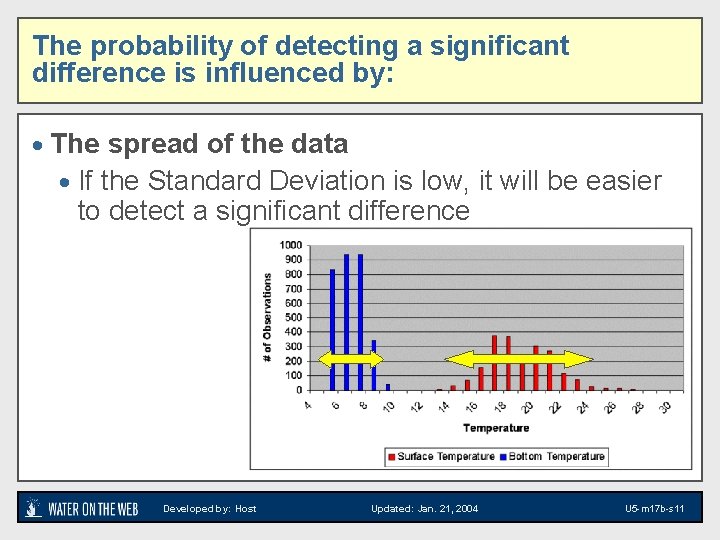
The probability of detecting a significant difference is influenced by: · The spread of the data · If the Standard Deviation is low, it will be easier to detect a significant difference Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 11

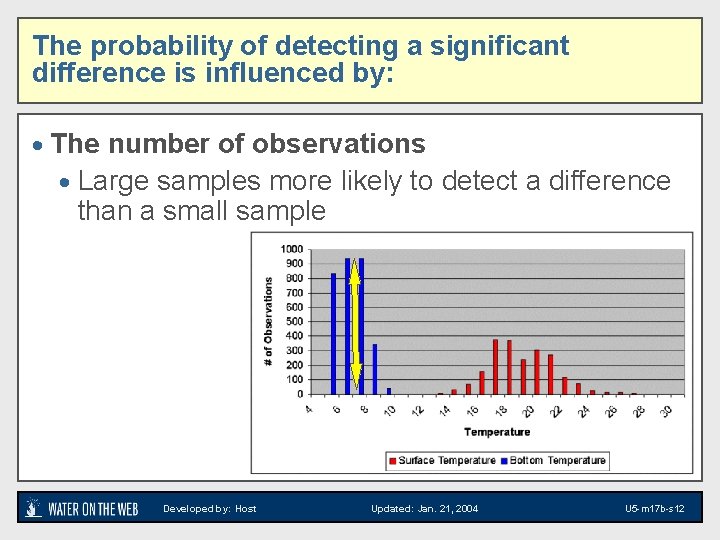
The probability of detecting a significant difference is influenced by: · The number of observations · Large samples more likely to detect a difference than a small sample Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 12

Hypothesis testing · Hypothesis: · A statement which can be proven false · Null hypothesis HO: · “There is no difference” · Alternative hypothesis (HA): · “There is a difference…” · In statistical testing, we try to “reject the null hypothesis” · If the null hypothesis is false, it is likely that our alternative hypothesis is true · “False” – there is only a small probability that the results we observed could have occurred by chance Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 13

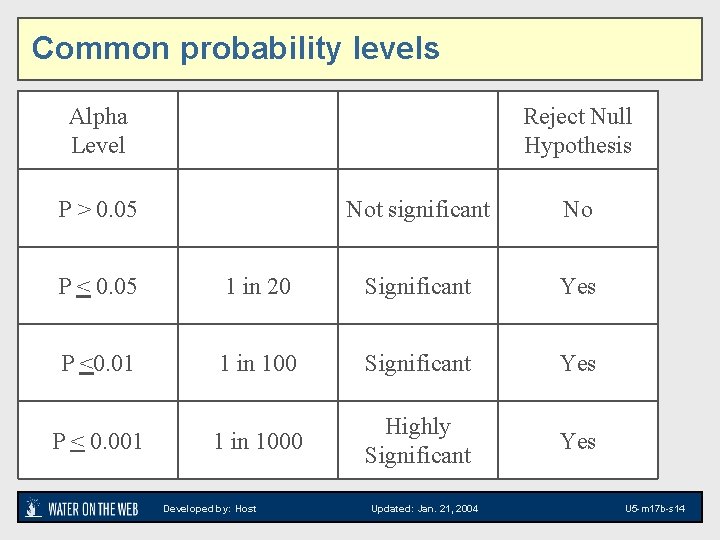
Common probability levels Alpha Level Reject Null Hypothesis P > 0. 05 Not significant No P < 0. 05 1 in 20 Significant Yes P <0. 01 1 in 100 Significant Yes 1 in 1000 Highly Significant Yes P < 0. 001 Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 14

Types of statistical errors (you could be right, you could be wrong) Accept Ho Reject Ho Ho is True Correct Decision Type I Error Alpha Ho is False Type II Error Beta Correct Decision Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 15

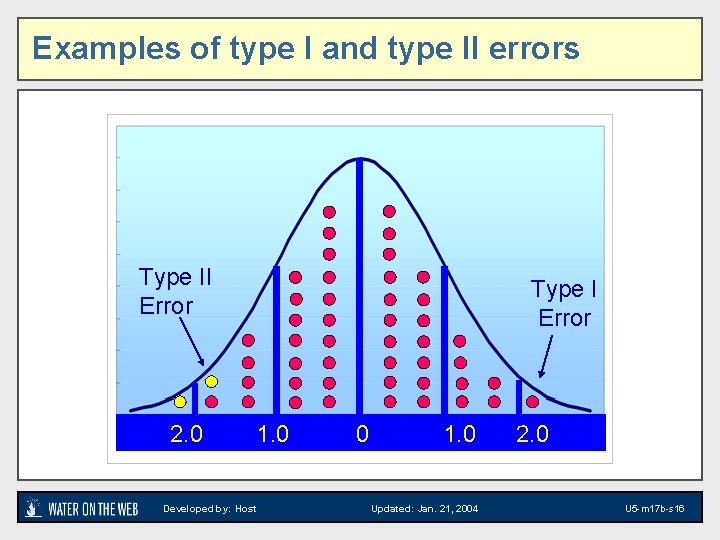
Examples of type I and type II errors Type II Error 2. 0 Type I Error 1. 0 Developed by: Host 0 1. 0 Updated: Jan. 21, 2004 2. 0 U 5 -m 17 b-s 16

Common statistical tests Question Test Does a single observation belong to a population of values? Are two (or more populations) of number different? Z-test T-test F-test (ANOVA) Is there a relationship between x and y Regression Is there a trend in the data (special case of above Regression Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 17

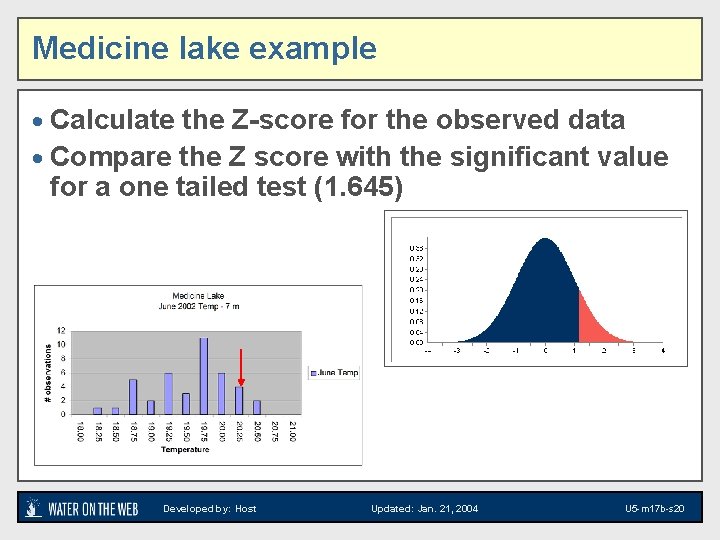
Does a single observation belong to a population of values: The Z-test · On June 26, 2002, a temperature probe reading at 7 m depth in Medicine Lake was 20. 30 C. Is this unusually high for June? Note: this is a “one-tailed test”, we just want to know if it’s high We’re not asking if it is unusually low or high (2 tailed) Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 18

The z distribution: Standard normal distribution) · The Z-distribution is a Normal Distribution, with special properties: · Mean = 0 Variance = 1 · Z = (observed value – mean)/standard error · Standard error = standard deviation * sqrt(n) The Z distribution Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 19

Medicine lake example · Calculate the Z-score for the observed data · Compare the Z score with the significant value for a one tailed test (1. 645) Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 20

The Deep Math… Z = (observed value – mean)/standard error Standard error = standard deviation * sqrt(n) Z = (20. 3 – 19. 7) 0. 08 = 6. 89 · Since 6. 89 > the critical Z value of 1. 64 · Our deep temperature is significantly higher than the June average temperature. · Further exploration shows that a storm the previous day caused the warmer surface waters to mix into the deeper waters. Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 21

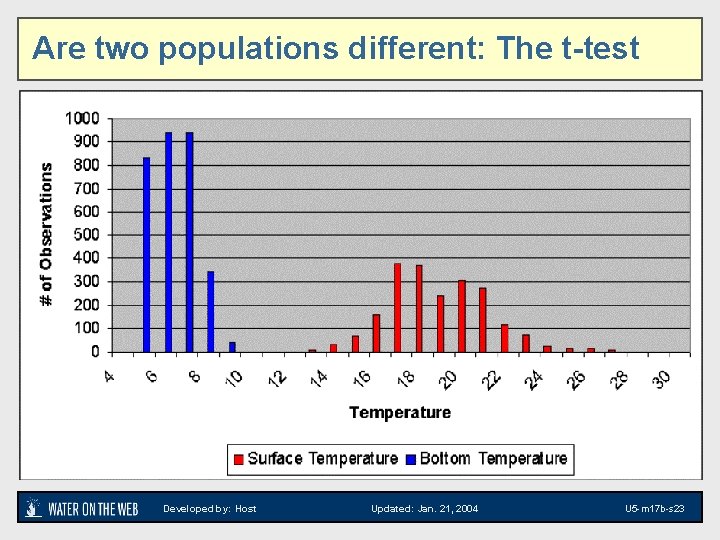
Are two populations different: The t-test · Also called Student’s t-test. “Student” was a synonym for a statistician that worked for Guinness brewery · Useful for “small” samples (<30) · One of the most basic statistical tests, can be performed in Excel or any common statistical package Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 22

Are two populations different: The t-test Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 23

Are two populations different: The t-test · One of the most basic statistical tests, can be performed in Excel or any common statistical package · Same principle as Z-test – calculate a t value, and assess the probability of getting that value Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 24

In Excel · Formula: · @ttest(Pop 1, Pop 2, #Tails, Test. Type) · Tailed tests: 1 or 2 · Test. Type · 1 - paired (if there is a logical pairing of XY data) · 2 - equal variance · 3 - unequal variance · Test returns exact probability value Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 25

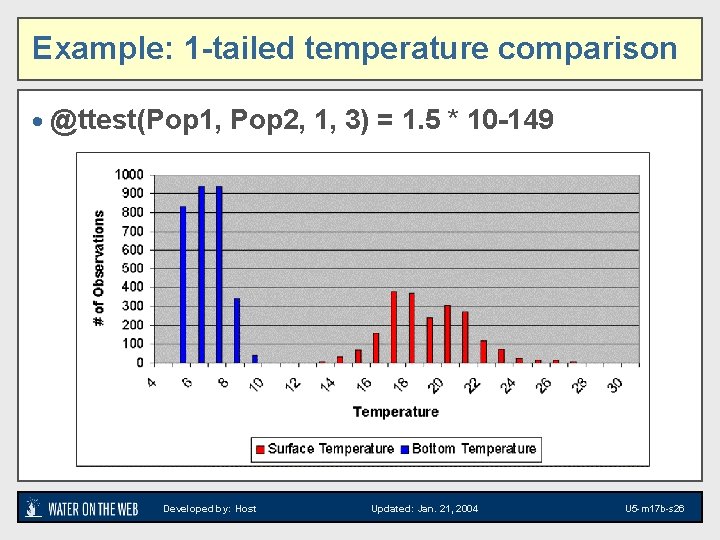
Example: 1 -tailed temperature comparison · @ttest(Pop 1, Pop 2, 1, 3) = 1. 5 * 10 -149 Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 26

ANOVA: Tests of multiple populations · ANOVA – analysis of variance · Compare 2 or more populations · Surface temperatures for 3 lakes · Can handle single or multiple factors · One way ANOVA – comparing lakes · Two-way ANOVA – compare two factors · Temperature x Light effects on algal populations · Repeated measures ANOVA – compare factors over time Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 27

Next Time: Regression - Finding relationships among variables Developed by: Host Updated: Jan. 21, 2004 U 5 -m 17 b-s 28