Statistics for Microarrays Experimental Design and Differential Expression

Statistics for Microarrays Experimental Design and Differential Expression Class web site: http: //statwww. epfl. ch/davison/teaching/Microarrays/ETHZ/

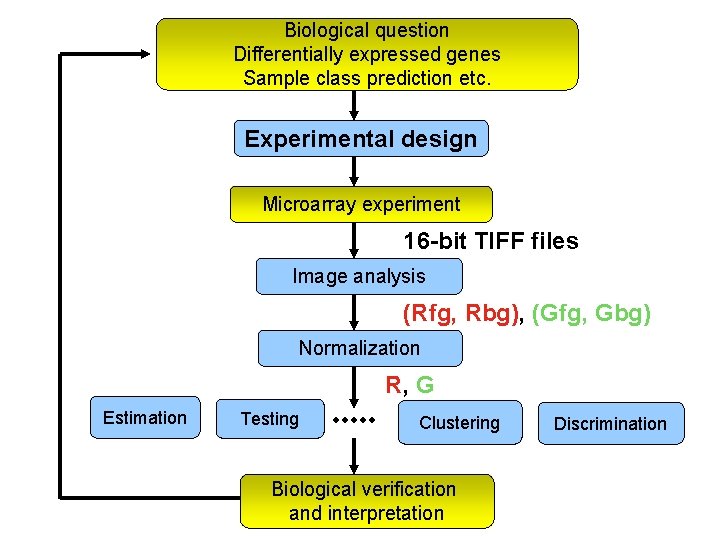
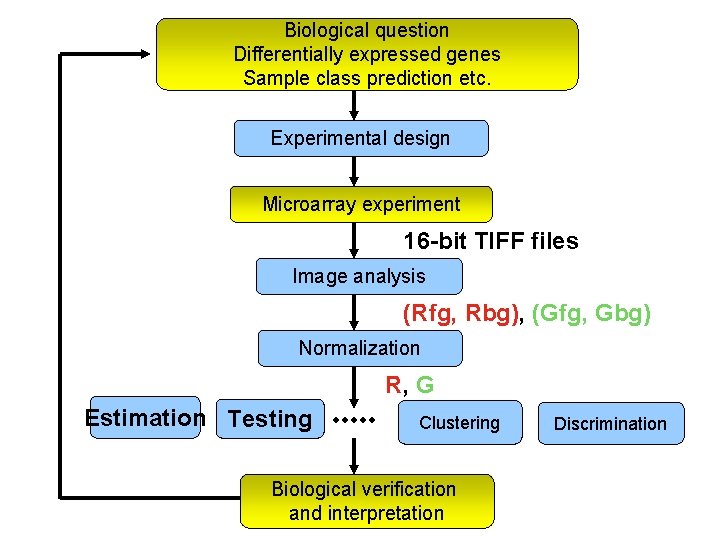
Biological question Differentially expressed genes Sample class prediction etc. Experimental design Microarray experiment 16 -bit TIFF files Image analysis (Rfg, Rbg), (Gfg, Gbg) Normalization R, G Estimation Testing Clustering Biological verification and interpretation Discrimination

Some Considerations for c. DNA Microarray Experiments (I) Scientific (Aims of the experiment) • Specific questions and priorities • How will the experiments answer the questions Practical (Logistic) • Types of m. RNA samples: reference, control, treatment, mutant, etc • Source and Amount of material (tissues, cell lines) • Number of slides available

Some Considerations for c. DNA Microarray Experiments (II) Other Information • Experimental process prior to hybridization: sample isolation, m. RNA extraction, amplification, labelling, … • Controls planned: positive, negative, ratio, etc. • Verification method: Northern, RT-PCR, in situ hybridization, etc.

Aspects of Experimental Design Applied to Microarrays (I) Array Layout • Which c. DNA sequences are printed • Spatial position Allocation of samples to slides • Design layouts • A vs B: Treatment vs control • Multiple treatments • Factorial • Time series

Aspects of Experimental Design Applied to Microarrays (II) Other considerations • Replication • Physical limitations: the number of slides and the amount of material • Sample Size • Extensibility - linking

Layout options The main issue is the use of reference samples, typically labelled green. Standard statistical design principles can lead to more efficient layouts; use of dye -swaps can also help. Sample size determination is more than usually difficult, as there are 1, 000 s of possible changes, each with its own SD.

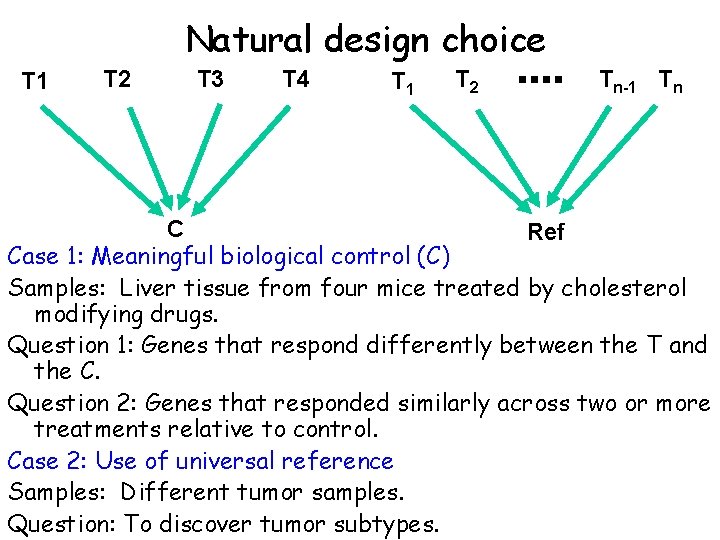
Natural design choice T 1 T 2 T 3 T 4 T 1 T 2 Tn-1 Tn C Ref Case 1: Meaningful biological control (C) Samples: Liver tissue from four mice treated by cholesterol modifying drugs. Question 1: Genes that respond differently between the T and the C. Question 2: Genes that responded similarly across two or more treatments relative to control. Case 2: Use of universal reference Samples: Different tumor samples. Question: To discover tumor subtypes.

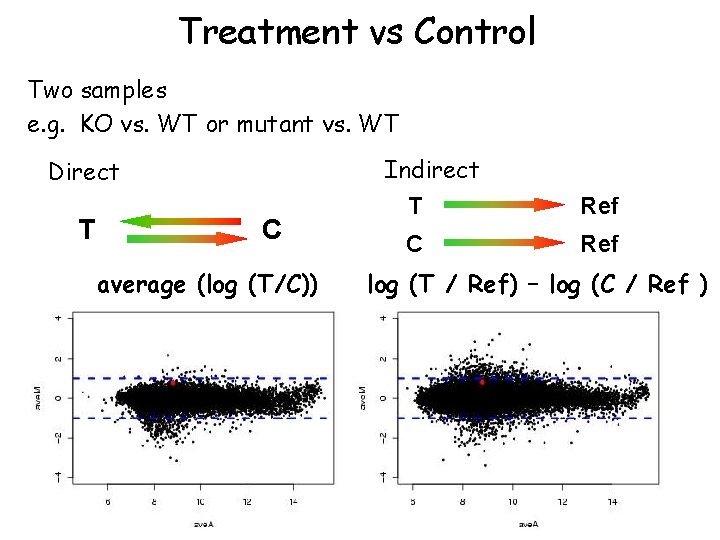
Treatment vs Control Two samples e. g. KO vs. WT or mutant vs. WT Indirect Direct T C average (log (T/C)) 2 /2 T Ref C Ref log (T / Ref) – log (C / Ref ) 2 2

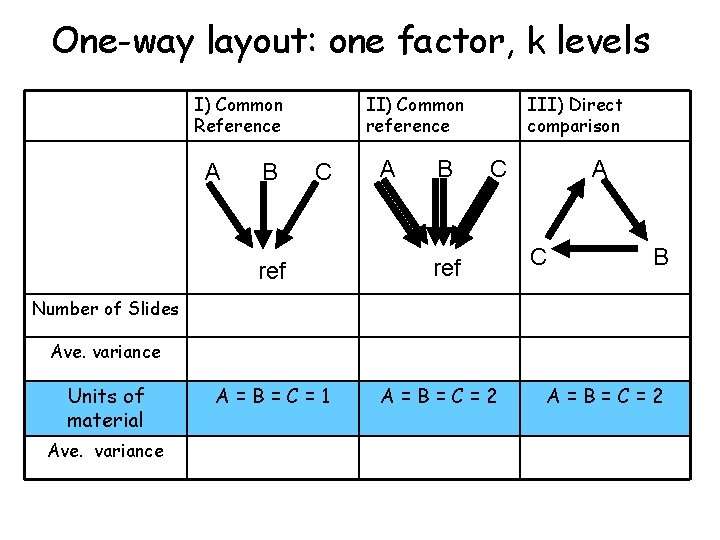
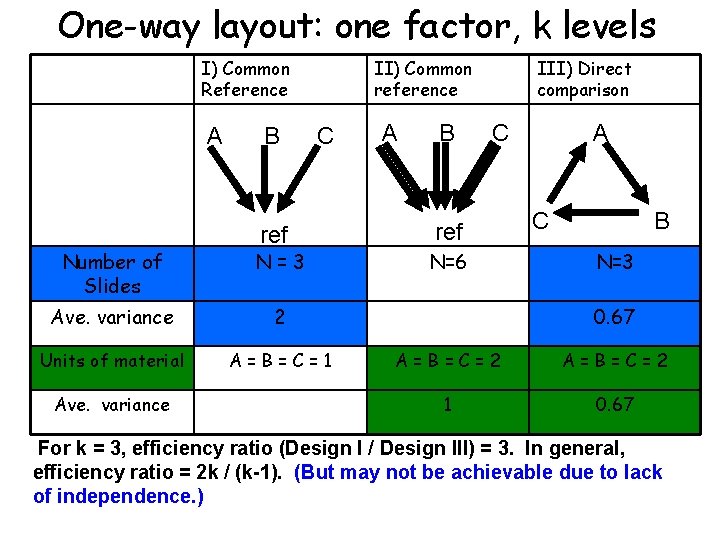
One-way layout: one factor, k levels I) Common Reference A B II) Common reference C ref A B III) Direct comparison C ref A C B Number of Slides Ave. variance Units of material Ave. variance A=B=C=1 A=B=C=2

One-way layout: one factor, k levels I) Common Reference A B II) Common reference C ref Number of Slides N=3 Ave. variance 2 Units of material A=B=C=1 Ave. variance A B III) Direct comparison C ref N=6 A C B N=3 0. 67 A=B=C=2 1 0. 67 For k = 3, efficiency ratio (Design I / Design III) = 3. In general, efficiency ratio = 2 k / (k-1). (But may not be achievable due to lack of independence. )

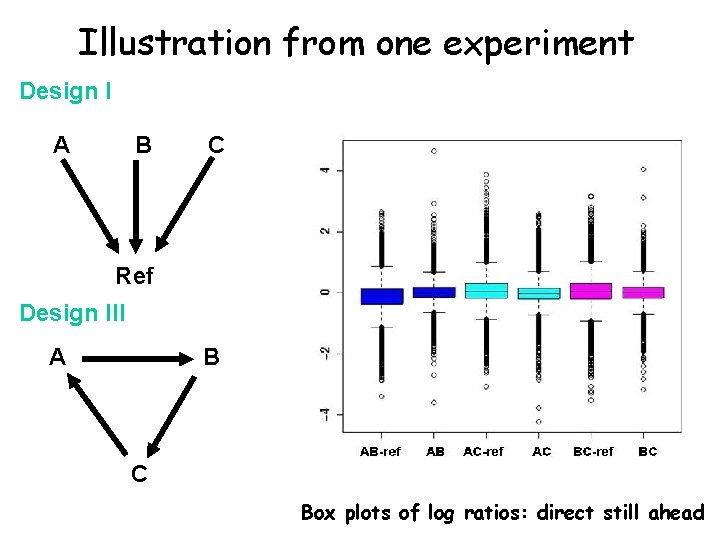
Illustration from one experiment Design I A B C Ref Design III A B C Box plots of log ratios: direct still ahead

Factorial experiments • Treated cell lines CTL OSM EGF OSM & EGF • Possible experiments Here interest is not in genes for which there is an O or an E (main) effect, but in which there is an O E interaction, i. e. in genes for which log(O&E/O)-log(E/C) is large or small.

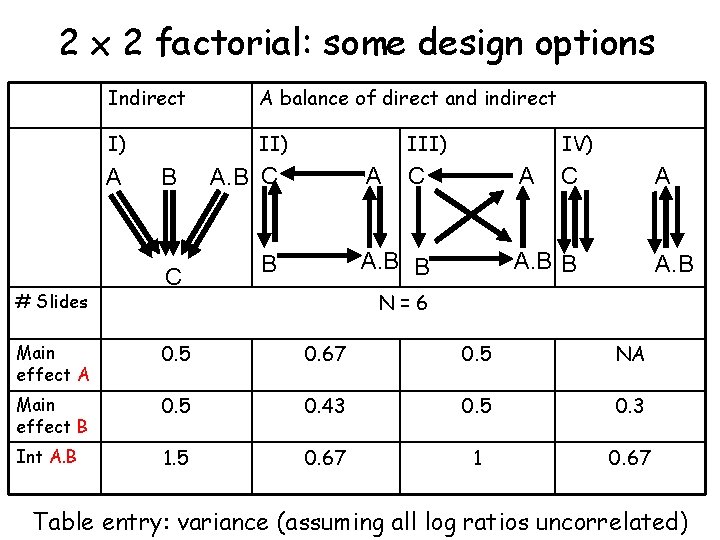
2 x 2 factorial: some design options Indirect A balance of direct and indirect I) II) A # Slides B C III) A. B C A IV) C A A. B B B C A A. B B A. B N=6 Main effect A 0. 5 0. 67 0. 5 NA Main effect B 0. 5 0. 43 0. 5 0. 3 Int A. B 1. 5 0. 67 1 0. 67 Table entry: variance (assuming all log ratios uncorrelated)

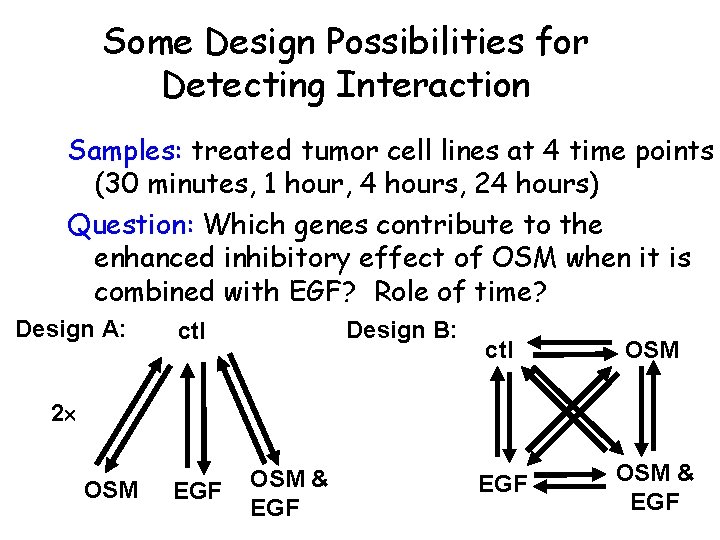
Some Design Possibilities for Detecting Interaction Samples: treated tumor cell lines at 4 time points (30 minutes, 1 hour, 4 hours, 24 hours) Question: Which genes contribute to the enhanced inhibitory effect of OSM when it is combined with EGF? Role of time? Design A: Design B: ctl OSM EGF OSM & EGF 2 OSM EGF OSM & EGF

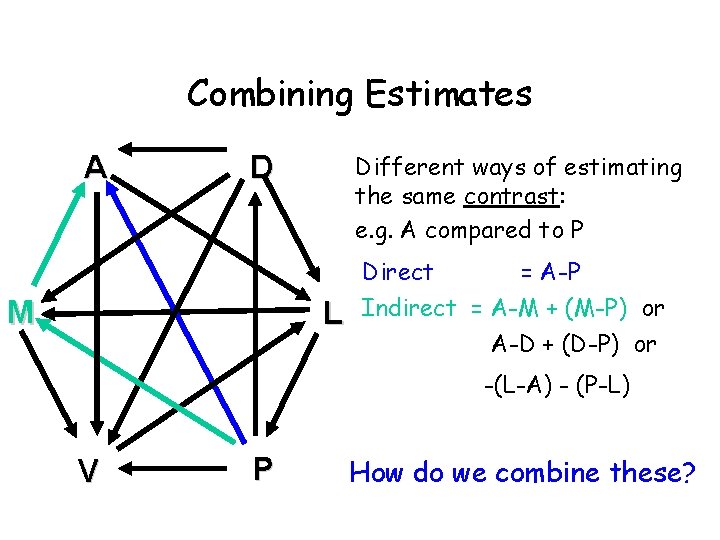
Combining Estimates A D M Different ways of estimating the same contrast: e. g. A compared to P L Direct = A-P Indirect = A-M + (M-P) or A-D + (D-P) or -(L-A) - (P-L) V P How do we combine these?

Time Course Experiments • Number of time points • Which differences are of highest interest (e. g. between initial time and later times, between adjacent times) • Number of slides available

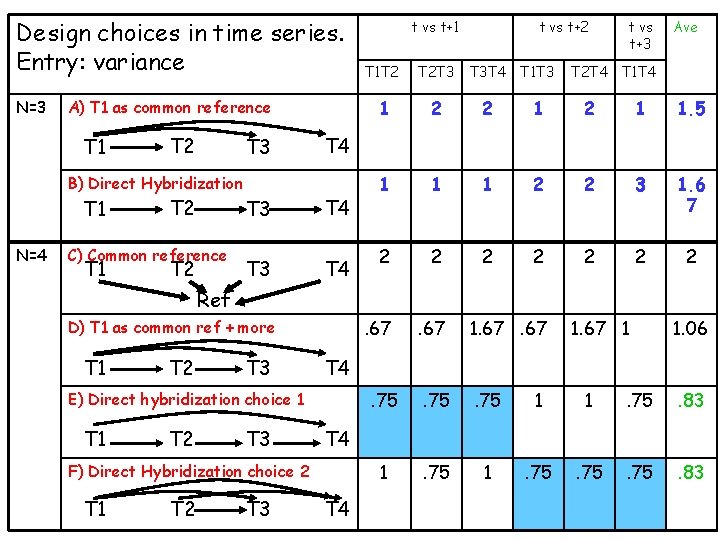
Design choices in time series. Entry: variance N=3 A) T 1 as common reference T 1 T 2 T 3 B) Direct Hybridization T 1 N=4 T 2 C) Common reference T 1 T 2 t vs t+1 t vs t+2 t vs t+3 Ave T 1 T 2 T 2 T 3 T 3 T 4 T 1 T 3 T 2 T 4 T 1 T 4 1 2 2 1 1. 5 1 1 1 2 2 3 1. 6 7 2 2 2 2 . 67 1. 67 . 75 1 1 . 75 . 83 1 . 75 . 83 T 4 T 3 T 4 Ref D) T 1 as common ref + more T 1 T 2 T 3 T 4 F) Direct Hybridization choice 2 T 1 T 2 T 3 1. 06 T 4 E) Direct hybridization choice 1 T 1 1. 67 1 T 4

Replication • Why? • To reduce variability • To increase generalizability • What is it? • Duplicate spots • Duplicate slides • Technical replicates • Biological replicates

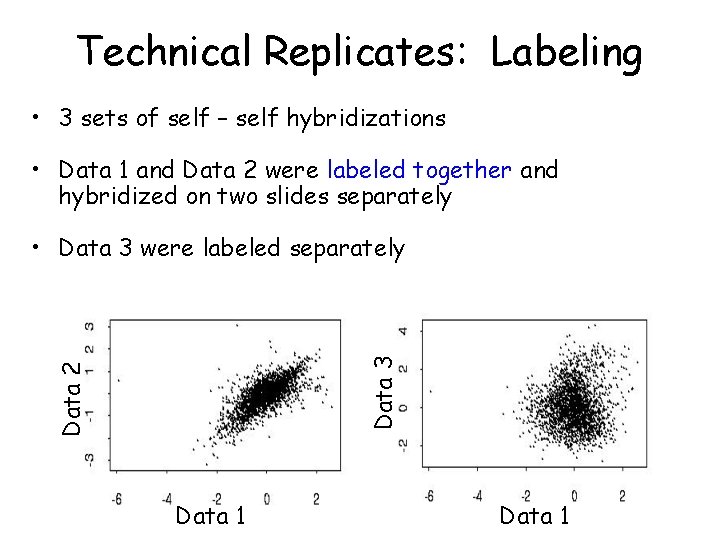
Technical Replicates: Labeling • 3 sets of self – self hybridizations • Data 1 and Data 2 were labeled together and hybridized on two slides separately Data 2 Data 3 • Data 3 were labeled separately Data 1

Sample Size • • Variance of individual measurements (X) Effect size(s) to be detected (X) Acceptable false positive rate Desired power (probability of detecting an effect of at least the specfied size)

Extensibility • “Universal” common reference for arbitrary undetermined number of (future) experiments • Provides extensibility of the series of experiments (within and between labs) • Linking experiments necessary if common reference source diminished/depleted

Summary • Balance of direct and indirect comparisons • Optimize precision of the estimates among comparisons of interest • Must satisfy scientific and physical constraints of the experiment

Identifying Differentially Expressed Genes • Goal: Identify genes associated with covariate or response of interest • Examples: – Qualitative covariates or factors: treatment, cell type, tumor class – Quantitative covariate: dose, time – Responses: survival, cholesterol level – Any combination of these!

Biological question Differentially expressed genes Sample class prediction etc. Experimental design Microarray experiment 16 -bit TIFF files Image analysis (Rfg, Rbg), (Gfg, Gbg) Normalization R, G Estimation Testing Clustering Biological verification and interpretation Discrimination

Differentially Expressed Genes • Simultaneously test m null hypotheses, one for each gene j : Hj: no association between expression level of gene j and covariate/response • Combine expression data from different slides and estimate effects of interest • Compute test statistic Tj for each gene j • Adjust for multiple hypothesis testing

Test statistics • Qualitative covariates: e. g. two-sample tstatistic, Mann-Whitney statistic, Fstatistic • Quantitative covariates: e. g. standardized regression coefficient • Survival response: e. g. score statistic for Cox model

Example: Apo AI experiment (Callow et al. , Genome Research, 2000) GOAL: Identify genes with altered expression in the livers of one line of mice with very low HDL cholesterol levels compared to inbred control mice Experiment: • Apo AI knock-out mouse model • 8 knockout (ko) mice and 8 control (ctl) mice (C 57 Bl/6) • 16 hybridisations: m. RNA from each of the 16 mice is labelled with Cy 5, pooled m. RNA from control mice is labelled with Cy 3 Probes: ~6, 000 c. DNAs, including 200 related to lipid metabolism

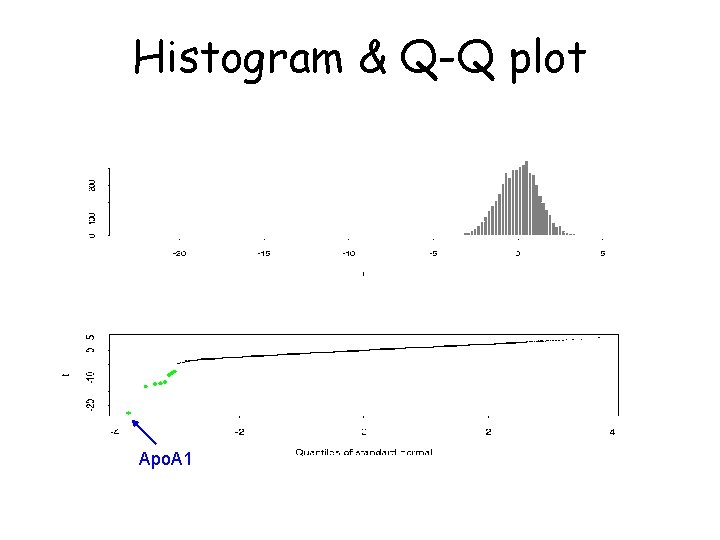
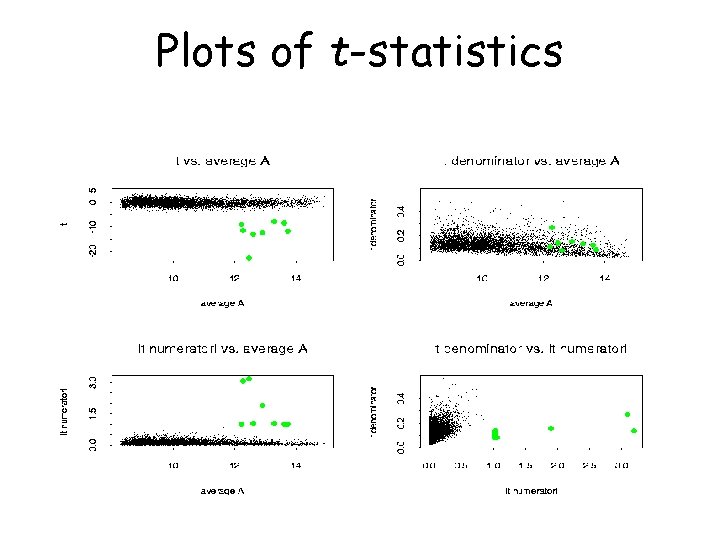
Which genes have changed? This method can be used with replicated data: 1. For each gene and each hybridisation (8 ko + 8 ctl) use M=log 2(R/G) 2. For each gene form the t-statistic: average of 8 ko Ms - average of 8 ctl Ms sqrt(1/8 (SD of 8 ko Ms)2 + 1/8 (SD of 8 ctl Ms)2) 3. Form a histogram of 6, 000 t values 4. Make a normal Q-Q plot; look for values “off the line” 5. Adjust for multiple testing

Histogram & Q-Q plot Apo. A 1

Plots of t-statistics

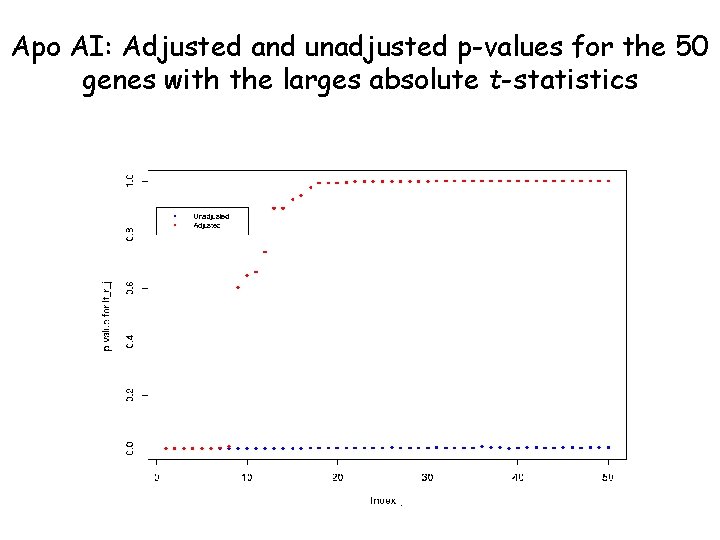
Assigning p-values to measures of change • Estimate p-values for each comparison (gene) by using the permutation distribution of the tstatistics. • For each of the possible permutation of the trt / ctl labels, compute the two-sample t-statistics t* for each gene. • The unadjusted p-value for a particular gene is estimated by the proportion of t*’s greater than the observed t in absolute value.

Apo AI: Adjusted and unadjusted p-values for the 50 genes with the larges absolute t-statistics

Genes with adjusted p-value 0. 01

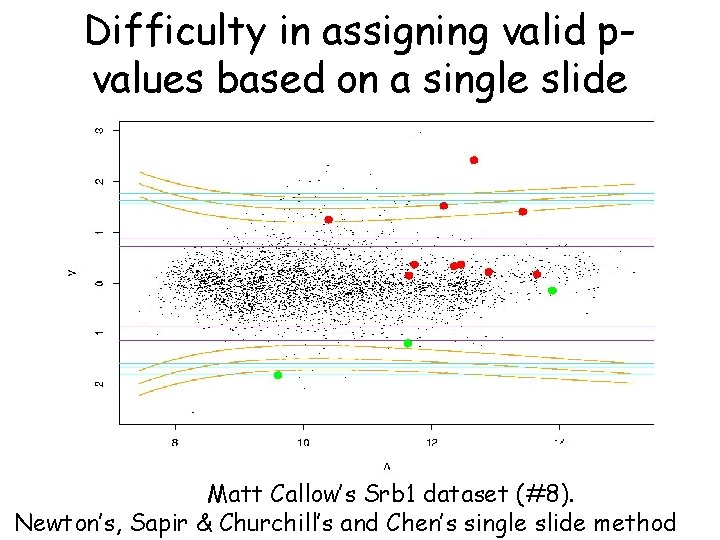
Single-slide methods • Model-dependent rules for deciding whether (R, G) corresponds to a differentially expressed gene • Amounts to drawing two curves in the (R, G)-plane; call a gene differentially expressed if it falls outside the region between the two curves • At this time, not enough known about the systematic and random variation within a microarray experiment to justify these strong modeling assumptions • n = 1 slide may not be enough (!)

Single-slide methods • Chen et al: Each (R, G) is assumed to be normally and independently distributed with constant CV; decision based on R/G only (purple) • Newton et al: Gamma-Bernoulli hierarchical model for each (R, G) (yellow) • Roberts et al: Each (R, G) is assumed to be normally and independently distributed with variance depending linearly on the mean • Sapir & Churchill: Each log R/G assumed to be distributed according to a mixture of normal and uniform distributions; decision based on R/G only (turquoise)

Difficulty in assigning valid pvalues based on a single slide Matt Callow’s Srb 1 dataset (#8). Newton’s, Sapir & Churchill’s and Chen’s single slide method

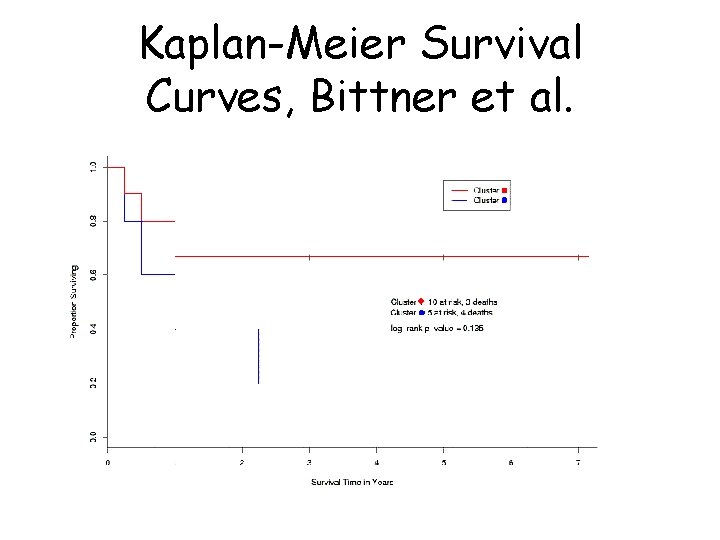
Another example: Survival analysis with expression data • Bittner et al. looked at differences in survival between the two groups (the ‘cluster’ and the ‘unclustered’ samples) • ‘Cluster’ seemed to have longer survival

Kaplan-Meier Survival Curves, Bittner et al.

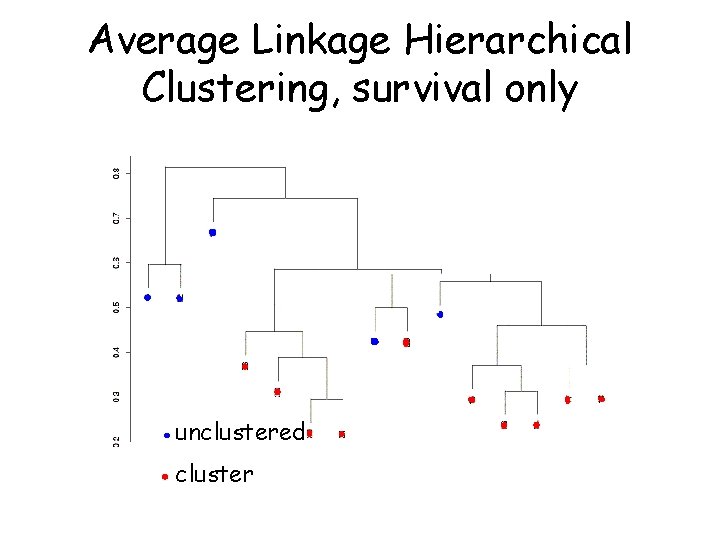
Average Linkage Hierarchical Clustering, survival only unclustered cluster

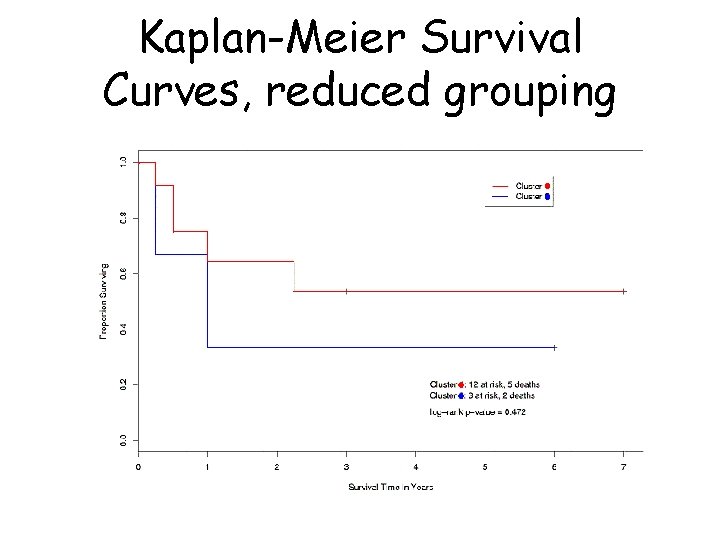
Kaplan-Meier Survival Curves, reduced grouping

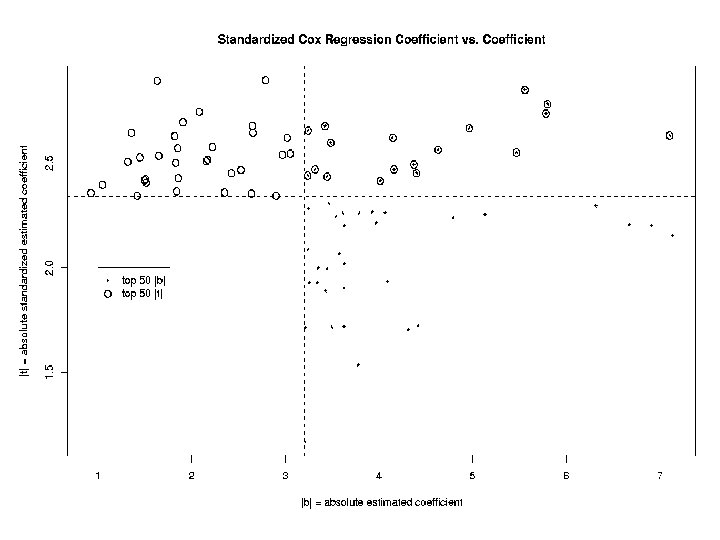
Identification of genes associated with survival For each gene j, j = 1, …, 3613, model the instantaneous failure rate, or hazard function, h(t) with the Cox proportional hazards model: h(t) = h 0(t) exp( jxij) and look for genes with both: ^ • large effect size j ^ ^ • large standardized effect size j/SE( j)

Findings • Top 5 genes by this method not in Bittner et al. ‘weighted gene list’ - Why? • weighted gene list based on entire sample; our method only used half • weighting relies on Bittner et al. cluster assignment • other possibilities?

Limitations of Single Gene Tests • May be too noisy in general to show much • Do not reveal coordinated effects of positively correlated genes • Hard to relate to pathways

Some ideas for further work • Expand models to include more genes and possibly two-way interactions • Nonparametric tree-based subset selection – would require much larger sample sizes

Acknowledgements • Sandrine Dudoit • Jane Fridlyand • Yee Hwa (Jean) Yang • Debashis Ghosh • Erin Conlon • Ingrid Lonnstedt • Terry Speed