Statistics for Managers Using Microsoft Excel 4 th

Statistics for Managers Using Microsoft® Excel 4 th Edition Chapter 10 Analysis of Variance Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. Chap 10 -1

Chapter Goals After completing this chapter, you should be able to: n Recognize situations in which to use analysis of variance n Understand different analysis of variance designs n Perform a single-factor hypothesis test and interpret results n n Conduct and interpret post-hoc multiple comparisons procedures Analyze two-factor analysis of variance tests Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 2

Chapter Overview Analysis of Variance (ANOVA) One-Way ANOVA F-test Two-Way ANOVA Interaction Effects Tukey. Kramer test Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 3

General ANOVA Setting n Investigator controls one or more independent variables n n n Observe effects on the dependent variable n n Called factors (or treatment variables) Each factor contains two or more levels (or groups or categories/classifications) Response to levels of independent variable Experimental design: the plan used to collect the data Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 4

Completely Randomized Design n Experimental units (subjects) are assigned randomly to treatments n n Only one factor or independent variable n n Subjects are assumed homogeneous With two or more treatment levels Analyzed by one-factor analysis of variance (one-way ANOVA) Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 5

One-Way Analysis of Variance n Evaluate the difference among the means of three or more groups Examples: Accident rates for 1 st, 2 nd, and 3 rd shift Expected mileage for five brands of tires n Assumptions n Populations are normally distributed n Populations have equal variances n Samples are randomly and independently drawn Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 6

Hypotheses of One-Way ANOVA n n n All population means are equal i. e. , no treatment effect (no variation in means among groups) n n At least one population mean is different n i. e. , there is a treatment effect n Does not mean that all population means are different (some pairs may be the same) Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 7

One-Factor ANOVA All Means are the same: The Null Hypothesis is True (No Treatment Effect) Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 8

One-Factor ANOVA (continued) At least one mean is different: The Null Hypothesis is NOT true (Treatment Effect is present) or Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 9

Partitioning the Variation n Total variation can be split into two parts: SST = SSA + SSW SST = Total Sum of Squares (Total variation) SSA = Sum of Squares Among Groups (Among-group variation) SSW = Sum of Squares Within Groups (Within-group variation) Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 10

Partitioning the Variation (continued) SST = SSA + SSW Total Variation = the aggregate dispersion of the individual data values across the various factor levels (SST) Among-Group Variation = dispersion between the factor sample means (SSA) Within-Group Variation = dispersion that exists among the data values within a particular factor level (SSW) Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 11

Partition of Total Variation (SST) = § § Variation Due to Factor (SSA) Variation Due to Random Sampling (SSW) + Commonly referred to as: Sum of Squares Between Sum of Squares Among Sum of Squares Explained Among Groups Variation Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. § § Commonly referred to as: Sum of Squares Within Sum of Squares Error Sum of Squares Unexplained Within Groups Variation 12

Total Sum of Squares SST = SSA + SSW Where: SST = Total sum of squares c = number of groups (levels or treatments) nj = number of observations in group j Xij = ith observation from group j X = grand mean (mean of all data values) Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 13

Total Variation (continued) Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 14

Among-Group Variation SST = SSA + SSW Where: SSA = Sum of squares among groups c = number of groups or populations nj = sample size from group j Xj = sample mean from group j X = grand mean (mean of all data values) Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 15

Among-Group Variation (continued) Variation Due to Differences Among Groups Mean Square Among = SSA/degrees of freedom Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 16

Among-Group Variation (continued) Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 17

Within-Group Variation SST = SSA + SSW Where: SSW = Sum of squares within groups c = number of groups nj = sample size from group j Xj = sample mean from group j Xij = ith observation in group j Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 18

Within-Group Variation (continued) Summing the variation within each group and then adding over all groups Mean Square Within = SSW/degrees of freedom Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 19

Within-Group Variation (continued) Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 20

Obtaining the Mean Squares Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 21

One-Way ANOVA Table Source of Variation SS df Among Groups SSA c-1 Within Groups SSW n-c Total SST = SSA+SSW n-1 MS (Variance) F ratio SSA MSA = c - 1 F = MSW SSW MSW = n-c c = number of groups n = sum of the sample sizes from all groups df = degrees of freedom Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 22

One-Factor ANOVA F Test Statistic H 0: μ 1= μ 2 = … = μ c H 1: At least two population means are different n Test statistic MSA is mean squares among variances MSW is mean squares within variances n Degrees of freedom n n df 1 = c – 1 df 2 = n – c (c = number of groups) (n = sum of sample sizes from all populations) Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 23

Interpreting One-Factor ANOVA F Statistic n The F statistic is the ratio of the among estimate of variance and the within estimate of variance n n n The ratio must always be positive df 1 = c -1 will typically be small df 2 = n - c will typically be large Decision Rule: n Reject H 0 if F > FU, otherwise do not reject H 0 Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. =. 05 0 Do not reject H 0 Reject H 0 FU 24

One-Factor ANOVA F Test Example You want to see if three different golf clubs yield different distances. You randomly select five measurements from trials on an automated driving machine for each club. At the. 05 significance level, is there a difference in mean distance? Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. Club 1 254 263 241 237 251 Club 2 234 218 235 227 216 Club 3 200 222 197 206 204 25

One-Factor ANOVA Example: Scatter Diagram Club 1 254 263 241 237 251 Club 2 234 218 235 227 216 Club 3 200 222 197 206 204 Distance 270 260 250 240 230 • • • 220 210 • • • • 200 190 1 Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. • 2 Club 3 26

One-Factor ANOVA Example Computations Club 1 254 263 241 237 251 Club 2 234 218 235 227 216 Club 3 200 222 197 206 204 X 1 = 249. 2 n 1 = 5 X 2 = 226. 0 n 2 = 5 X 3 = 205. 8 n 3 = 5 X = 227. 0 n = 15 c=3 SSA = 5 (249. 2 – 227)2 + 5 (226 – 227)2 + 5 (205. 8 – 227)2 = 4716. 4 SSW = (254 – 249. 2)2 + (263 – 249. 2)2 +…+ (204 – 205. 8)2 = 1119. 6 MSA = 4716. 4 / (3 -1) = 2358. 2 MSW = 1119. 6 / (15 -3) = 93. 3 Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 27

One-Factor ANOVA Example Solution Test Statistic: H 0: μ 1 = μ 2 = μ 3 H 1: μi not all equal =. 05 df 1= 2 df 2 = 12 Decision: Reject H 0 at = 0. 05 Critical Value: FU = 3. 89 =. 05 0 Do not reject H 0 Reject H 0 FU = 3. 89 Conclusion: There is evidence that at least one μi differs F = 25. 275 from the rest Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 28

ANOVA -- Single Factor: Excel Output EXCEL: tools | data analysis | ANOVA: single factor SUMMARY Groups Count Sum Average Variance Club 1 5 1246 249. 2 108. 2 Club 2 5 1130 226 77. 5 Club 3 5 1029 205. 8 94. 2 ANOVA Source of Variation SS df MS Between Groups 4716. 4 2 2358. 2 Within Groups 1119. 6 12 93. 3 Total 5836. 0 14 Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. F 25. 275 P-value 4. 99 E-05 F crit 3. 89 29

The Tukey-Kramer Procedure n Tells which population means are significantly different n n n e. g. : μ 1 = μ 2 μ 3 Done after rejection of equal means in ANOVA Allows pair-wise comparisons n Compare absolute mean differences with critical range μ 1= μ 2 Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. μ 3 x 30

Tukey-Kramer Critical Range where: QU = Value from Studentized Range Distribution with c and n - c degrees of freedom for the desired level of (see appendix E. 9 table) MSW = Mean Square Within ni and nj = Sample sizes from groups j and j’ Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 31

The Tukey-Kramer Procedure: Example Club 1 254 263 241 237 251 Club 2 234 218 235 227 216 Club 3 200 222 197 206 204 1. Compute absolute mean differences: 2. Find the QU value from the table in appendix E. 9 with c = 3 and (n – c) = (15 – 3) = 12 degrees of freedom for the desired level of ( =. 05 used here): Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 32

The Tukey-Kramer Procedure: Example (continued) 3. Compute Critical Range: 4. Compare: 5. All of the absolute mean differences are greater than critical range. Therefore there is a significant difference between each pair of means at 5% level of significance. Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 33

Tukey-Kramer in PHStatistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 34

Two-Way ANOVA n Examines the effect of n Two factors of interest on the dependent variable n n e. g. , Percent carbonation and line speed on soft drink bottling process Interaction between the different levels of these two factors n e. g. , Does the effect of one particular carbonation level depend on which level the line speed is set? Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 35

Two-Way ANOVA (continued) n Assumptions n Populations are normally distributed n Populations have equal variances n Independent random samples are drawn Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 36

Two-Way ANOVA Sources of Variation Two Factors of interest: A and B r = number of levels of factor A c = number of levels of factor B n’ = number of replications for each cell n = total number of observations in all cells (n = rcn’) Xijk = value of the kth observation of level i of factor A and level j of factor B Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 37

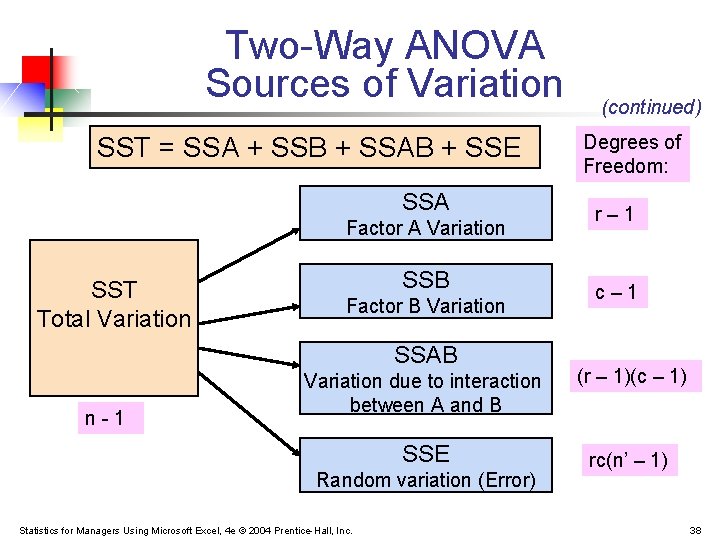
Two-Way ANOVA Sources of Variation SST = SSA + SSB + SSAB + SSE SSA Factor A Variation SST Total Variation SSB Factor B Variation SSAB n-1 (continued) Degrees of Freedom: r– 1 c– 1 Variation due to interaction between A and B (r – 1)(c – 1) SSE rc(n’ – 1) Random variation (Error) Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 38

Two Factor ANOVA Equations Total Variation: Factor A Variation: Factor B Variation: Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 39

Two Factor ANOVA Equations (continued) Interaction Variation: Sum of Squares Error: Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 40

Two Factor ANOVA Equations (continued) where: r = number of levels of factor A c = number of levels of factor B n’ = number of replications in each cell Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 41

Mean Square Calculations Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 42

Two-Way ANOVA: The F Test Statistic H 0: μ 1. . = μ 2. . = μ 3. . = • • • H 1: Not all μi. . are equal H 0: μ. 1. = μ. 2. = μ. 3. = • • • H 1: Not all μ. j. are equal H 0: the interaction of A and B is equal to zero H 1: interaction of A and B is not zero Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. F Test for Factor A Effect Reject H 0 if F > FU F Test for Factor B Effect Reject H 0 if F > FU F Test for Interaction Effect Reject H 0 if F > FU 43

Two-Way ANOVA Summary Table Source of Variation Sum of Squares Degrees of Freedom Factor A SSA r– 1 Factor B SSB c– 1 AB (Interaction) SSAB (r – 1)(c – 1) Error SSE rc(n’ – 1) Total SST n– 1 Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. Mean Squares F Statistic MSA MSE = SSA /(r – 1) MSB = SSB /(c – 1) MSAB = SSAB / (r – 1)(c – 1) MSB MSE MSAB MSE = SSE/rc(n’ – 1) 44

Features of Two-Way ANOVA F Test n n n Degrees of freedom always add up n n-1 = rc(n’-1) + (r-1) + (c-1) + (r-1)(c-1) n Total = error + factor A + factor B + interaction The denominator of the F Test is always the same but the numerator is different The sums of squares always add up n SST = SSE + SSA + SSB + SSAB n Total = error + factor A + factor B + interaction Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 45

Examples: Interaction vs. No Interaction No interaction: Interaction is present: Factor B Level 3 Factor B Level 2 Factor A Levels Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. Mean Response Factor B Level 1 Mean Response n n Factor B Level 1 Factor B Level 2 Factor B Level 3 Factor A Levels 46

Chapter Summary n n Described one-way analysis of variance n The logic of ANOVA n ANOVA assumptions n F test for difference in c means n The Tukey-Kramer procedure for multiple comparisons Described two-way analysis of variance n Examined effects of multiple factors n Examined interaction between factors Statistics for Managers Using Microsoft Excel, 4 e © 2004 Prentice-Hall, Inc. 47