Statistics for biological data Significance tests for continuous

Statistics for biological data Significance tests for continuous variables Aya Elwazir Teaching assistant of medical genetics, FOMSCU Ph. D student, University of Sheffield

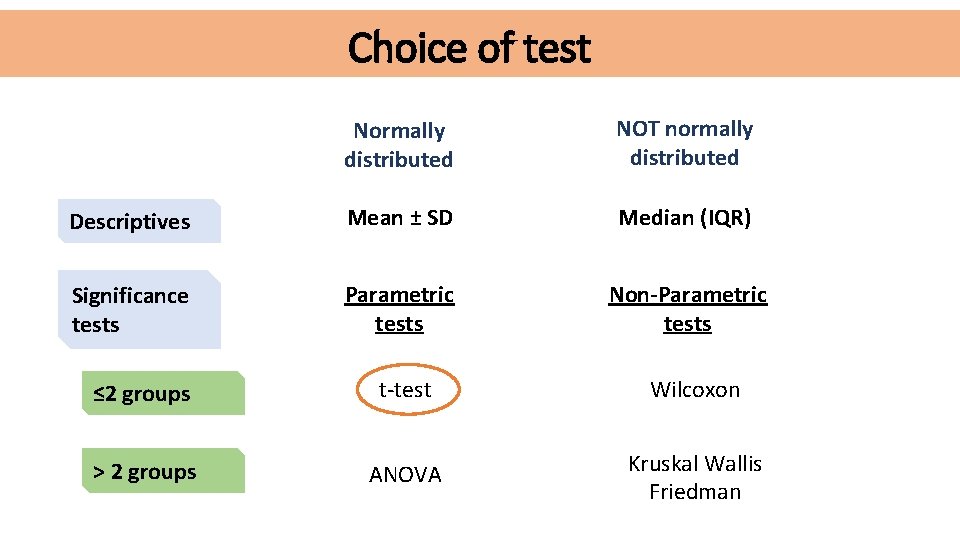
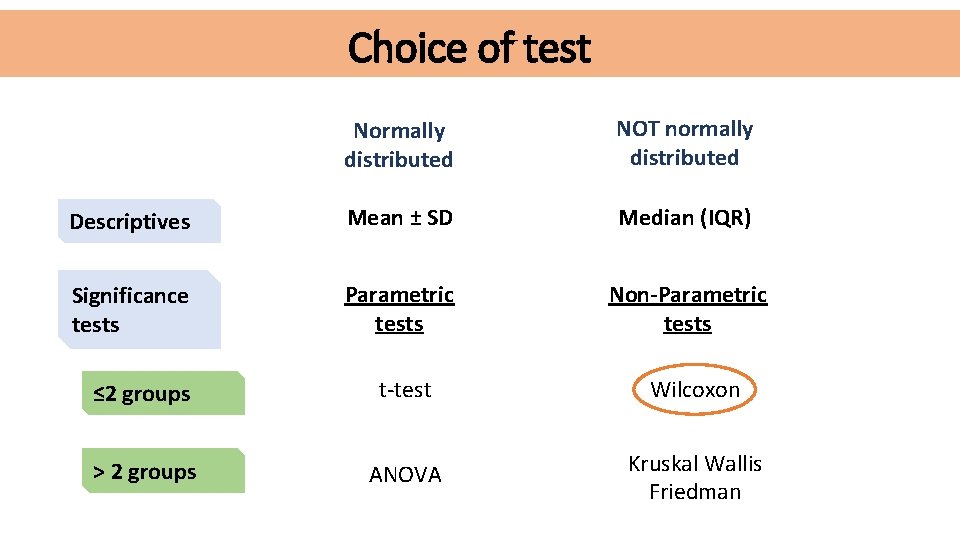
Choice of test Normally distributed NOT normally distributed Descriptives Mean ± SD Median (IQR) Significance tests Parametric tests Non-Parametric tests ≤ 2 groups t-test Wilcoxon > 2 groups ANOVA Kruskal Wallis Friedman

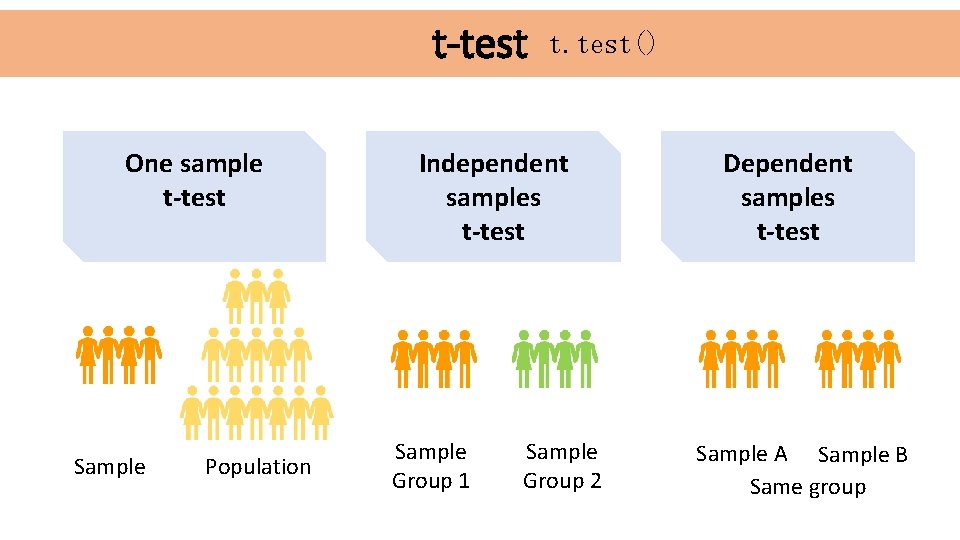
t-test One sample t-test Sample Population t. test() Independent samples t-test Sample Group 1 Sample Group 2 Dependent samples t-test Sample A Sample B Same group

One sample t-test Compare the mean of the sample [x ] with a pre-specified value (population mean [µ]) Average score of medical students in UK universities = 72 We think that the average score of medical students in the University of Sheffield is higher H 0 x ≤ µ H 1 x > µ x ≤ 72 x > 72 t. test(num. Var, mu=) t. test(Score, mu=72) Numeric Student name Score John 63. 5 Sue 71. 2 Sarah 56. 6 Nick 80. 0 Ben 79. 4

Independent sample t-test Compare the mean between 2 independent groups [x 1 , x 2] Average score of medical students between University of Sheffield & University of Leeds H 0 x 1 = x 2 H 1 x 1 ≠ x 2 t. test(num. Var ~ categ. Var) t. test(Score University) ~ Categorical (grouping) Numeric Student name University Score John Sheffield 63. 5 Marwa Sheffield 71. 3 Sarah Sheffield 56. 5 Nick Sheffield 80. 0 Ben Sheffield 79. 3 Ruby Leeds 83. 3 Ahmed Leeds 73. 5 Beth Leeds 55. 0 Sue Leeds 67. 0 Claire Leeds 46. 5

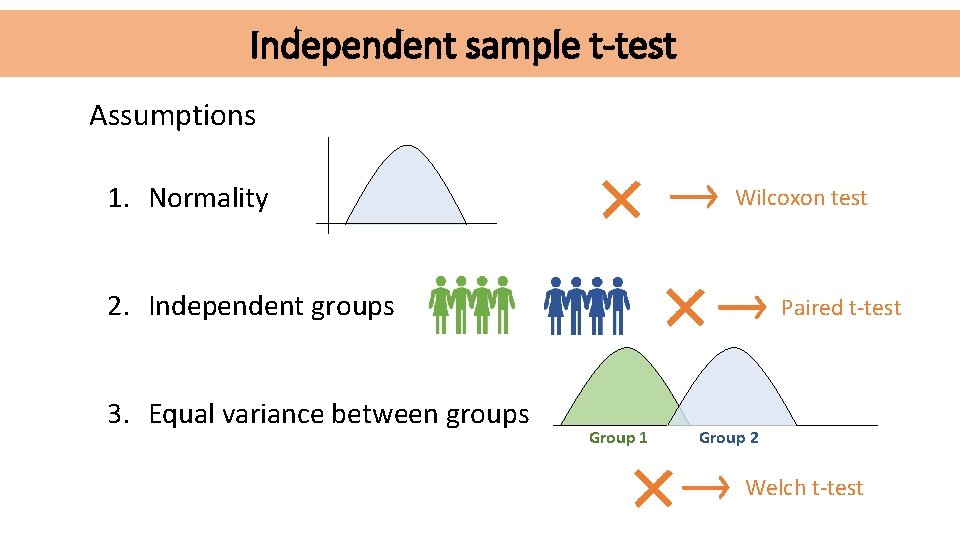
Independent sample t-test Assumptions 1. Normality Wilcoxon test 2. Independent groups 3. Equal variance between groups Paired t-test Group 1 Group 2 Welch t-test

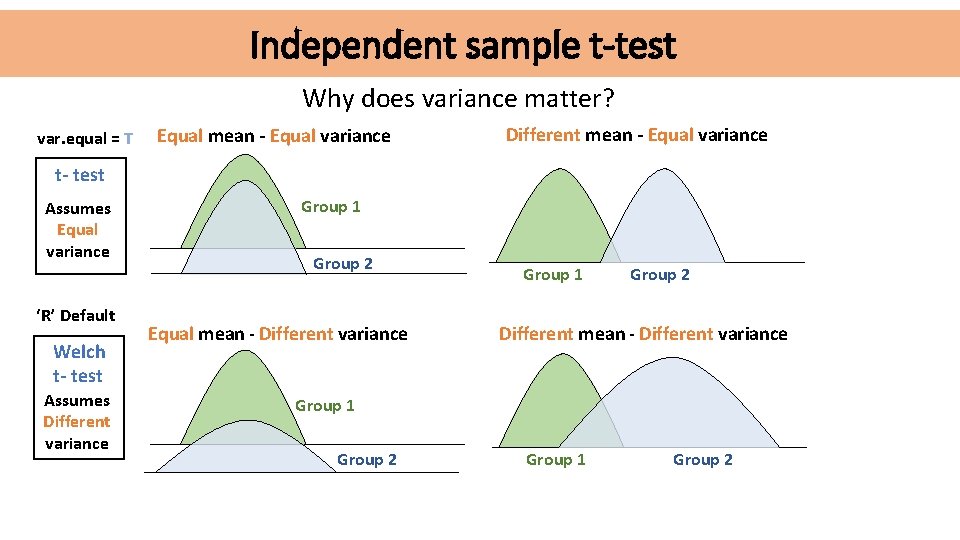
Independent sample t-test Why does variance matter? var. equal = T Equal mean - Equal variance Different mean - Equal variance t- test Assumes Equal variance ‘R’ Default Welch t- test Assumes Different variance Group 1 Group 2 Equal mean - Different variance Group 1 Group 2 Different mean - Different variance Group 1 Group 2

Dependent sample t-test Also called paired t-test Numeric Compare the mean between 2 dependent groups [x , x ’] Average score of medical students at University of Sheffield before & after a ‘course revision’ module H 0 x = x ‘ H 1 x ≠ x ‘ Student Pre name Post John 63. 5 65. 5 Sue 71. 2 80. 3 Sarah 56. 6 52. 5 Nick 80. 0 80. 5 Ben 79. 4 86. 3 t. test(num. Var 1 , num. Var 2 , paired=T) t. test( , paired=T) Pre , Post

Choice of test Normally distributed NOT normally distributed Descriptives Mean ± SD Median (IQR) Significance tests Parametric tests Non-Parametric tests ≤ 2 groups t-test Wilcoxon > 2 groups ANOVA Kruskal Wallis Friedman

Wilcoxon-test wilcox. test(num. Var, mu=) One-Sample Wilcoxon Signed Rank Test Sample Population wilcox. test() wilcox. test(num. Var 1~categ. Var) wilcox. test(num. Var 1, num. Var 2, paired=T) Wilcoxon– Mann–Whitney test Sample Group 1 Sample Group 2 Wilcoxon Signed. Rank Test Sample A Sample B Same group

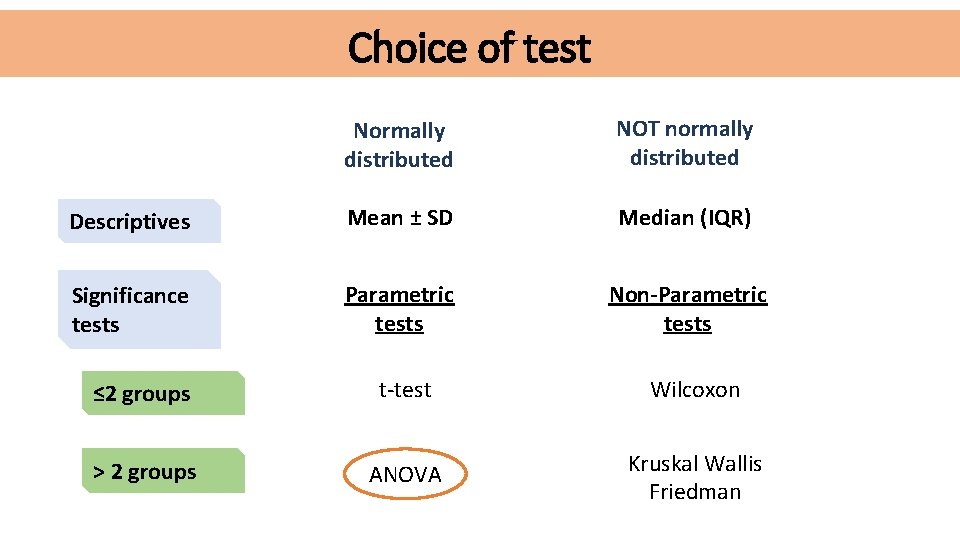
Choice of test Normally distributed NOT normally distributed Descriptives Mean ± SD Median (IQR) Significance tests Parametric tests Non-Parametric tests ≤ 2 groups t-test Wilcoxon > 2 groups ANOVA Kruskal Wallis Friedman

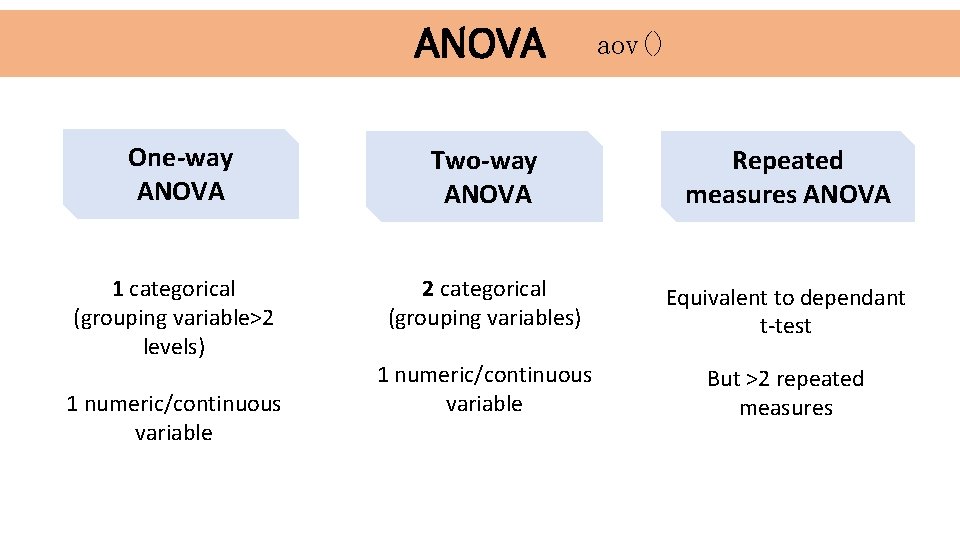
ANOVA aov() One-way ANOVA Two-way ANOVA Repeated measures ANOVA 1 categorical (grouping variable>2 levels) 2 categorical (grouping variables) Equivalent to dependant t-test 1 numeric/continuous variable But >2 repeated measures 1 numeric/continuous variable

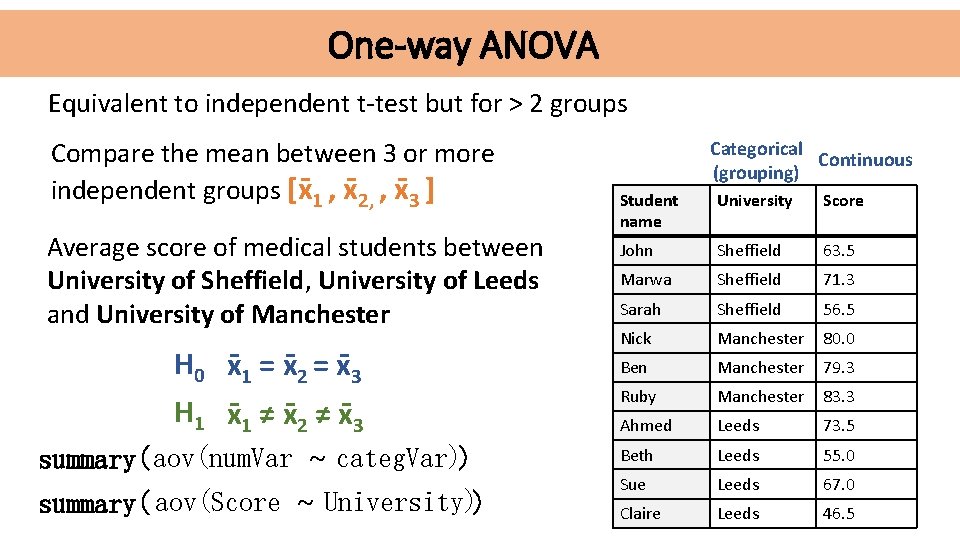
One-way ANOVA Equivalent to independent t-test but for > 2 groups Compare the mean between 3 or more independent groups [x 1 , x 2, , x 3 ] Average score of medical students between University of Sheffield, University of Leeds and University of Manchester H 0 x 1 = x 2 = x 3 H 1 x 1 ≠ x 2 ≠ x 3 summary( aov(num. Var ~ categ. Var)) summary( aov(Score ~ University)) Categorical Continuous (grouping) Student name University Score John Sheffield 63. 5 Marwa Sheffield 71. 3 Sarah Sheffield 56. 5 Nick Manchester 80. 0 Ben Manchester 79. 3 Ruby Manchester 83. 3 Ahmed Leeds 73. 5 Beth Leeds 55. 0 Sue Leeds 67. 0 Claire Leeds 46. 5

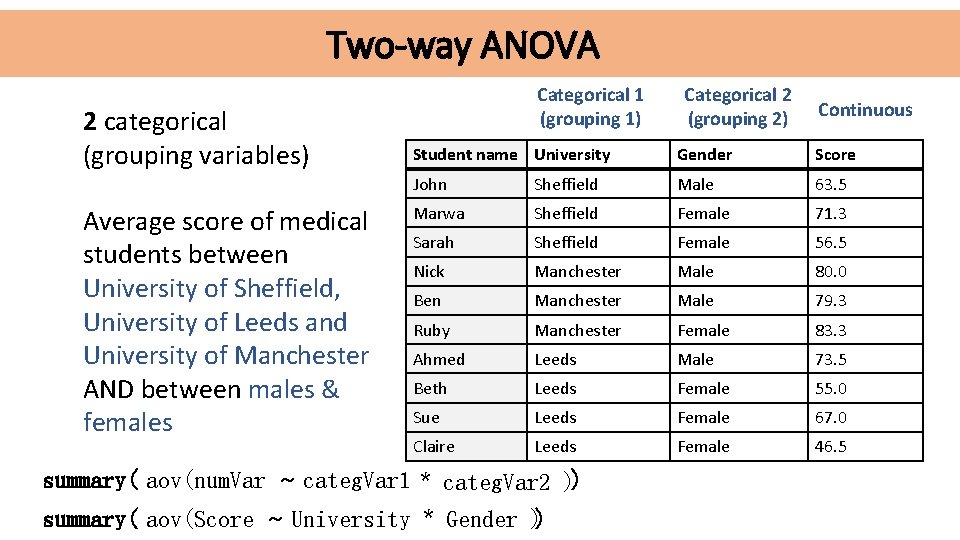
Two-way ANOVA 2 categorical (grouping variables) Average score of medical students between University of Sheffield, University of Leeds and University of Manchester AND between males & females Categorical 1 (grouping 1) Categorical 2 (grouping 2) Continuous Student name University Gender Score John Sheffield Male 63. 5 Marwa Sheffield Female 71. 3 Sarah Sheffield Female 56. 5 Nick Manchester Male 80. 0 Ben Manchester Male 79. 3 Ruby Manchester Female 83. 3 Ahmed Leeds Male 73. 5 Beth Leeds Female 55. 0 Sue Leeds Female 67. 0 Claire Leeds Female 46. 5 summary( aov(num. Var ~ categ. Var 1 * categ. Var 2 )) summary( aov(Score ~ University * Gender ))

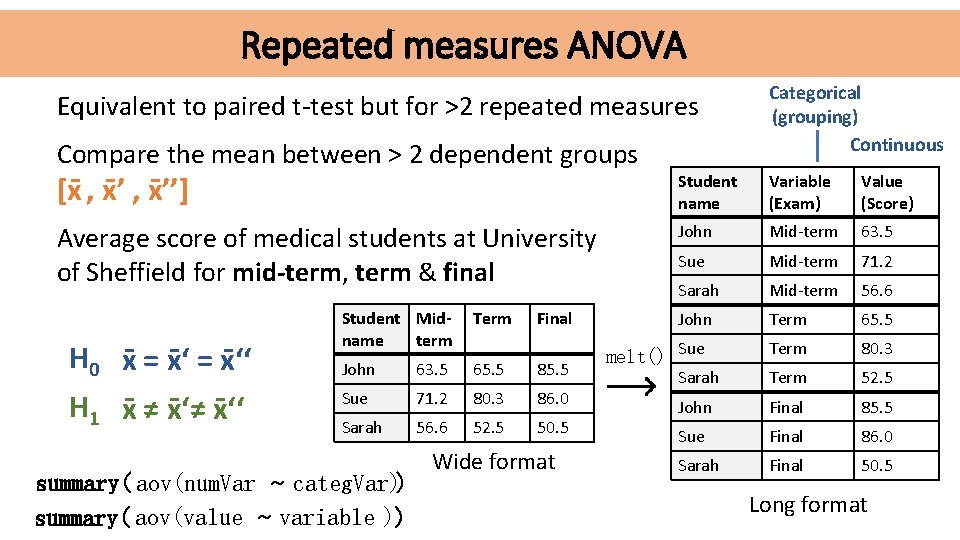
Repeated measures ANOVA Equivalent to paired t-test but for >2 repeated measures Compare the mean between > 2 dependent groups Categorical (grouping) Continuous [x , x ’’] Student name Variable (Exam) Value (Score) Average score of medical students at University of Sheffield for mid-term, term & final John Mid-term 63. 5 Sue Mid-term 71. 2 Sarah Mid-term 56. 6 John Term 65. 5 Term 80. 3 Sarah Term 52. 5 John Final 85. 5 Sue Final 86. 0 Sarah Final 50. 5 H 0 x = x ‘‘ H 1 x ≠ x ‘‘ Student Midname term Term John 63. 5 65. 5 85. 5 Sue 71. 2 80. 3 86. 0 Sarah 56. 6 52. 5 50. 5 summary( aov(num. Var ~ categ. Var)) summary( aov(value ~ variable )) Final Wide format melt() Sue Long format

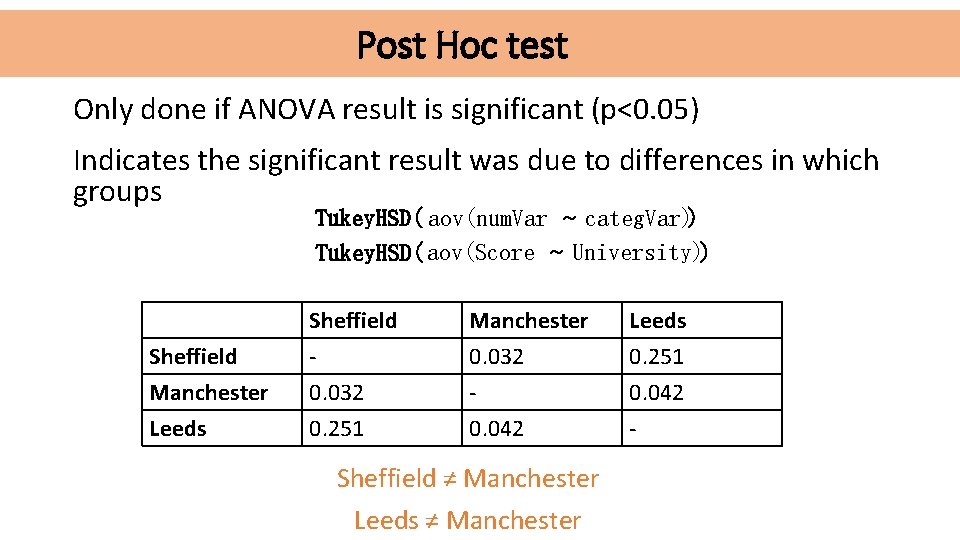
Post Hoc test Only done if ANOVA result is significant (p<0. 05) Indicates the significant result was due to differences in which groups Tukey. HSD( aov(num. Var ~ categ. Var)) Tukey. HSD( aov(Score ~ University)) Sheffield Manchester Leeds Sheffield 0. 032 0. 251 Manchester 0. 032 0. 042 Sheffield ≠ Manchester Leeds 0. 251 0. 042 -

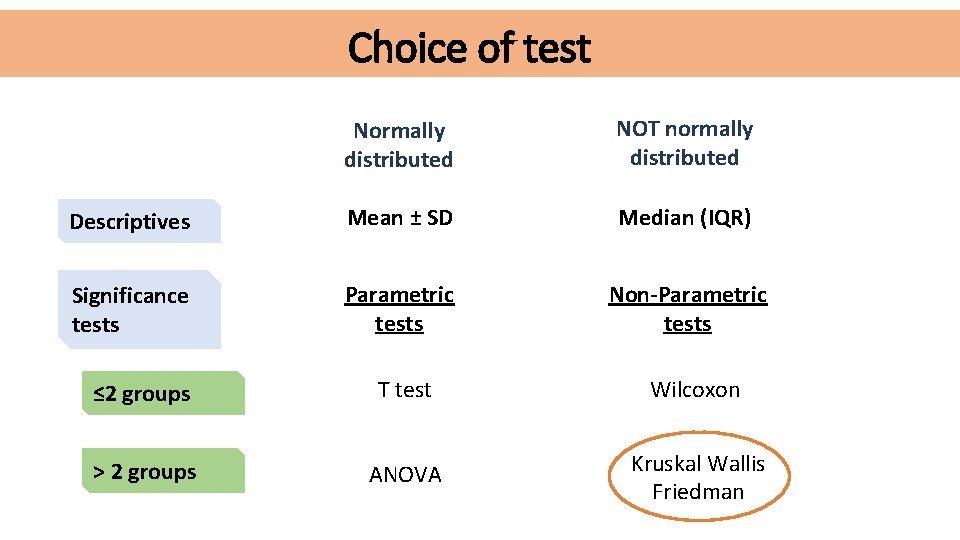
Choice of test Normally distributed NOT normally distributed Descriptives Mean ± SD Median (IQR) Significance tests Parametric tests Non-Parametric tests ≤ 2 groups T test Wilcoxon > 2 groups ANOVA Kruskal Wallis Friedman

Kruskal Wallis - Friedman Kruskal Wallis test Friedman test Equivalent to one-way ANOVA Equivalent to repeated measures ANOVA for non-parametric data kruskal. test(num. Var ~ categ. Var) friedman. test(as. matrix(dataframe of num. Vars))

Statistics for biological data Introduction to statistics Course Objectives 1. Contingency tables & testing for categorial variables 2. Normality testing & Descriptive statistics 3. Testing for continuous variables Lots of practice!