STATISTICS Exploratory Data Analysis Professor KeSheng Cheng Department

STATISTICS Exploratory Data Analysis Professor Ke-Sheng Cheng Department of Bioenvironmental Systems Engineering/Master Program in Statistics National Taiwan University 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 1

What is “statistics”? • Statistics is a science of “reasoning” from data. • A body of principles and methods for extracting useful information from data, for assessing the reliability of that information, for measuring and managing risk, and for making decisions in the face of uncertainty. • Statistics vs data science • https: //www. displayr. com/statistics-vs-data-science-whatsthedifference/#: ~: text=Statistics%20 is%20 a%20 mathematicall y%2 Dbased, in%20 a%20 range%20 of%20 forms. 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 2

• The major difference between statistics and mathematics is that statistics always needs “observed” data, while mathematics does not. • An important feature of statistical methods is the “uncertainty” involved in analysis. A population is defined as the set of all measurements or objects that are of interest. A sample is a subset of data selected from a population. The size of a sample is the number of elements in it. 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 3

• Statistics is the discipline concerned with the study of variability, with the study of uncertainty and with the study of decision-making in the face of uncertainty. As these are issues that are crucial throughout the sciences and engineering, statistics is an inherently interdisciplinary science. 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 4

Stochastic Modeling & Simulation • Building probability models for real world phenomena. • No matter how sophisticated a model is, it only represents our understanding of the complicated natural systems. • Generating a large number of possible realizations. • Making decisions or assessing risks based on simulation results. • Conducted by computers. 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 5

What is EDA? • Exploratory Data Analysis refers to the critical process of performing initial investigations on data so as to discover patterns, to spot anomalies, to test hypothesis and to check assumptions with the help of summary statistics and graphical representations. 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 6

Exploratory Data Analysis • Features of data distributions • Histograms • Center: mean, median • Spread: variance, standard deviation, range • Shape: skewness, kurtosis • Order statistics and sample quantiles • Clusters • Extreme observations: outliers 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 7

• Histogram: frequencies and relative frequencies • A sample data set X 104. 838935 22. 371870 24. 762863 82. 708815 82. 535199 115. 387515 64. 158533 72. 895810 85. 553281 102. 347372 12/22/2021 265. 018615 129. 538575 275. 440477 149. 905426 150. 761192 102. 460651 133. 663194 107. 569047 96. 920012 19. 277535 205. 279506 37. 587841 70. 721022 113. 442704 134. 931864 16. 480639 139. 201204 81. 266071 34. 202372 134. 484317 146. 938446 12. 577133 231. 608794 60. 397366 100. 717110 33. 918756 131. 144892 9. 539663 174. 200632 130. 360126 9. 961515 53. 449806 112. 180103 105. 368124 101. 351639 16. 652365 45. 472935 149. 996985 121. 101643 10. 382787 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 8

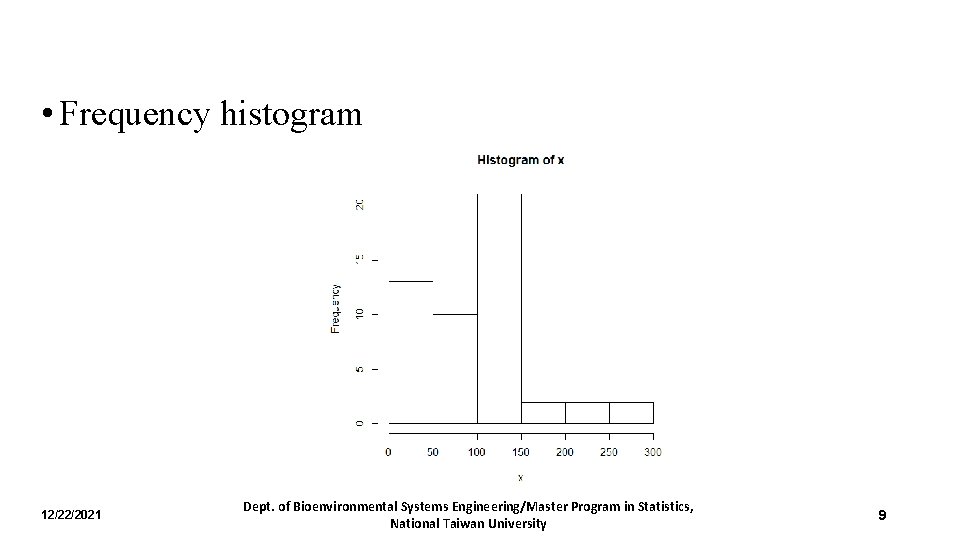
• Frequency histogram 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 9

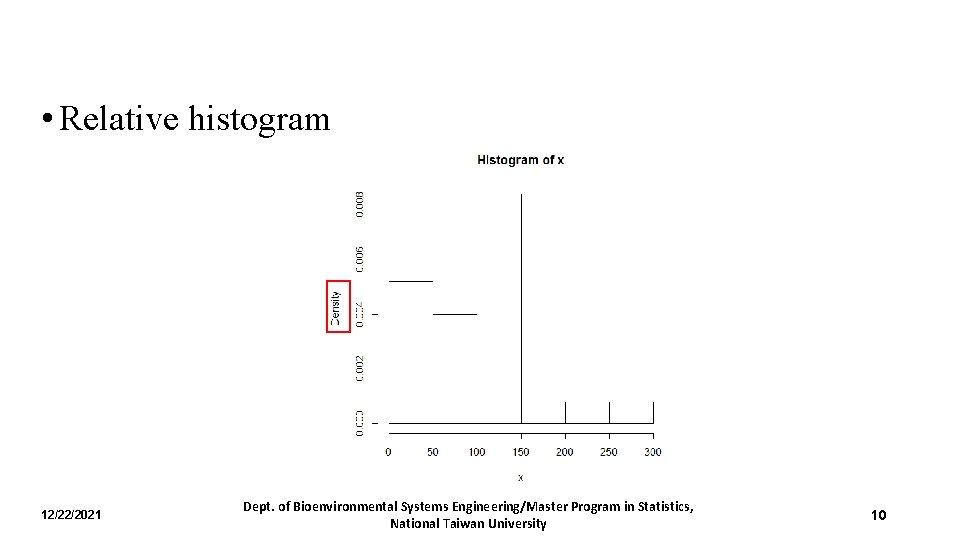
• Relative histogram 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 10

• Measures of center • Sample mean • Sample median（樣本中位數） 12/22/2021 Sample mean = 98. 26067 Sample median = 101. 8495 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 11

• One desirable property of the sample median is that it is resistant to extreme observations, in the sense that its value depends only the values of the middle observations, and is quite unaffected by the actual values of the outer observations in the ordered list. The same cannot be said for the sample mean. Any significant changes in the magnitude of an observation results in a corresponding change in the value of the mean. Hence, the sample mean is said to be sensitive to extreme observations. 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 12

• Measures of spread • Sample variance and sample standard deviation （樣本變異數，樣本變方） （樣本標準差） • Range • the difference between the largest and smallest values Sample variance = 4039. 931 Sample standard deviation = 63. 56045 Range = 265. 9008 (275. 440477 – 9. 539663) 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 13

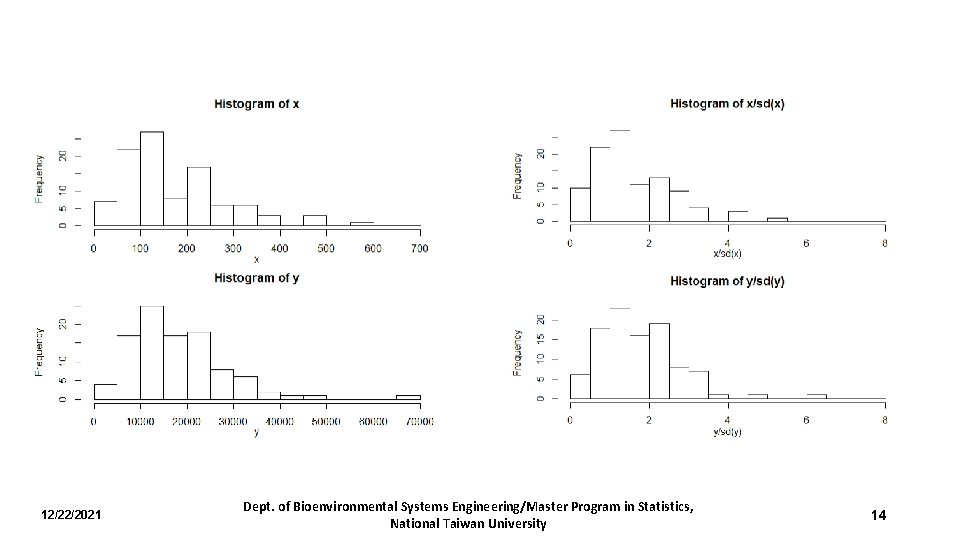
12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 14

• Measures of shape • Sample skewness （樣本偏度） • Sample kurtosis （樣本峰度） Sample skewness = 0. 7110874 Sample kurtosis = 0. 533141 (or 3. 533141 in R) You need to install the moments package in R in order to calculate the sample skewness and kurtosis. 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 15

• Order statistics （順序統計量） • Sample quantiles（樣本分位數） Linear interpolation 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 16

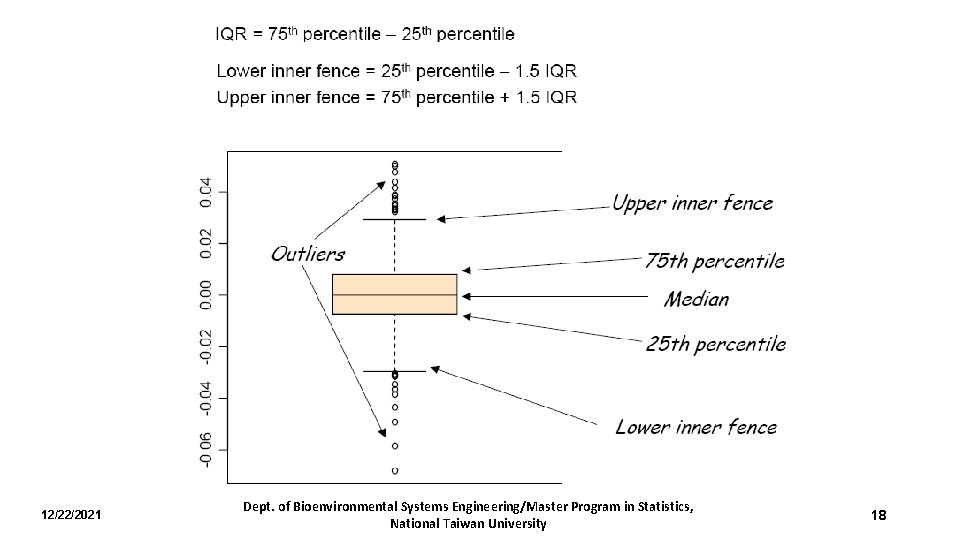
• Box-and-whisker plot (or boxplot) • A box-and-whisker plot includes two major parts – the box and the whiskers. • A parameter range determines how far the plot whiskers extend out from the box. If range is positive, the whiskers extend to the most extreme data point which is no more than range times the interquartile range (IQR) from the box. A value of zero causes the whiskers to extend to the data extremes. • Outliers are marked by points which fall beyond the whiskers. • Hinges and the five-number summary 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 17

12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 18

Not “linear interpolation” • In R, a boxplot is essentially a graphical representation determined by the 5 NS. The summary function in R yields a list of six numbers: 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 19

Determining the lower and upper hinges • The lower hinge is the median of the lower half of the data, and the upper hinge the median of the upper half of the data. • When the number of data points, say n, is even, there are (n/2) data points in the lower and upper halves. • When n is odd, there are (n+1)/2 data points in the lower and upper halves. The median is considered as a data point in both the lower and upper halves. 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 20

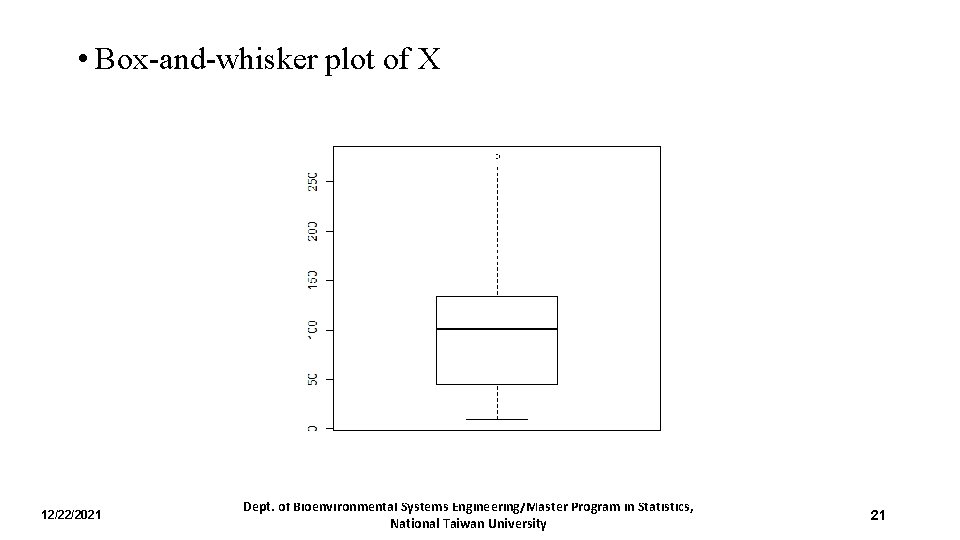
• Box-and-whisker plot of X 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 21

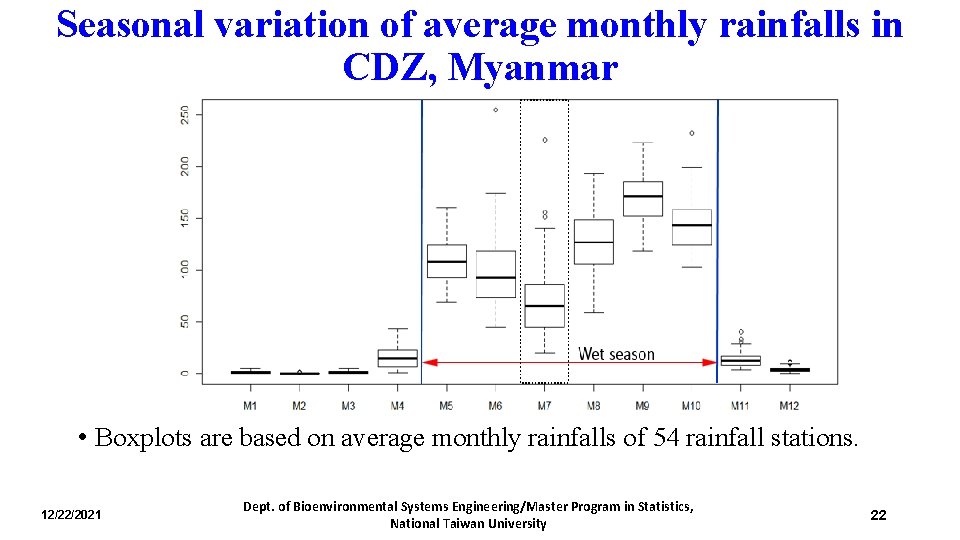
Seasonal variation of average monthly rainfalls in CDZ, Myanmar • Boxplots are based on average monthly rainfalls of 54 rainfall stations. 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 22

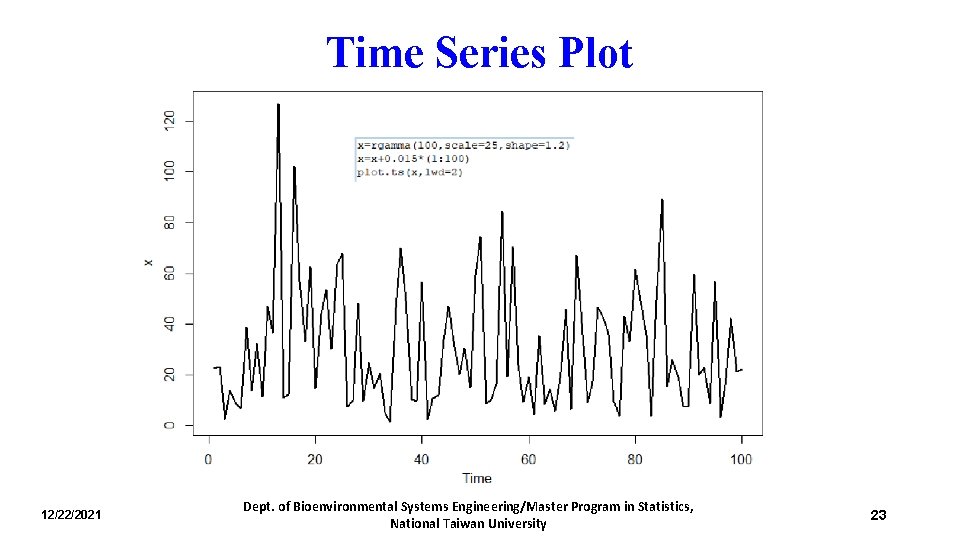
Time Series Plot 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 23

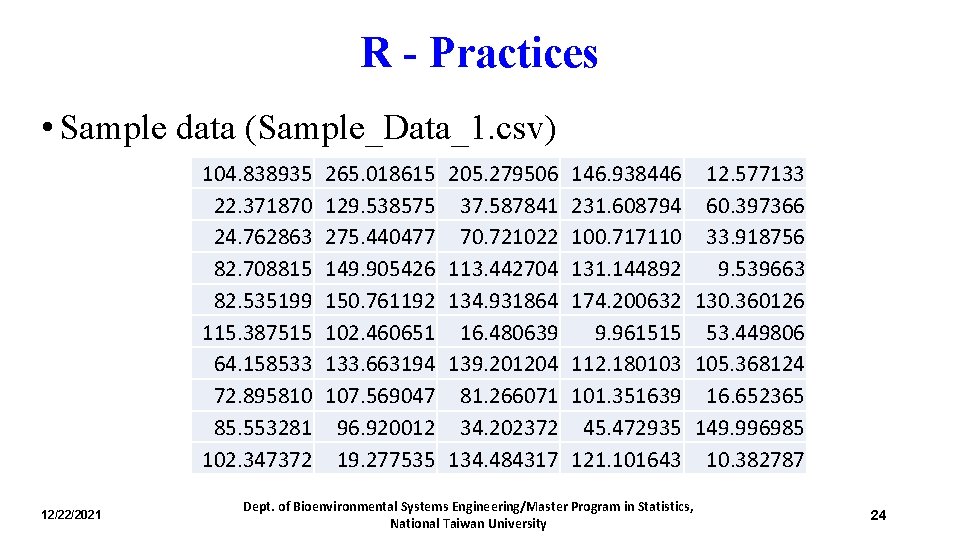
R - Practices • Sample data (Sample_Data_1. csv) 104. 838935 22. 371870 24. 762863 82. 708815 82. 535199 115. 387515 64. 158533 72. 895810 85. 553281 102. 347372 12/22/2021 265. 018615 129. 538575 275. 440477 149. 905426 150. 761192 102. 460651 133. 663194 107. 569047 96. 920012 19. 277535 205. 279506 37. 587841 70. 721022 113. 442704 134. 931864 16. 480639 139. 201204 81. 266071 34. 202372 134. 484317 146. 938446 12. 577133 231. 608794 60. 397366 100. 717110 33. 918756 131. 144892 9. 539663 174. 200632 130. 360126 9. 961515 53. 449806 112. 180103 105. 368124 101. 351639 16. 652365 45. 472935 149. 996985 121. 101643 10. 382787 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 24

x=scan("Sample_Data_1. csv", sep=", ") mode(x); class(x); length(x) x # --------------------x 1=read. table("Sample_Data_1. csv", sep=", ", header=FALSE) mode(x 1); class(x 1); length(x 1) x 1[6, 3] x 1[26] # -------------------x 2=matrix(x, ncol=5) mode(x 2); class(x 2); length(x 2) x 2[6, 3] x 2[26] # --------------------x 3=t(matrix(x, nrow=5)) mode(x 3); class(x 3); length(x 3) x 3[6, 3] x 3[26] # --------------------x 1[[3]][6] # select sub-objects from a list x 1[[3]][3: 8] x 1[3]; length(x 1[3]) x 1[[3]]; length(x 1[[3]]) 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 25

zzz=list(x 1, x 3) mode(zzz); class(zzz); length(zzz) mode(zzz[1]); class(zzz[1]); length(zzz[1]) mode(zzz[[1]]); class(zzz[[1]]); length(zzz[[1]]) mode(zzz[[1]][1]); class(zzz[[1]][1]); length(zzz[[1]][1]) zzz[[1]][1] mode(zzz[[1]]); class(zzz[[1]]); length(zzz[[1]]) zzz[[1]] # mode(zzz[2]); class(zzz[2]); length(zzz[2]) mode(zzz[[2]]); class(zzz[[2]]); length(zzz[[2]]) mode(zzz[[2]][1]); class(zzz[[2]][1]); length(zzz[[2]][1]) zzz[[2]][1] 12/22/2021 Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 26

Matrices, Data Frame, and List • Matrices • Mode: numerical • Class: matrix • Data frame • Mode: list • Class: data frame • List • Mode: list • Class: list or data frame 12/22/2021 A matrix is a set of numerical values arranged in matrix format. A matrix is a vector with a dimension vector. A data frame is a particular kind of list. A data frame is a collection of vectors of equal length. These vectors can be numerical, logical, or characters. Although a data frame is a list, its elements can be accessed in a way similar to a matrix. Dept. of Bioenvironmental Systems Engineering/Master Program in Statistics, National Taiwan University 27