Statistics Counting Two Specific Models 1 Binomial Distribution
Statistics & Counting

Two Specific Models: 1. Binomial Distribution – generally applicable to all constant-p processes. Cumbersome for large samples (large factorial numbers) 2. Poisson Distribution – simplification to the Binomial Distribution if the success probability “p” is small.

The Binomial Distribution n = number of trials p = probability of success for each trial We can then predict the probability of counting exactly “x” successes: P(x) is the predicted “Probability Distribution Function”

Example of the Binomial Distribution “Winners”: 3, 4, 5, or 6 P = 4/6 or 2/3 10 rolls of the die: n=10
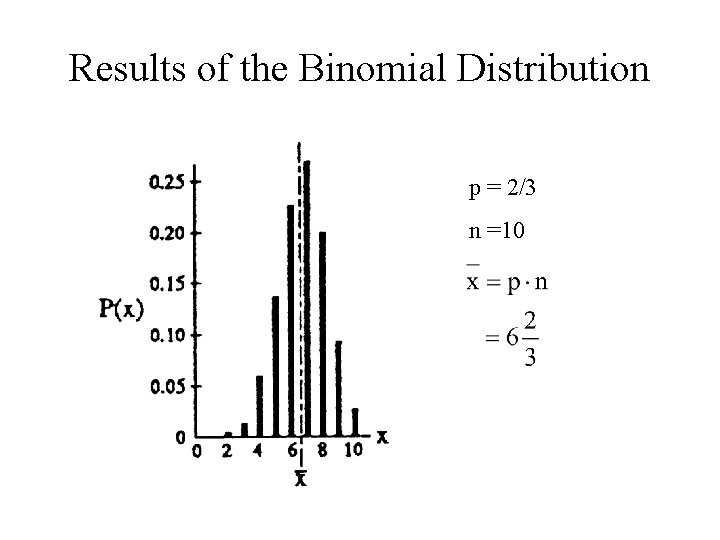
Results of the Binomial Distribution p = 2/3 n =10

Some Properties of the Binomial Distribution It is normalized: Mean (average) value

Standard Deviation “Predicted variance” “Standard Deviation” s is a “typical” value for

For the Binomial Distribution: where n = number of trials and p = success probability Predicted Variance: Standard Deviation:

For our Previous Example p = 2/3 n = 10

The Poisson Distribution Provided p << 1

For the Poisson Distribution Predicted Mean: Predicted Variance: Standard Deviation:

Example of the Application of Poisson Statistics “Is your birthday today? ” Example: what is the probability that 4 people out of 1000 have a birthday today?

Discrete Poisson Distribution

Other examples of Poisson • • The number of traffic accidents in a city. The number of calls you received in a day. Type errors on a page. Number of alpha particles emitted by a radioactive substance in a given time.

Average and Standard deviation • If we measure a quantity X N times, the best estimate for the value of that quantity is the average: • The spread in the measurements is given by the standard deviation:

The “Error Propagation Formula” Given: directly measured counts (or other independent variables) x, y, z, … for which the associated standard deviations are known to be sx , sy , sz , … Derive: the standard deviation of any calculated quantity u(x, y, z, …)

Sums or Differences of Counts u=x+y Recall: or u = x - y

Example of Difference of Counts total = x = 2612 background = y = 1295 net = u = 1317 Therefore, net counts = 1317 ± 62. 5

Multiplication or Division by a Constant

Example of Division by a Constant Calculation of a counting rate x = 11, 367 counts t = 300 s rate r = 37. 89 ± 0. 36 s-1

Multiplication or Division of Counts
- Slides: 21