Statistics 101 Chapter 3 Section 3 Least Squares

Least – Squares Regression ¢ Method for finding a line that summarizes the relationship

Regression Line A straight line that describes how a response variable y changes as

Calculating error Error = observed – predicted ¢ = 5. 1 – 4. 9

Least – squares regression line (LSRL) ¢ Line that makes the sum of the

¢ http: //hadm. sph. sc. edu/courses/J 716/ demos/leastsquaresdem o. html

What we need y = a + bx ¢ b = r (sy/ sx)

Statistics 101 Chapter 3 Section 3 Part 2

Facts about least-squares regression Fact 1: the distinction between explanatory and response variables is

More facts Fact 3: The least-squares regression line always passes through the point (x,

Residuals ¢ Is the difference between an observed value of the response variable and

Residuals If the residual is positive it lies above the line ¢ If the

Residual plots A scatterplot of the regression residuals against the explanatory variable. ¢ To

Curved pattern ¢ A curved pattern shows that the relationship is not linear.

Increasing or decreasing spread ¢ Indicates that prediction of y will be less accurate

Influential Observations ¢ An observation is an influential observation for a statistical calculation if

Slides: 28

Download presentation

Statistics 101 Chapter 3 Section 3

Least – Squares Regression ¢ Method for finding a line that summarizes the relationship between two variables

Regression Line A straight line that describes how a response variable y changes as an explanatory variable x changes. ¢ Mathematical model ¢

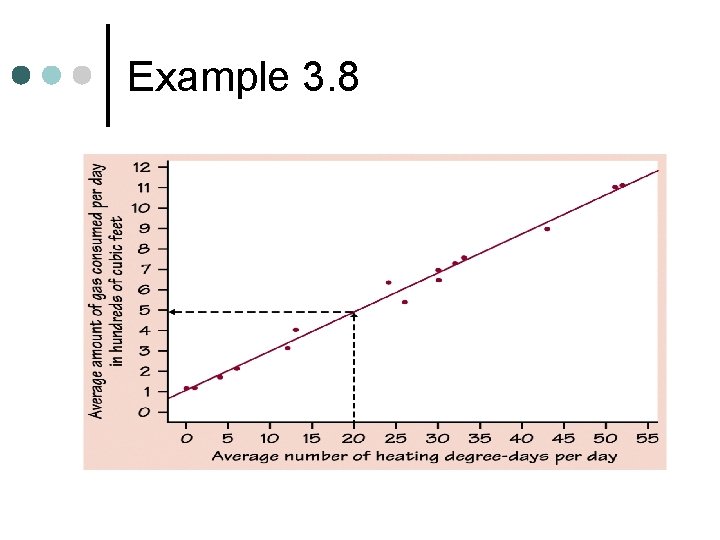
Example 3. 8

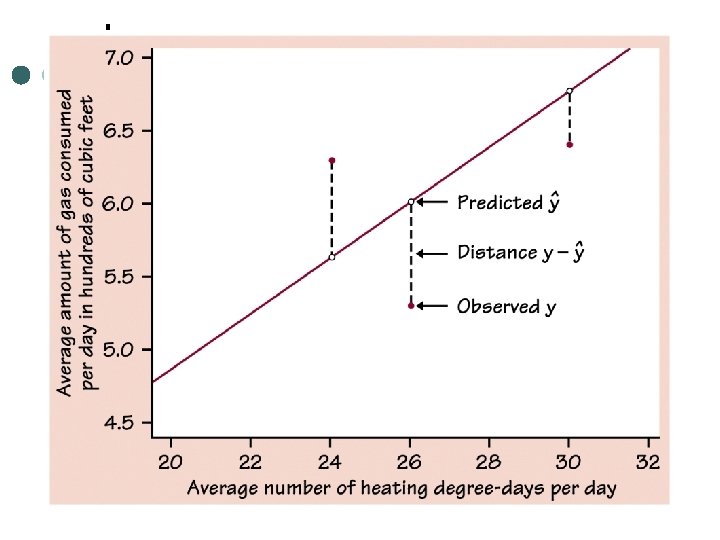
Calculating error Error = observed – predicted ¢ = 5. 1 – 4. 9 ¢ = 0. 2 ¢

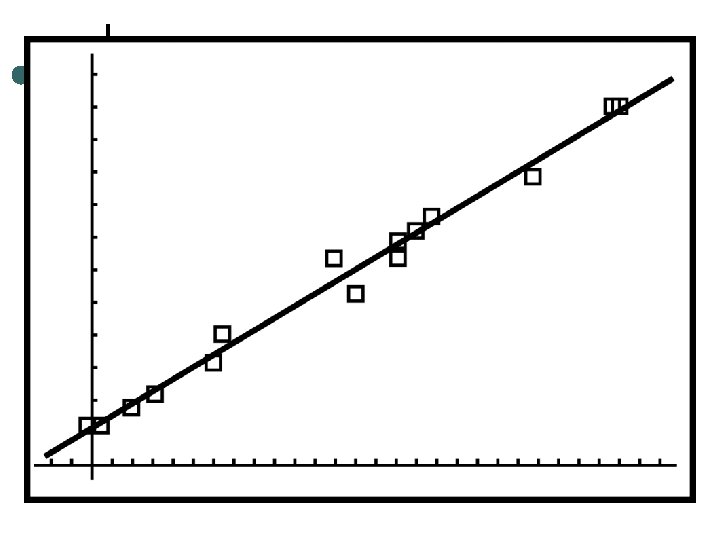
Least – squares regression line (LSRL) ¢ Line that makes the sum of the squares of the vertical distances of the data points from the line as small as possible

¢ http: //hadm. sph. sc. edu/courses/J 716/ demos/leastsquaresdem o. html

What we need y = a + bx ¢ b = r (sy/ sx) ¢ a = y - bx ¢

Try Example 3. 9

Technology toolbox pg. 154

Statistics 101 Chapter 3 Section 3 Part 2

Facts about least-squares regression Fact 1: the distinction between explanatory and response variables is essential ¢ Fact 2: There is a close connection between correlation and the slope ¢ l A change of one standard deviation in x corresponds to a change of r standard deviations in y

More facts Fact 3: The least-squares regression line always passes through the point (x, y) ¢ Fact 4: the square of the correlation, r 2, is the fraction of the variation in the values of y that is explained by the least-squares regression of y on x. ¢

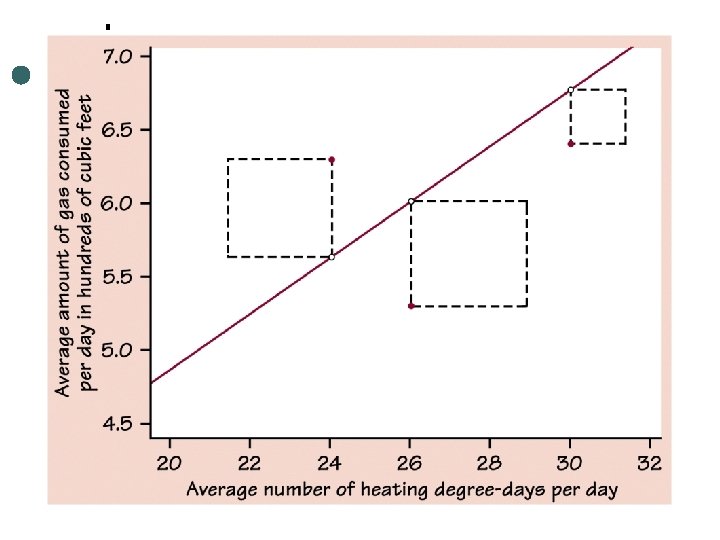
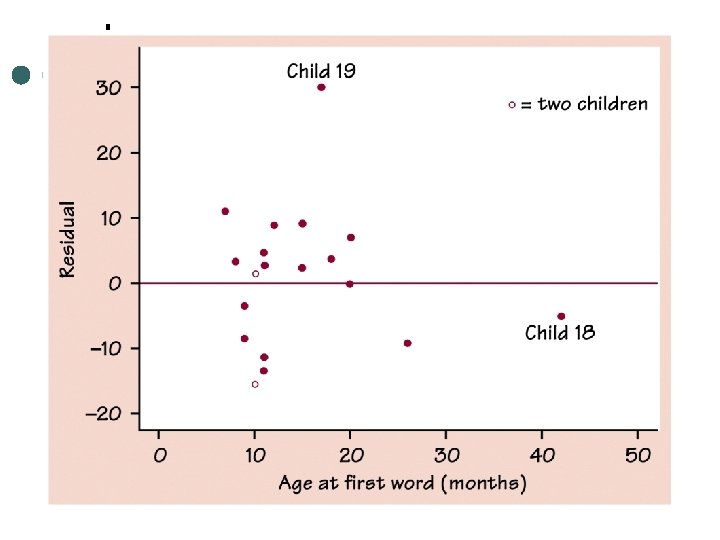
Residuals ¢ Is the difference between an observed value of the response variable and the value predicted by the regression line. • Residual = observed y – predicted y =y-y

Residuals If the residual is positive it lies above the line ¢ If the residual is negative it lies below the line ¢ The mean of the least-squares residuals is always zero ¢ If not then it is a roundoff error ¢ Technology Toolbox on page 174 shows how to do a residual plot. ¢

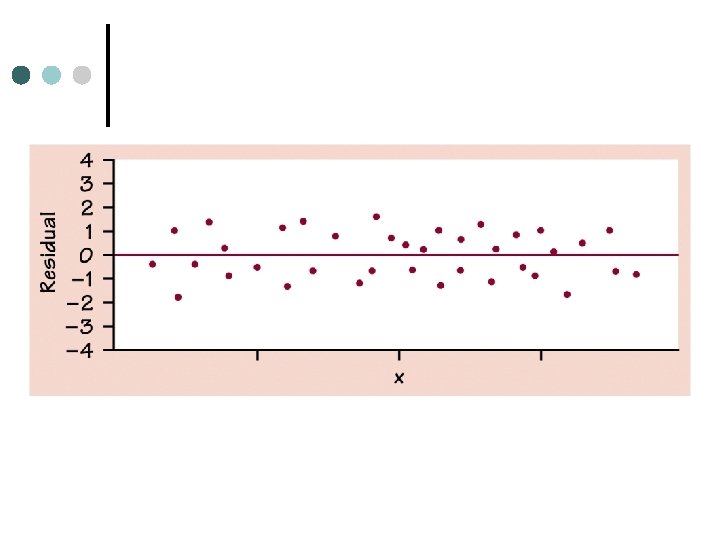
Residual plots A scatterplot of the regression residuals against the explanatory variable. ¢ To help us assess the fit of a regression line. ¢ If the regression line captures the overall relationship between x and y, the residuals should have no systemic pattern. ¢

Curved pattern ¢ A curved pattern shows that the relationship is not linear.

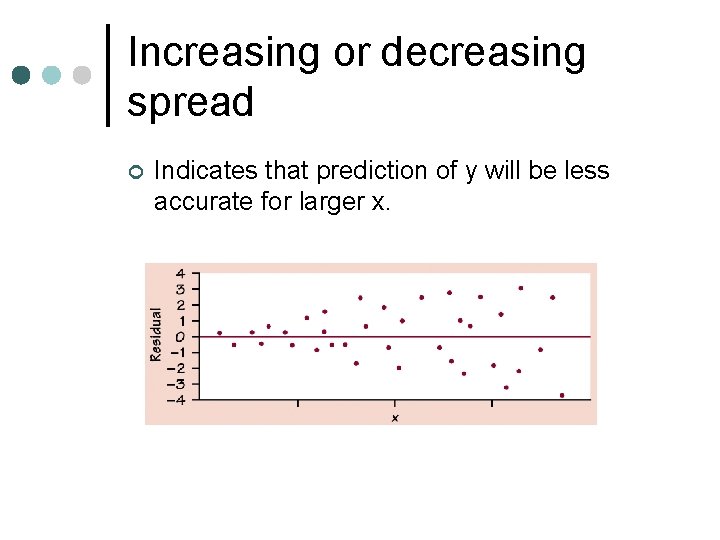
Increasing or decreasing spread ¢ Indicates that prediction of y will be less accurate for larger x.

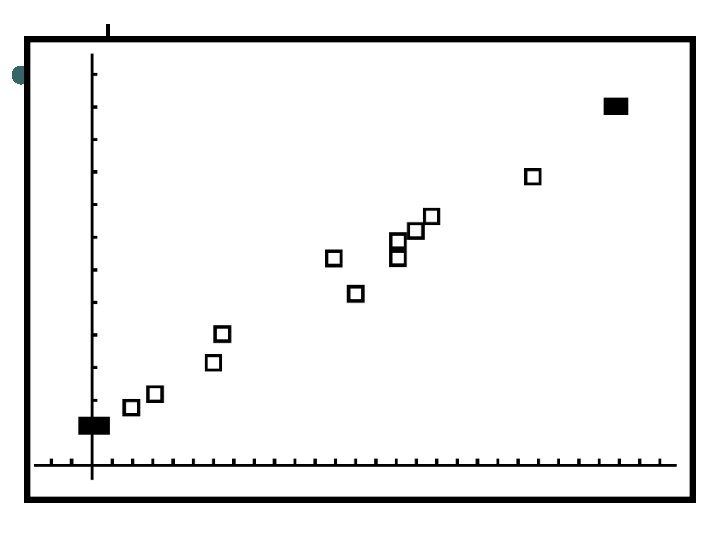
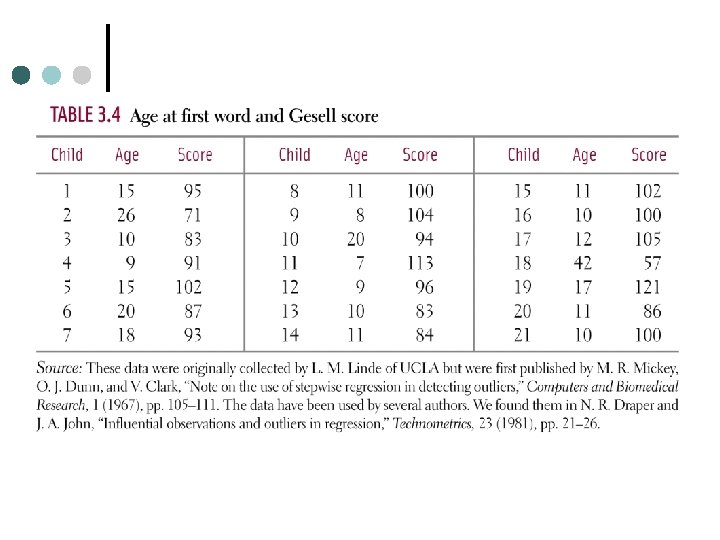
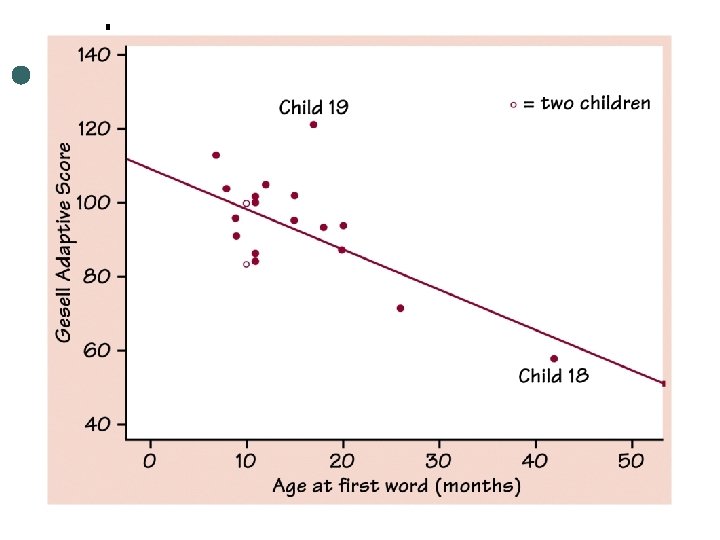
Influential Observations ¢ An observation is an influential observation for a statistical calculation if removing it would markedly change the result of the calculation.