Statistically Based Validation Acceptance Criteria Mark Varney Statistics

Statistically Based Validation Acceptance Criteria Mark Varney Statistics Program Manager Abbott Quality and Regulatory Abbott Park, IL

FDA Process Validation Guidance, Jan 2011 • Statistics mention 15 times • “statistical” • “statistics” • “statistically” • “statistician” – as a suggested team member • Clear that FDA expects more statistical thinking in validation • Some statisticians asked to be a team member may not be familiar with Quality Assurance applications and jargon • Acceptance Sampling • Statistical Process Control (SPC) • Process Capability 2 2

FDA Process Validation Guidance Overview Process Validation: The collection and evaluation of data, from the process design stage through commercial production, which establishes scientific evidence that a process is capable of consistently delivering quality product. 3 3

FDA Process Validation Guidance Overview The new Guidance specifies a lifecycle approach: • Stage 1 – Process Design • Statistically designed experiments (DOE) • Stage 2 – Process Qualification • Design of facility and equipment/utilities qualification • Process Performance Qualification (PPQ) • SPC; Variance components; Acceptance Sampling; CUDAL, etc. • Number of lots required is no longer specified as three • Must complete Stage 2 before commercial distribution • Stage 3 – Continued Process Verification (CPV) • Continual assurance the process is operating in a state of control • Data trending, SPC, Acceptance Sampling, etc. • Guidance recommends scrutiny of intra- and inter-batch variation 4 4

Statistical Acceptance Criteria for Validation Provide X% confidence that the requirement has been met Requirements: Process performance to consistently meet attributes related to identity, strength, quality, purity, and potency Statistical confidence required may be based on… • Risk • Scientific knowledge • Criticality of attribute (AQL, etc. ) • Prior / historical knowledge • Stage 1 knowledge • Revalidation • Is test an abuse test? 5 5

Three Common Situations Provide statistical confidence that… 1. A high percent of the population is within specification 2. A population parameter is within specification - Mean; Standard Deviation; RSD; Cpk/Ppk 3. A standard test (UDU, Dissolution, etc. ) will pass 6 6

Assure a High % of Population in Spec “ 90% confidence at least 99% of population meets spec” “ 90% confidence nonconformance rate <1%” “ 90% confidence for 99% reliability” Common statistical methods • Continuous data: Normal Tolerance Interval • Discrete data: High Confidence Binomial Sampling Plan 7 7

A Word about Confidence… Which sampling plan provides more confidence? 1. n=90, accept=0, reject=1 99% confidence ≥ 95% conforming 2. n=300, accept=0, reject=1 95% confidence ≥ 99% conforming 3. n=2300, accept=0, reject=1 90% confidence ≥ 99. 9% conforming What you want to be confident of is usually more important than how confident you want to be 8 8

Validation: High Degree of Assurance • Phrase “high degree of assurance” mentioned four times • “…the PPQ study needs to be completed successfully and a high degree of assurance in the process achieved before commercial distribution of a product. ” ICH Q 7 A GMP for APIs: • “A documented program that provides a high degree of assurance that a specific process, method, or system will consistently produce a result meeting pre-determined acceptance criteria. ” • Suggest 90% or 95% confidence is acceptable • This confidence is more related to Type II error and Power • Although α=0. 05 / 95% confidence is common for Type I error, it is not as common for power, where 80% and 90% also common. 9 9

Assure a High % is Within Spec Variables data: Normal Tolerance Interval* • Example: Show with 90% confidence that at least 99. 6% of powdered drug fill weights meet spec of 505 -535 mg. • Test n=50 bottles; 1 every 5 minutes for 4 hrs • Acceptance criterion: 90% confidence ≥ 99. 6% meet spec • Variables data with average, s. d. : use tolerance interval method • must be within specification limits • Why 99. 6%? Production AQL is 0. 4% for fill weight. *other methods may be used, such as variables sampling; may give lower Type I error 10 10

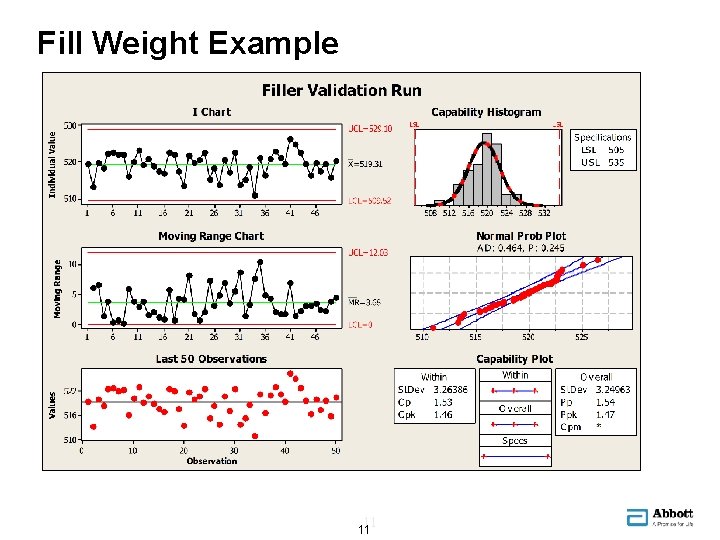
Fill Weight Example 11 11

Fill Weight Example • Process is in statistical control, normality not rejected • 90% confidence / 99. 6% coverage tolerance interval: • Pass: Tolerance interval lies within spec of 505 - 535 • We can be 90% confident ≥ 99. 6% of containers meet spec • Will be able to pass in-process 0. 4% AQL sampling • If process is stable, 90% confidence ≥ 95% of lots will pass • Engineer friendly: tables or software can be used 12 12

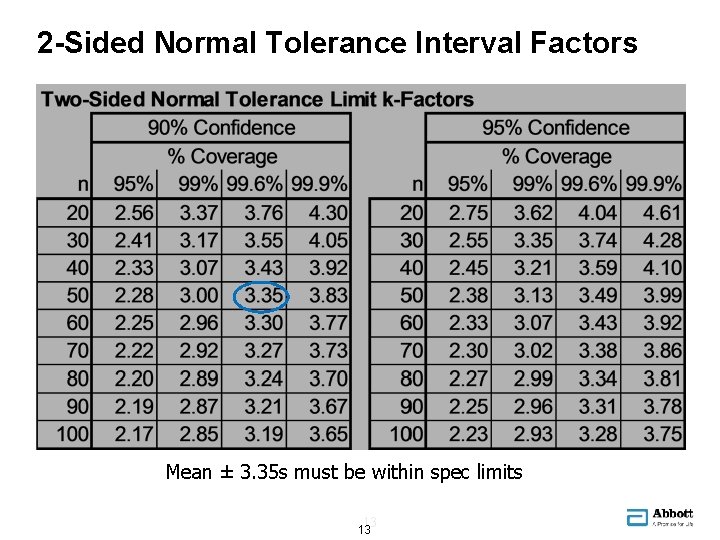
2 -Sided Normal Tolerance Interval Factors Mean ± 3. 35 s must be within spec limits 13 13

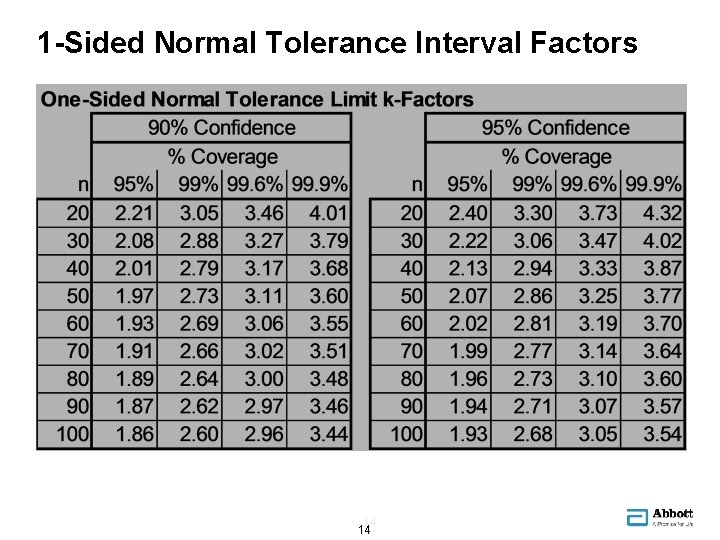
1 -Sided Normal Tolerance Interval Factors 14 14

A problem with most normality tests • • Need to check for normality to use normal tolerance interval Process quality data is often rounded • • • Or data is “granular” Most normality tests will interpret rounding as non-normality Example: n=100 from N(100, 1. 52) Unrounded 100. 071 98. 238 99. 122 Rounded 100 98 99 99. 190 100. 623 99 101 … , n=100 15 15

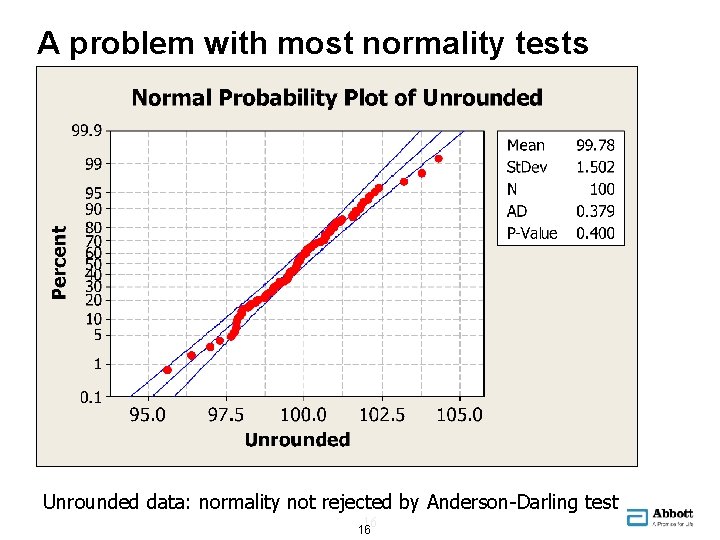
A problem with most normality tests Unrounded data: normality not rejected by Anderson-Darling test 16 16

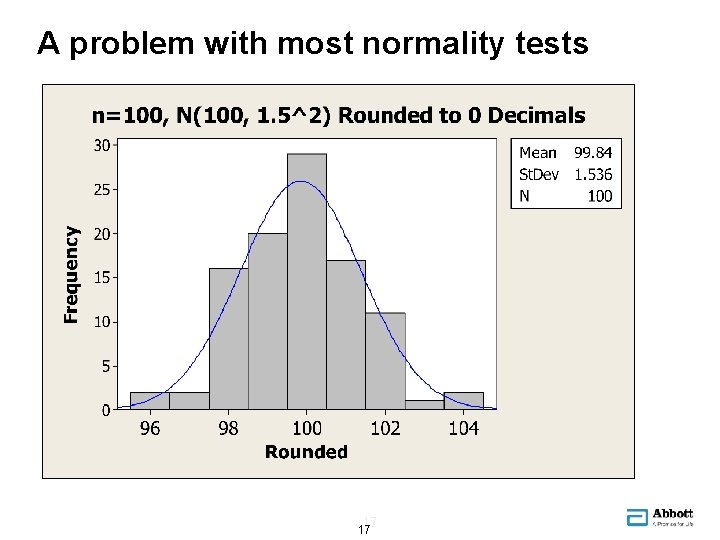
A problem with most normality tests 17 17

A problem with most normality tests • Rounding data causes most normality tests to fail • SAS 9. 2 Proc Univariate Tests: Unrounded Data Test Shapiro-Wilk Kolmogorov-Smirnov Cramer-von Mises Anderson-Darling --Statistic--W 0. 98874 D 0. 063184 W-Sq 0. 06213 A-Sq 0. 378299 -----p Value-----Pr < W 0. 5643 Pr > D >0. 1500 Pr > W-Sq >0. 2500 Pr > A-Sq >0. 2500 Rounded Data (to whole numbers) Test --Statistic--Shapiro-Wilk W 0. 956808 Kolmogorov-Smirnov D 0. 148507 Cramer-von Mises W-Sq 0. 358655 Anderson-Darling A-Sq 1. 926991 -----p Value-----Pr < W 0. 0024 Pr > D <0. 0100 Pr > W-Sq <0. 0050 Pr > A-Sq <0. 0050 18 18 OK Reject normality

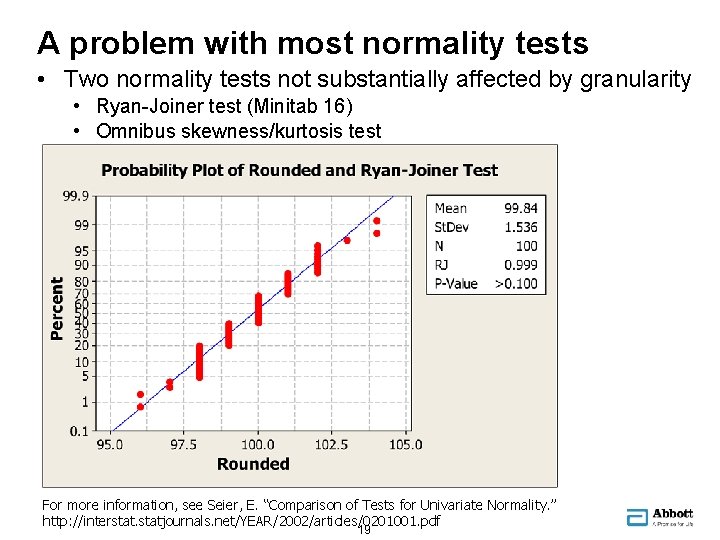
A problem with most normality tests • Two normality tests not substantially affected by granularity • Ryan-Joiner test (Minitab 16) • Omnibus skewness/kurtosis test For more information, see Seier, E. “Comparison of Tests for Univariate Normality. ” http: //interstatjournals. net/YEAR/2002/articles/0201001. pdf 19 19

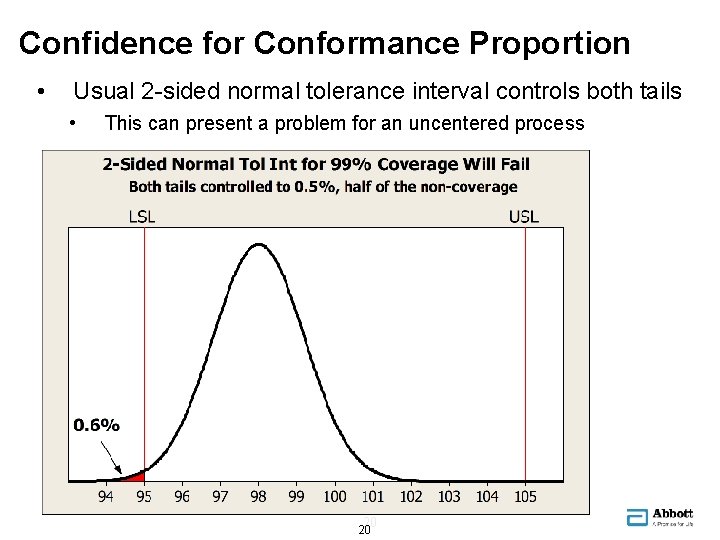
Confidence for Conformance Proportion • Usual 2 -sided normal tolerance interval controls both tails • This can present a problem for an uncentered process 20 20

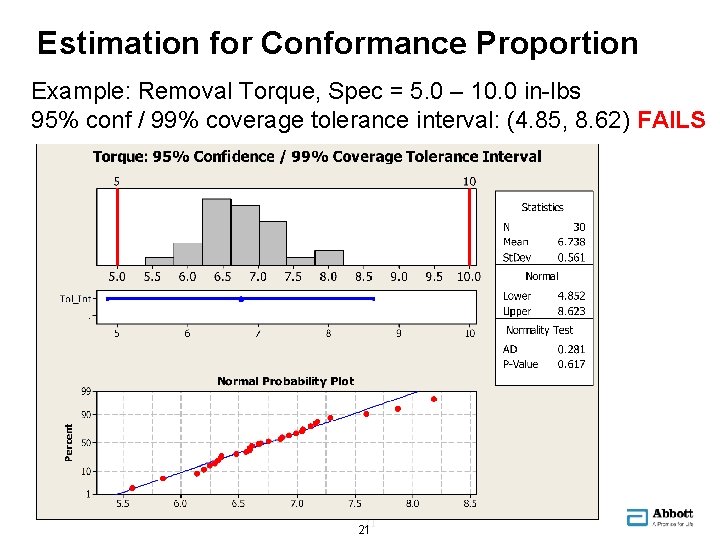
Estimation for Conformance Proportion Example: Removal Torque, Spec = 5. 0 – 10. 0 in-lbs 95% conf / 99% coverage tolerance interval: (4. 85, 8. 62) FAILS 21 21

Estimation for Conformance Proportion • Usual 2 -sided normal tolerance interval controls both tails • • This can present a problem for an uncentered process Can use estimation for proportion conforming • • • Also called bilateral conformance proportion Reduce probability of failing for uncentered processes Similar method used by ANSI Z 1. 9 for routine production sampling 22 22

Estimation for Conformance Proportion for Removal Torque: 95% confidence ≥ 99. 07% conforming: PASS Lee, H. , and Liao, C. “Estimation for Conformance Proportions in a Normal Variance Components Mode. ” Journal of Quality Technology, Jan. , 2012. Taylor, W. Distribution Analyzer, version 1. 2. 23 23

Random Effects Process Tolerance Limits • Overall process tolerance limits may be constructed to take between-lot variation into account • Example: Impurities Lot 1 Lot 2 Lot 3 n Mean 20 0. 047 20 0. 054 20 0. 050 St. Dev 0. 0113 0. 0055 0. 0087 Min 0. 018 0. 046 0. 035 Max 0. 069 0. 065 0. 068 • Approx 90% confidence / 95% coverage tolerance interval 1: Appears conservative • Usual 90/95% tolerance interval for all data combined: 0. 07 1 Krishnamoorthy, K. and Mathew, T. “One-Sided Tolerance Limits in Balanced and Unbalanced One. Way Random Models Based on Generalized Confidence Intervals. ” Technometrics, Vol. 46, No. 1, Feb. 2004. 24 24

What is an AQL? • AQL = "Acceptance Quality Limit“ • The quality level that would usually (95% of the time) be accepted by the sampling plan • RQL = "Rejection Quality Limit“ • The quality level that will usually (90% of the time) be rejected by the sampling plan • Also called LTPD (Lot Tolerance Percent Defective) • Also called LQ (Limiting Quality) 25 25

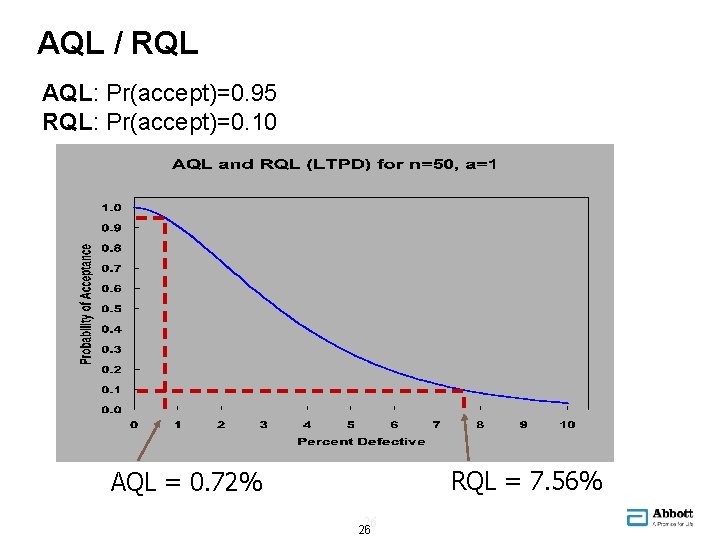
AQL / RQL AQL: Pr(accept)=0. 95 RQL: Pr(accept)=0. 10 RQL = 7. 56% AQL = 0. 72% 26 26

What is an AQL? Can be cast as a hypothesis test or confidence interval For routine acceptance sampling… Ho: p ≤ Assigned AQL H 1: p > Assigned AQL α=0. 05, “accept” lot if Ho not rejected But for validation… Ho: p > Assigned AQL H 1: p ≤ Assigned AQL or desired performance level α =1 -confidence; i. e. , 1 -. 90 =. 10 for 90% confidence Pass validation if Ho rejected 27 27

Typical AQLs in Pharma / Medical Devices Product Attribute Typical Assigned AQLs Critical 0. 04%, 0. 065%, 0. 15%, 0. 25% Major Functional 0. 25%, 0. 4%, 0. 65%, 1. 0% Minor Functional 0. 65%, 1. 0%, 1. 5% Cosmetic Visual 1. 5%, 2. 5%, 4%, 6. 5% • For validation, suggest 90% confidence that process ≤ assigned AQL • Why 90%? • Traditional probability used for RQL/LTPD/LQ • This means for validation the assigned AQL is treated as an RQL • If nonconforming rate is at AQL, will fail validation 90% of the time • Selection of the AQL more important than confidence selected • Much tighter than ANZI Z 1. 4/Z 1. 9 tightened (10 -20% confidence) 28 28

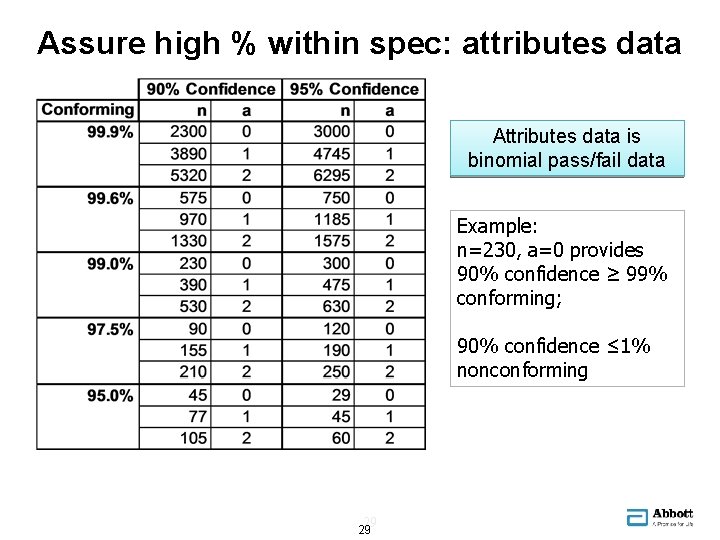
Assure high % within spec: attributes data Attributes data is binomial pass/fail data Example: n=230, a=0 provides 90% confidence ≥ 99% conforming; 90% confidence ≤ 1% nonconforming 29 29

Attributes Example for AQL: Fill Volume PPQ • Production assigned AQL is 1. 0% • AQL = “Acceptance Quality Limit” • Assigned based on risk assessment • If process is better than AQL, almost all mfg lots will be accepted • Validation: Show with 90% confidence that the process produces ≤ 1. 0% nonconforming units • Multi-head filler; we know data are non-normal • 90% confidence ≥ 99% are in spec • Medical devices: 90% confidence for 99% “reliability” • Assures that future AQL production sampling can be passed • If process is at the AQL, ~95% of lots will pass AQL sampling 30 30

Example: Fill Volume • Attributes plans: 90% confidence ≤ 1. 0% nonconforming Sampling Plan RQL 0. 10 n=230, acc=0, rej=1 1. 0% n=390, acc=1, rej=2 1. 0% n 1=250, a 1=0, r 1=2 n 2=250, a 2=1, r 2=2 1. 0% Z 1. 4 normal: n=80, acc=2 Z 1. 4 tightened: n=80, acc=1 • If the validation sampling plan passes… • We have 90% confidence the nonconforming rate is ≤ 1. 0% • ANSI Z 1. 4 plans provide far less than 90% confidence • Normal sampling: typically about 5% confidence • Tightened: typically about 15% confidence • Note: RQL=“Rejection Quality Limit” • Also called LTPD (Lot Tolerance Pct Defective) or LQ (Limiting Quality) 31 31

PV Acceptance Criteria for Attribute Types Attribute type Comment AQL attributes • Fill volume • Tablet defects • Extraneous matter, etc. ≥ 90% confidence that • Nonconformance rate ≤ assigned AQL Non-AQL attributes • Dissolution / UDU / Batch Assay • Other tests ≥ 90% confidence that… • USP test will be met ≥ 95% of the time • ≥ 99% of results in spec (critical) • ≥ 95% of results in spec (non-critical) Statistical Parameters • Mean / sigma / RSD(CV) • Cpk, Ppk ≥ 90% confidence that… • Mean / sigma / RSD in spec • Ppk ≥ 1. 0, 1. 33 or related to % coverage No within batch variation expected • p. H of a solution • Label copy text Statistics not usually necessary • May consider 3 X-10 X testing • Assess between lot variation 32 32

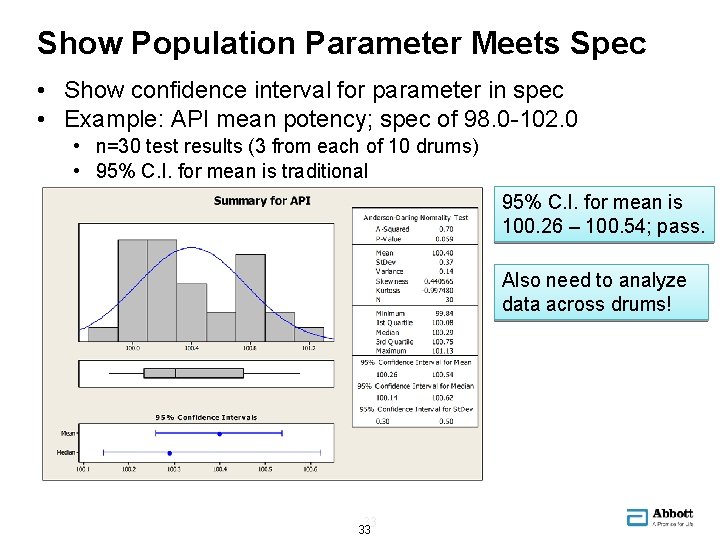
Show Population Parameter Meets Spec • Show confidence interval for parameter in spec • Example: API mean potency; spec of 98. 0 -102. 0 • n=30 test results (3 from each of 10 drums) • 95% C. I. for mean is traditional 95% C. I. for mean is 100. 26 – 100. 54; pass. Also need to analyze data across drums! 33 33

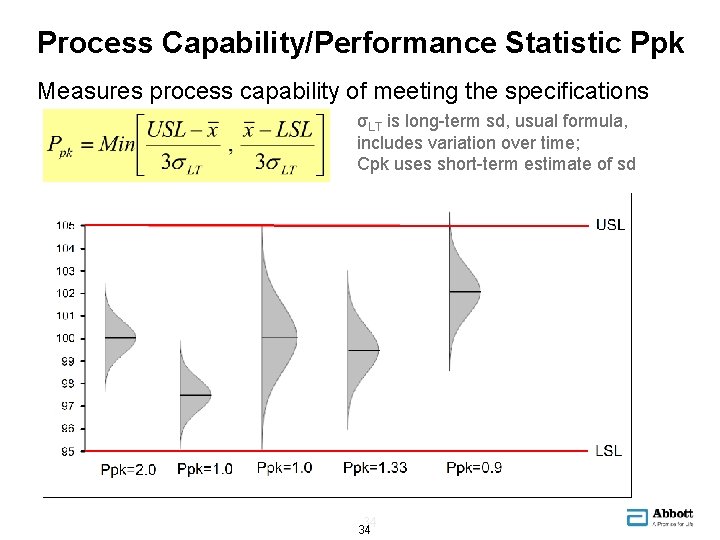
Process Capability/Performance Statistic Ppk Measures process capability of meeting the specifications σLT is long-term sd, usual formula, includes variation over time; Cpk uses short-term estimate of sd 34 34

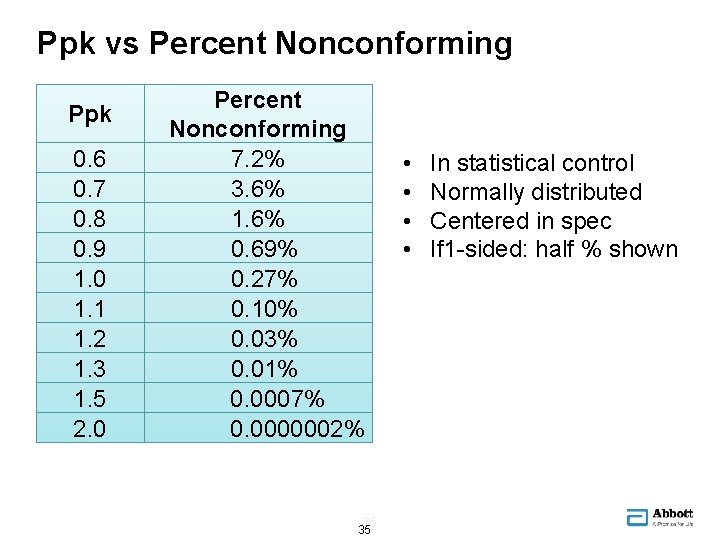
Ppk vs Percent Nonconforming Ppk 0. 6 0. 7 0. 8 0. 9 1. 0 1. 1 1. 2 1. 3 1. 5 2. 0 Percent Nonconforming 7. 2% 3. 6% 1. 6% 0. 69% 0. 27% 0. 10% 0. 03% 0. 01% 0. 0007% 0. 0000002% 35 35 • • In statistical control Normally distributed Centered in spec If 1 -sided: half % shown

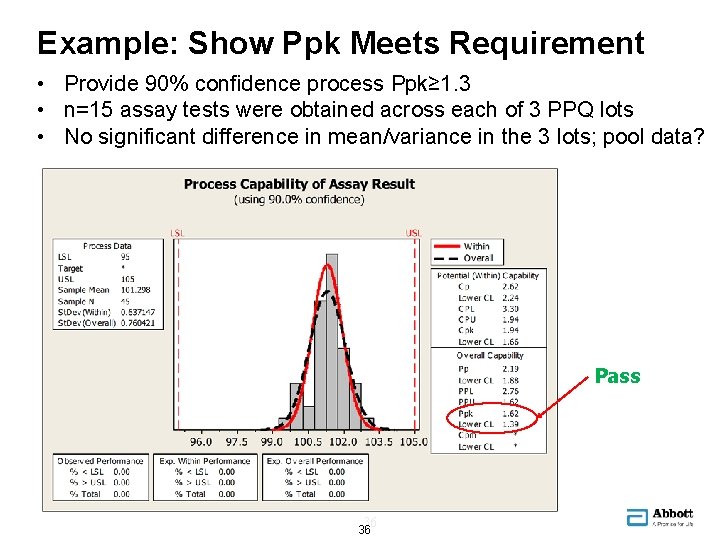
Example: Show Ppk Meets Requirement • Provide 90% confidence process Ppk≥ 1. 3 • n=15 assay tests were obtained across each of 3 PPQ lots • No significant difference in mean/variance in the 3 lots; pool data? Pass 36 36

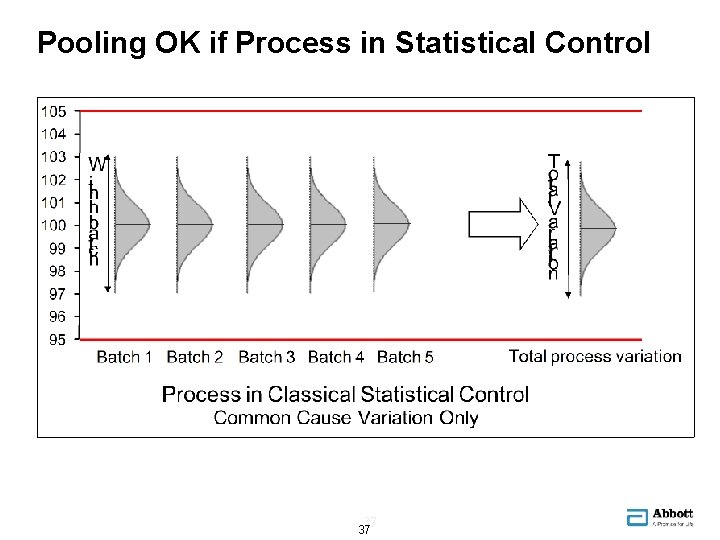
Pooling OK if Process in Statistical Control 37 37

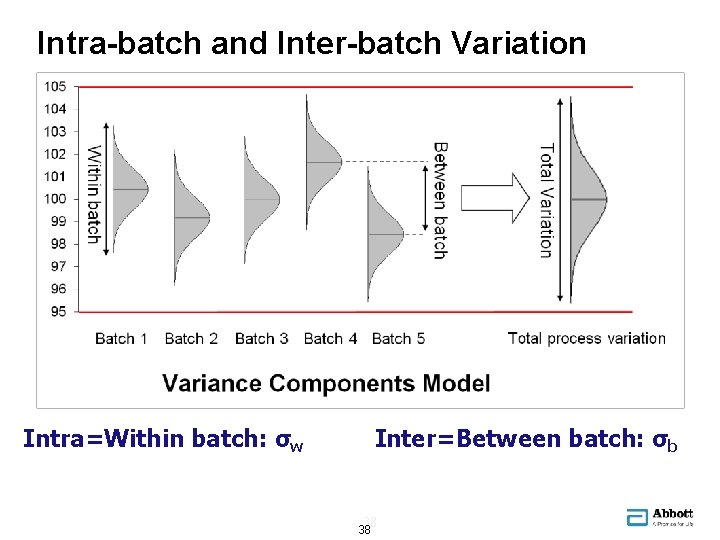
Intra-batch and Inter-batch Variation Intra=Within batch: σw Inter=Between batch: σb 38 38

Special Cause Variation 39 39

Ppk if Process is Not in Statistical Control • Use of Ppk is controversial if process not in statistical control 1 • • “Ppk has no meaningful interpretation” “statistical properties are not determinable” “a waste of engineering and management effort” Note: between-batch variation means not in classic statistical control • If variance components model holds, estimate Ppk with σw and σb • Usual confidence intervals from standards/software not applicable • Confidence interval must take degrees of freedom for σb into account • Difficulty in proving variance components model assumptions with small number of lots 1 Montgomery, Introduction to Statistical Quality Control 6 th edition, p 363 40 40

Potential problems with Ppk over multiple lots • Usual Ppk confidence interval assumes normal distribution and process stable / in statistical control • Any changes/trends within or between lots invalidates assumption • Often differences in mean between batches • Usual Ppk C. I. does not consider variance components • Example: 30 samples from each of 5 lots • (30 -1)x 5 = 145 degrees of freedom for within lot variation • (5 -1) = 4 degrees of freedom for between lot variation • ASTM reference E 2281 does not address this • Alternative: Show Ppk for each lot meets requirement for • 3 lots: ~87% overall confidence median process Ppk meets spec • 4 lots: ~94% confidence • 5 lots: ~97% confidence Or calculate a modified Ppk based on variance components C. I. 41 41

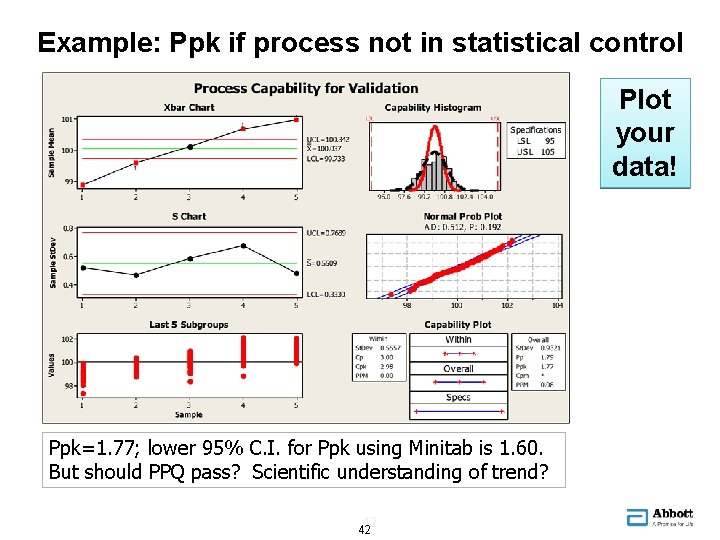
Example: Ppk if process not in statistical control Plot your data! Ppk=1. 77; lower 95% C. I. for Ppk using Minitab is 1. 60. But should PPQ pass? Scientific understanding of trend? 42 42

Assure a Standard Test will Pass • Example: Uniformity of Dosage Units (Content Uniformity) • Requirement: Pass USP‹ 905› Uniformity of Dosage Units • ≥ 90% confidence USP test would be passed ≥ 95% of the time (coverage) • • See Bergum 1 for specifics to determine acceptance criteria Why 90% confidence? Comparable to RQL probability. Why 95% coverage? Comparable to AQL probability for single test. Bayesian approach also available 2 1 Bergum, J. and Li, H. “Acceptance Limits for the New ICH USP 29 Content-Uniformity Test”, Pharmaceutical Technology , Oct 2, 2007 2 Leblond, D. , and Mockus, L. “Posterior Probability of Passing a Compendial Test. ” Presented at Bayes-Pharma 2012, Aachen, Germany. 43 43