Statistical Weather Forecasting 3 Daria Kluver Independent Study

Statistical Weather Forecasting 3 Daria Kluver Independent Study From Statistical Methods in the Atmospheric Sciences By Daniel Wilks

Let’s review a few concepts that were introduced last time on Forecast Verification

�Purposes of Forecast Verification �Forecast verification- the process of assessing the quality of forecasts. �Any given verification data set consists of a collection of forecast/observation pairs whose joint behavior can be characterized in terms of the relative frequencies of the possible combinations of forecast/observation outcomes. �This is an empirical joint distribution

The Joint Distribution of Forecasts and Observations �Forecast = �Observation = �The joint distribution of the forecasts and observations is denoted �This is a discrete bivariate probability distribution function associating a probability with each of the Ix. J possible combinations of forecast and observation.

�The joint distribution can be factored in two ways, the one used in a forecasting setting is: If yi has occurred, this is the �Called calibration-refinement factorization The unconditional probability of oj happening. distribution, which specifies �The refinement of a set of forecasts refers to the Specifies how often each the relative frequencies of possible weather of each dispersion ofevent the distributionusep(y i) of the forecast occurred on those occasions when the single forecast yi was issued, or how well each forecast is calibrated. values yi sometimes called the refinement of a forecast.

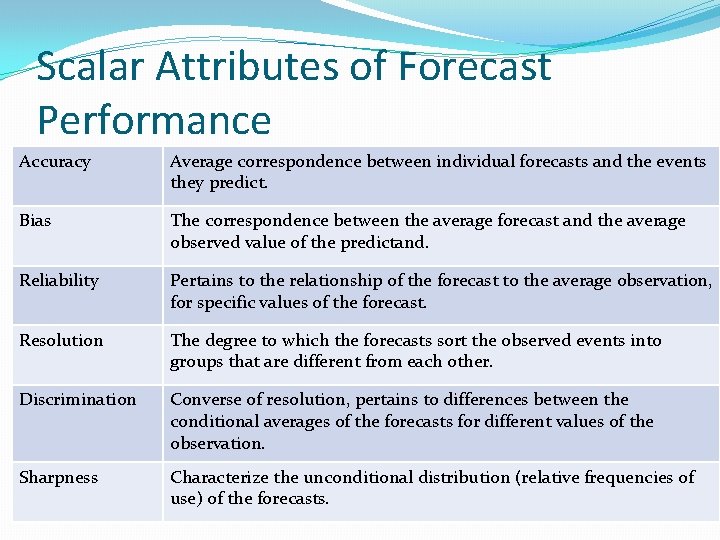
Scalar Attributes of Forecast Performance Accuracy Average correspondence between individual forecasts and the events they predict. Bias The correspondence between the average forecast and the average observed value of the predictand. Reliability Pertains to the relationship of the forecast to the average observation, for specific values of the forecast. Resolution The degree to which the forecasts sort the observed events into groups that are different from each other. Discrimination Converse of resolution, pertains to differences between the conditional averages of the forecasts for different values of the observation. Sharpness Characterize the unconditional distribution (relative frequencies of use) of the forecasts.

Forecast Skill �Forecast skill- the relative accuracy of a set of forecasts, wrt some set of standard control, or reference, forecast (like climatological average, persistence forecasts, random forecasts based on climatological relative frequencies) �Skill score- a percentage improvement over reference forecast. Accuracy of reference accuracy Accuracy that would be achieved by a perfect forecast.

On to new material… � 2 x 2 Contingency tables �Scalar attributes of contingency tables �Tornado example �NWS vs Weather. com vs climatology �Skill Scores �Probabilistic Forecasts �Multicategory Discrete Predictands �Continuous Predictands �Plots and score �Probability forecasts for multicategory events �Non-Probabilistic Field forecasts

Nonprobabilistic Forecasts of Discrete Predictands �Nonprobabilistic – contains unqualified statement that a single outcome will occur. Contains no expression of uncertainty.

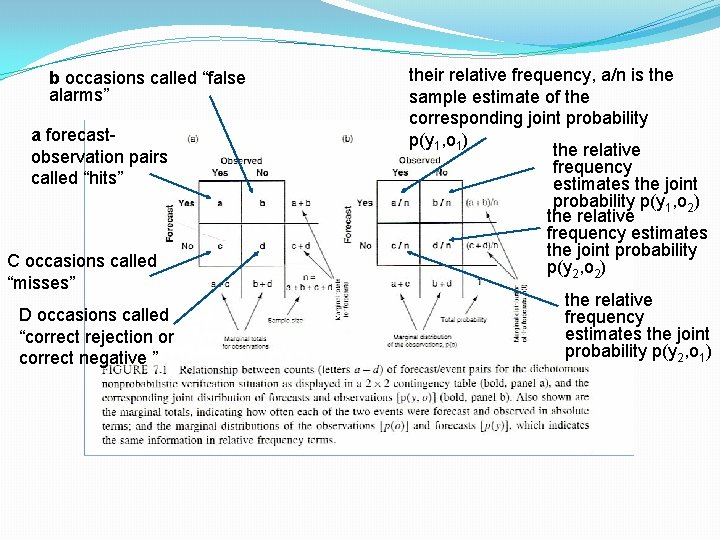
The 2 x 2 Contingency Table �The simplest joint distribution is from I=J=2. (or nonprobabilistic yes/no forecasts) �I=2 possible forecasts i=1 or y 1, event will occur i=2 or y 2, event will not occur �J=2 outcomes j=1 or o 1, event subsequently occurs j=2 or o 2, event doesn’t subsequently occur

b occasions called “false alarms” a forecastobservation pairs called “hits” C occasions called “misses” D occasions called “correct rejection or correct negative ” their relative frequency, a/n is the sample estimate of the corresponding joint probability p(y 1, o 1) the relative frequency estimates the joint probability p(y 1, o 2) the relative frequency estimates the joint probability p(y 2, o 1)

Scalar Attributes Characterizing 2 x 2 contingency tables � Accuracy – � proportion correct � Threat Score (TS) � Odds ratio � Bias� Comparison of the average forecast with the average observation � Reliability and Resolution� False Alarm Ratio � Discrimination� Hit rate � False Alarm Rate

NWS, weather. com, climatology example � 12 random nights from Nov 6 to Dec 1 �Will overnight lows be colder than or equal to freezing? forecast wx. com yes no yes 5 2 7 yes forecast NWS yes no yes forecast clim yes no forecaster no 0 5 5 5 7 no 6 1 7 0 5 5 6 6 0 5 5 1 11 no 1 6 7 a b c d PC TS odds ratio bias FAR H wx. com 5 0 2 5 0. 833 0. 71429 #DIV/0! 0. 71429 0 0. 714 NWS 6 0 1 5 0. 917 0. 85714 #DIV/0! 0. 85714 0 0. 857 clim 1 0 6 5 0. 14286 #DIV/0! 0. 14286 0 0. 143

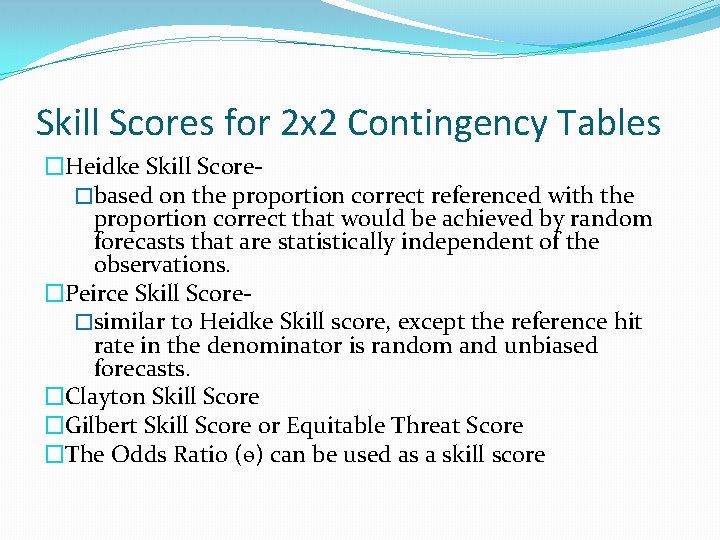
Skill Scores for 2 x 2 Contingency Tables �Heidke Skill Score�based on the proportion correct referenced with the proportion correct that would be achieved by random forecasts that are statistically independent of the observations. �Peirce Skill Score�similar to Heidke Skill score, except the reference hit rate in the denominator is random and unbiased forecasts. �Clayton Skill Score �Gilbert Skill Score or Equitable Threat Score �The Odds Ratio (ɵ) can be used as a skill score

Finley Tornado Forecasts example

Threat score gives a better comparison, because large number of no forecasts are ignored. TS=28/(28+72+23)=. 228 Odds ratio is 45. 3>1, suggesting better than random performance Bias ratio is B=1. 96, indicating that approximately twice as many tornados were forecast as actually occurred Gilbert pointed out that never Finley chose to evaluate his forecasts FAR = 0. 720, which expresses the fact that a fairly large fraction of the an forecasting a tornado produces using the proportion correct, PC = forecast tornados did not eventually occur. even higher proportion correct: , PC = (28+2680)/2803=0. 966. (0+2752)/2803=0. 982. Dominated by the correct no forecast. H=0. 549 and F=0. 0262, indicating that more than half of the actual tornados were forecast to occur, whereas a very small fraction of the non tornado cases falsely warned of a tornado. Skill Scores: HSS=0. 355 PSS=0. 523 CSS=0. 271 GSS=0. 216 Q=0. 957

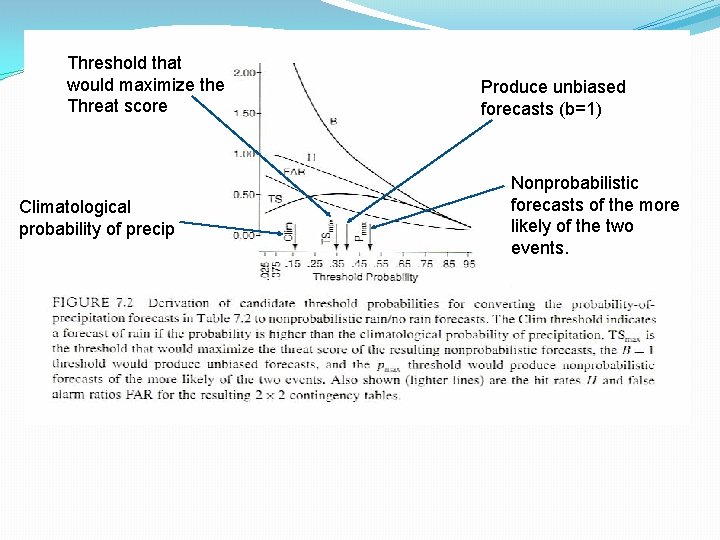
What if your data are Probabilistic? �For a dichotomous predictand, to convert from a probabilistic to a nonprobabilistic format requires selection of a threshold probability, above which the forecast will be “yes”. �Ends up somewhat arbitrary.

Threshold that would maximize the Threat score Climatological probability of precip Produce unbiased forecasts (b=1) Nonprobabilistic forecasts of the more likely of the two events.

Multicategory Discrete Predictands �Make into 2 x 2 tables R rain mix snow m s R non-rain Non-rain

Nonprobabilistic Forecasts of continuous predictands �It is informative to graphically represent aspects of the joint distribution of nonprobabilistic forecasts for continuous variables.

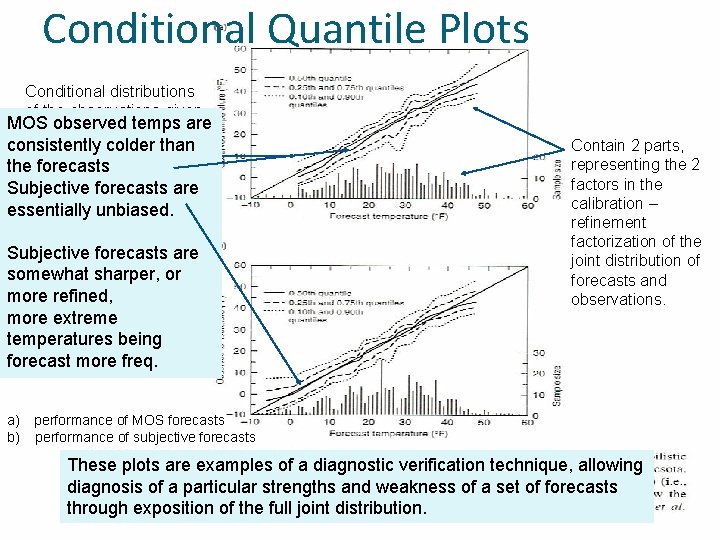
Conditional Quantile Plots Conditional distributions of the observations given MOS observedare temps are the forecasts consistently than representedcolder in terms of theselected forecasts quantiles, wrt the perfectforecasts 1: 1 line. are Subjective essentially unbiased. Subjective forecasts are somewhat sharper, or more refined, more extreme temperatures being forecast more freq. Contain 2 parts, representing the 2 factors in the calibration – refinement factorization of the joint distribution of forecasts and observations. a) performance of MOS forecasts b) performance of subjective forecasts These plots are examples of a diagnostic verification technique, allowing diagnosis of a particular strengths and weakness of a set of forecasts through exposition of the full joint distribution.

Scalar Accuracy Measures �Only 2 scalar measures of forecast accuracy for continuous predictands in common use. �Mean Absolute Error, and Mean Squared Error

Mean Absolute Error � �The arithmetic average of the absolute values of the differences between the members of each pair. �MAE = 0 if forecasts are perfect. Often used to verify temp forecasts.

Mean Squared Error � �The average squared difference between the forecast and observed pairs �More sensitive to larger errors than MAE �More sensitive to outliers �MSE = 0 for perfect �RMSE = which has same physical dimensions as the forecasts and observations �To calculate the bias of the forecast, compute the Mean Error: �

Skill Scores �Can be computed with MAE, MSE, or RMSE as the underlying accuracy statistics � Climatological value for day k �

Probability Forecasts of Discrete Predictands �The joint Distribution for Dichotomous Events �Not just using probabilities of 0 and 1 For each possible forecast probability we see the relative freq that forecast value was used, and the probability that the event o 1 occurred given the forecast yi

The Brier Score � Scalar accuracy measure for verification of probabilistic forecasts of dichotomous events � � This is the mean squared error of the probability forecasts, where o 1 = 1 if the event occurs and o 2 = 0 if the event doesn’t occur. � Perfect forecast BS = 0 less accurate forecasts receive higher BS. � Briar Skill Score:

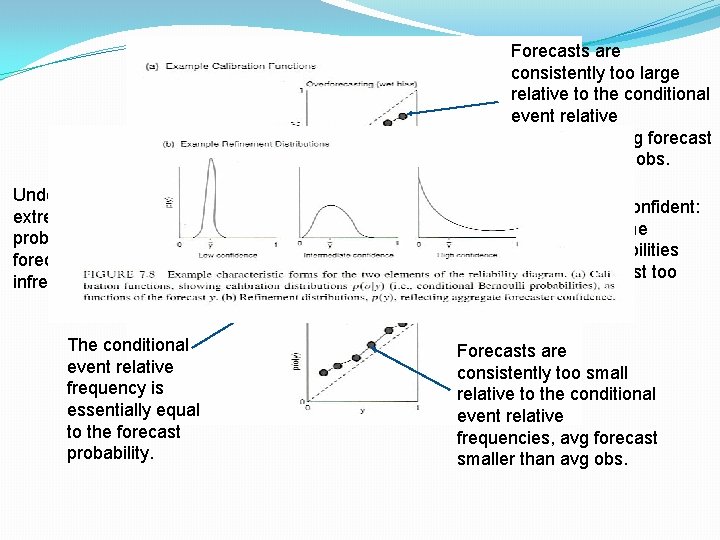
The Reliability Diagram �Is a graphical device that shows the full joint distribution of forecasts and observations for probability forecasts of a binary predictand, in terms of its calibration-refinement factorization �Allows diagnosis of particular strengths and weaknesses in a verification set.

Forecasts are consistently too large relative to the conditional event relative frequencies, avg forecast larger than avg obs. Underconfident: extreme probabilities forecast too infrequently The conditional event relative frequency is essentially equal to the forecast probability. Overconfident: extreme probabilities forecast too often Forecasts are consistently too small relative to the conditional event relative frequencies, avg forecast smaller than avg obs.

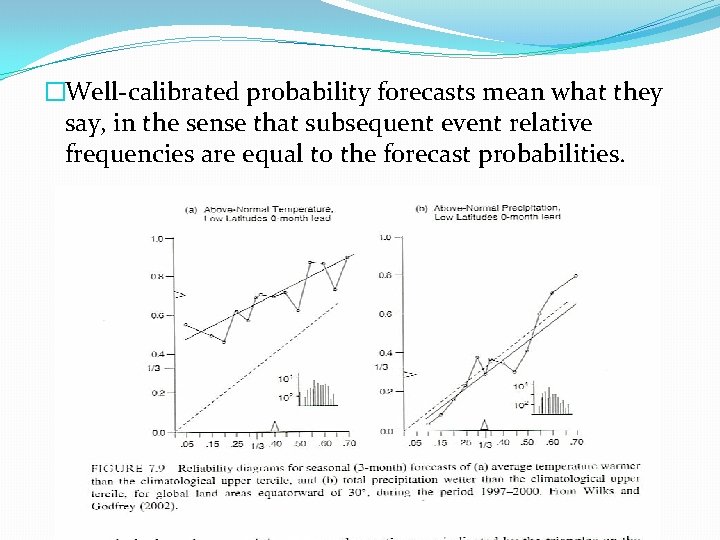
�Well-calibrated probability forecasts mean what they say, in the sense that subsequent event relative frequencies are equal to the forecast probabilities.

Hedging and Strictly proper scoring rules �If a forecaster is just trying to get the best score, they may improve scores by hedging, or gaming -> forecasting something other than our true belief in order to achieve a better score. �Strictly proper – a forecast evaluation procedure that awards a forecaster’s best expected score only when his or her true beliefs are forecast. �Cannot be hedged �Brier score �You can derive that it is proper, but I wont here.

Probability Forecasts for Multiple-category events �For multiple-category ordinal probability forecasts: � Verification should penalize forecasts increasingly as more probability is assigned to event categories further removed from the actual outcome. � Should be strictly proper. �Commonly used: � Ranked probability score (RPS)

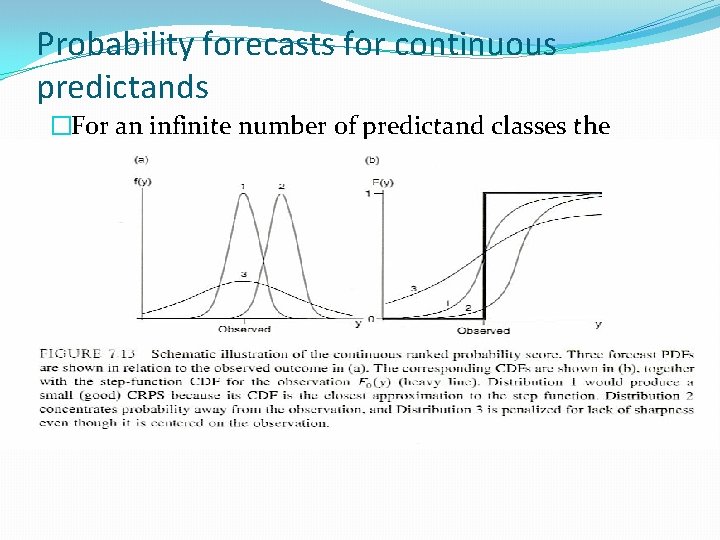
Probability forecasts for continuous predictands �For an infinite number of predictand classes the ranked probability score can be extended to the continuous case. �Continuous ranked probability score 1 �Strictly proper �Smaller values are better �It rewards concentration of probability around the step function located at the observed value.

Nonprobabilistic Forecasts of Fields �General considerations for field forecasts �Usually nonprobabilistic �Verification is done on a grid

�Scalar accuracy measures of these fields: �S 1 score, �Mean Squared Error, �Anomaly correlation

�Thank you for your participation throughout the semester �All presentations will be posted on my UD website �Additional information can be found in Statistical Methods in the Atmospheric Sciences (second edition) by Daniel Wilks