Statistical Thermodynamics Lecture 7 Distribution functions in classical

Statistical Thermodynamics Lecture 7: Distribution functions in classical monatomic liquids Dr. Ronald M. Levy ronlevy@temple. edu

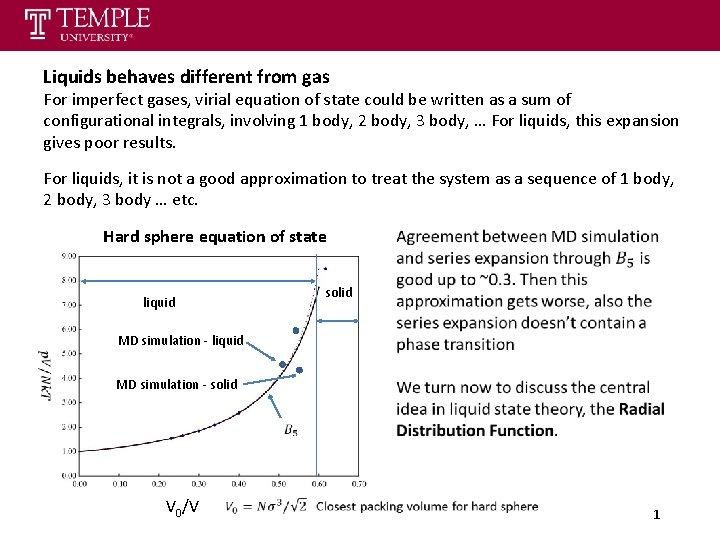
Liquids behaves different from gas For imperfect gases, virial equation of state could be written as a sum of configurational integrals, involving 1 body, 2 body, 3 body, … For liquids, this expansion gives poor results. For liquids, it is not a good approximation to treat the system as a sequence of 1 body, 2 body, 3 body … etc. Hard sphere equation of state liquid solid MD simulation - liquid MD simulation - solid V 0/V 1

N particle potential 1 Conformational partition function Integrated over n+1 to N 2 3 2

n particle correlation function 4 3

5 This equation defines the Conditional probability 4

N 1 6 5

6

Mean kinetic energy Mean potential energy 7

7 Expression for average internal energy in terms of pair correlation function 8

Double count N identical terms Averge potential energy between molecule 1 and molecules locates between r and r+dr 8 9

9 The factor V comes from the integration of dr coupling parameter integration 10 10

There are N-1 identical terms leading to N-1 identical integrals 11 Depends on coupling parameter 11

12 13 12

Potential of mean force(potential which gives the mean force) 14 13

15 Measure of the total influence of mol 1 and mol 2 Indirect part is the direct influence of particle 1 on 3. which in turn exerts its The direct correlation function influence on 2 directly or indirectly is defined by this equation Direct+indirect Can solve 2 equation interatively 14

Set of solute coordinates Potential energy of the system Set of solvent coordinates Defines W (PMF) 15

16

Solvent induced influence Intramolecular solute potential Solute charge distribution Poisson equation 17