Statistical Reporting Format Statistic Letter df obtained value

Statistical Reporting Format Statistic Letter (df) = obtained value, p decision Examples: A paired-samples t-test with 10 participants: t(9) = 3. 54, p<. 05 A one-way between-subjects ANOVA: F(2, 15) = 68. 20, p<. 05 If your results are NONSIGNIFICANT, you typically write p=NS. Example: F(2, 15) = 1. 32, p=NS

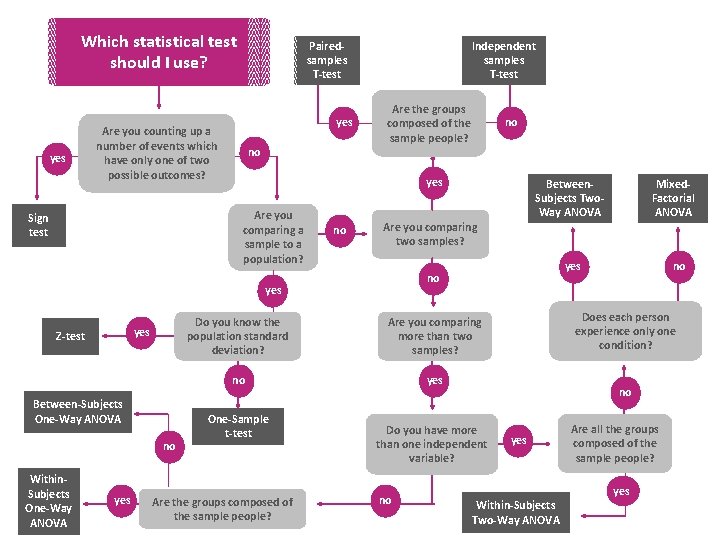
//\//\//\//\ //\//\//\//\ //\//\//\//\ //\//\//\//\ //\//\//\//\ //\//\//\//\ //\//\//\//\ //\//\//\//\ //\//\//\//\ Which statistical test should I use? yes Are you counting up a number of events which have only one of two possible outcomes? yes no Independent samples T-test Are the groups composed of the sample people? no yes Between-Subjects One-Way ANOVA no Within. Subjects One-Way ANOVA yes Are you comparing more than two samples? no yes Are the groups composed of the sample people? no Does each person experience only one condition? no Do you have more than one independent variable? no Mixed. Factorial ANOVA yes no Do you know the population standard deviation? One-Sample t-test Between. Subjects Two. Way ANOVA Are you comparing two samples? yes Z-test no yes Are you comparing a sample to a population? Sign test Pairedsamples T-test yes Within-Subjects Two-Way ANOVA Are all the groups composed of the sample people? yes

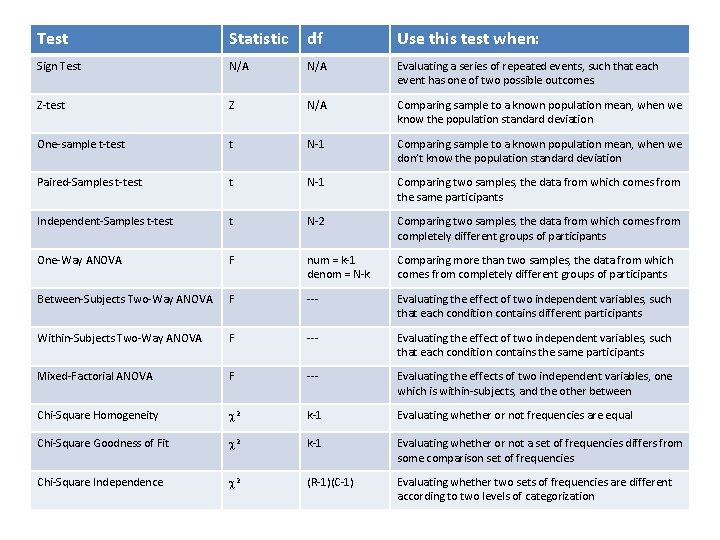
Test Statistic df Use this test when: Sign Test N/A Evaluating a series of repeated events, such that each event has one of two possible outcomes. Z-test Z N/A Comparing sample to a known population mean, when we know the population standard deviation One-sample t-test t N-1 Comparing sample to a known population mean, when we don’t know the population standard deviation Paired-Samples t-test t N-1 Comparing two samples, the data from which comes from the same participants Independent-Samples t-test t N-2 Comparing two samples, the data from which comes from completely different groups of participants One-Way ANOVA F num = k-1 denom = N-k Comparing more than two samples, the data from which comes from completely different groups of participants Between-Subjects Two-Way ANOVA F --- Evaluating the effect of two independent variables, such that each condition contains different participants Within-Subjects Two-Way ANOVA F --- Evaluating the effect of two independent variables, such that each condition contains the same participants Mixed-Factorial ANOVA F --- Evaluating the effects of two independent variables, one which is within-subjects, and the other between Chi-Square Homogeneity c 2 k-1 Evaluating whether or not frequencies are equal Chi-Square Goodness of Fit c 2 k-1 Evaluating whether or not a set of frequencies differs from some comparison set of frequencies Chi-Square Independence c 2 (R-1)(C-1) Evaluating whether two sets of frequencies are different according to two levels of categorization