Statistical Relational Learning Pedro Domingos Dept Computer Science

Overview l l l Motivation Some approaches Markov logic Application: Information extraction Challenges and

Motivation l l Most learners only apply to i. i. d. vectors But we

Some Approaches l l l Probabilistic logic [Nilsson, 1986] Statistics and beliefs [Halpern, 1990]

Markov Logic l l Logical formulas are hard constraints on the possible states of

Example: Friends & Smokers Two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B)

Markov Logic (Contd. ) l Probability of a state x: Weight of formula i

Key Ingredients l l Logical inference: Satisfiability testing Probabilistic inference: Markov chain Monte Carlo

Alchemy l Open-source software available at: alchemy. cs. washington. edu l l A new

Example: Information Extraction Parag Singla and Pedro Domingos, “Memory-Efficient Inference in Relational Domains” (AAAI-06).

Segmentation Author Title Venue Parag Singla and Pedro Domingos, “Memory-Efficient Inference in Relational Domains”

Entity Resolution Parag Singla and Pedro Domingos, “Memory-Efficient Inference in Relational Domains” (AAAI-06). Singla,

State of the Art l Segmentation l l Entity resolution l l l HMM

Types and Predicates token = {Parag, Singla, and, Pedro, . . . } field

Formulas Token(+t, i, c) => In. Field(i, +f, c) <=> In. Field(i+1, +f, c)

Formulas Token(+t, i, c) => In. Field(i, +f, c) ^ !Token(“. ”, i, c)

Challenges and Open Problems l l l l Scaling up learning and inference Model

Slides: 29

Download presentation

Statistical Relational Learning Pedro Domingos Dept. Computer Science & Eng. University of Washington

Overview l l l Motivation Some approaches Markov logic Application: Information extraction Challenges and open problems

Motivation l l Most learners only apply to i. i. d. vectors But we need to do learning and (uncertain) inference over arbitrary structures: trees, graphs, class hierarchies, relational databases, etc. All these can be expressed in first-order logic Let’s add learning and uncertain inference to first-order logic

Some Approaches l l l Probabilistic logic [Nilsson, 1986] Statistics and beliefs [Halpern, 1990] Knowledge-based model construction [Wellman et al. , 1992] l Stochastic logic programs [Muggleton, 1996] Probabilistic relational models [Friedman et al. , 1999] Relational Markov networks [Taskar et al. , 2002] Markov logic [Richardson & Domingos, 2004] l Bayesian logic [Milch et al. , 2005] l Etc. l l l

Markov Logic l l Logical formulas are hard constraints on the possible states of the world Let’s make them soft constraints: When a state violates a formula, It becomes less probable, not impossible Give each formula a weight (Higher weight Stronger constraint) More precisely: Consider each grounding of a formula

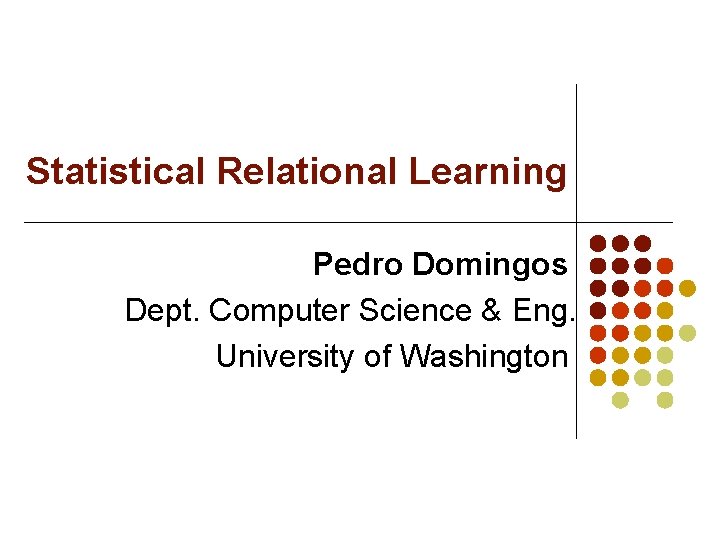
Example: Friends & Smokers Two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)

Markov Logic (Contd. ) l Probability of a state x: Weight of formula i l l No. of true groundings of formula i in x Most discrete statistical models are special cases (e. g. , Bayes nets, HMMs, etc. ) First-order logic is infinite-weight limit

Key Ingredients l l Logical inference: Satisfiability testing Probabilistic inference: Markov chain Monte Carlo Inductive logic programming: Search with clause refinement operators Statistical learning: Weight optimization by conjugate gradient

Alchemy l Open-source software available at: alchemy. cs. washington. edu l l A new kind of programming language Write formulas, learn weights, do inference Haven’t we seen this before? Yes, but without learning and uncertain inference

Example: Information Extraction Parag Singla and Pedro Domingos, “Memory-Efficient Inference in Relational Domains” (AAAI-06). Singla, P. , & Domingos, P. (2006). Memory-efficent inference in relatonal domains. In Proceedings of the Twenty-First National Conference on Artificial Intelligence (pp. 500 -505). Boston, MA: AAAI Press. H. Poon & P. Domingos, Sound and Efficient Inference with Probabilistic and Deterministic Dependencies”, in Proc. AAAI-06, Boston, MA, 2006. P. Hoifung (2006). Efficent inference. In Proceedings of the Twenty-First National Conference on Artificial Intelligence.

Segmentation Author Title Venue Parag Singla and Pedro Domingos, “Memory-Efficient Inference in Relational Domains” (AAAI-06). Singla, P. , & Domingos, P. (2006). Memory-efficent inference in relatonal domains. In Proceedings of the Twenty-First National Conference on Artificial Intelligence (pp. 500 -505). Boston, MA: AAAI Press. H. Poon & P. Domingos, Sound and Efficient Inference with Probabilistic and Deterministic Dependencies”, in Proc. AAAI-06, Boston, MA, 2006. P. Hoifung (2006). Efficent inference. In Proceedings of the Twenty-First National Conference on Artificial Intelligence.

Entity Resolution Parag Singla and Pedro Domingos, “Memory-Efficient Inference in Relational Domains” (AAAI-06). Singla, P. , & Domingos, P. (2006). Memory-efficent inference in relatonal domains. In Proceedings of the Twenty-First National Conference on Artificial Intelligence (pp. 500 -505). Boston, MA: AAAI Press. H. Poon & P. Domingos, Sound and Efficient Inference with Probabilistic and Deterministic Dependencies”, in Proc. AAAI-06, Boston, MA, 2006. P. Hoifung (2006). Efficent inference. In Proceedings of the Twenty-First National Conference on Artificial Intelligence.

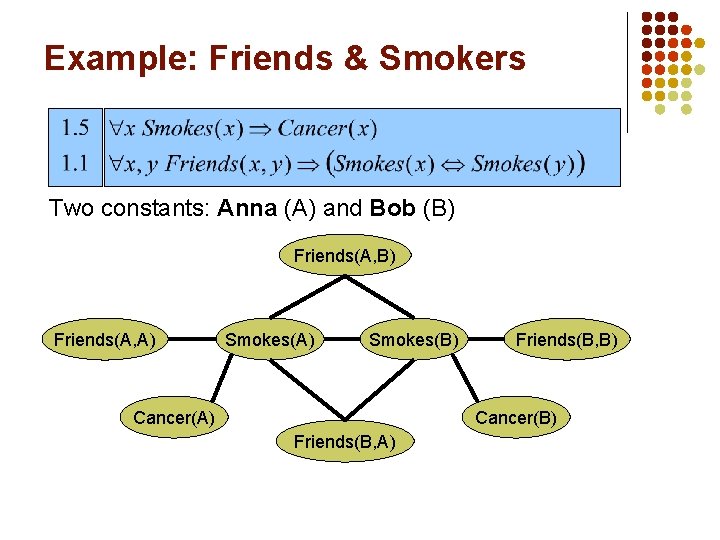
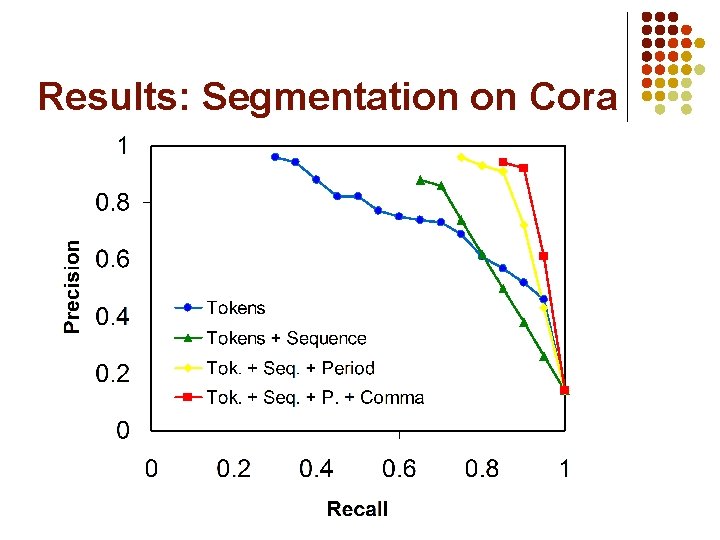
State of the Art l Segmentation l l Entity resolution l l l HMM (or CRF) to assign each token to a field Logistic regression to predict same field/citation Transitive closure Alchemy implementation: Seven formulas

Types and Predicates token = {Parag, Singla, and, Pedro, . . . } field = {Author, Title, Venue} citation = {C 1, C 2, . . . } position = {0, 1, 2, . . . } Token(token, position, citation) In. Field(position, field, citation) Same. Field(field, citation) Same. Cit(citation, citation)

Types and Predicates token = {Parag, Singla, and, Pedro, . . . } field = {Author, Title, Venue, . . . } citation = {C 1, C 2, . . . } position = {0, 1, 2, . . . } Token(token, position, citation) In. Field(position, field, citation) Same. Field(field, citation) Same. Cit(citation, citation) Optional

Formulas Token(+t, i, c) => In. Field(i, +f, c) <=> In. Field(i+1, +f, c) f != f’ => (!In. Field(i, +f, c) v !In. Field(i, +f’, c)) Token(+t, i, c) ^ In. Field(i, +f, c) ^ Token(+t, i’, c’) ^ In. Field(i’, +f, c’) => Same. Field(+f, c, c’) <=> Same. Cit(c, c’) Same. Field(f, c, c’) ^ Same. Field(f, c’, c”) => Same. Field(f, c, c”) Same. Cit(c, c’) ^ Same. Cit(c’, c”) => Same. Cit(c, c”)

Formulas Token(+t, i, c) => In. Field(i, +f, c) ^ !Token(“. ”, i, c) <=> In. Field(i+1, +f, c) f != f’ => (!In. Field(i, +f, c) v !In. Field(i, +f’, c)) Token(+t, i, c) ^ In. Field(i, +f, c) ^ Token(+t, i’, c’) ^ In. Field(i’, +f, c’) => Same. Field(+f, c, c’) <=> Same. Cit(c, c’) Same. Field(f, c, c’) ^ Same. Field(f, c’, c”) => Same. Field(f, c, c”) Same. Cit(c, c’) ^ Same. Cit(c’, c”) => Same. Cit(c, c”)

Results: Segmentation on Cora

Results: Matching Venues on Cora

Challenges and Open Problems l l l l Scaling up learning and inference Model design (aka knowledge engineering) Generalizing across domain sizes Continuous distributions Relational data streams Relational decision theory Statistical predicate invention Experiment design