Statistical Process Control What is a process Inputs

Statistical Process Control

What is a process? Inputs PROCESS Outputs A process can be described as a transformation of set of inputs into desired outputs.

Types of Measures • Measures where the metric is composed of a classification in one of two (or more) categories is called Attribute data. _ Good/Bad – Yes/No • Measures where the metric consists of a number which indicates a precise value is called Variable data. – Time – Miles/Hr 22 December 2021 3

Population Vs. Sample (Certainty Vs. Uncertainty) ã A sample is just a subset of all possible values sample population ã Since the sample does not contain all the possible values, there is some uncertainty about the population. Hence any statistics, such as mean and standard deviation, are just estimates of the true population parameters. 22 December 2021 4

WHY STATISTICS? THE ROLE OF STATISTICS ……… Statistics is the art of collecting, classifying, presenting, interpreting and analyzing numerical data, as well as making conclusions about the system from which the data was obtained. 22 December 2021 5

Descriptive Statistics is the branch of statistics which most people are familiar. It characterizes and summarizes the most prominent features of a given set of data (means, medians, standard deviations, percentiles, graphs, tables and charts. 22 December 2021 6

Inferential Statistics is the branch of statistics that deals with drawing conclusions about a population based on information obtained from a sample drawn from that population. 22 December 2021 7

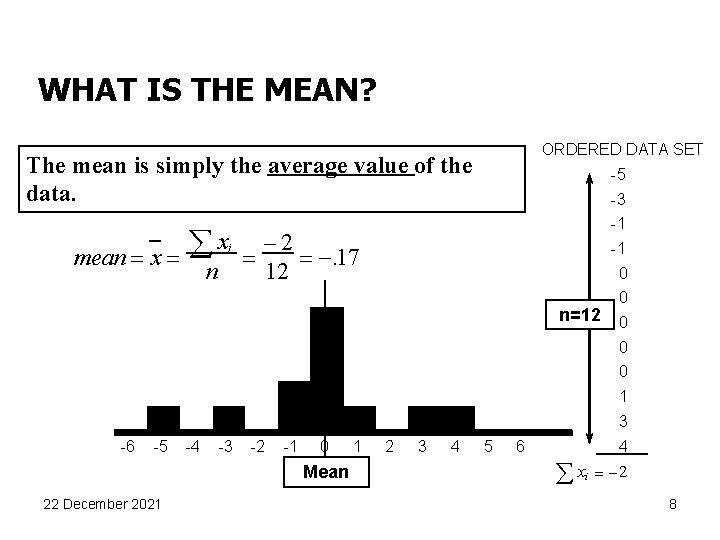
WHAT IS THE MEAN? ORDERED DATA SET The mean is simply the average value of the data. x å mean = x = i n -5 -3 -1 -2 = = -. 17 12 -1 0 n=12 0 0 1 3 -6 -5 -4 -3 -2 -1 0 Mean 22 December 2021 1 2 3 4 5 6 4 åx i = -2 8

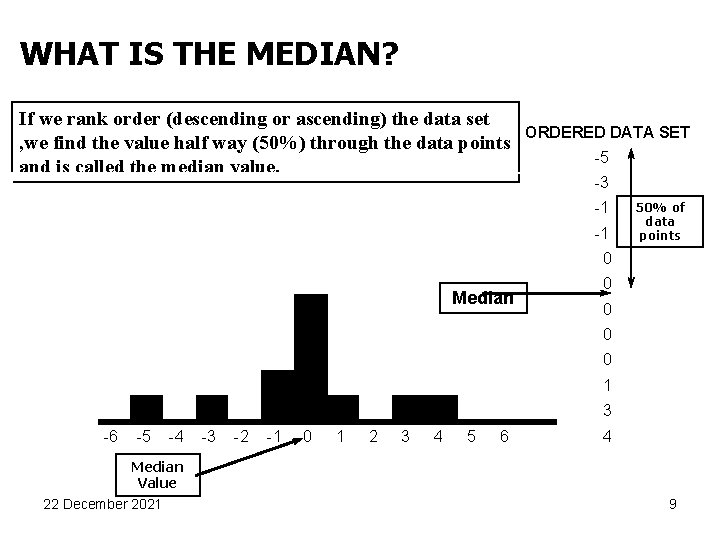
WHAT IS THE MEDIAN? If we rank order (descending or ascending) the data set , we find the value half way (50%) through the data points and is called the median value. ORDERED DATA SET -5 -3 -1 -1 50% of data points 0 Median 0 0 1 3 -6 -5 -4 Median Value 22 December 2021 -3 -2 -1 0 1 2 3 4 5 6 4 9

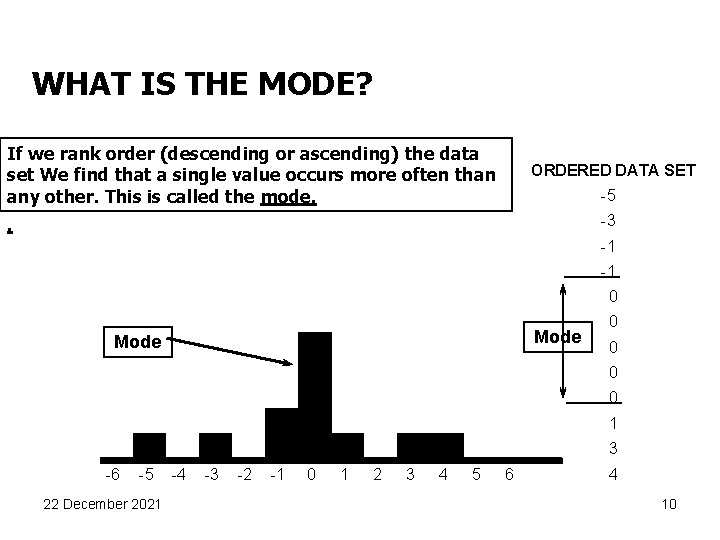
WHAT IS THE MODE? If we rank order (descending or ascending) the data set We find that a single value occurs more often than any other. This is called the mode. ORDERED DATA SET -5 -3 . -1 -1 0 Mode 0 0 1 3 -6 -5 22 December 2021 -4 -3 -2 -1 0 1 2 3 4 5 6 4 10

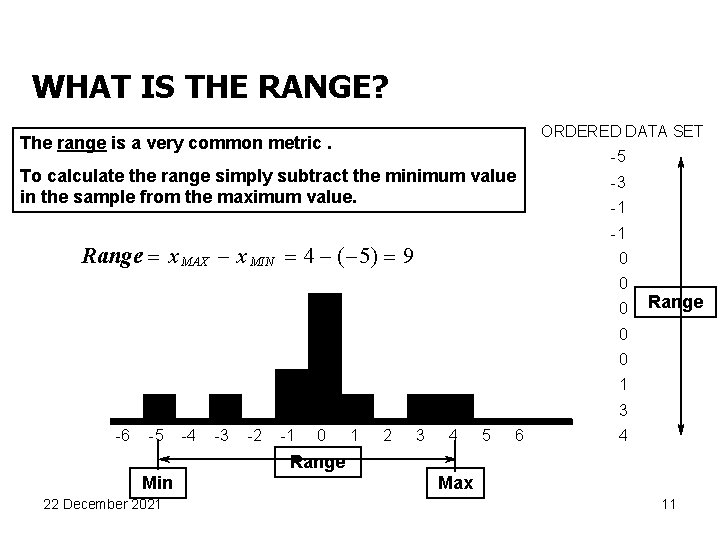
WHAT IS THE RANGE? ORDERED DATA SET The range is a very common metric. To calculate the range simply subtract the minimum value in the sample from the maximum value. -5 -3 -1 -1 Range = x MAX - x MIN = 4 - ( -5) = 9 0 0 0 Range 0 0 1 3 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 4 Range Min 22 December 2021 Max 11

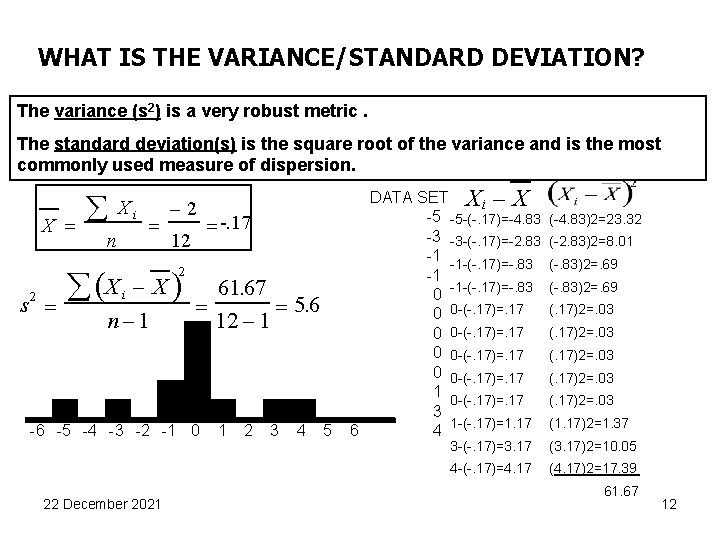
WHAT IS THE VARIANCE/STANDARD DEVIATION? The variance (s 2) is a very robust metric. The standard deviation(s) is the square root of the variance and is the most commonly used measure of dispersion. X = s 2 å Xi n X ( å = = -2 12 = -. 17 - X) 61. 67 = = 5. 6 n -1 12 - 1 2 i -6 -5 -4 -3 -2 -1 0 22 December 2021 1 2 3 4 5 DATA SET X i - X -5 -5 -(-. 17)=-4. 83 -3 -3 -(-. 17)=-2. 83 -1 -1 -(-. 17)=-. 83 0 0 0 -(-. 17)=. 17 1 0 -(-. 17)=. 17 3 1 -(-. 17)=1. 17 6 4 (-4. 83)2=23. 32 (-2. 83)2=8. 01 (-. 83)2=. 69 (. 17)2=. 03 (1. 17)2=1. 37 3 -(-. 17)=3. 17 (3. 17)2=10. 05 4 -(-. 17)=4. 17 (4. 17)2=17. 39 61. 67 12

Statistical Process Control (SPC) • Measures performance of a process • Uses mathematics (i. e. , statistics) • Involves collecting, organizing, & interpreting data • Objective: Regulate product quality • Used to – Control the process as products are produced – Inspect samples of finished products

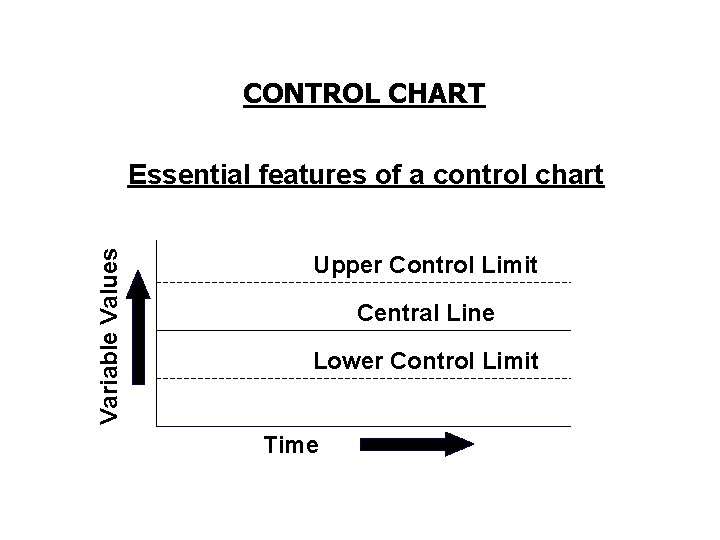
CONTROL CHART Functions of a Process Control System are Ø To signal the presence of assignable causes of variation Ø To give evidence if a process is operating in a state of statistical control

CONTROL CHART Variable Values Essential features of a control chart Upper Control Limit Central Line Lower Control Limit Time

Control Chart Purposes • Show changes in data pattern – e. g. , trends • Make corrections before process is out of control • Show causes of changes in data – Assignable causes • Data outside control limits or trend in data – Natural causes • Random variations around average

Quality Characteristics Variables Attributes 1. Characteristics that 1. Characteristics for which you focus on defects you measure, e. g. , 2. Classify products as either weight, length ‘good’ or ‘bad’, or count # 2. May be in whole or in defects – e. g. , radio works or not fractional numbers 3. Continuous random 3. Categorical or discrete variables random variables

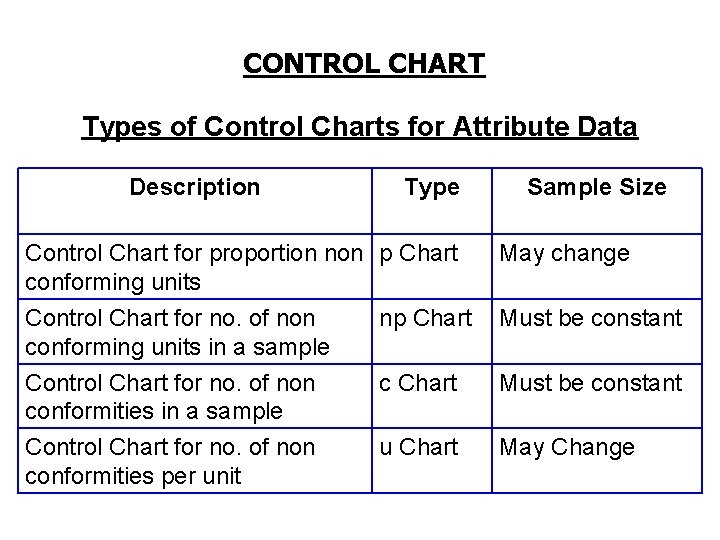
CONTROL CHART Types of Control Charts for Attribute Data Description Type Sample Size Control Chart for proportion non p Chart conforming units May change Control Chart for no. of non conforming units in a sample Control Chart for no. of non conformities per unit np Chart Must be constant c Chart Must be constant u Chart May Change

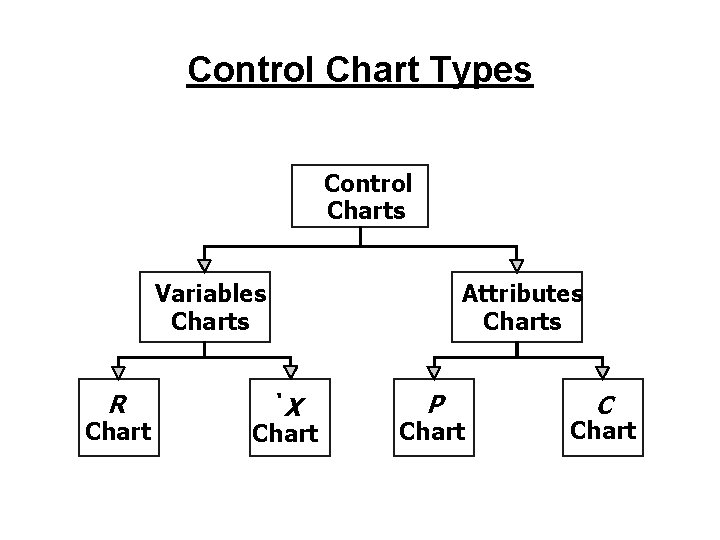
Control Chart Types Control Charts Variables Charts R Chart Attributes Charts `X Chart P Chart C Chart

X Chart • Type of variables control chart – Interval or ratio scaled numerical data • Shows sample means over time • Monitors process average and tells whether changes have occurred. These changes may due to 1. Tool wear 2. Increase in temperature 3. Different method used in the second shift 4. New stronger material • Example: Weigh samples of coffee & compute means of samples; Plot

R Chart • Type of variables control chart – Interval or ratio scaled numerical data • Shows sample ranges over time – Difference between smallest & largest values in inspection sample • Monitors variability in process, it tells us the loss or gain in dispersion. This change may be due to: 1. Worn bearing 2. A loose tool 3. An erratic flow of lubricant to machine 4. Sloppiness of machine operator • Example: Weigh samples of coffee & compute ranges of samples; Plot

Construction of X and R Charts • Step 1: Select the Characteristics for applying a control chart. • Step 2: Select the appropriate type of control chart. • Step 3: Collect the data. • Step 4: Choose the rational sub-group i. e Sample • Step 5: Calculate the average ( X) and range R for each sample. • Step 6: Cal Average of averages of X and average of range(R)

Construction of X and R Charts • Steps 7: Cal the limits for X and R Charts. • Steps 8: Plot Centre line (CL) UCL and LCL on the chart • Steps 9: Plot individual X and R values on the chart. • Steps 10: Check whether the process is in control (or) not. • Steps 11: Revise the control limits if the points are outside.

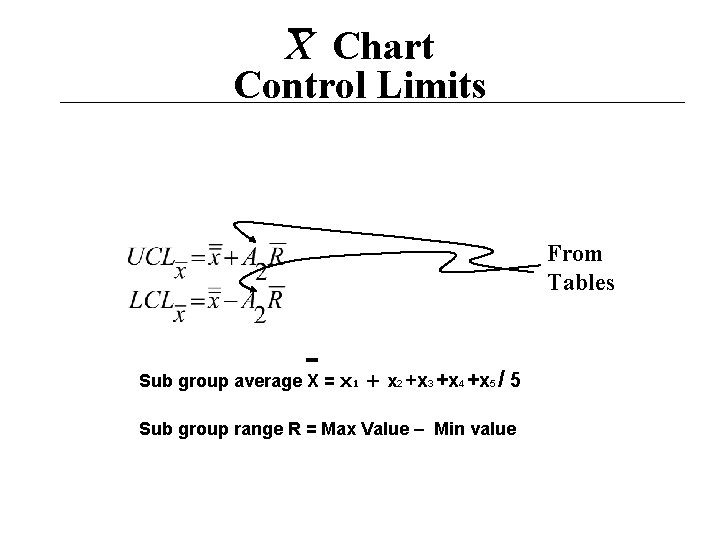
X Chart Control Limits From Tables Sub group average X = x 1 + x 2 +x 3 +x 4 +x 5 / 5 Sub group range R = Max Value – Min value

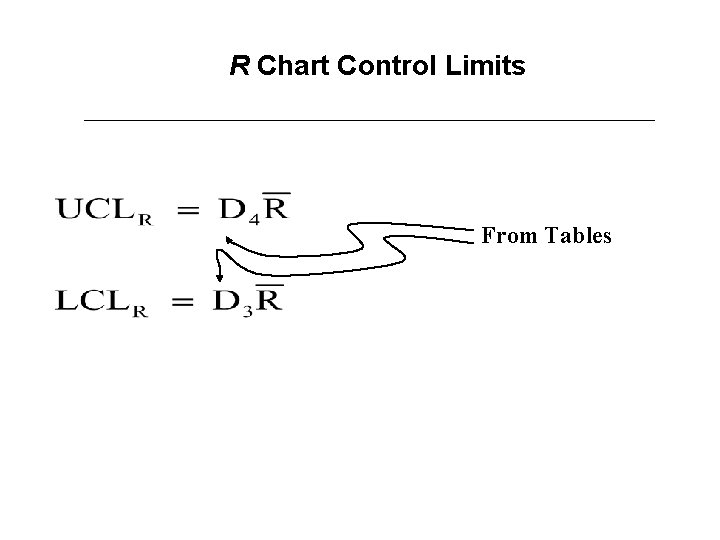
R Chart Control Limits From Tables

Problem 8. 1 from TQM by V. Jayakumar Page No 8. 5

p Chart for Attributes • Type of attributes control chart – Nominally scaled categorical data • e. g. , good-bad • Shows % of nonconforming items • Example: Count # defective chairs & divide by total chairs inspected; Plot – Chair is either defective or not defective

p Chart • p = np / n where p = Fraction of Defective np = no of Defectives n = No of items inspected in sub group p= Avg Fraction Defective = ∑np/ ∑n = CL

p Chart Control Limits z = 3 for 99. 7% limits

Purpose of the p Chart Identify and correct causes of bad quality The average proportion of defective articles submitted for inspection, over a period. To suggest where X and R charts to be used. Determine average Quality Level.

Problem • Problem 9. 1 Page no 9. 3 TQM by V. Jayakumar

np CHART P and np are quiet same Whenever subgroup size is variable, p chart is used. If sub group size is constant, then np is used. FORMULA: Central Line CLnp = n p Upper Control Limit, UCLnp = n p +3√ n p (1 - p ) Lower Control Limit, LCLnp = n p -3 √ n p (1 - p ) Where p = ∑ np/∑n =Average Fraction Defective n = Number of items inspected in subgroup.

Problem • Problem No 9. 11 page No 9. 11 in TQM by V. Jayakumar

c Chart • Type of attributes control chart – Discrete quantitative data • Shows number of nonconformities (defects) in a unit – Unit may be chair, steel sheet, car etc. – Size of unit must be constant • Example: Count no of defects (scratches, chips etc. ) in each chair of a sample of 100 chairs; Plot

c Chart Control Limits Use 3 for 99. 7% limits