Statistical Process Control Production and Process Management Where

Statistical Process Control Production and Process Management

Where to Inspect in the Process • Raw materials and purchased parts – supplier certification programs can eliminate the need for inspection • Finished goods – for customer satisfaction, quality at the source can eliminate the need for inspection • Before a costly operation – not to waste costly labor or machine time on items that are already defective • Before an irreversible process – in many cases items can be reworked up to a certain point, beyond that point • Before a covering process – painting can mask deffects

Process stability and process capability • Statistical process control (SPC) is used to evaluate process output to decide if a process is „in control” or if corrective action is needed. • Quality Conformance: does the output of a process conform to specifications • These are independent

Variation of the process • Random variation (or chance) – natural variation in the output of a process, created by countless minor factors, we can not affect these factors • Assignable variation – in process output a variation whose cause can be identified. • In control processes – contains random variations • Out of control processes – contains assigneable variations

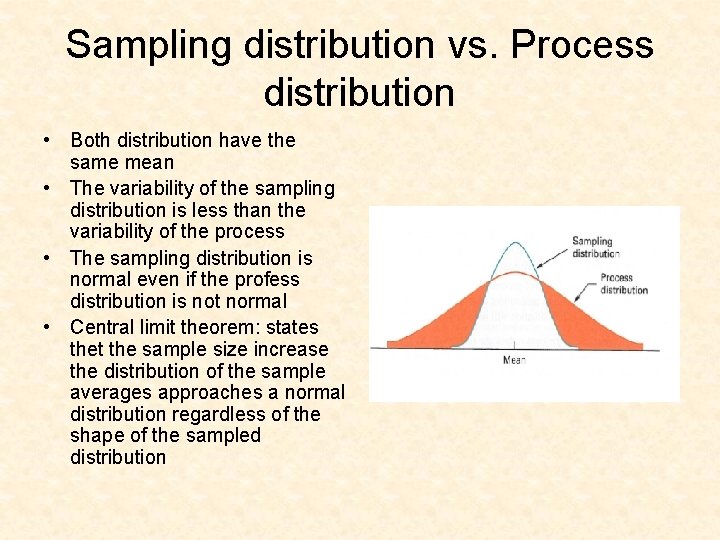
Sampling distribution vs. Process distribution • Both distribution have the same mean • The variability of the sampling distribution is less than the variability of the process • The sampling distribution is normal even if the profess distribution is not normal • Central limit theorem: states thet the sample size increase the distribution of the sample averages approaches a normal distribution regardless of the shape of the sampled distribution

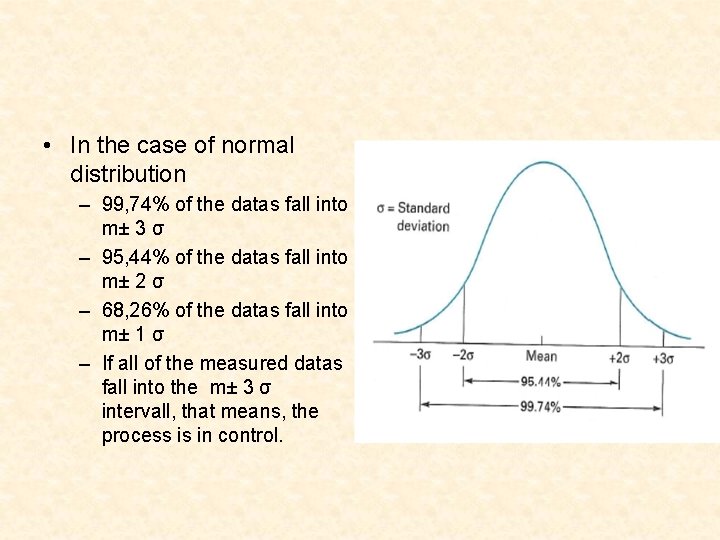
• In the case of normal distribution – 99, 74% of the datas fall into m± 3 σ – 95, 44% of the datas fall into m± 2 σ – 68, 26% of the datas fall into m± 1 σ – If all of the measured datas fall into the m± 3 σ intervall, that means, the process is in control.

Sampling • Random sampling – Each itemhas the same probability to be selected – Most common – Hard to realise • Systhematic sampling – According to time or pieces • Rational subgoup – Logically homogeneous – If variation among different subgroups is not accounted fo, then an unawanted source of nonrandom variation is being introduced – Morning and evening measurement in hospitals (body temperature)

• Variables – generate data that are measured (continuus scale, for example length of a part) • Attributes – generate data that are counted (number of defective parts, number of calls per day)

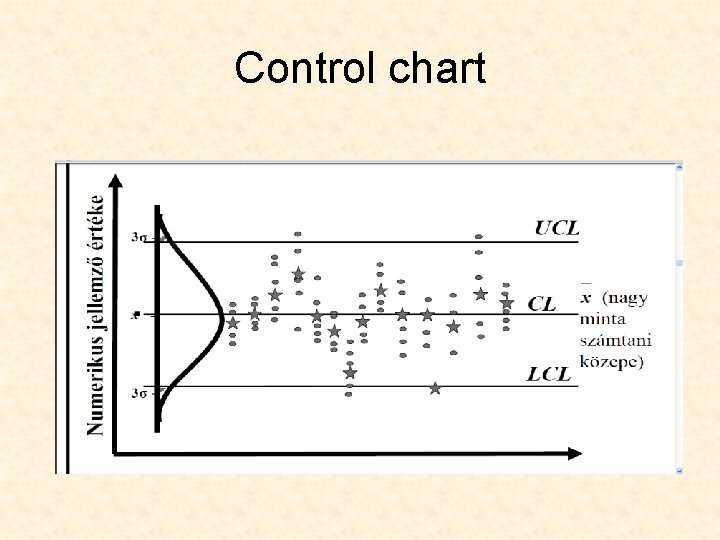
Control limits • The dividing lines between random and nonrandom deviation from the mean of the distribution • UCL – Upper Control limit • CL – Central line • LCL – lower Control limit • This is counted from the process itself. It is not the same as specification limits!

Specification limits • USL – Upper specification limit • LCL – lower specification limit • These reflect external specifications, and determined in advance, it is not counted from the process.

Control chart

Hypothesis test • H 0 = the process is stable Decision Stable Reality not stable Stable OK Type I error (risk of the producer) not stable Type II error risk OK of the costumer)

• Type I error – concluding a process is not in control when it is actually is – producers risk – it takes unnecessary burden on the producer who must searh fot something is not there • Type II error – concluding a process is in control when it is actually not – customers risk – because the producer didn’t realise something is wrong and passes it on to the costumer

Control charts

and R – mean and range chart • Sample size – n=4 or n=5 can be handled well, with short itervals, • Sampling freuency – to reflec every affects as chenges of shifts, operators etc. • Number of samples – 25 or more

• mean • range • n is the sample size • Means of samples’ means • Means of ranges • m is the number of samples

Control limits A 2, D 3, D 4 are constants and depends on the sample size

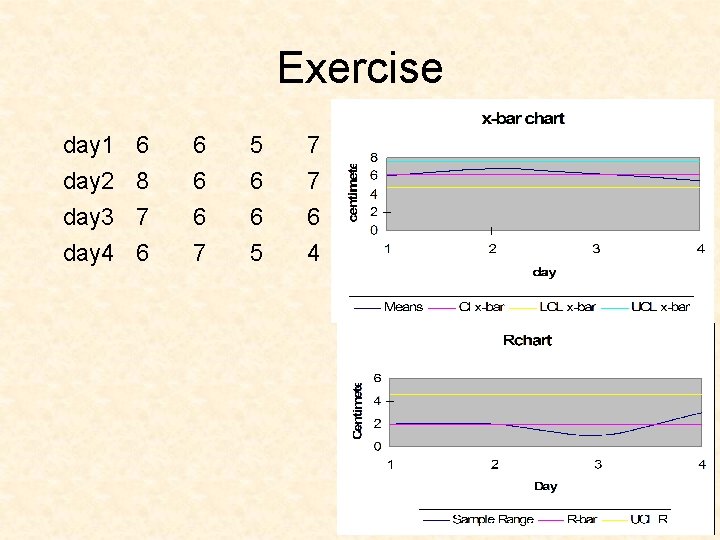
Exercise day 1 day 2 day 3 day 4 6 8 7 6 6 7 5 6 6 5 7 7 6 4

Control charts for attributes • When the process charasterictic is counted rather than measured • p-chart – fraction of defective items in a sample • c-chart – number of defects per unit

p-chart • p-average fraction defective in the population • P and σ can be counted from the samples • min 25 samples • Big samlpe size is needed (50 -200 pieces) – n • Number of defective item –np • If the LCL is negativ, lower limit will be 0.

Exercise

• z=3, 00 • p=220/(20*100)=0, 11 • σ=(0, 11(10, 11)/100)1/2=0, 03 • UCL=0, 11+3*0, 03=0, 2 • LCL=0, 11 -3*0, 3=0, 02

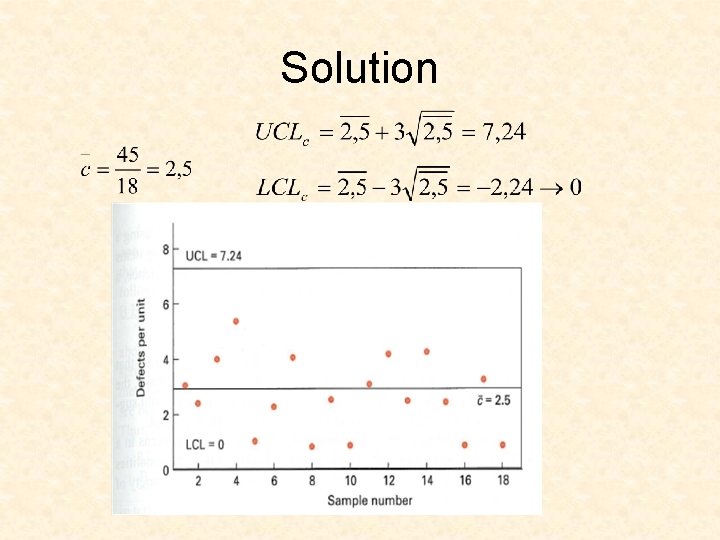
c-chart • To control the occurrences (defects) per unit • c 1, c 2 a number of defects per unit, k is the number of units

Exercise

Solution

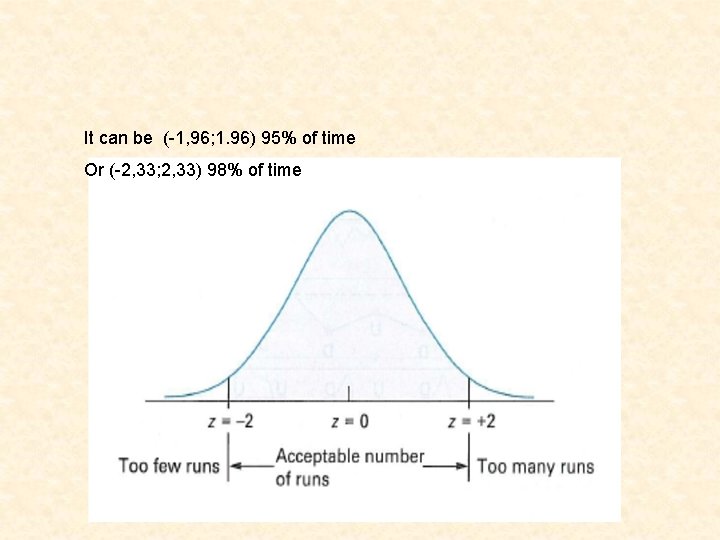
Run test • Determine – Runs up and down (u/d) – Above and below median (med) • Count the number of runs and compared with the number of runs that would be expected in a completely random series. – E(r)med=N/2+1 – E(r)u/d=(2 N-1)/3 , ahol N number of observations or data points, E(r) expected number of runs • Determine the standard deviation • Too few or too maní runs can be an indication of nonrandomness • Meghatározni a z értékeket: – Z=(observed number of runs-expected number of runs)/standard deviation • counted z must be fall into the interval of (-2; 2) to accept nonrandomness (this means that the 95, 5% of the time random process will produce an observed number of runs within 2σ of the expected number)

It can be (-1, 96; 1. 96) 95% of time Or (-2, 33; 2, 33) 98% of time

Example

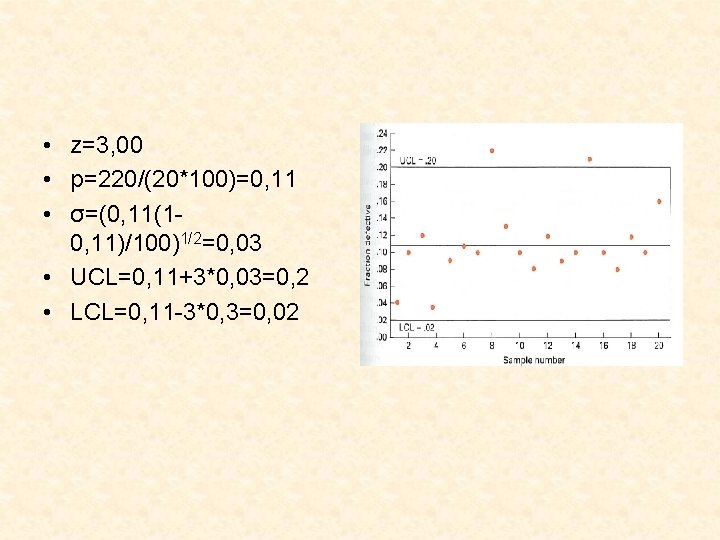
Solution • • E(r)med=N/2+1=20/2+1=11 E(r)u/d=(2 N-1)/3=(2*20 -1)/3=13 σmed=[(N-1)/4]1/2=[(20 -1)/4]1/2=2, 18 σu/d= =[(16 N-29)/90]1/2 =[(16*20 -29)/90]1/2=1, 80 zmed=(10 -11)/2, 18=-0, 46 Zu/d=(17 -13)/1, 8=2, 22 Although the median test doesn’t reveal any pattern, the up down test does.

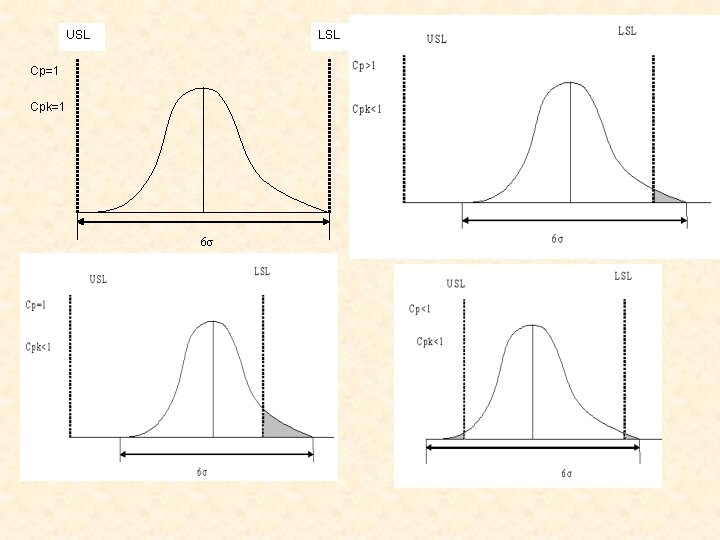
Index of process capability • CP (capability process) – it refers to the inherent variability of process output relative to the variation allowed by designed specifications • the higher CP the best capablity • I the case of CP>1 the process can fulfill the requirements • It make sense when the process is centered

Process capability when process is not centered • - means of samples’ means • - standard deviation

Process capability when process is not centered II • When sampling is not achievable, than for the total population

USL LSL Cp=1 Cpk=1 6σ

• When the process is not centered the is the fault of operator but when standard deviation is higher than the tolerance limit, managers must interfer in a new machine is needed , Cp>1 Cp<1 Cpk>1 process capacity is proper It can’t occure Cpk<1 Process capacity is Managers not proper it is the responsible for workers fault

Exercise • For an overheat projector, the thickness of a component is specified to be between 30 and 40 millimeters. Thirty samples of components yielded a grand mean ( ) 34 mm, with a standard deviation ( ) 3, 5 mm. Calculate the process capability index by following the steps previously outlined. If the process is not highly capable, what proportion of product will not conform?

Solution • • • Cpu=(40 -34)/3*3, 5=0, 57 Cpl=(34 -30)/3+3, 5=0, 38 Cpk=0, 38 Process is out of control To determine number of products use table of normal distribution • Z=(x- )/ =(30 -34)/3, 5=-1, 14 • Z=40 -34/3, 5=1, 71 • 0, 1271+0, 0436=0, 1707 17, 07% of products doesn’t meet specification

Thank you for your attention