Statistical Parametric Mapping Will Penny Wellcome Trust Centre

Statistical Parametric Mapping Will Penny Wellcome Trust Centre for Neuroimaging, University College London, UK LSTHM, UCL, Jan 14, 2009

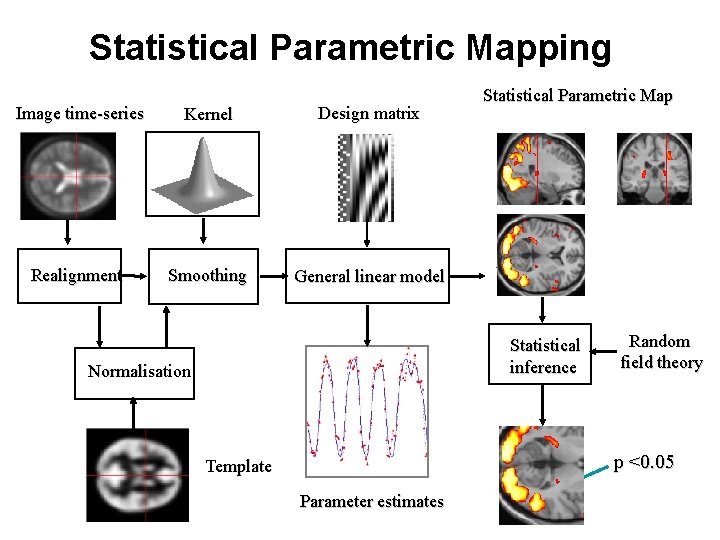
Statistical Parametric Mapping Image time-series Kernel Design matrix Realignment Smoothing General linear model Statistical Parametric Map Statistical inference Normalisation Random field theory p <0. 05 Template Parameter estimates

Outline • Voxel-wise General Linear Models • Random Field Theory • Bayesian modelling

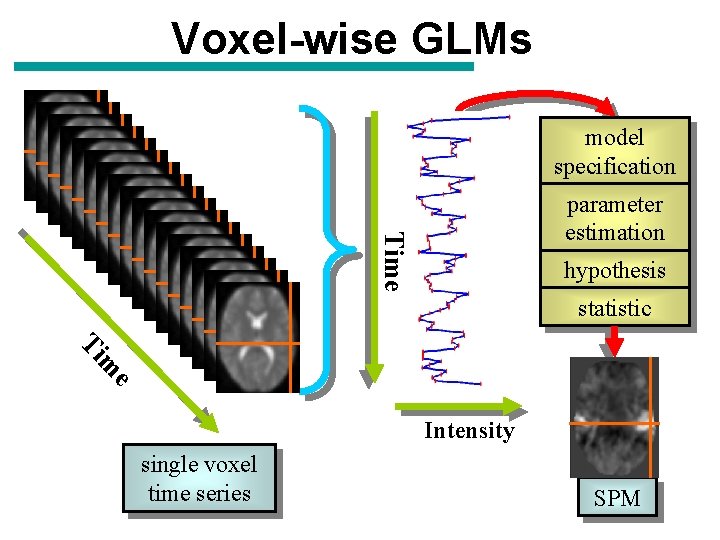
Voxel-wise GLMs model specification Time parameter estimation hypothesis statistic Ti e m Intensity single voxel time series SPM

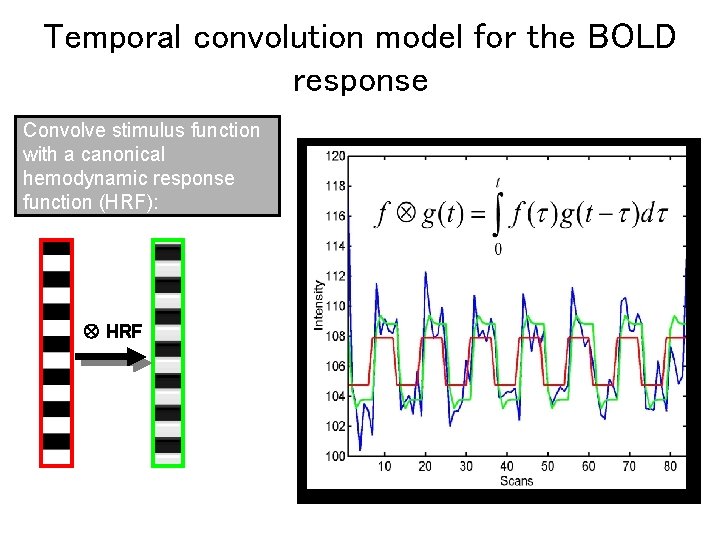
Temporal convolution model for the BOLD response Convolve stimulus function with a canonical hemodynamic response function (HRF): HRF

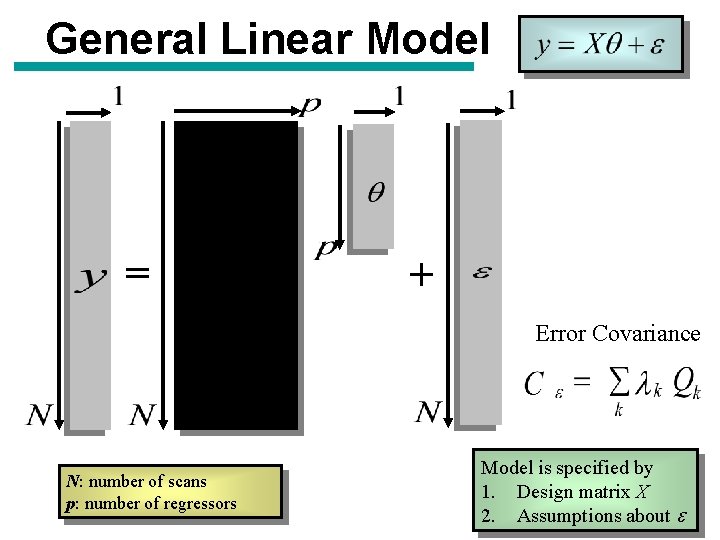
General Linear Model = + Error Covariance N: number of scans p: number of regressors Model is specified by 1. Design matrix X 2. Assumptions about e

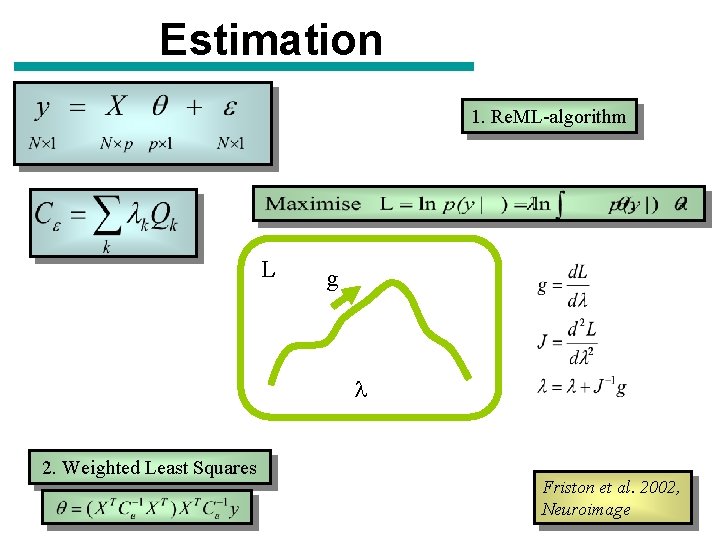
Estimation 1. Re. ML-algorithm L g l 2. Weighted Least Squares Friston et al. 2002, Neuroimage

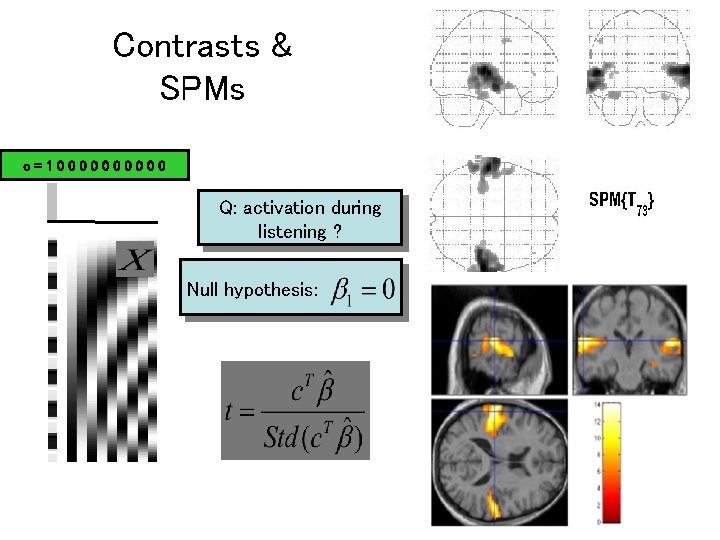
Contrasts & SPMs c=100000 Q: activation during listening ? Null hypothesis:

Outline • Voxel-wise General Linear Models • Random Field Theory • Bayesian modelling

Inference for Images Noise Signal+Noise

Use of ‘uncorrected’ p-value, a=0. 1 11. 3% 12. 5% 10. 8% 11. 5% 10. 0% 10. 7% 11. 2% 10. 2% 9. 5% Percentage of Null Pixels that are False Positives Using an ‘uncorrected’ p-value of 0. 1 will lead us to conclude on average that 10% of voxels are active when they are not. This is clearly undesirable. To correct for this we can define a null hypothesis for images of statistics.

Family-wise Null Hypothesis FAMILY-WISE NULL HYPOTHESIS: Activation is zero everywhere If we reject a voxel null hypothesis at any voxel, we reject the family-wise Null hypothesis A FP anywhere in the image gives a Family Wise Error (FWE) Family-Wise Error (FWE) rate = ‘corrected’ p-value

Use of ‘uncorrected’ p-value, a=0. 1 Use of ‘corrected’ p-value, a=0. 1 FWE

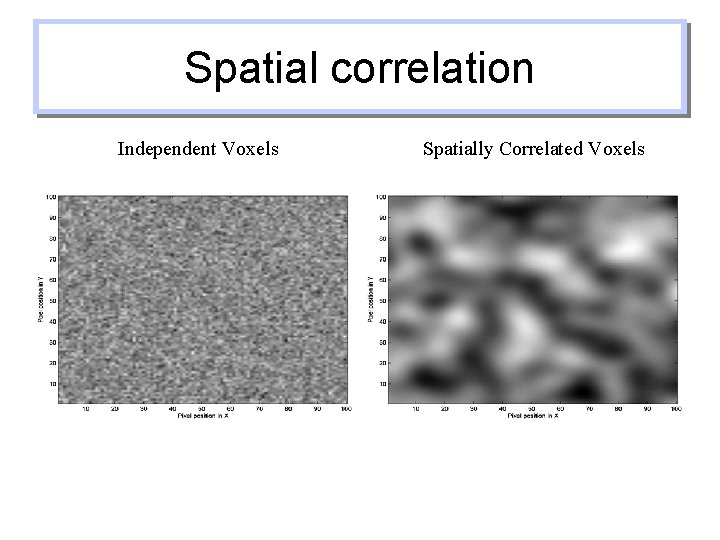
Spatial correlation Independent Voxels Spatially Correlated Voxels

Random Field Theory • Consider a statistic image as a discretisation of a continuous underlying random field • Use results from continuous random field theory Discretisation

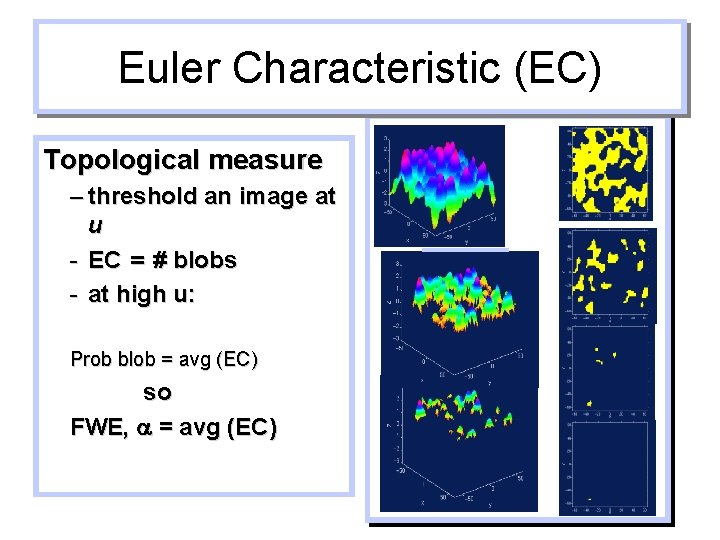
Euler Characteristic (EC) Topological measure – threshold an image at u - EC = # blobs - at high u: Prob blob = avg (EC) so FWE, a = avg (EC)

Example – 2 D Gaussian images α = R (4 ln 2) (2π) -3/2 u exp (-u 2/2) Voxel-wise threshold, u Number of Resolution Elements (RESELS), R N=100 x 100 voxels, Smoothness FWHM=10, gives R=10 x 10=100

Example – 2 D Gaussian images α = R (4 ln 2) (2π) -3/2 u exp (-u 2/2) For R=100 and α=0. 05 RFT gives u=3. 8

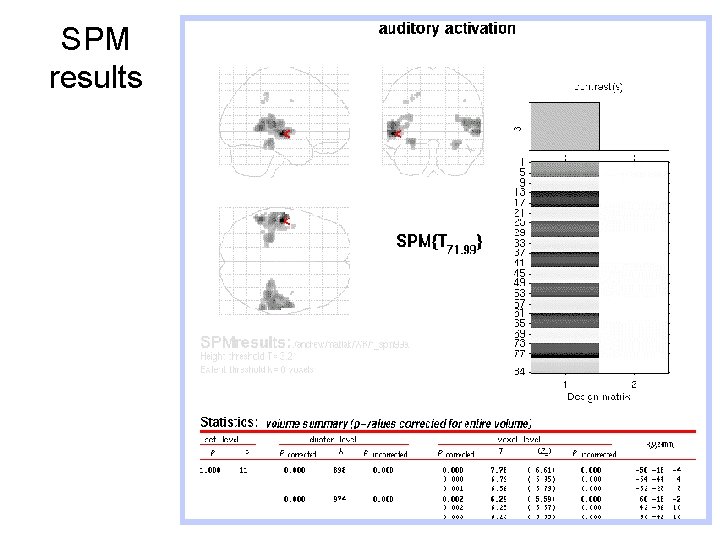
SPM results

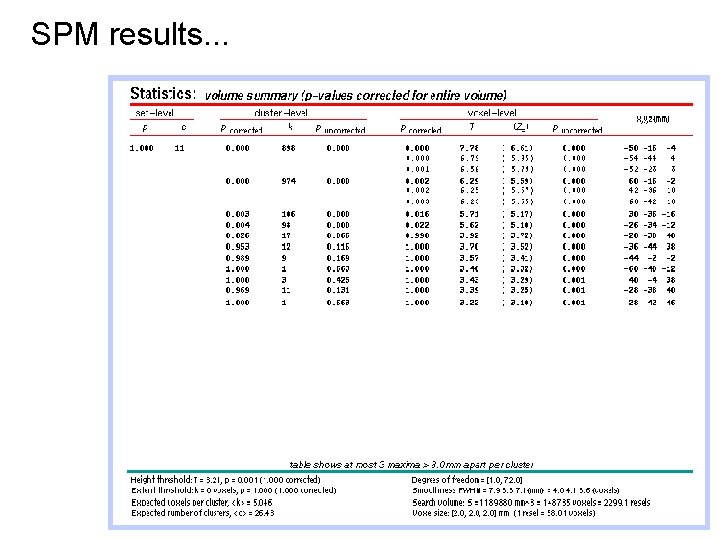
SPM results. . .

Outline • Voxel-wise General Linear Models • Random Field Theory • Bayesian Modelling

Motivation Even without applied spatial smoothing, activation maps (and maps of eg. AR coefficients) have spatial structure Contrast AR(1) We can increase the sensitivity of our inferences by smoothing data with Gaussian kernels (SPM 2). This is worthwhile, but crude. Can we do better with a spatial model (SPM 5) ? Aim: For SPM 5 to remove the need for spatial smoothing just as SPM 2 removed the need for temporal smoothing

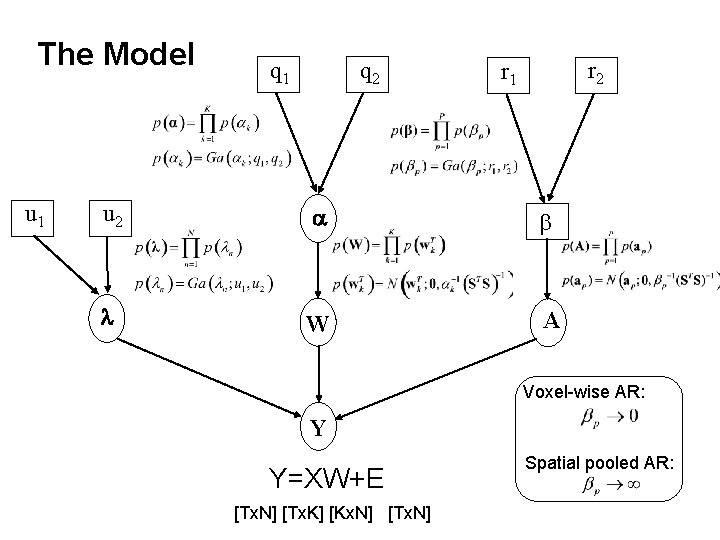
The Model u 1 q 2 r 1 u 2 a b l W A Voxel-wise AR: Y Y=XW+E [Tx. N] [Tx. K] [Kx. N] [Tx. N] Spatial pooled AR:

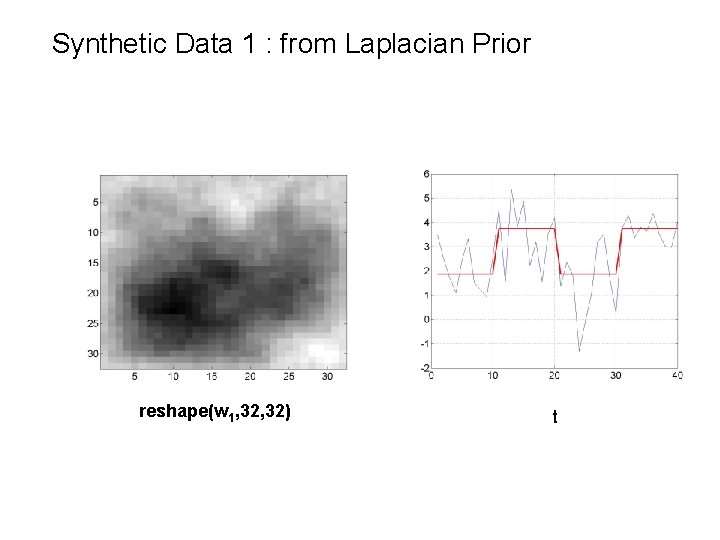
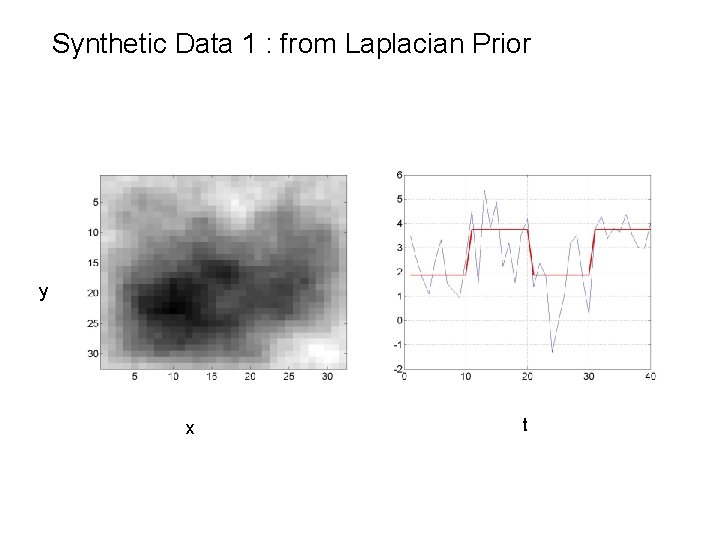
Synthetic Data 1 : from Laplacian Prior reshape(w 1, 32) t

Prior, Likelihood and Posterior In the prior, W factorises over k and A factorises over p: The likelihood factorises over n: The posterior over W therefore does’nt factor over k or n. It is a Gaussian with an NK-by-NK full covariance matrix. This is unwieldy to even store, let alone invert ! So exact inference is intractable.

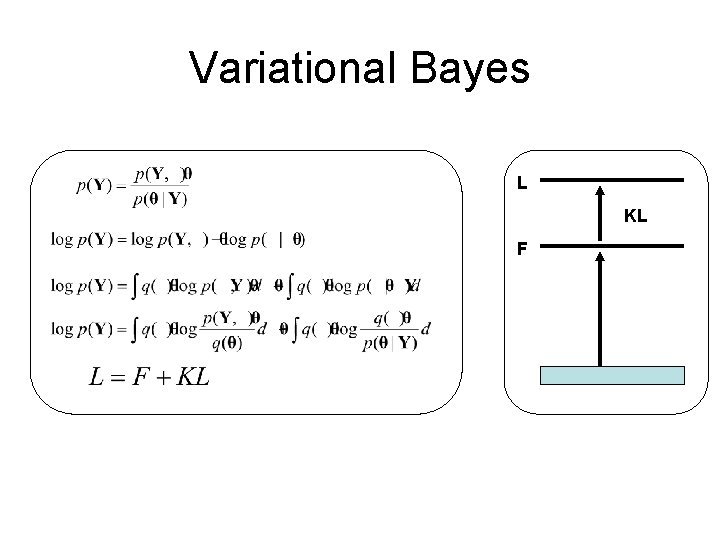
Variational Bayes L KL F

Variational Bayes If you assume posterior factorises then F can be maximised by letting where

Variational Bayes In the prior, W factorises over k and A factorises over p: In chosen approximate posterior, W and A factorise over n: So, in the posterior for W we only have to store and invert N K-by-K covariance matrices.

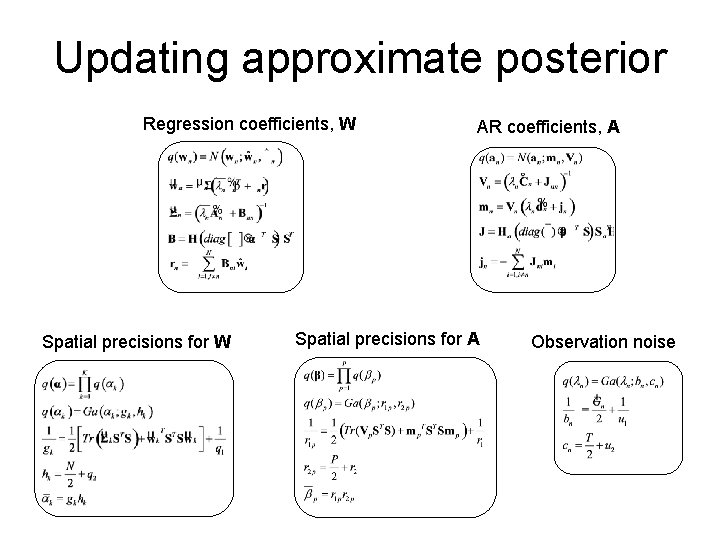
Updating approximate posterior Regression coefficients, W Spatial precisions for W AR coefficients, A Spatial precisions for A Observation noise

Synthetic Data 1 : from Laplacian Prior y x t

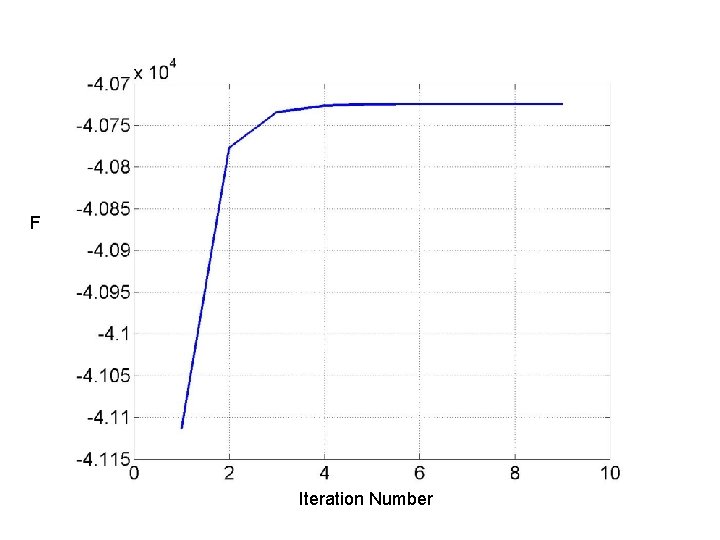
F Iteration Number

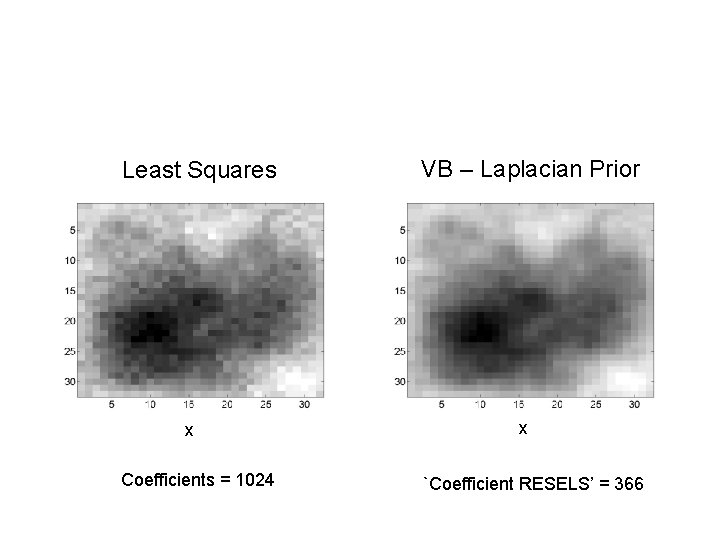
VB – Laplacian Prior Least Squares y y x Coefficients = 1024 x `Coefficient RESELS’ = 366

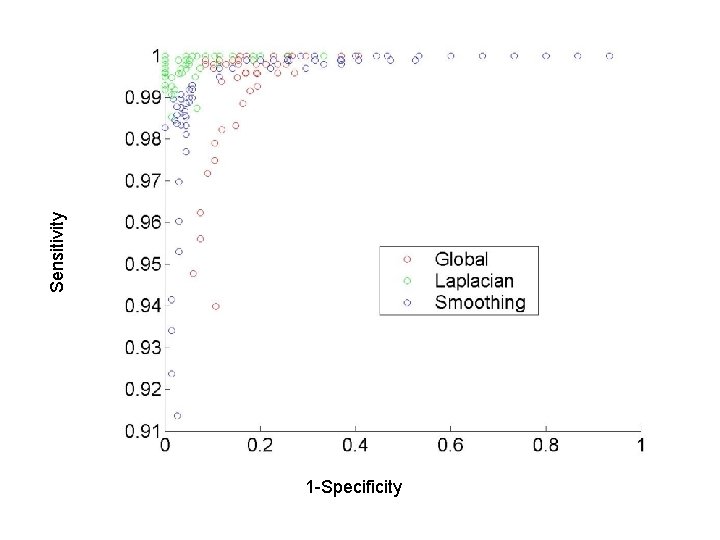
Synthetic Data II : blobs True Global prior Smoothing Laplacian prior

Sensitivity 1 -Specificity

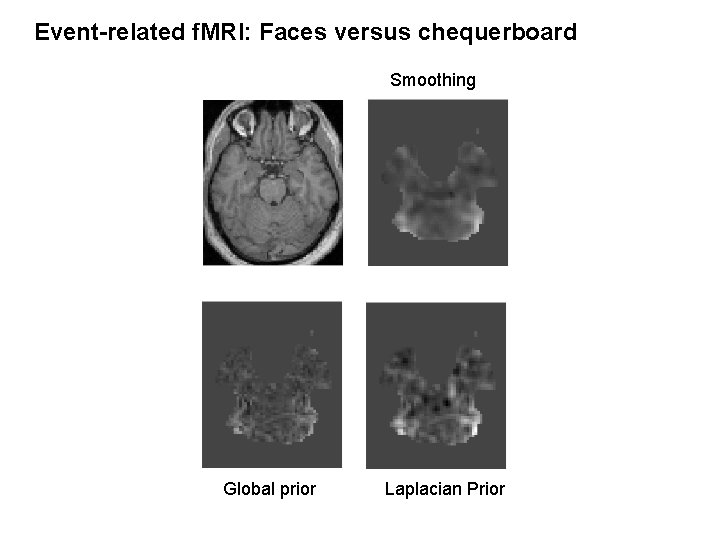
Event-related f. MRI: Faces versus chequerboard Smoothing Global prior Laplacian Prior

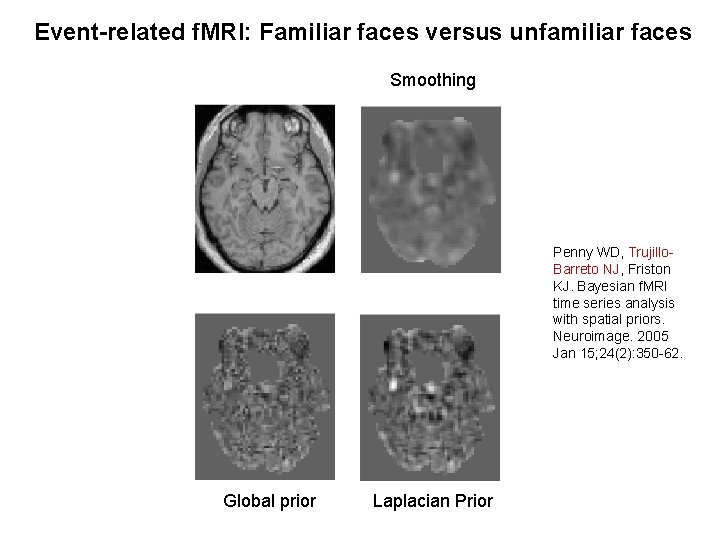
Event-related f. MRI: Familiar faces versus unfamiliar faces Smoothing Penny WD, Trujillo. Barreto NJ, Friston KJ. Bayesian f. MRI time series analysis with spatial priors. Neuroimage. 2005 Jan 15; 24(2): 350 -62. Global prior Laplacian Prior

Summary • Voxel-wise General Linear Models • Random Field Theory • Bayesian Modelling http: //www. fil. ion. ucl. ac. uk/~wpenny/mbi/index. html Graph-partitioned spatial priors for functional magnetic resonance images. Harrison LM, Penny W, Flandin G, Ruff CC, Weiskopf N, Friston KJ. Neuroimage. 2008 Dec; 43(4): 694 -707.