Statistical Parametric Mapping Lecture 11 Chapter 13 Head

Statistical Parametric Mapping Lecture 11 - Chapter 13 Head motion and correction Textbook: Functional MRI an introduction to methods, Peter Jezzard, Paul Matthews, and Stephen Smith Many thanks to those that share their MRI slides online

http: //www. fmrib. ox. ac. uk/fsl/

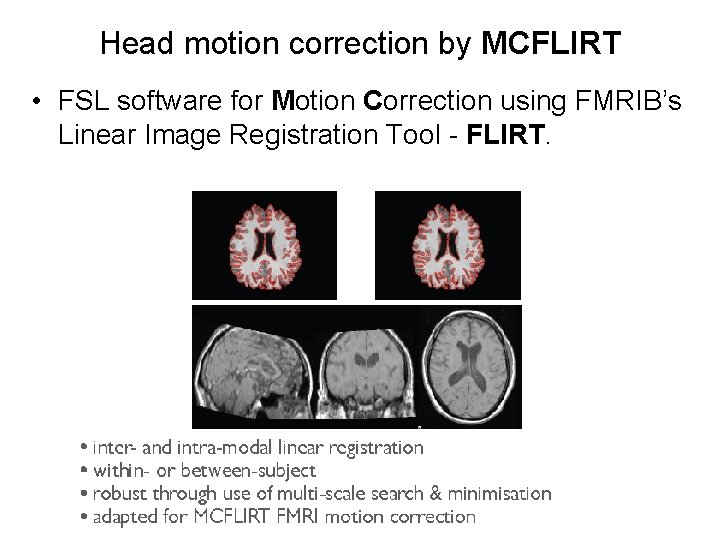
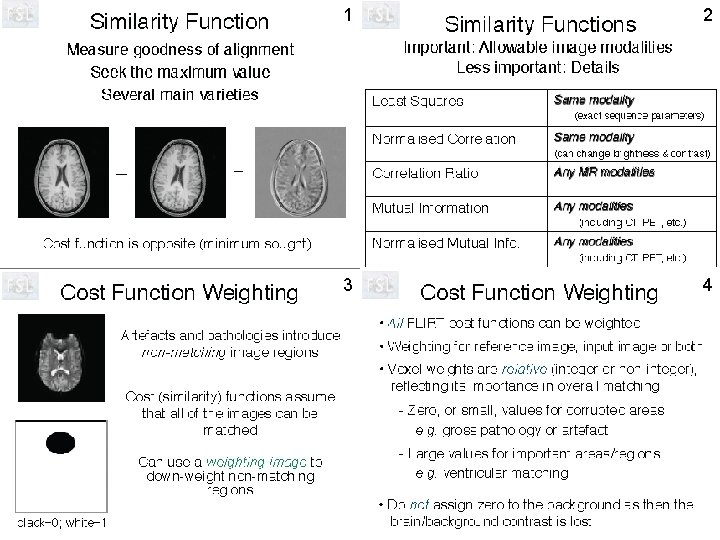
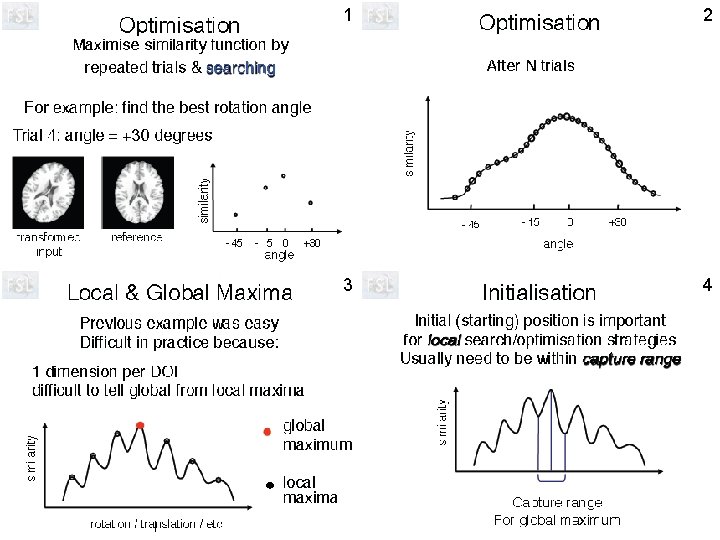
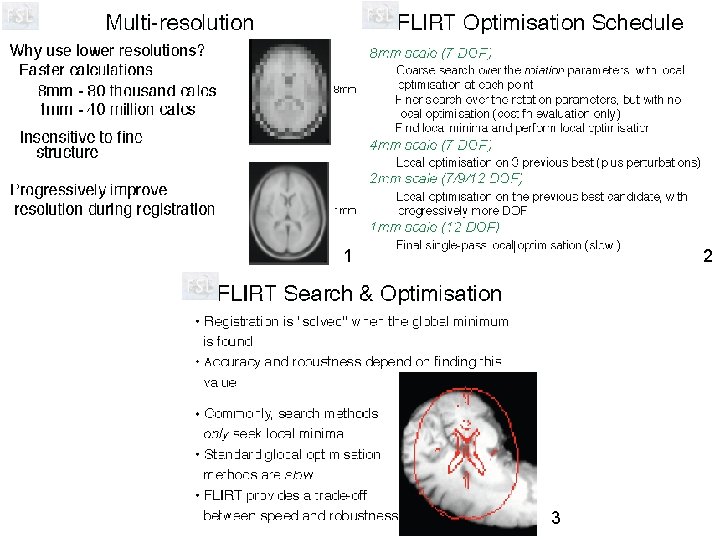
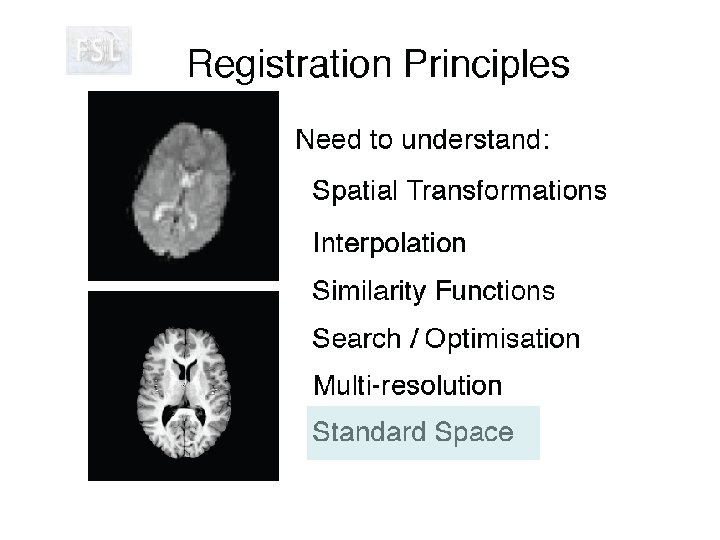
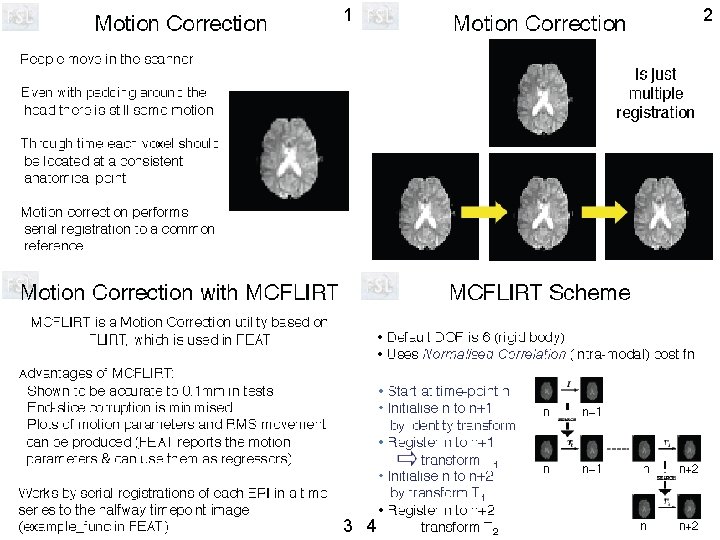
Head motion correction by MCFLIRT • FSL software for Motion Correction using FMRIB’s Linear Image Registration Tool - FLIRT.

1 2 3 4

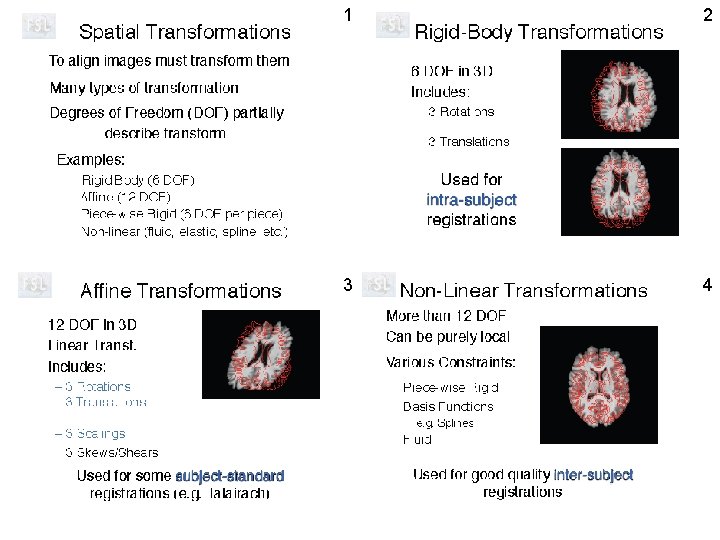
4 x 4 Affine transform matrix used with 3 -D images 3 each rotations, scales, shears m 14, m 24, and m 34 are x, y, and z translations Let R represent (x, y, z) column vectors and M the 4 x 4 transform matrix R’ = M R when you want to calculate primed location from unprimed one R = M-1 R’ when you want to calculate unprimed location from primed one

4 x 4 translation matrix T (3 parameters) M= [S][Rx][Ry][Rz][T] 4 x 4 scale matrix S (3 parameters) rotation matrix Rx for rotation about x-axis (1 parameter) rotation matrix Ry for rotation about y-axis (1 parameter) rotation matrix Rz for rotation about z-axis (1 parameter) Order of matrices important. Above ordering does translations first to match origins, then rotations about new origin, and finally scaling of the aligned image. For MC of f. MRI no scale, i. e. use only 3 translation and 3 rotation parameters.

1 2 3 4

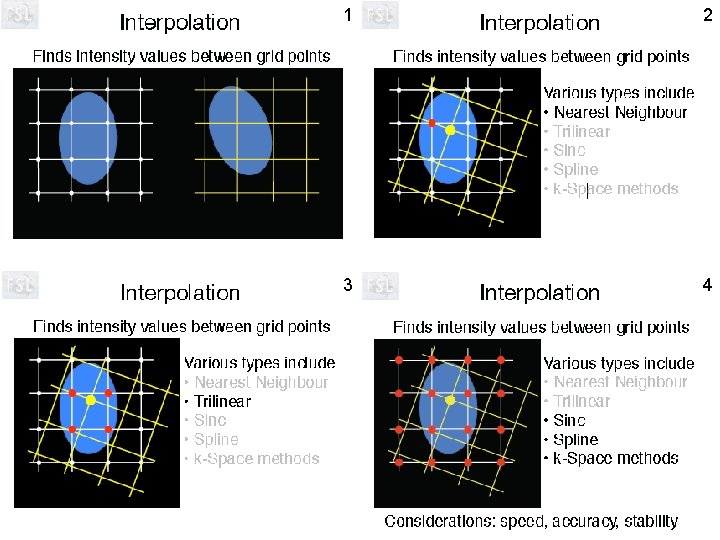
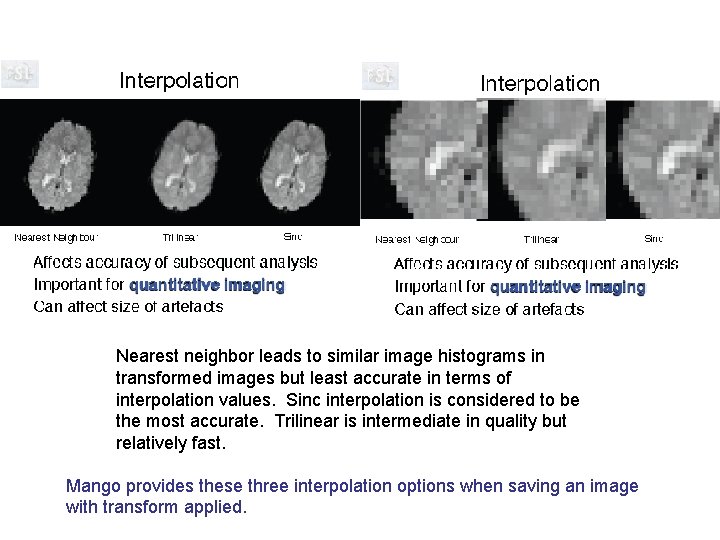
Nearest neighbor leads to similar image histograms in transformed images but least accurate in terms of interpolation values. Sinc interpolation is considered to be the most accurate. Trilinear is intermediate in quality but relatively fast. Mango provides these three interpolation options when saving an image with transform applied.

1 2 3 4

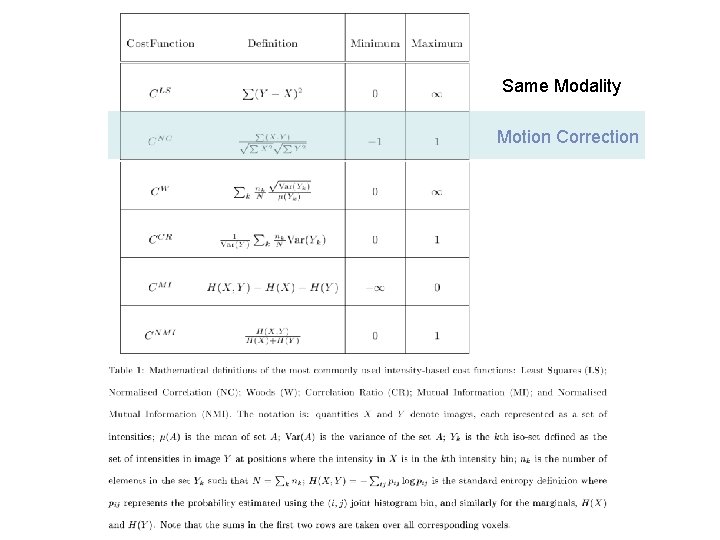
Same Modality Motion Correction

1 2 3 4

1 2 3

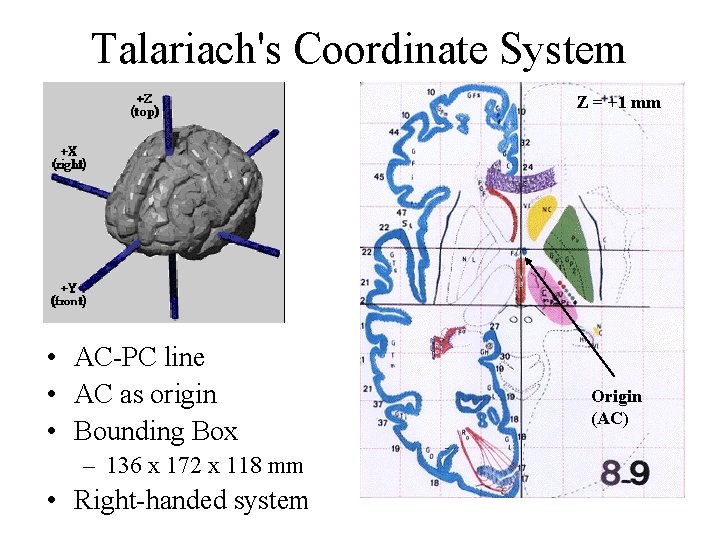
Talariach's Coordinate System Z = +1 mm • AC-PC line • AC as origin • Bounding Box – 136 x 172 x 118 mm • Right-handed system Origin (AC)

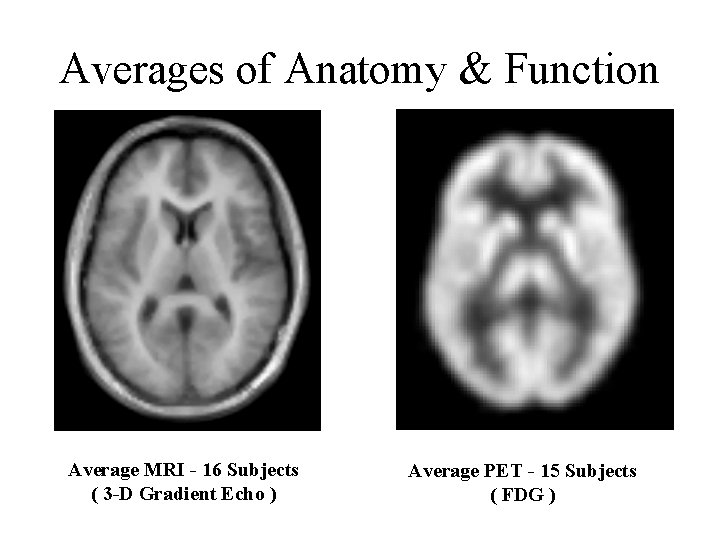
Averages of Anatomy & Function Average MRI - 16 Subjects ( 3 -D Gradient Echo ) Average PET - 15 Subjects ( FDG )

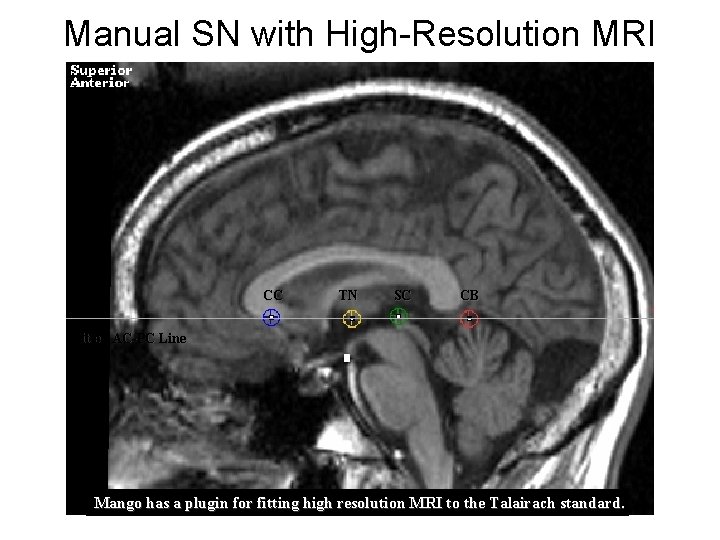
Manual SN with High-Resolution MRI CC TN SC CB Fitted AC-PC Line Mango has a plugin for fitting high resolution MRI to the Talairach standard.

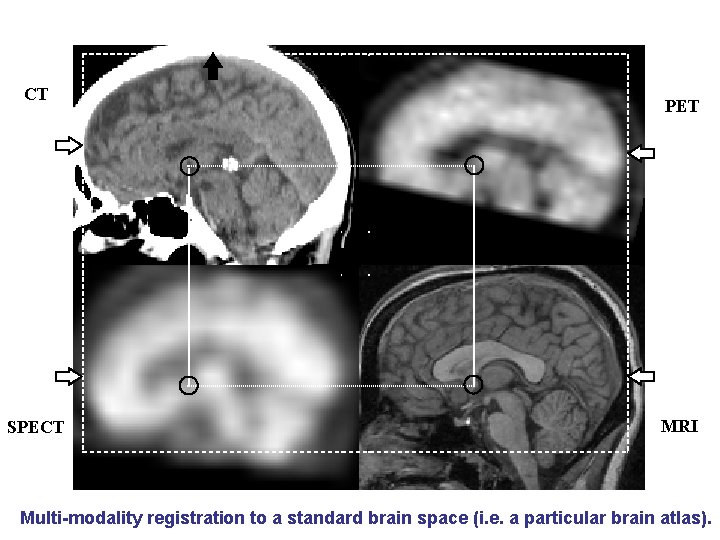
CT SPECT PET MRI Multi-modality registration to a standard brain space (i. e. a particular brain atlas).

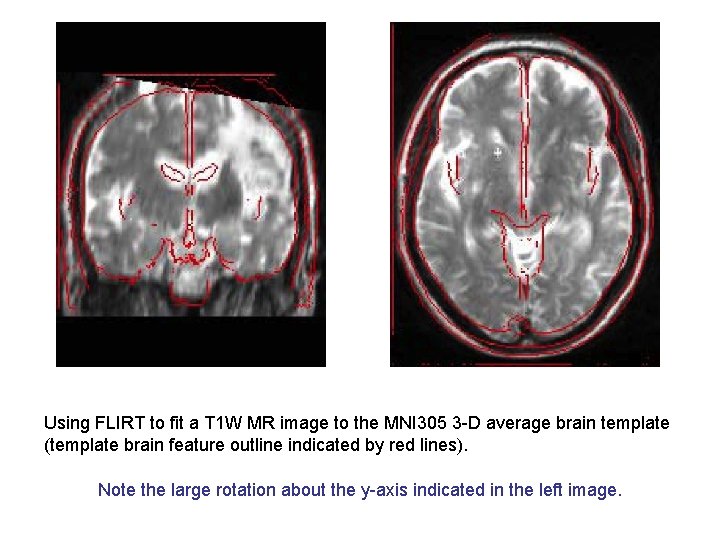
Using FLIRT to fit a T 1 W MR image to the MNI 305 3 -D average brain template (template brain feature outline indicated by red lines). Note the large rotation about the y-axis indicated in the left image.

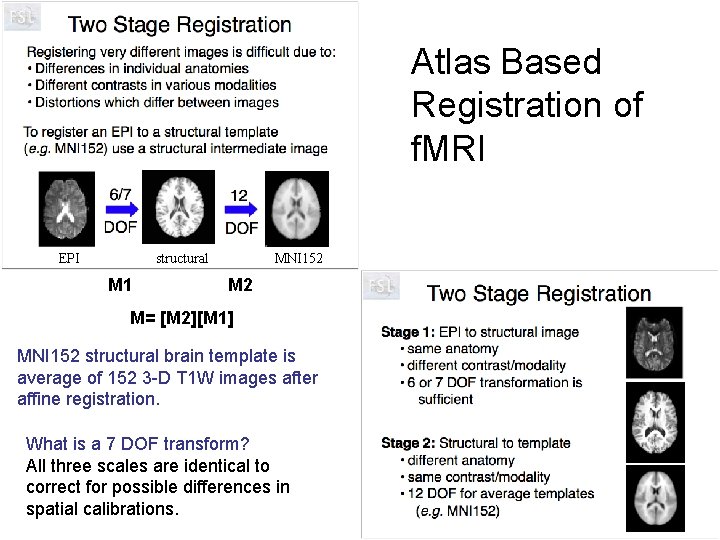
Atlas Based Registration of f. MRI EPI structural M 1 MNI 152 M 2 M= [M 2][M 1] MNI 152 structural brain template is average of 152 3 -D T 1 W images after affine registration. What is a 7 DOF transform? All three scales are identical to correct for possible differences in spatial calibrations.

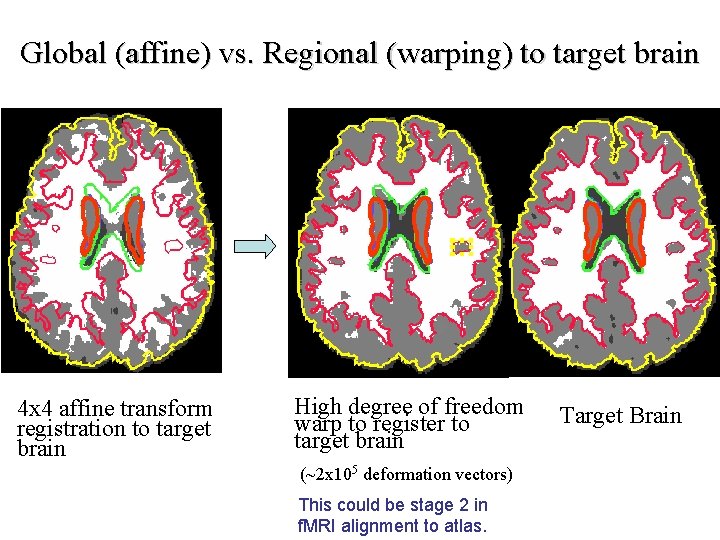
Global (affine) vs. Regional (warping) to target brain 4 x 4 affine transform registration to target brain High degree of freedom warp to register to target brain (~2 x 105 deformation vectors) This could be stage 2 in f. MRI alignment to atlas. Target Brain

1 3 4 2

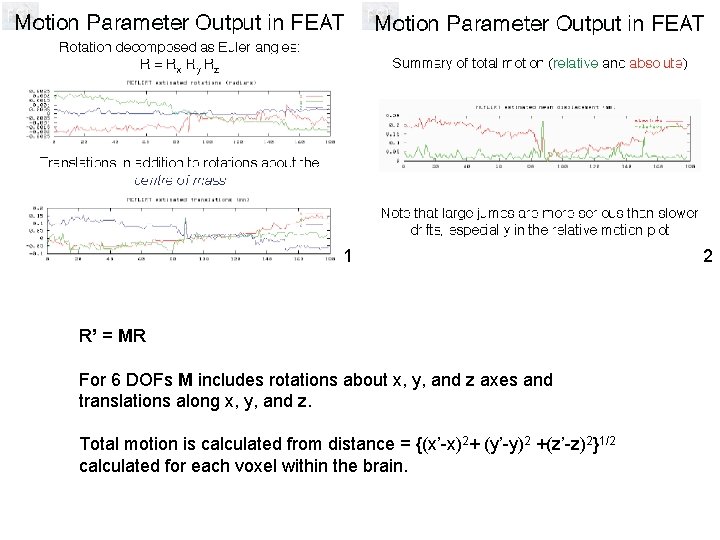
1 R’ = MR For 6 DOFs M includes rotations about x, y, and z axes and translations along x, y, and z. Total motion is calculated from distance = {(x’-x)2+ (y’-y)2 +(z’-z)2}1/2 calculated for each voxel within the brain. 2

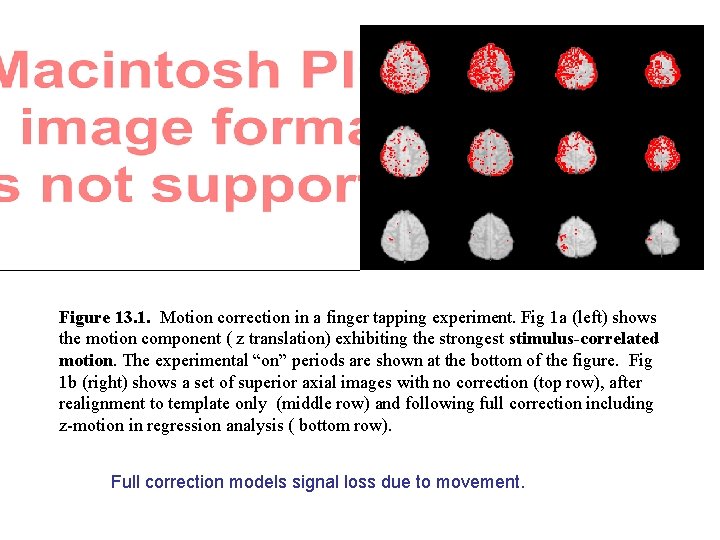
Figure 13. 1. Motion correction in a finger tapping experiment. Fig 1 a (left) shows the motion component ( z translation) exhibiting the strongest stimulus-correlated motion. The experimental “on” periods are shown at the bottom of the figure. Fig 1 b (right) shows a set of superior axial images with no correction (top row), after realignment to template only (middle row) and following full correction including z-motion in regression analysis ( bottom row). Full correction models signal loss due to movement.

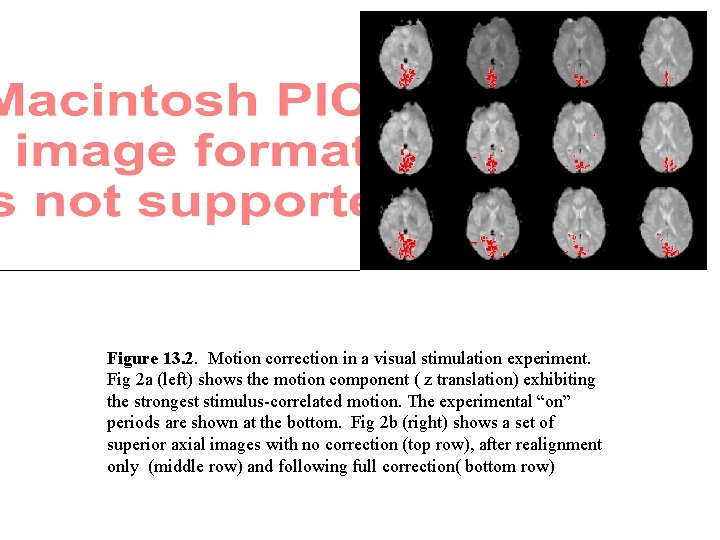
Figure 13. 2. Motion correction in a visual stimulation experiment. Fig 2 a (left) shows the motion component ( z translation) exhibiting the strongest stimulus-correlated motion. The experimental “on” periods are shown at the bottom. Fig 2 b (right) shows a set of superior axial images with no correction (top row), after realignment only (middle row) and following full correction( bottom row)

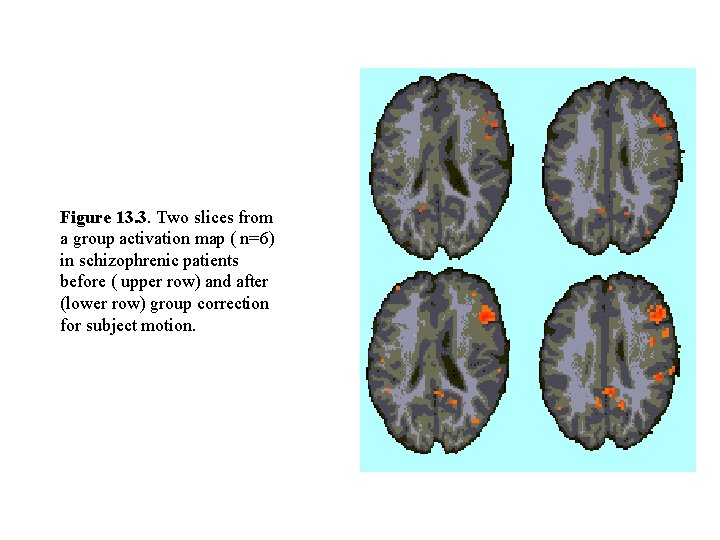
Figure 13. 3. Two slices from a group activation map ( n=6) in schizophrenic patients before ( upper row) and after (lower row) group correction for subject motion.

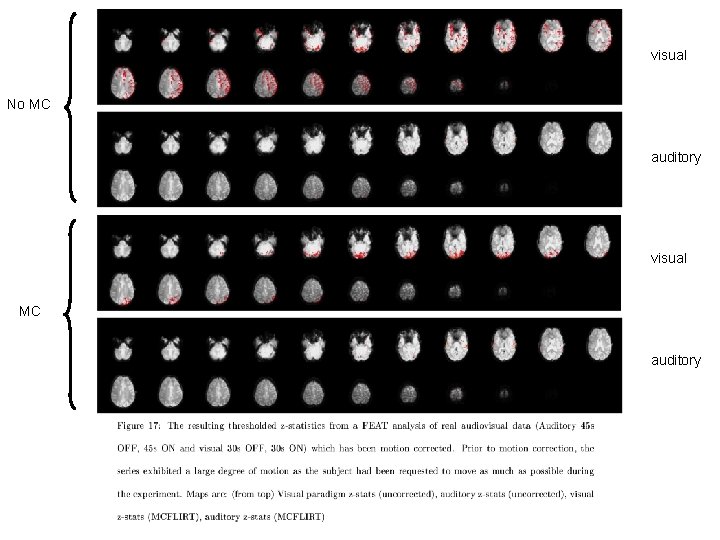
visual No MC auditory visual MC auditory

http: //www. fmrib. ox. ac. uk/fsl/