Statistical Methods to Prioritize GWAS Results by Integrating

Statistical Methods to Prioritize GWAS Results by Integrating Pleiotropy and Annotation Hongyu Zhao Yale School of Public Health June 25, 2014 Joint work with Min Chen, Lin Hou, Tianzhou Ma, Can Yang, Dong-Jun Chung, Cong Li, Judy Cho, Joel Gelernter

What we have learned from GWAS • Genes/Variants associated with phenotypes • Genetic risk prediction • Genetic architecture

What we have learned from GWAS • Genes/Variants associated with phenotypes • Prediction • Genetic architecture

Crohn’s Disease




![Network-Based Analysis • Start from a known interaction/co-expression network [N: assumed to be known] Network-Based Analysis • Start from a known interaction/co-expression network [N: assumed to be known]](http://slidetodoc.com/presentation_image/421b857d1165826516a2f2454b6246a3/image-9.jpg)
Network-Based Analysis • Start from a known interaction/co-expression network [N: assumed to be known] • Each gene is either associated or not associated with a phenotype [D: unknown] • Each gene has an observed statistical evidence for association [Z: observed] • Goal: Infer D conditional on N and Z Chen, Cho, Zhao (2011) PLo. S Genetics

Chen, Cho, Zhao (2011) PLo. S Genetics
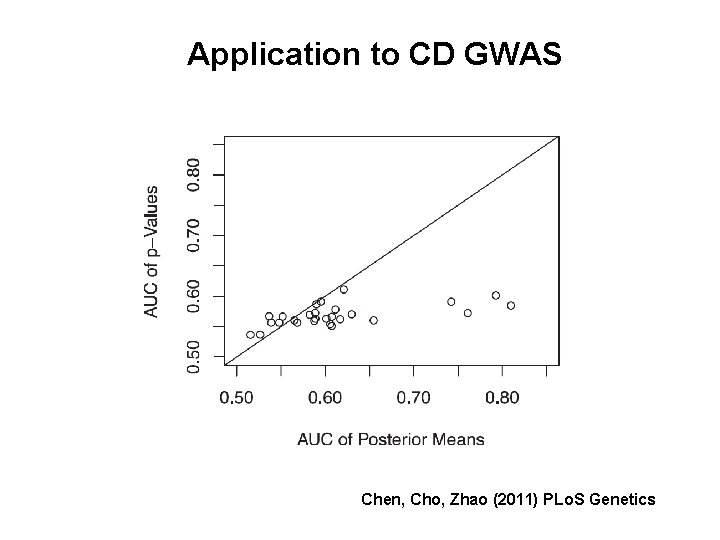
Application to CD GWAS Chen, Cho, Zhao (2011) PLo. S Genetics
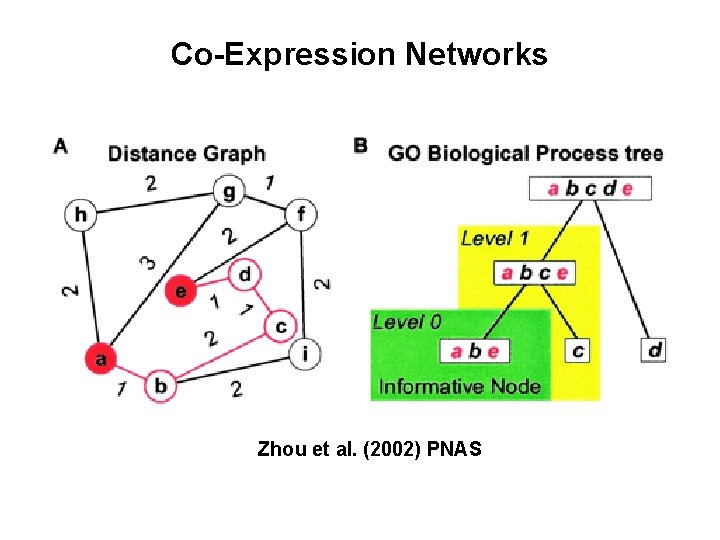
Co-Expression Networks Zhou et al. (2002) PNAS
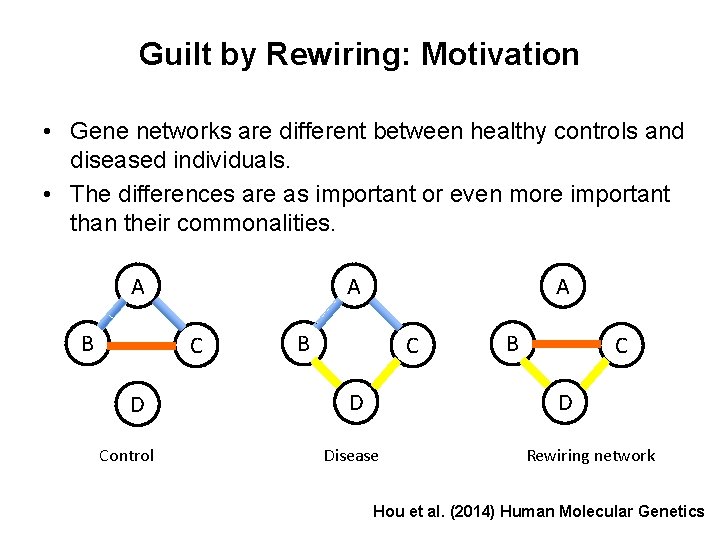
Guilt by Rewiring: Motivation • Gene networks are different between healthy controls and diseased individuals. • The differences are as important or even more important than their commonalities. A B A C D Control A B C D Disease Rewiring network Hou et al. (2014) Human Molecular Genetics
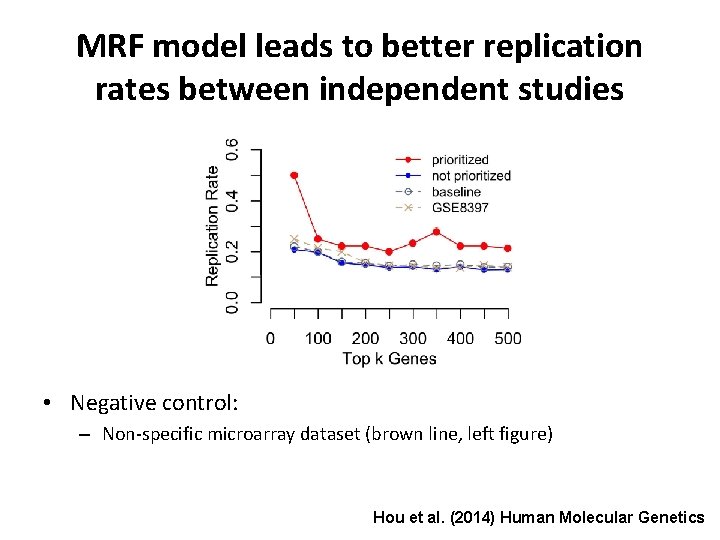
MRF model leads to better replication rates between independent studies • Negative control: – Non-specific microarray dataset (brown line, left figure) Hou et al. (2014) Human Molecular Genetics


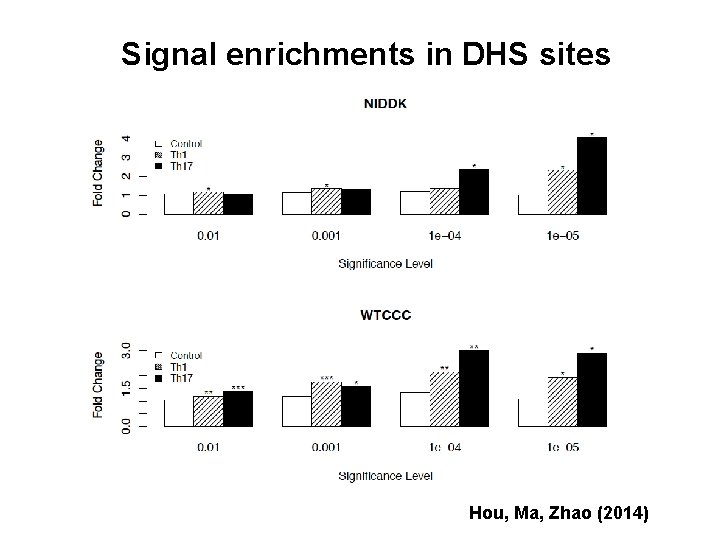
Signal enrichments in DHS sites Hou, Ma, Zhao (2014)
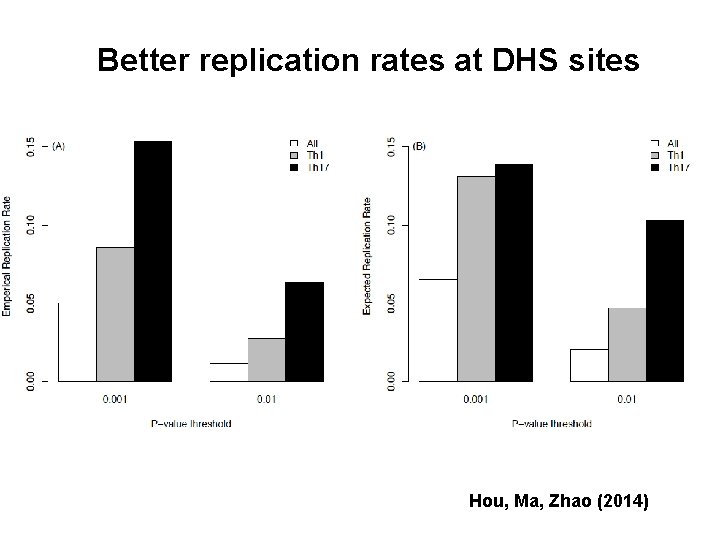
Better replication rates at DHS sites Hou, Ma, Zhao (2014)
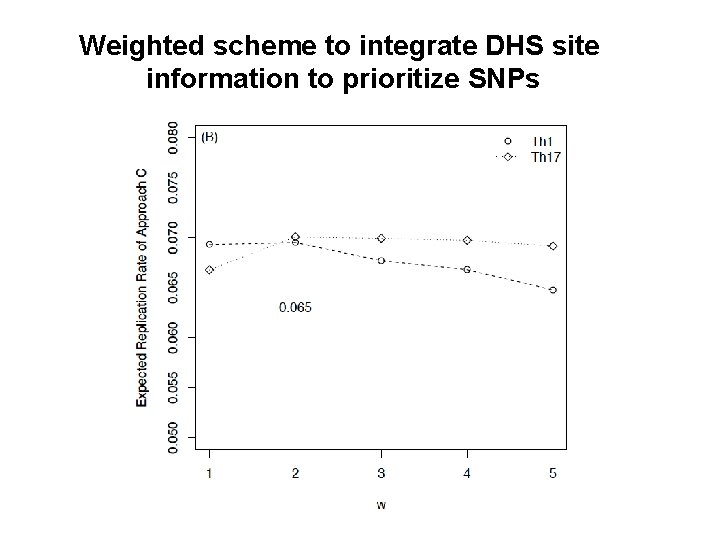
Weighted scheme to integrate DHS site information to prioritize SNPs
http: //dongjunchung. github. io/GPA/
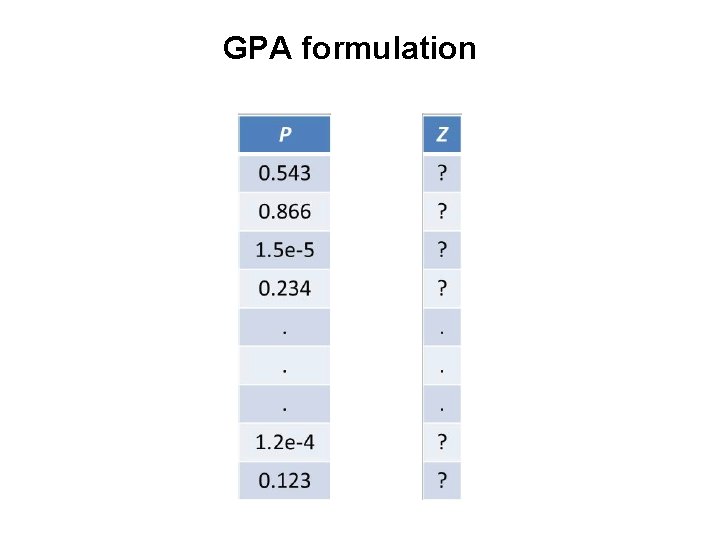
GPA formulation
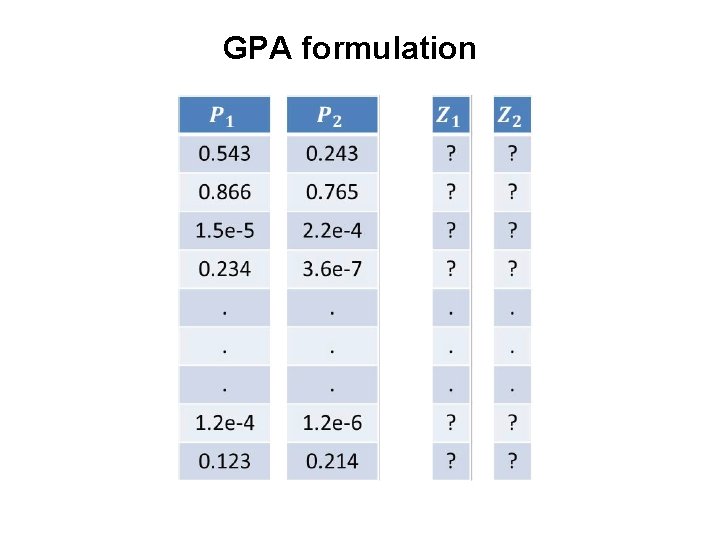
GPA formulation

GPA formulation
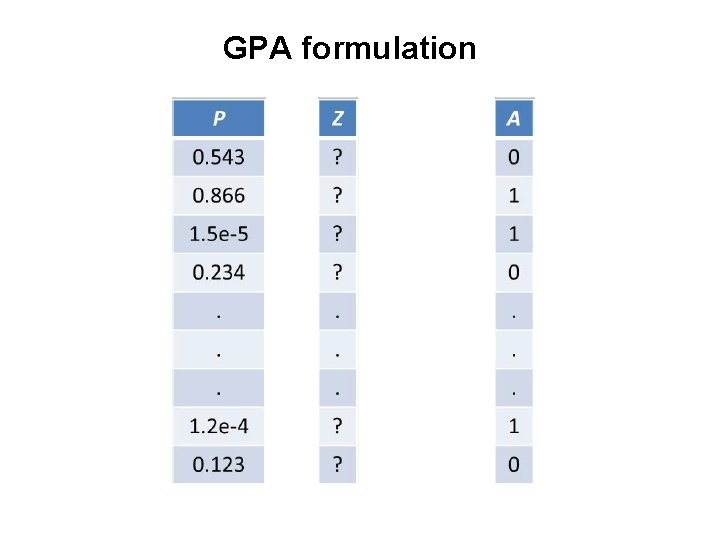
GPA formulation
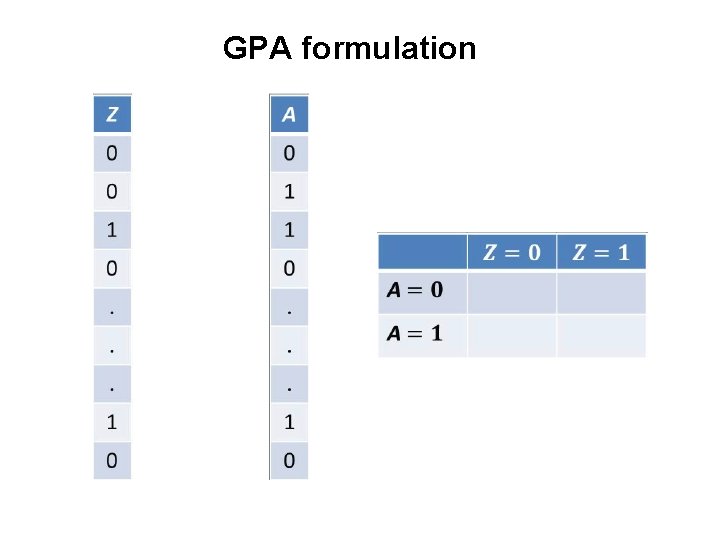
GPA formulation
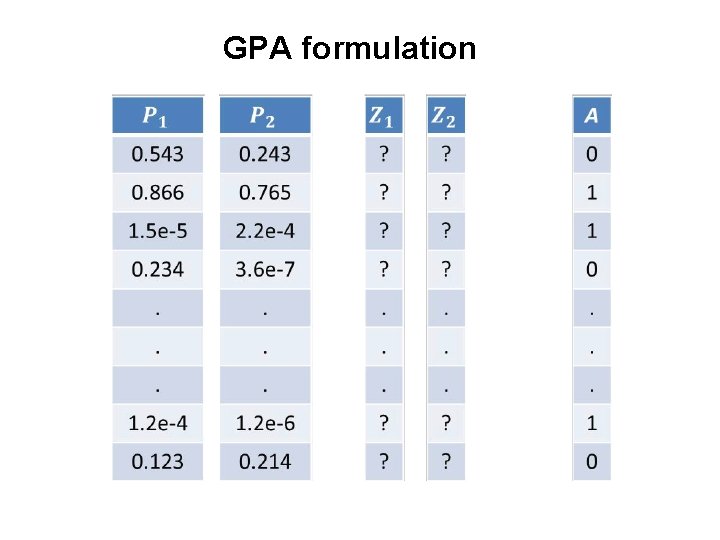
GPA formulation
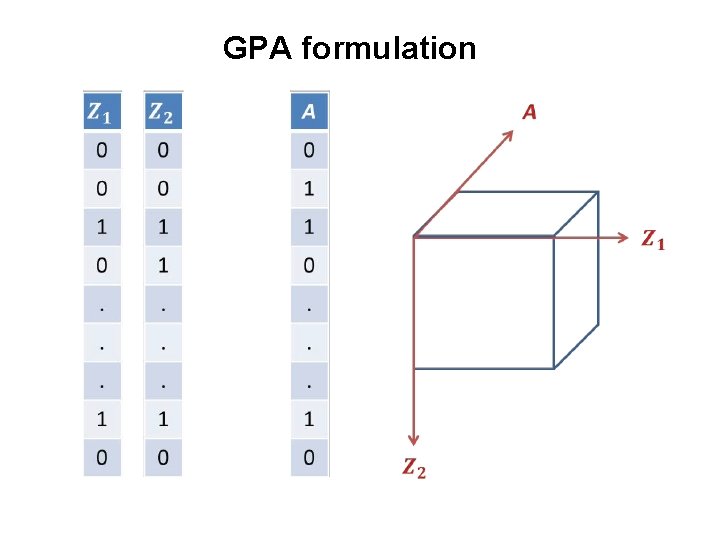
GPA formulation

GPA: Single GWAS Chung et al. (2014) PLo. S Genetics, under revision

GPA: Modeling Pleiotropy

GPA: Modeling Annotation Data

Modeling Pleiotropy and Annotation

Key Assumptions for GPA

Simulations

Comparisons with conditional FDR approach

GPA: Enrichment Testing • Pleiotropy & enrichment for annotation can be checked conveniently using the hypothesis testing procedure incorporated into the GPA G 1/G 2 Null Assoc. framework. Null Assoc. • Null hypothesis for pleiotropy: H 0: ( π10 + π11 ) ( π01 + π11 ) = π11 π00 π01 π10 π11 • Hypothesis testing for annotation enrichment: H 0: q 0 = q 1

GPA: Hypothesis Testing

Comparisons with GSEA

Five Psychiatric Disorders • Five psychiatric disorders: – – – ADHD. Autism spectrum disorder. Bipolar disorder. Major depression disorder. Schizophrenia. • Strong pleiotropy exists for BIP-SCZ, MDD-SCZ, ASD-SCZ, & BIP-MDD.

Five Psychiatric Disorders BIP: separate analysis BIP: joint analysis

Five Psychiatric Disorders SCZ: separate analysis SCZ: joint analysis

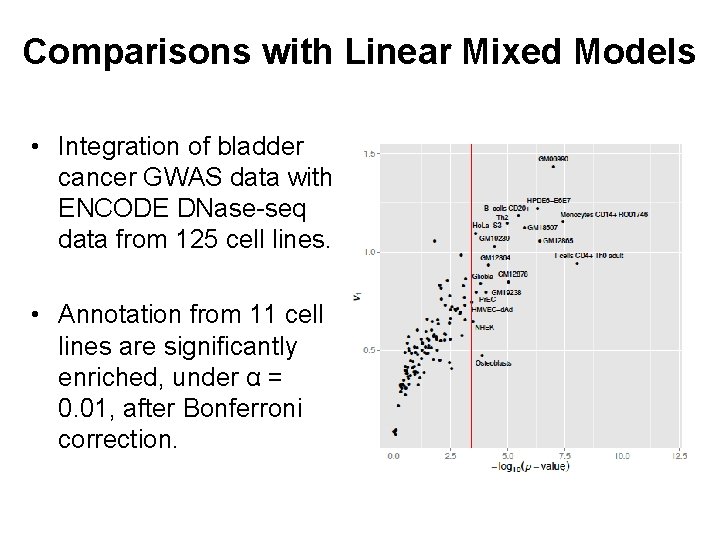
Comparisons with Linear Mixed Models • Integration of bladder cancer GWAS data with ENCODE DNase-seq data from 125 cell lines. • Annotation from 11 cell lines are significantly enriched, under α = 0. 01, after Bonferroni correction.

Acknowledgements Medicine: Judy Cho (Mount Sinai) Psychiatry: Joel Gelernter Yale Center for Statistical Genomics and Proteomics: Min Chen (UT Dallas), Lin Hou, Tianzhou Ma (U. Pittsburgh), Can Yang (HKBU), Dong-Jun Chung (MUSC), Cong Li Various NIH and NSF grants
- Slides: 43