Statistical Mechanics and Soft Condensed Matter Fluctuating membranes

Statistical Mechanics and Soft Condensed Matter Fluctuating membranes by Pietro Cicuta

Slide 1: The thermally driven roughness of membranes can be analysed statistically. Reprinted with permission from Dr Markus Deserno, Carnegie Mellon University

Position vector: s = (x, y, h (x, y)) Tangent vectors along x and y: where Plane tangent to the surface at (x, y, h (x, y)): Slide 2: Monge representation of a deformed membrane.

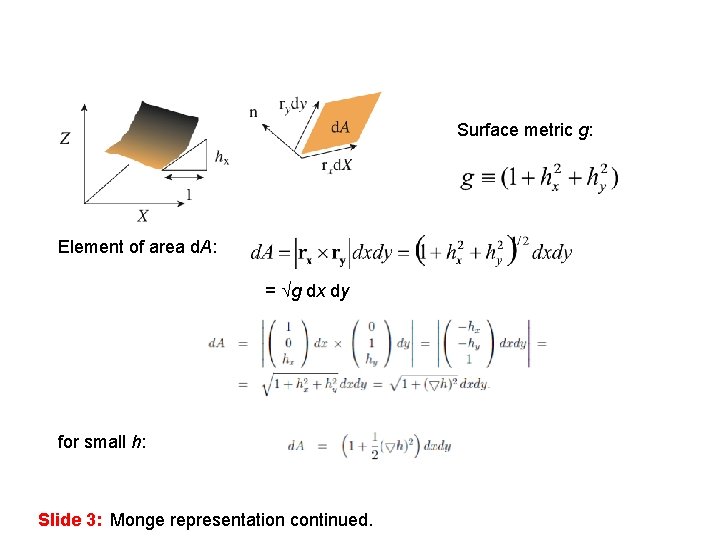
Surface metric g: Element of area d. A: = g dx dy for small h: Slide 3: Monge representation continued.

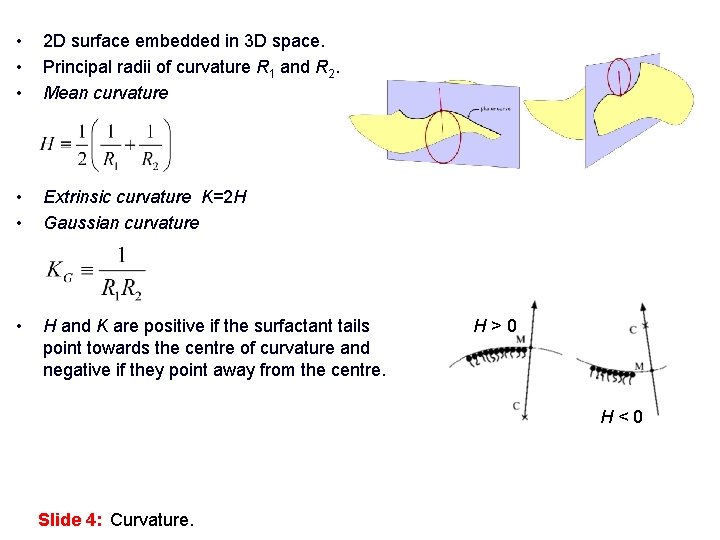
• • • 2 D surface embedded in 3 D space. Principal radii of curvature R 1 and R 2. Mean curvature • • Extrinsic curvature K=2 H Gaussian curvature • H and K are positive if the surfactant tails point towards the centre of curvature and negative if they point away from the centre. H>0 H<0 Slide 4: Curvature.

Curvature where s is the arc length In one dimension: Non-trivial extension to two dimensions: Slide 5: Curvature of membranes.

K = 2 H • Work δE required to deform the membrane against tension and bending: Slide 6: Curvature and energy.

The function h (x, y) can be decomposed into discrete Fourier modes or written in terms of its Fourier transform: Substituting into the expression for the fluctuation energy, we get: Slide 7: Fourier transform.

• Integrating over dx and dy generates a delta function, hence a simplified equation: • From equipartition of energy: • Spectrum for the mean square amplitude of fluctuations: Note the strong dependence on q, particularly in connection with the bending modulus. Slide 8: Fluctuation spectrum.

Mean amplitude: qmin = 2π/L qmax = 2π/d Typically, bending stiffness is hence Slide 9: Mean amplitude of fluctuations. d ~ bilayer thickness