Statistical Machine Learning in Markov Random Fields Kazuyuki

マルコフ確率場によるデータからの統計的機械学習モデリング Statistical Machine Learning in Markov Random Fields 田中和之 東北大学大学院情報科学研究科 Kazuyuki Tanaka GSIS, Tohoku University, Sendai, Japan http: //www. smapip. is. tohoku. ac. jp/~kazu/ Collaborators Muneki Yasuda (Yamagata University, Japan) Masayuki Ohzeki (Tohoku University, Japan) Shun Kataoka (Tohoku University, Japan) Yuya Seki (Tohoku University, Japan) Candy Hsu (National Tsin Hua University, Taiwan) Mike Titterington (University of Glasgow, UK) January, 2017 Math. AM-OIL Workshop 1

Outline 1. 2. 3. 4. 5. 6. 7. 8. Introduction Statistical Machine Learning in Markov Random Fields Generalized Sparse Prior for Image Modeling Probabilistic Noise Reduction Probabilistic Image Segmentation Statistical Machine Learning by Inverse Renormalization Group Transformation Related Works Concluding Remarks January, 2017 Math. AM-OIL Workshop 3

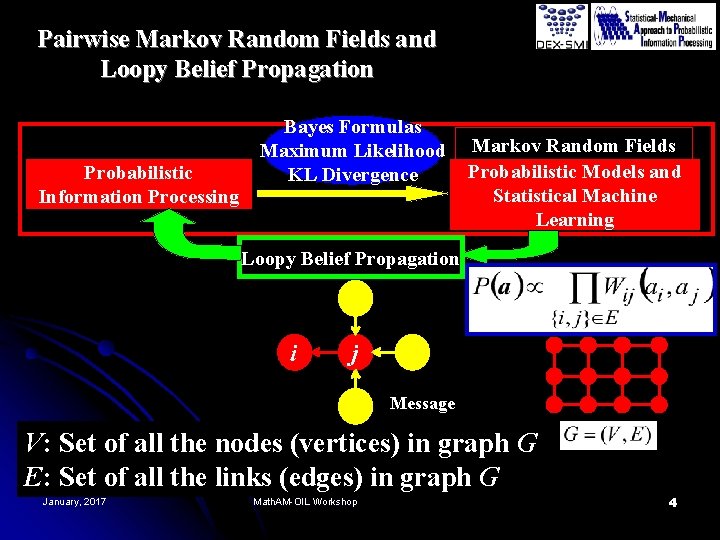
Pairwise Markov Random Fields and Loopy Belief Propagation Probabilistic Information Processing Bayes Formulas Maximum Likelihood KL Divergence Markov Random Fields Probabilistic Models and Statistical Machine Learning Loopy Belief Propagation i j Message V: Set of all the nodes (vertices) in graph G E: Set of all the links (edges) in graph G January, 2017 Math. AM-OIL Workshop 4

Supervised Learning of Pairwise Markov Random Fields Pairwise MRF 1 2 3 4 5 6 7 8 9 10 11 12 Maximization of Marginal Likelihood V: Set of all the nodes (vertices) January, 2017 Math. AM-OIL Workshop E: Set of all the links (edges) 5

Pairwise Markov Random Fields for Bayesian Image Modeling In Bayesian image modeling, natural images are often assumed to be generated by according to the following pairwise Markov random fields: Hamiltonian of Classical Spin System January, 2017 Math. AM-OIL Workshop 6

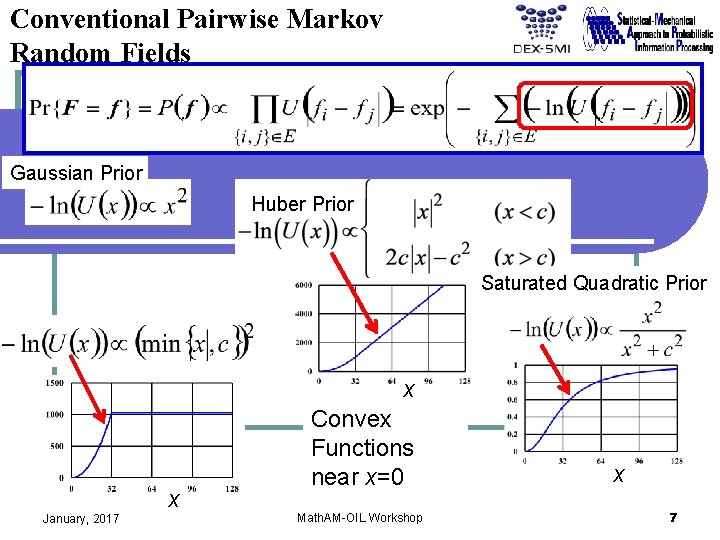
Conventional Pairwise Markov Random Fields Gaussian Prior Huber Prior Saturated Quadratic Prior x January, 2017 x Convex Functions near x=0 Math. AM-OIL Workshop x 7

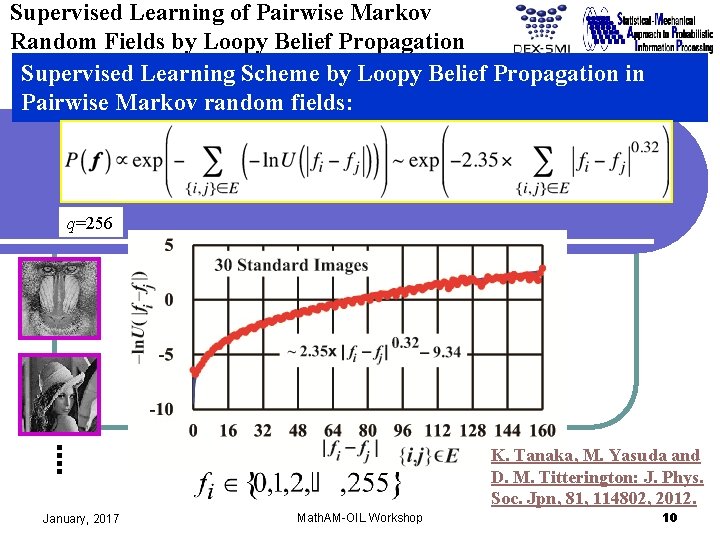
Supervised Learning of Pairwise Markov Random Fields Supervised Learning Scheme by Loopy Belief Propagation in Pairwise Markov random fields: Supervised Learning 30 Standard Images January, 2017 Math. AM-OIL Workshop 8

Supervised Learning of Pairwise Markov Random Fields by Loopy Belief Propagation Supervised Learning Scheme by Loopy Belief Propagation in Pairwise Markov random fields: Histogram from Supervised Data M. Yasuda, S. Kataoka and K. Tanaka, J. Phys. Soc. Jpn, Vol. 81, No. 4, Article No. 044801, 2012. January, 2017 Math. AM-OIL Workshop 9

Supervised Learning of Pairwise Markov Random Fields by Loopy Belief Propagation Supervised Learning Scheme by Loopy Belief Propagation in Pairwise Markov random fields: q=256 K. Tanaka, M. Yasuda and D. M. Titterington: J. Phys. Soc. Jpn, 81, 114802, 2012. January, 2017 Math. AM-OIL Workshop 10

Bayesian Image Modeling by Generalized Sparse Prior Assumption: Prior Probability is given as the following Gibbs distribution with the interaction a between every nearest neighbour pair of pixels: p=0: Potts model p=2: Discrete Gaussian Graphical Model January, 2017 Math. AM-OIL Workshop 11

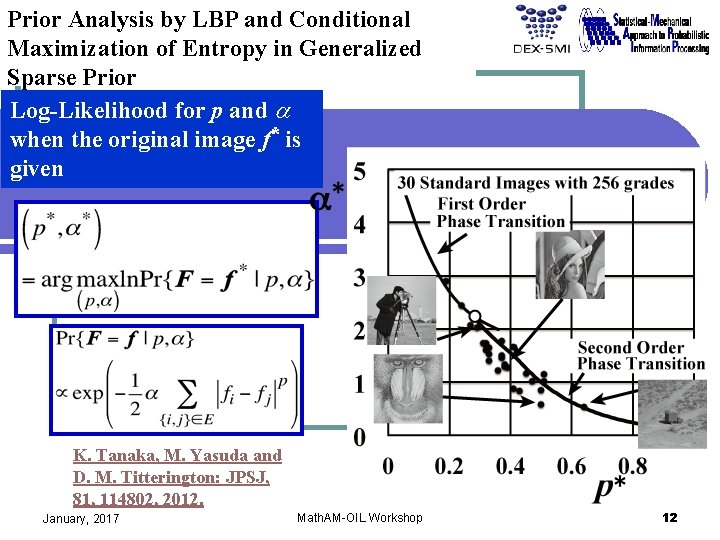
Prior Analysis by LBP and Conditional Maximization of Entropy in Generalized Sparse Prior Log-Likelihood for p and a when the original image f* is given K. Tanaka, M. Yasuda and D. M. Titterington: JPSJ, 81, 114802, 2012. January, 2017 Math. AM-OIL Workshop 12

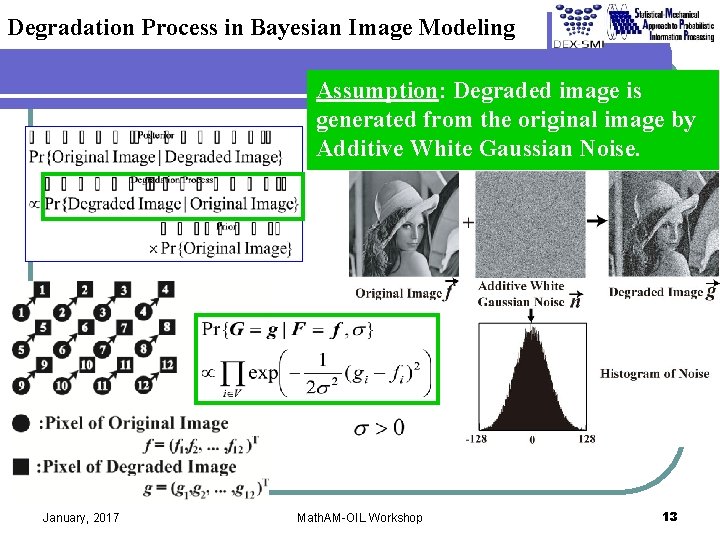
Degradation Process in Bayesian Image Modeling Assumption: Degraded image is generated from the original image by Additive White Gaussian Noise. January, 2017 Math. AM-OIL Workshop 13

Hyperparameter Estimation of Pairwise Markov Random Fields Data Generative Model Prior Probability Pairwise MRF Joint Probability Marginal Likelihood 5 9 2 3 4 5 6 7 8 9 10 11 12 2 1 Probability of Data d Likelihood of a and b 1 1 5 9 6 10 3 2 6 10 7 11 4 3 7 8 12 11 4 8 12 Maximization of Marginal Likelihood Expectation Maximization (EM) Algorithm V: Set of all the nodes (vertices) January, 2017 Math. AM-OIL Workshop E: Set of all the links (edges) 14

Noise Reductions by Generalized Sparse Priors and Loopy Belief Propagation Original Image K. Tanaka, M. Yasuda and D. M. Titterington: J. Phys. Soc. Jpn, 81, 114802, 2012. Degraded Image K. Tanaka, M. Yasuda and D. M. Titterington: JPSJ, 81, 114802, 2012. Restored Image p=0. 5 January, 2017 p=2. 0 Math. AM-OIL Workshop Continuous Gaussian Graphical Model p=2. 0 15

Bayesian Modeling for Image Segmentation using MRF Data Parameter ai = 0, 1, …, q-1 Segment image data into some regions using belief propagation and EM algorithm Posterior Probability Dstribution Potts Prior 12 q+1 Hyperparameters Data Generative Model Likelihood of Hyperparameter Maximization of Posterior Marginal (MPM) Berkeley Segmentation Data Set 500 (BSDS 500), http: //www. eecs. berkeley. edu/Research/Projects/CS/vision/grouping/ P. Arbelaez, M. Maire, C. Fowlkes and J. Malik: IEEE Trans. PAMI, 33, 898, Math. AM-OIL Workshop 2011. January, 2017 16

Bayesian Image Segmentation Intel® Core™ i 7 -4600 U CPU with a memory of 8 GB Potts Prior Hyperparameter q=8 321 x 481 Hyperparameter Estimation in Maximum Likelihood Framewrok and Maximization of Posterior Marginal (MPM) Estimation with Loopy Belief Propagation for Observed Color Image d K. Tanaka, S. Kataoka, M. Yasuda, Y. Waizumi and C. -T. Hsu: JPSJ, . 83, 124002, 2014. 481 x 321 January, 2017 Berkeley Segmentation Data Set 500 (BSDS 500), http: //www. eecs. berkeley. edu/Research/Projects/CS/vision/grouping/ P. Arbelaez, M. Maire, C. Fowlkes and J. Malik: IEEE Trans. PAMI, 33, 898, 2011. Math. AM-OIL Workshop 17

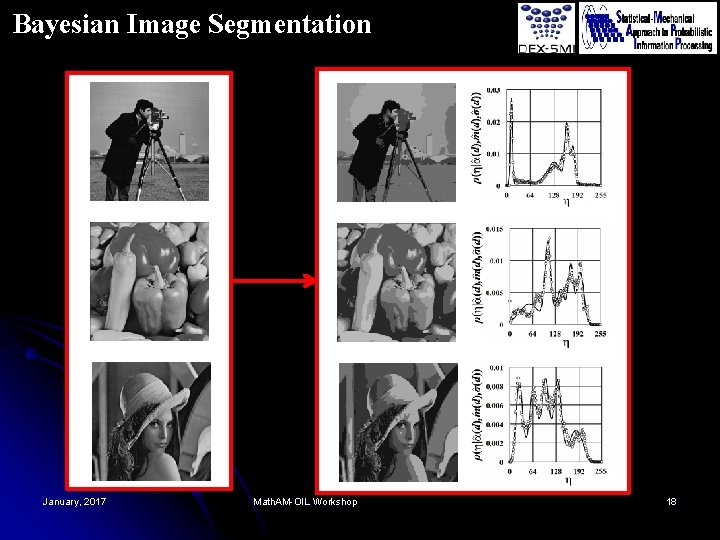
Bayesian Image Segmentation January, 2017 Math. AM-OIL Workshop 18

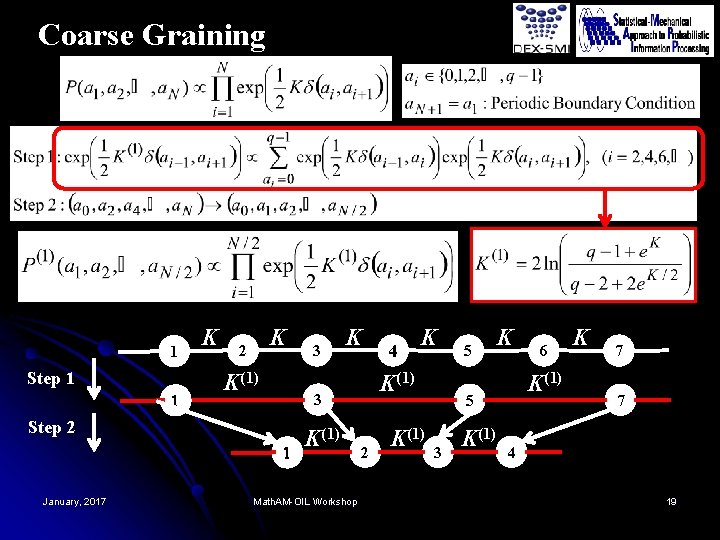
Coarse Graining 1 Step 1 1 K K 2 K(1) K 1 K(1) Math. AM-OIL Workshop 4 K K(1) 3 Step 2 January, 2017 3 2 K(1) 5 K K(1) 5 3 K(1) 6 K 7 7 4 19

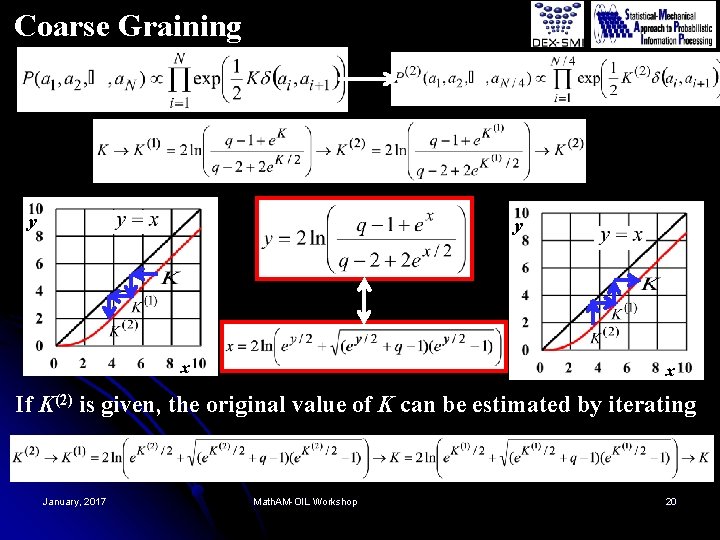
Coarse Graining y y x x x If K(2) is given, the original value of K can be estimated by iterating January, 2017 Math. AM-OIL Workshop 20

Coarse Graining q=8 January, 2017 Math. AM-OIL Workshop 21

Bayesian Image Segmentation Potts Prior Hyperparameter Estimation in Maximization of Marginal Likelihood with Belief Propagation for Original Image Hyperparameter Estimation in Maximization of Marginal Likelihood with Belief Propagation after Coarse Graining Procedures Segmentation by Belief Propagation for Original Image 20 x 30 321 x 481 January, 2017 Coarse Graining Procedures (r =8) 20 x 30 Labeled Image Math. AM-OIL Workshop 22

Bayesian Image Segmentation Potts Prior 481 x 321 Hyperparameter Estimation in Maximum Likelihood Framework with Belief Propagation for Original Image q=8 Hyperparameter Estimation in Maximum Likelihood Framework with Belief Propagation after Coarse Graining Procedures Intel® Core™ i 7 -4600 U CPU with a memory of 8 GB Segmentation by Belief Propagation for Original Image MPM with LBP 30 x 20 Coarse Graining Labeled Image Procedures (r =8) Berkeley Segmentation Data Set 500 (BSDS 500), http: //www. eecs. berkeley. edu/Research/Projects/CS/vision/grouping/ January, 2017 Math. AM-OIL Workshop 23

Our related Works Image Inpainting Reconstruction of Traffic Density True data S. Kataoka, M. Yasuda and K. Tanaka: JPSJ, 81, 025001, 2012. January, 2017 Math. AM-OIL Workshop reconstruction from 80% missing data S. Kataoka, M. Yasuda, C. Furtlehner and K. Tanaka: Inverse Problems, 30, 025003, 2014. 24

Summary Supervised Learning of Pairwise Markov Random Fields Bayesian Image Modeling by Loopy Belief Propagation and EM algorithm. By introducing Inverse Real Space Renormalization Group Transformations, the computational time can be reduced. January, 2017 Math. AM-OIL Workshop 25

References 1. K. Tanaka, M. Yasuda and D. M. Titterington: Bayesian image 2. 3. 4. 5. modeling by means of generalized sparse prior and loopy belief propagation, Journal of the Physical Society of Japan, vol. 81, vo. 11, article no. 114802, November 2012. K. Tanaka, S. Kataoka, M. Yasuda, Y. Waizumi and C. -T. Hsu: Bayesian image segmentations by Potts prior and loopy belief propagation, Journal of the Physical Society of Japan, vol. 83, no. 12, article no. 124002, December 2014. K. Tanaka, S. Kataoka, M. Yasuda and M. Ohzeki: Inverse renormalization group transformation in Bayesian image segmentations, Journal of the Physical Society of Japan, vol. 84, no. 4, article no. 045001, April 2015. 田中和之著: ベイジアンネットワークの統計的推論の数理, コロナ社, October 2009. 田中和之 (分担執筆): 確率的グラフィカルモデル(鈴木譲, 植野真臣編), 第 8章 マルコフ確率場と確率的画像処理, pp. 195 -228, 共立出版, July 2016 January, 2017 Math. AM-OIL Workshop 26