Statistical Learning in Astrophysics Jens Zimmermann zimmermmppmu mpg

Statistical Learning in Astrophysics Jens Zimmermann zimmerm@mppmu. mpg. de Max-Planck-Institut für Physik, München MPI für extraterrestrische Physik, München Forschungszentrum Jülich Gmb. H Statistical Learning? Three Classes of Learning Methods Applications in Physics Analysis Training the Learning Methods Examples Conclusion Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 1

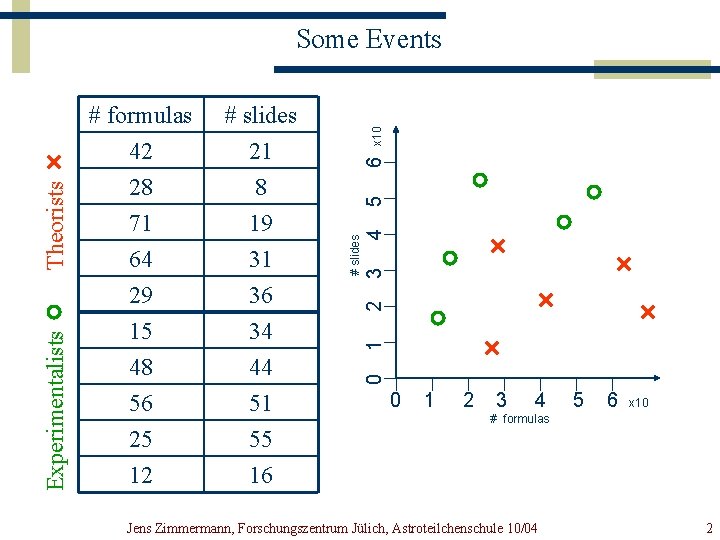
x 10 6 5 4 3 31 36 34 44 51 55 16 2 64 29 15 48 56 25 12 1 # slides 21 8 19 # slides # formulas 42 28 71 0 Experimentalists Theorists Some Events 0 1 2 3 4 5 6 x 10 # formulas Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 2

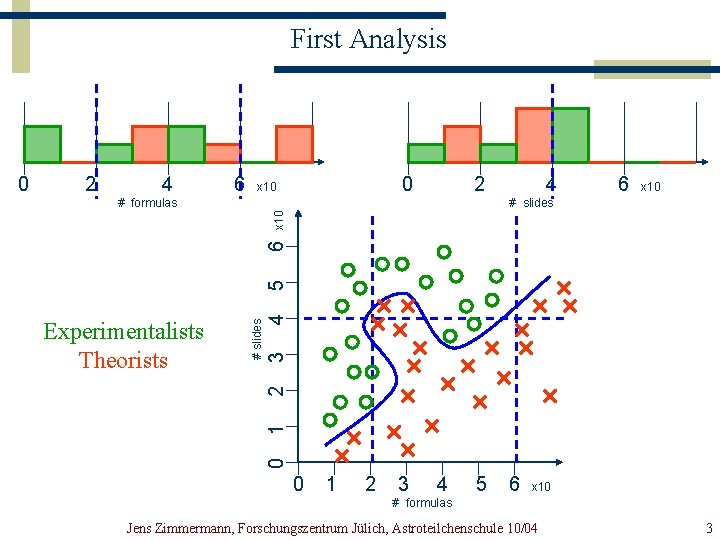
First Analysis 2 4 6 0 x 10 2 4 6 x 10 # slides 3 0 1 2 Experimentalists Theorists 4 5 6 x 10 # formulas # slides 0 0 1 2 3 4 5 6 x 10 # formulas Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 3

Decision Trees # formulas 0 2 #formulas < 20 #formulas > 60 4 6 exp th 20 < #formulas < 60 ? x 10 # slides #slides > 40 #slides < 40 0 2 4 6 #formulas < 20 exp x 10 all events #formulas > 60 rest subset 20 < #formulas < 60 #slides < 40 th exp th th #slides > 40 exp Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 4

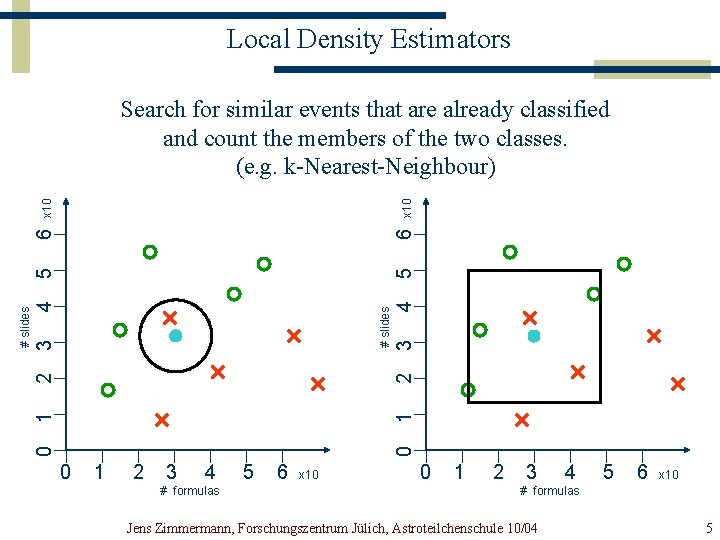
Local Density Estimators x 10 6 5 4 0 1 2 3 # slides 4 3 2 1 0 # slides 5 6 x 10 Search for similar events that are already classified and count the members of the two classes. (e. g. k-Nearest-Neighbour) 0 1 2 3 4 # formulas 5 6 x 10 0 1 2 3 4 5 6 x 10 # formulas Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 5

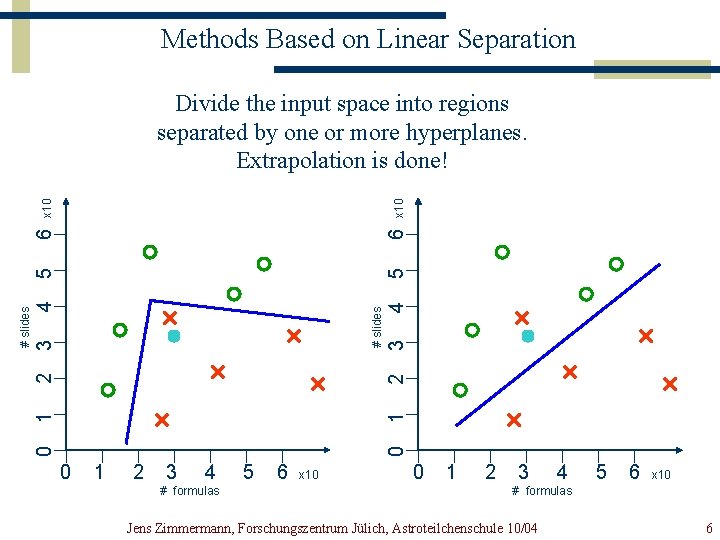
Methods Based on Linear Separation 5 4 2 3 # slides 4 3 2 1 1 0 0 # slides 5 6 6 x 10 Divide the input space into regions separated by one or more hyperplanes. Extrapolation is done! 0 1 2 3 4 # formulas 5 6 x 10 0 1 2 3 4 5 6 x 10 # formulas Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 6

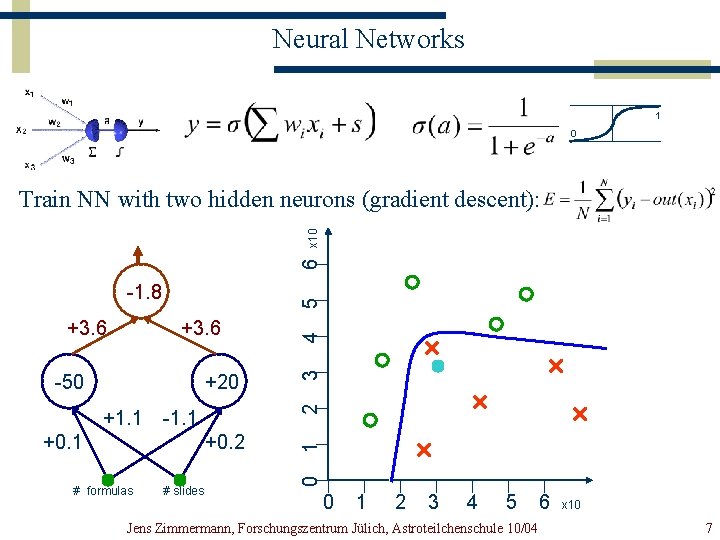
Neural Networks 1 0 6 x 10 Construct Train NN with two hidden separating neuronshyperplanes: (gradient descent): +1. 1 -1. 1 +0. 2 # formulas # slides 4 2 +20 1 -50 3 +3. 6 0 +3. 6 5 -1. 8 0 1 2 3 4 5 Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 6 x 10 7

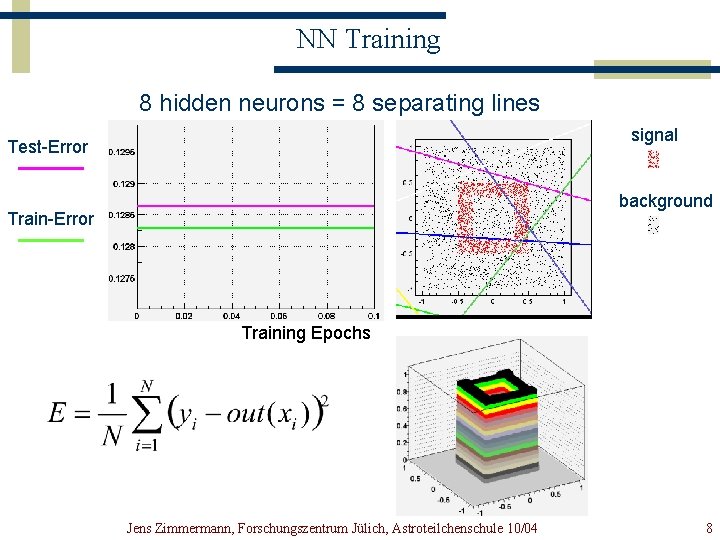
NN Training 8 hidden neurons = 8 separating lines signal Test-Error background Train-Error Training Epochs Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 8

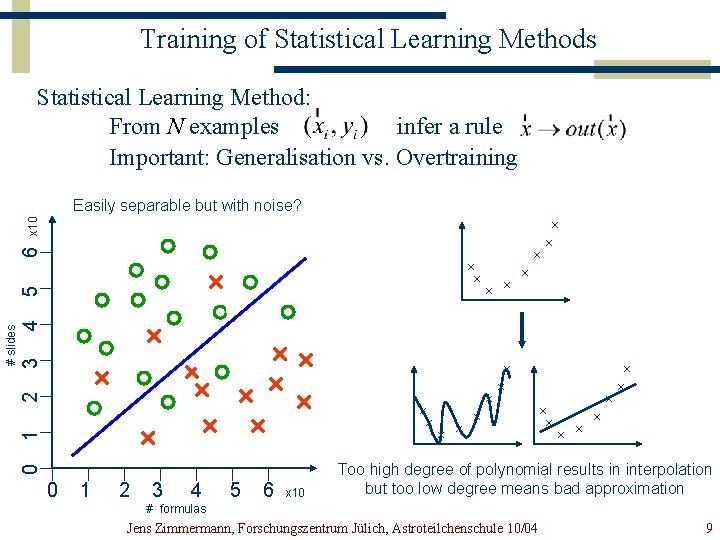
Training of Statistical Learning Methods Statistical Learning Method: From N examples infer a rule Important: Generalisation vs. Overtraining 4 3 2 1 0 # slides 5 6 x 10 Easily Without separable noise and but with separable noise? by complicated boundary? 0 1 2 3 4 5 6 x 10 Too high degree of polynomial results in interpolation but too low degree means bad approximation # formulas Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 9

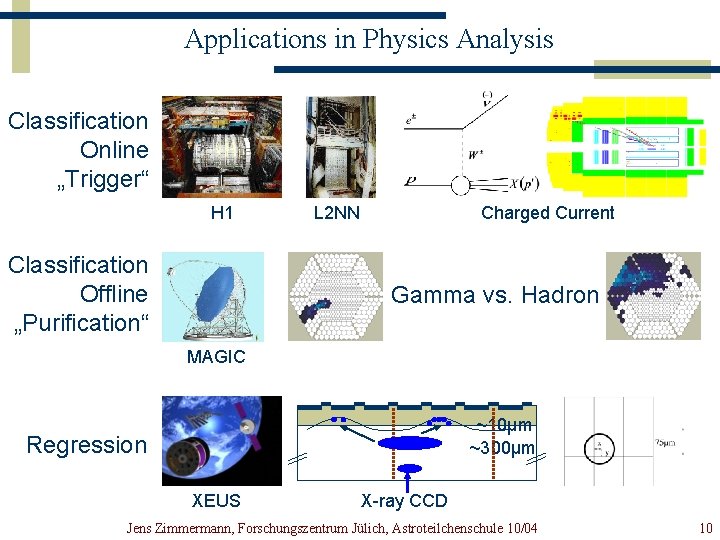
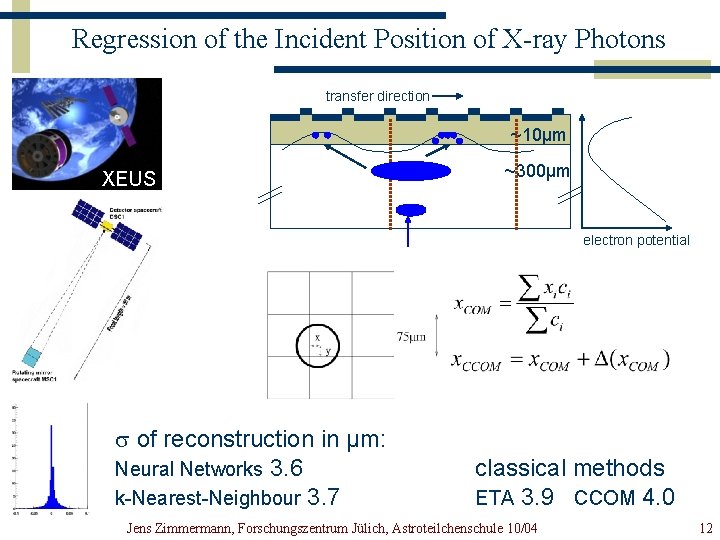
Applications in Physics Analysis Classification Online „Trigger“ H 1 Classification Offline „Purification“ L 2 NN Charged Current Gamma vs. Hadron MAGIC ~10µm ~300µm Regression XEUS X-ray CCD Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 10

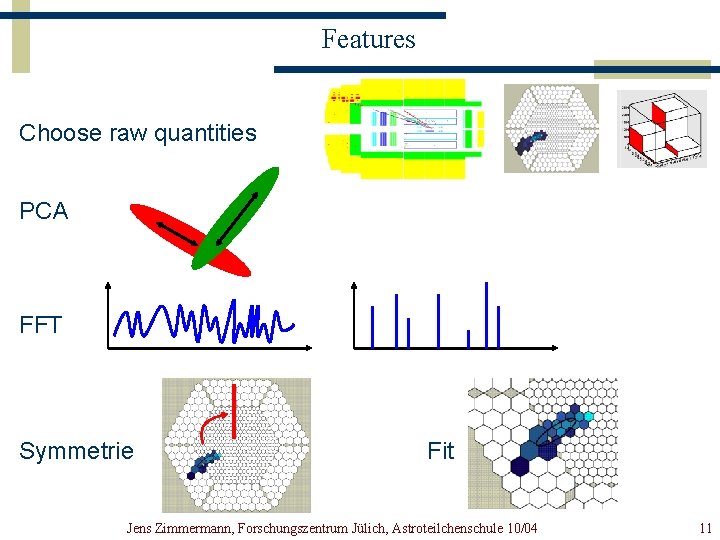
Features Choose raw quantities PCA FFT Symmetrie Fit Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 11

Regression of the Incident Position of X-ray Photons transfer direction ~10µm XEUS ~300µm electron potential s of reconstruction in µm: Neural Networks 3. 6 k-Nearest-Neighbour 3. 7 classical methods ETA 3. 9 CCOM 4. 0 Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 12

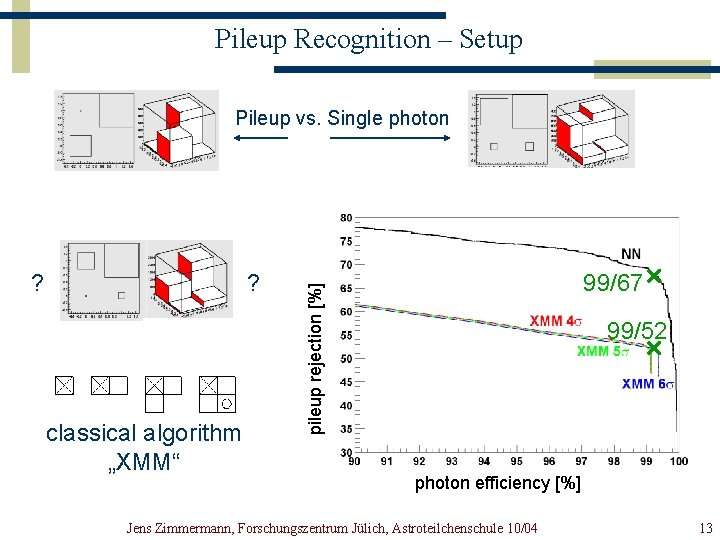
Pileup Recognition – Setup Pileup vs. Single photon ? classical algorithm „XMM“ 99/67 pileup rejection [%] ? 99/52 photon efficiency [%] Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 13

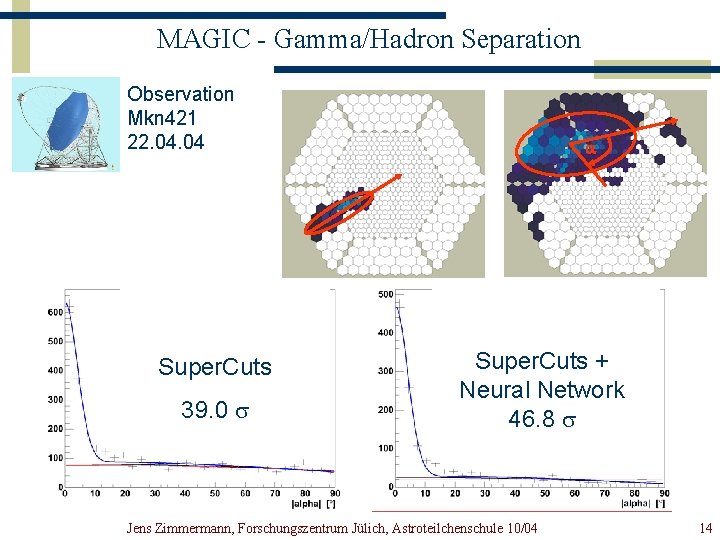
MAGIC - Gamma/Hadron Separation Observation Mkn 421 22. 04 Super. Cuts 39. 0 s a Super. Cuts + Neural Network 46. 8 s Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 14

Conclusion • Three classes of statistical learning methods • Decision Trees (Bagging) 5 C 4. ART m o d Ran t s e r Fo C ur o b h g i e um -N t m s i x e Ma ihood -Near l k • Local Density Estimators e k i L r o t ant s c n i e rk m o V i r t w r c t o s e i p s N D p e l r s u n a i i a r S s • Linear Separation Line ch ly eu a a N n M A • Many applications in current astrophysics experiments and analysis • Compared to classical methods usually at least small improvements Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 15

Theory of Communication: Minimum Description Length Principle Hypothesis H and Data D Bayes 18 th century Our hypothesis should have the maximum probability given the data: Shannon 1948 MDLP Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 Rissanen 1990 16

Statistical Learning Theory: Structural Risk Minimization We have N training events with input xi and correct output yi empirical risk actual risk Relationship is uniform convergence: Upper bound for the actual risk (Vapnik): 1996 h: VC Dimension of learning method (complexity) Create nested subsets of function spaces with rising complexity h 1 < Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 h 2 < h 3 17

Support Vector Machines Separating hyperplane with maximum distance to each datapoint: Maximum margin classifier Found by setting up condition for correct classfication and minimizing which leads to the Lagrangian Necessary condition for a minimum is So the output becomes KKT: only SV have Only linear separation? No! Replace dot products: The mapping to feature space is hidden in a kernel Non-separable case: Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 18

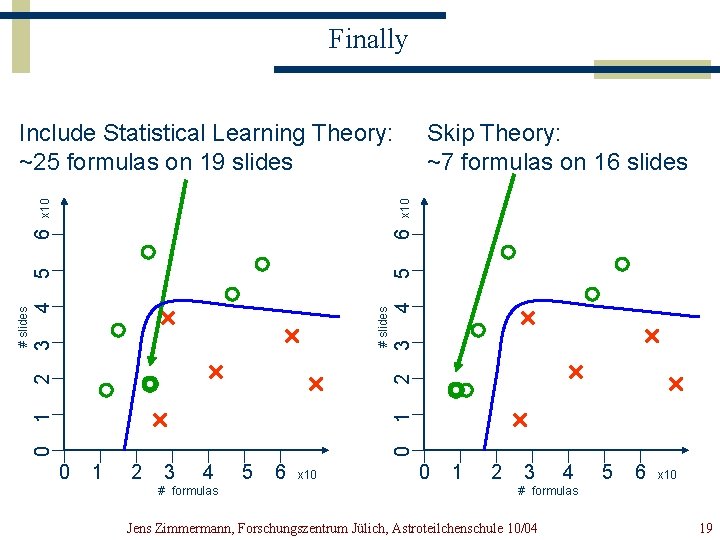
Finally 4 5 6 x 10 Skip Theory: ~7 formulas on 16 slides 0 1 2 3 # slides 4 3 2 1 0 # slides 5 6 x 10 Include Statistical Learning Theory: ~25 formulas on 19 slides 0 1 2 3 4 # formulas 5 6 x 10 0 1 2 3 4 5 6 x 10 # formulas Jens Zimmermann, Forschungszentrum Jülich, Astroteilchenschule 10/04 19