Statistical Learning Dong Liu Dept EEIS USTC Chapter

Statistical Learning Dong Liu Dept. EEIS, USTC

Chapter 4. Supervised Learning: Theory and Practice • Formulation of supervised learning • Statistical learning theory • Beyond ERM • Practice of supervised learning 2021/3/3 Chap 4. Supervised Learning 2

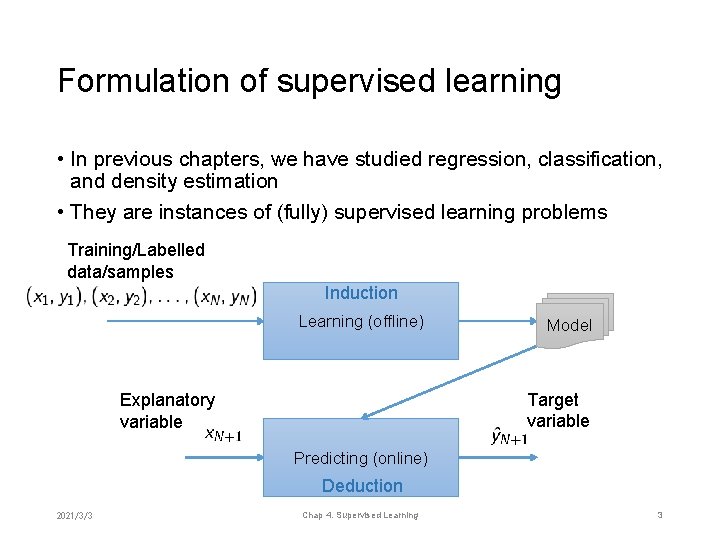
Formulation of supervised learning • In previous chapters, we have studied regression, classification, and density estimation • They are instances of (fully) supervised learning problems Training/Labelled data/samples Induction Learning (offline) Model Target variable Explanatory variable Predicting (online) Deduction 2021/3/3 Chap 4. Supervised Learning 3

Model: deterministic vs. probabilistic • Deterministic model: • Probabilistic model: • If the target variable is discrete, the problem is classification • If the target variable is continuous, the problem is regression • Deterministic model • For classification, is discriminant function • For regression, is regression function • Probabilistic model • Probabilistic density function for classification/regression • Special case: if explanatory variable is empty, the problem is density estimation 2021/3/3 Chap 4. Supervised Learning 4

Model: discriminative vs. generative • Especially in classification • Discriminative model refers to • Generative model refers to • In supervised learning, generative modeling is not necessary • If both generative and discriminative models are learnt, we actually solved the density estimation for • Density estimation is omnipotent in supervised learning 2021/3/3 Chap 4. Supervised Learning 5

Method: discriminative vs. generative • Discriminative methods: directly compute discriminative models • Generative methods: compute not only discriminative but also generative models • Pros and cons • Discriminative methods can easily integrate basis functions, usually perform better on a small training set • Generative methods can easily deal with latent variables, usually converge faster when training data increase 2021/3/3 Chap 4. Supervised Learning 6

Loss functions 1/2 • How to evaluate the prediction result? • For deterministic function, we define • Examples • Quadratic loss • Absolute loss • 0 -1 loss e. g. least squares • For probabilistic function, we usually use log-loss e. g. logistic regression 2021/3/3 Chap 4. Supervised Learning 7

Loss functions 2/2 • Examples of advanced loss functions • Perceptron • SVM 2021/3/3 Chap 4. Supervised Learning 8

Risk functional • Settings • • • Input space Output space Hypothesis space Parameterization Parameter space • Risk functional is a function of loss function (parameter) • Risk minimization is what we want, but not tractable 2021/3/3 Chap 4. Supervised Learning 9

Empirical risk • Based on what we have (training data), we approximate the risk by empirical risk • Empirical risk minimization (ERM) • Least squares is ERM • Maximum likelihood is ERM • … 2021/3/3 Chap 4. Supervised Learning 10

Is ERM a good strategy? • ERM may lead to an ill-posed problem, so we use regularization • ERM cannot incorporate prior information, so we use Bayesian • ERM does not consider the dataset variance, so we use biasvariance tradeoff • ERM does not consider the cost of model storage, so we use minimum description length (MDL) • After all, does ERM guarantee the risk minimization? 2021/3/3 Chap 4. Supervised Learning 11

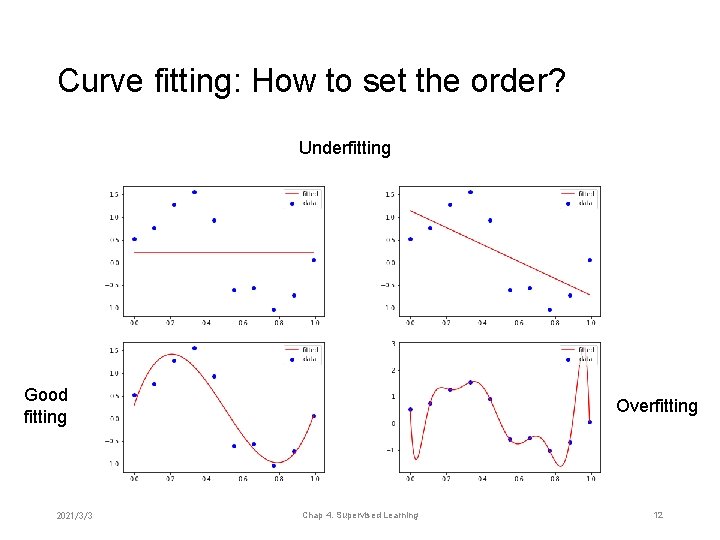
Curve fitting: How to set the order? Underfitting Good fitting 2021/3/3 Overfitting Chap 4. Supervised Learning 12

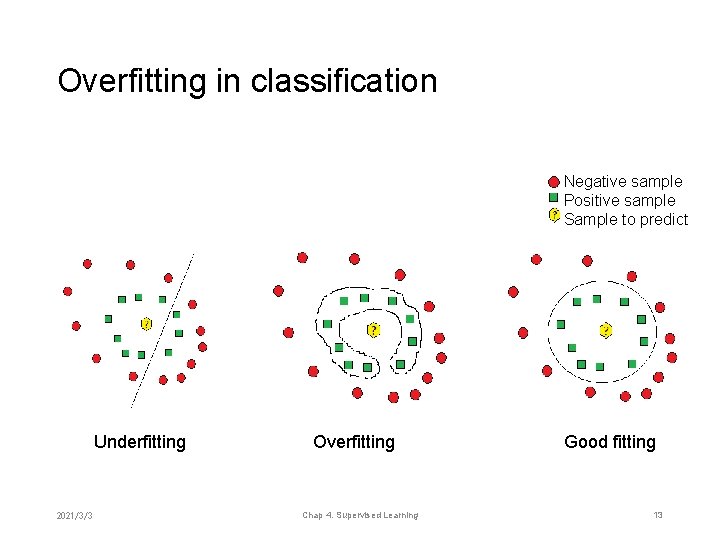
Overfitting in classification Negative sample Positive sample Sample to predict Underfitting 2021/3/3 Overfitting Chap 4. Supervised Learning Good fitting 13

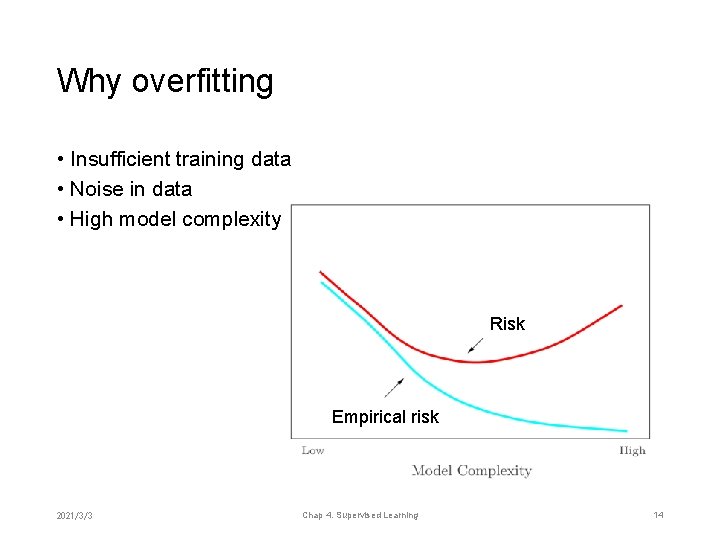
Why overfitting • Insufficient training data • Noise in data • High model complexity Risk Empirical risk 2021/3/3 Chap 4. Supervised Learning 14

Chapter 4. Supervised Learning: Theory and Practice • Formulation of supervised learning • Statistical learning theory • Beyond ERM • Practice of supervised learning 2021/3/3 Chap 4. Supervised Learning 15

Sketch of statistical learning theory • Developed by Vapnik and collaborators during 1960 s~1990 s • For supervised learning (classification, regression, density estimation) • Deal with the relation between empirical risk and risk • Introduce structural risk minimization (SRM) • Lead to SVM V. N. Vapnik (1936 -) 2021/3/3 Chap 4. Supervised Learning 16

Risk vs. Empirical risk • Risk minimization • Depends on loss function, probabilistic measure, parameter space • Empirical risk minimization • Depends on loss function, training data, parameter space • In the following, we consider loss function to be 0 -1 loss for binary classification 2021/3/3 Chap 4. Supervised Learning 17

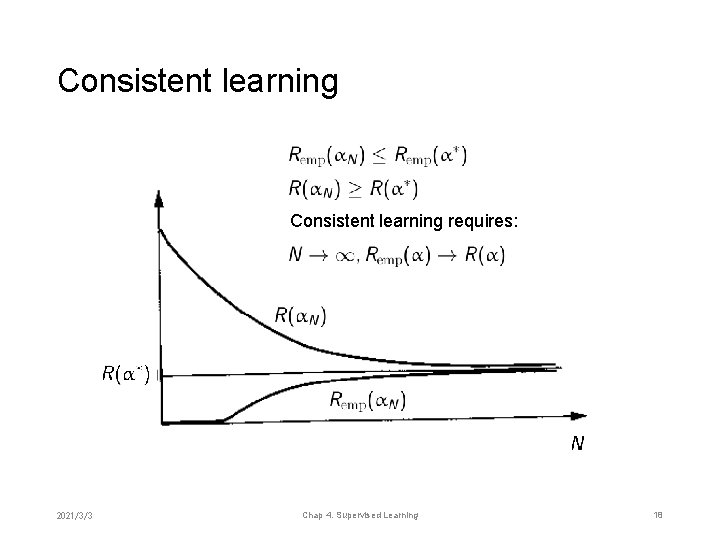
Consistent learning requires: 2021/3/3 Chap 4. Supervised Learning 18

Special case: Finite parameter space • If the parameter space contains only one parameter • According to Hoeffding's inequality (0 -1 loss) Or equivalently, with probability at least • If the parameter space has finite number of parameters, say M, then with probability at least • But many practical learning methods have infinite number! 2021/3/3 Chap 4. Supervised Learning 19

Entropy of a function set 1/2 • Consider binary classification • How many “results” are possible given a dataset and a parameter space? • Define: • Note that we can similarly define this number based on loss function (0 -1 loss), and the number is equal 2021/3/3 Chap 4. Supervised Learning 20

Entropy of a function set 2/2 • Then we define entropy as • Similarly, we define annealed entropy as • And growth function as 2021/3/3 Chap 4. Supervised Learning 21

Important theorems • Theorem 1 (consistent learning) • Theorem 2 (fast convergence) • Theorem 3 2021/3/3 Chap 4. Supervised Learning 22

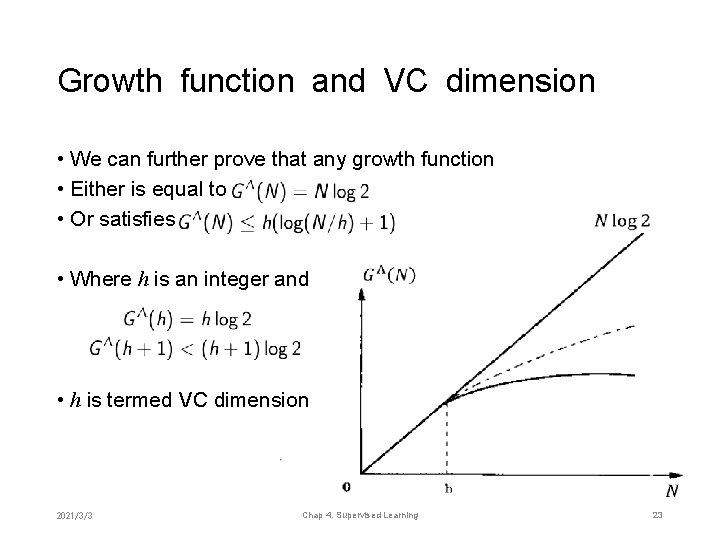
Growth function and VC dimension • We can further prove that any growth function • Either is equal to • Or satisfies • Where h is an integer and • h is termed VC dimension 2021/3/3 Chap 4. Supervised Learning 23

What is VC dimension? • Consider the case that • We say that the function set (with parameter space) can shatter some samples • With adjustable parameter, the function set can produce any possible result on these samples • For example, consider a binary classifier • With adjustable weight • With adjustable bias • With adjustable weight & bias • VC dimension means that: the function set can shatter at most samples 2021/3/3 Chap 4. Supervised Learning 24

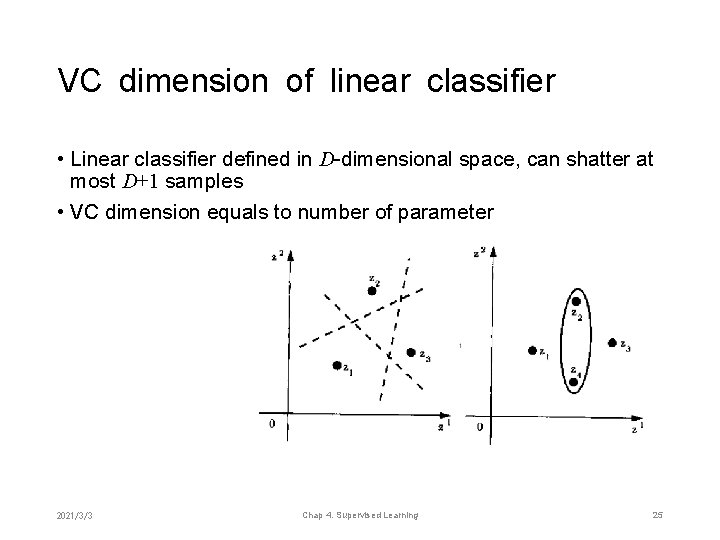
VC dimension of linear classifier • Linear classifier defined in D-dimensional space, can shatter at most D+1 samples • VC dimension equals to number of parameter 2021/3/3 Chap 4. Supervised Learning 25

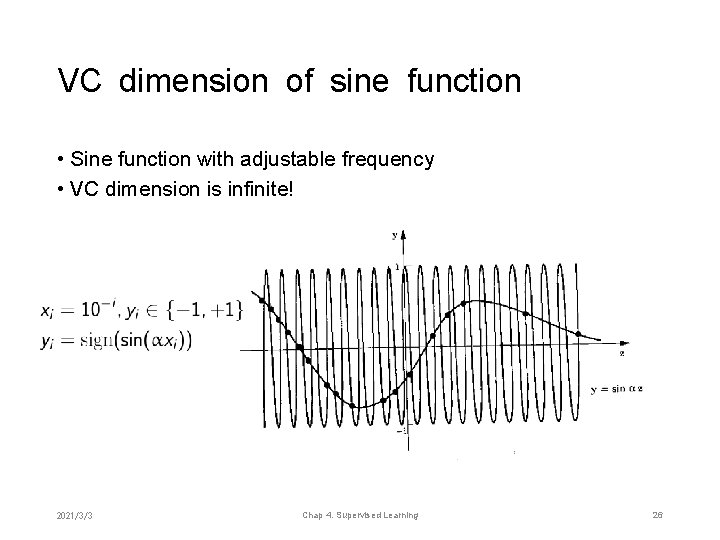
VC dimension of sine function • Sine function with adjustable frequency • VC dimension is infinite! 2021/3/3 Chap 4. Supervised Learning 26

VC dimension of SVM • Consider a restricted linear classifier • And we assume the data points are within a sphere whose radius is , then we have • Thus, the VC dimension of SVM can be much lower than that of ordinary linear classifier 2021/3/3 Chap 4. Supervised Learning 27

Why is VC dimension important? • Intuitively, VC dimension characterizes how powerful a function set is • Infinite VC dimension implies that, for a specific dataset, the function set can always achieve empirical risk equal to 0, i. e. ERM is not informative • We say the function set cannot be falsified (falsifiability, defines science, was proposed by Popper 1968) • Rigorously, VC dimension determines the bound of risk Note: for finite parameter space, we use 2021/3/3 Chap 4. Supervised Learning 28

Notes • VC dimension depicts the “effective volume” of an infinite function set • VC dimensions of many important classifiers (decision tree, neural network) are unknown yet • VC dimension analysis does not apply for non-parametric learning (e. g. k-NN) 2021/3/3 Chap 4. Supervised Learning 29

Chapter 4. Supervised Learning: Theory and Practice • Formulation of supervised learning • Statistical learning theory • Beyond ERM • Practice of supervised learning 2021/3/3 Chap 4. Supervised Learning 30

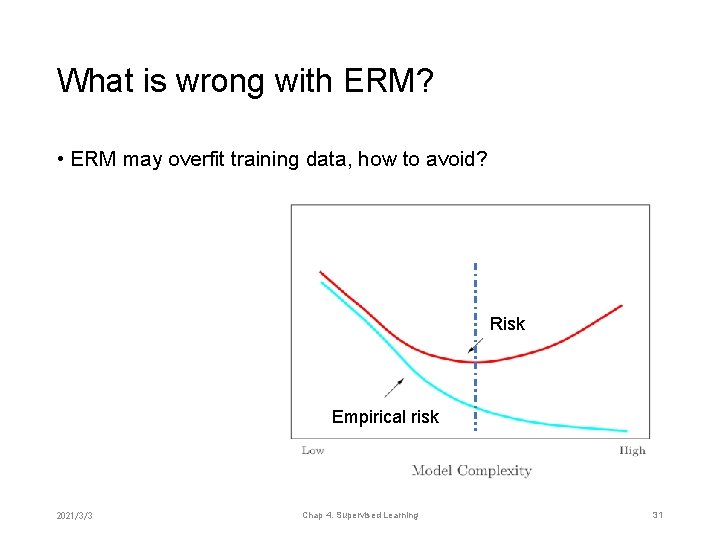
What is wrong with ERM? • ERM may overfit training data, how to avoid? Risk Empirical risk 2021/3/3 Chap 4. Supervised Learning 31

Structural risk minimization (SRM) • According to theory • SRM tries to minimize the sum of ERM and confidence interval 2021/3/3 Chap 4. Supervised Learning 32

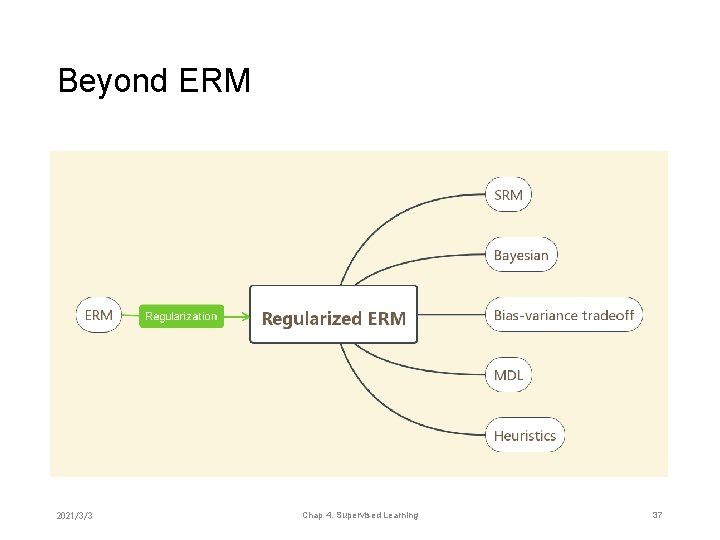
Regularization • SRM is a concrete example of regularization where the regularization term controls model complexity • Regularization was firstly proposed to handle ill-posed problem • Several different ways to interpret/enforce regularization • • 2021/3/3 Bayesian Bias-variance tradeoff Minimum description length (MDL) And heuristics … Chap 4. Supervised Learning 33

Bayesian as regularization • Consider probabilistic modeling • Loss function is log-loss • Minimizing empirical risk is maximizing likelihood • Maximizing posterior requires the prior • Thus, the regularization term is equivalent to • Bayesian vs. SRM • Bayesian needs the prior information • SRM does not require the true model to be within the hypothesis space 2021/3/3 Chap 4. Supervised Learning 34

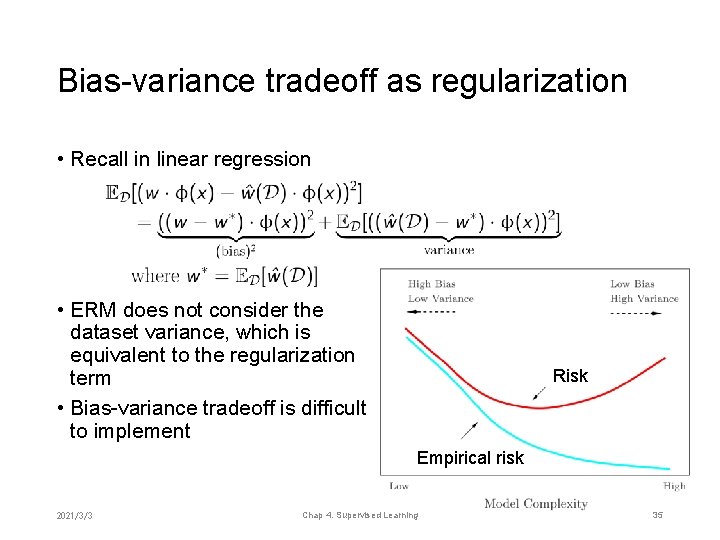
Bias-variance tradeoff as regularization • Recall in linear regression • ERM does not consider the dataset variance, which is equivalent to the regularization term • Bias-variance tradeoff is difficult to implement Risk Empirical risk 2021/3/3 Chap 4. Supervised Learning 35

MDL as regularization • Minimum description length (MDL) principle: the best model achieves the minimum description length for the given dataset • Example: linear classifier • First, we need to encode the model itself • Second, for each data point, we check whether the classification result is correct; if not, we need to encode the correct class • MDL takes into account the cost of model storage, which is equivalent to the regularization term • MDL vs. Bayesian • MDL requires a proper rule of encoding; an ideal coding is related to probability (Shannon 1948) 2021/3/3 Chap 4. Supervised Learning 36

Beyond ERM 2021/3/3 Chap 4. Supervised Learning 37

Philosophy behind Regularized ERM • Occam’s Razor: Numquam ponenda est pluralitas sine necessitate. • We are to admit no more causes of natural things than such as are both true and sufficient to explain their appearances. (Newton) • We prefer simpler theories to more complex ones “because their empirical content is greater; and because they are better testable. ” (Popper) 2021/3/3 Chap 4. Supervised Learning 38

Chapter 4. Supervised Learning: Theory and Practice • Formulation of supervised learning • Statistical learning theory • Beyond ERM • Practice of supervised learning 2021/3/3 Chap 4. Supervised Learning 39

Practice of supervised learning • Typical steps • • • 2021/3/3 Collect a dataset (data cleaning, data augmentation) Decide the form of model (hyper-parameters) Decide the strategy (optimization target) Learn the model (parameters): usually numeric or heuristic optimization Evaluate the model Chap 4. Supervised Learning 40

Dataset • Samples shall represent the problem of interest • Samples shall be independently and identically distributed (i. i. d. ) • Noisy samples and outliers shall be excluded or specially treated • If data are not enough, data augmentation can be applied • Generative modeling helps data augmentation • Heuristics: such as image scaling, rotation, cropping, … 2021/3/3 Chap 4. Supervised Learning 41

Model form/hyper-parameter • We need to consider the following criteria: • Risk: How well does the model perform? • Not only empirical risk! • Computational efficiency • Training efficiency • Predicting efficiency • Scalability • Interpretability: How well can human understand? • Special requirements • Robust to noise/outlier • Can deal with missing attributes 2021/3/3 Chap 4. Supervised Learning 42

Optimization target • Loss function: usually should correspond to evaluation criterion • Evaluation criteria • Accuracy/error rate (for classification), corresponding to 0 -1 loss • MAE/RMSE (for regression), corresponding to absolute/quadratic loss • Cross-entropy/K-L divergence (for density estimation), corresponding to log-loss • Others … 2021/3/3 Chap 4. Supervised Learning 43

Other evaluation criteria 1/2 • Predicted class True class Positive Negative Positive True Positive False Negative False Positive True Negative Example: 100 face samples, 10 belong to “Alice. ” A classifier predicts 12 “Alice” and 7 are correct: Predicted class True class 2021/3/3 Chap 4. Supervised Learning Yes No Yes 7 3 No 5 85 44

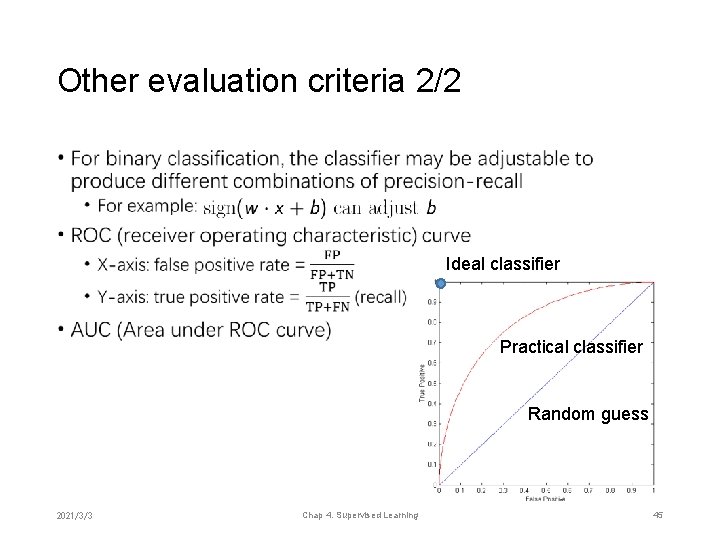
Other evaluation criteria 2/2 • Ideal classifier Practical classifier Random guess 2021/3/3 Chap 4. Supervised Learning 45

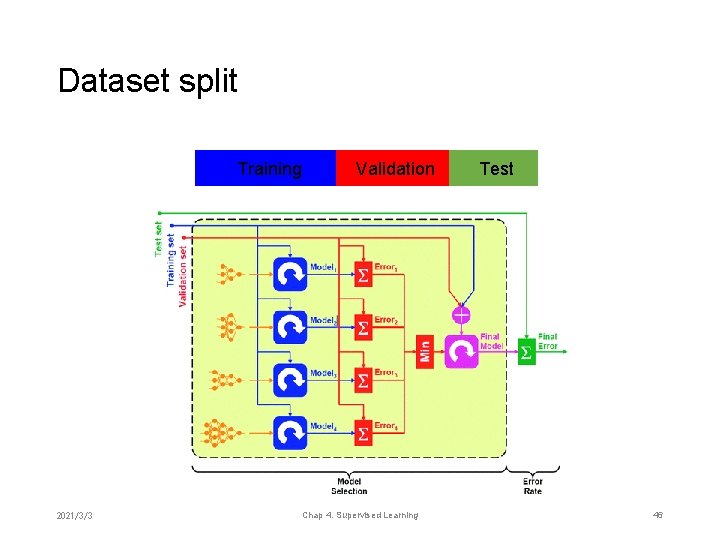
Dataset split Training 2021/3/3 Validation Chap 4. Supervised Learning Test 46

Cross validation • Re-use the data for training and validation • K-fold cross validation • Break up data into groups of the same size • Hold aside one group for validation and use the rest for training • Repeat Usually, K=5 or 10 K=N if data are scarce, “leave one out” • Select the model with the minimum average validation error 2021/3/3 Chap 4. Supervised Learning 47

Chapter summary Dictionary Toolbox • • • Cross validation • Data augmentation • F 1 -value • Minimum description length (MDL) • Precision • Recall • ROC curve, area under ~ (AUC) • Structural risk minimization (SRM) Discriminant/regression function Discriminative/generative method Discriminative/generative model Entropy (of function set) Growth function Loss function Occam’s Razor Overfitting Risk, empirical ~ minimization (ERM), regularized empirical ~ minimization • Supervised learning • Underfitting • VC dimension 2021/3/3 Chap 4. Supervised Learning 48