STATISTICAL INFERENCE PART II SOME PROPERTIES OF ESTIMATORS
































- Slides: 32

STATISTICAL INFERENCE PART II SOME PROPERTIES OF ESTIMATORS 1

SOME PROPERTIES OF ESTIMATORS • θ: a parameter of interest; unknown • Previously, we found good(? ) estimator(s) for θ or its function g(θ). • Goal: • Check how good are these estimator(s). Or are they good at all? • If more than one good estimator is available, which one is better? 2

SOME PROPERTIES OF ESTIMATORS • UNBIASED ESTIMATOR (UE): An estimator is an UE of the unknown parameter , if Otherwise, it is a Biased Estimator of . Bias of for estimating If is UE of , 3

SOME PROPERTIES OF ESTIMATORS • ASYMPTOTICALLY UNBIASED ESTIMATOR (AUE): An estimator is an AUE of the unknown parameter , if 4

SOME PROPERTIES OF ESTIMATORS • CONSISTENT ESTIMATOR (CE): An estimator which converges in probability to an unknown parameter for all is called a CE of . For large n, a CE tends to be closer to the unknown population parameter. • MLEs are generally CEs. 5

EXAMPLE For a r. s. of size n, By WLLN, 6

MEAN SQUARED ERROR (MSE) • The Mean Square Error (MSE) of an estimator for estimating is If is smaller, is a better estimator of . 7

MEAN SQUARED ERROR CONSISTENCY is called mean squared error consistent (or consistent in quadratic mean) if E{ }2 0 as n . Theorem: is consistent in MSE iff i) Var( ) 0 as n . If E{ }2 0 as n , is also a CE of . 8

EXAMPLES X~Exp( ), >0. For a r. s of size n, consider the following estimators of , and discuss their bias and consistency. 9

SUFFICIENT STATISTICS • X, f(x; ), • X 1, X 2, …, Xn • Y=U(X 1, X 2, …, Xn ) is a statistic. • A sufficient statistic, Y, is a statistic which contains all the information for the estimation of . 10

SUFFICIENT STATISTICS • Given the value of Y, the sample contains no further information for the estimation of . • Y is a sufficient statistic (ss) for if the conditional distribution h(x 1, x 2, …, xn|y) does not depend on for every given Y=y. • A ss for is not unique: • If Y is a ss for , then any 1 -1 transformation of Y, say Y 1=fn(Y) is also a ss for . 11

SUFFICIENT STATISTICS • The conditional distribution of sample rvs given the value of y of Y, is defined as • If Y is a ss for , then ss for Not depend on for every given y. may include y or constant. 12 • Also, the conditional range of Xi given y not depend on .

SUFFICIENT STATISTICS EXAMPLE: X~Ber(p). For a r. s. of size n, show that is a ss for p. 13

SUFFICIENT STATISTICS • Neyman’s Factorization Theorem: Y is a ss for iff The likelihood function Does not depend on xi except through y Not depend on (also in the range of xi. ) where k 1 and k 2 are non-negative functions. 14

EXAMPLES 1. X~Ber(p). For a r. s. of size n, find a ss for p if exists. 15

EXAMPLES 2. X~Beta(θ, 2). For a r. s. of size n, find a ss for θ. 16

SUFFICIENT STATISTICS • A ss, that reduces the dimension, may not exist. • Jointly ss (Y 1, Y 2, …, Yk ) may be needed. Example: Example 10. 2. 5 in Bain and Engelhardt (page 342 in 2 nd edition), X(1) and X(n) are jointly ss for • If the MLE of exists and unique and if a ss for exists, then MLE is a function of a ss for . 17

EXAMPLE X~N( , 2). For a r. s. of size n, find jss for and 2. 18

MINIMAL SUFFICIENT STATISTICS • If is a ss for θ, then, is also a ss for θ. But, the first one does a better job in data reduction. A minimal ss achieves the greatest possible reduction. 19

MINIMAL SUFFICIENT STATISTICS • A ss T(X) is called minimal ss if, for any other ss T’(X), T(x) is a function of T’(x). • THEOREM: Let f(x; ) be the pmf or pdf of a sample X 1, X 2, …, Xn. Suppose there exist a function T(x) such that, for two sample points x 1, x 2, …, xn and y 1, y 2, …, yn, the ratio is constant with respect to iff T(x)=T(y). Then, T(X) is a minimal sufficient statistic for . 20

EXAMPLE • X~N( , 2) where 2 is known. For a r. s. of size n, find minimal ss for . Note: A minimal ss is also not unique. Any 1 -to-1 function is also a minimal ss. 21

ANCILLARY STATISTIC • A statistic S(X) whose distribution does not depend on the parameter is called an ancillary statistic. • Unlike a ss, an ancillary statistic contains no information about . 22

Example • Example 6. 1. 8 in Casella & Berger, page 257: Let Xi~Unif(θ, θ+1) for i=1, 2, …, n Then, range R=X(n)-X(1) is an ancillary statistic because its pdf does not depend on θ. 23

COMPLETENESS • Let {f(x; ), } be a family of pdfs (or pmfs) and U(x) be an arbitrary function of x not depending on . If requires that the function itself equal to 0 for all possible values of x; then we say that this family is a complete family of pdfs (or pmfs). i. e. , the only unbiased estimator of 0 is 0 itself. 24

EXAMPLES 1. Show that the family {Bin(n=2, ); 0< <1} is complete. 25

EXAMPLES 2. X~Uniform( , ). Show that the family {f(x; ), >0} is not complete. 26

COMPLETE AND SUFFICIENT STATISTICS (css) • Y is a complete and sufficient statistic (css) for if Y is a ss for and the family is complete. The pdf of Y. 1) Y is a ss for . 2) u(Y) is an arbitrary function of Y. E(u(Y))=0 for all implies that u(y)=0 27 for all possible Y=y.

BASU THEOREM • If T(X) is a complete and minimal sufficient statistic, then T(X) is independent of every ancillary statistic. • Example: X~N( , 2). (n-1)S 2/ 2~ S 2 Ancillary statistic for By Basu theorem, and S 2 are independent. 28

BASU THEOREM • Example: X 1, X 2~N( , 2), independent, 2 known. • Let T=X 1+ X 2 and U=X 1 - X 2 • We know that T is a complete minimal ss. • U~N(0, 2 2) distribution free of T and U are independent by Basu’s Theorem 29

Problems • Let be a random sample from a Bernoulli distribution with parameter p. a) Find the maximum likelihood estimator (MLE) of p. b) Is this an unbiased estimator of p? 30

Problems • If Xi are normally distributed random variables with mean μ and variance σ2, what is an unbiased estimator of σ2? 31

Problems • Suppose that are i. i. d. random variables on the interval [0; 1] with the density function, where α> 0 is a parameter to be estimated from the sample. Find a sufficient statistic for α. 32
 Least square property
Least square property Chebyshev inequality proof
Chebyshev inequality proof Probability and statistical inference 9th solution pdf
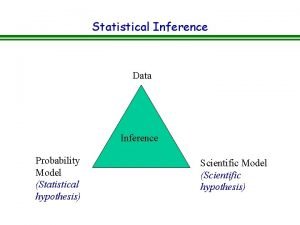
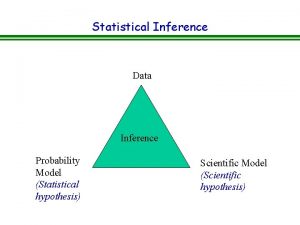
Probability and statistical inference 9th solution pdf Statistical inference
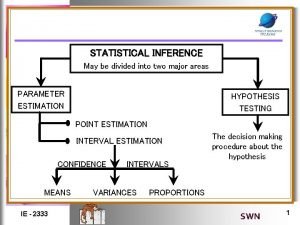
Statistical inference What is a point estimate in statistics
What is a point estimate in statistics Statistical inference is concerned with
Statistical inference is concerned with Statistical inference is divided into
Statistical inference is divided into They say it only takes a little faith to move a mountain
They say it only takes a little faith to move a mountain God when you choose to leave mountains unmovable
God when you choose to leave mountains unmovable Countable and uncountable cake
Countable and uncountable cake Contact and noncontact forces
Contact and noncontact forces Some say the world will end in fire some say in ice
Some say the world will end in fire some say in ice Some say the world will end in fire some say in ice
Some say the world will end in fire some say in ice Some trust in chariots and some in horses song
Some trust in chariots and some in horses song Chemical properties of matter
Chemical properties of matter Some properties of glass
Some properties of glass Intensive vs extensive properties
Intensive vs extensive properties Chemical property of water
Chemical property of water 7-3 multiplication properties of exponents
7-3 multiplication properties of exponents 3-2 properties of parallel lines
3-2 properties of parallel lines Addition symbol
Addition symbol Part to part ratio definition
Part to part ratio definition Part part whole
Part part whole Technical object description example
Technical object description example Bar die is a part of
Bar die is a part of The phase of the moon you see depends on ______.
The phase of the moon you see depends on ______. Two way anova minitab 17
Two way anova minitab 17 Gss recruitment
Gss recruitment Using statistical measures to compare populations
Using statistical measures to compare populations Partition function in statistical mechanics
Partition function in statistical mechanics Statistical mechanics
Statistical mechanics Classical equipartition
Classical equipartition Statistical displays
Statistical displays