Statistical image reconstruction MLEM back projection model OSEM

Statistical image reconstruction • MLEM • (back) projection model • OSEM • MAP –uniform resolution –anatomical prior –lesion detection

MLEM maximum likelihood expectation maximisation

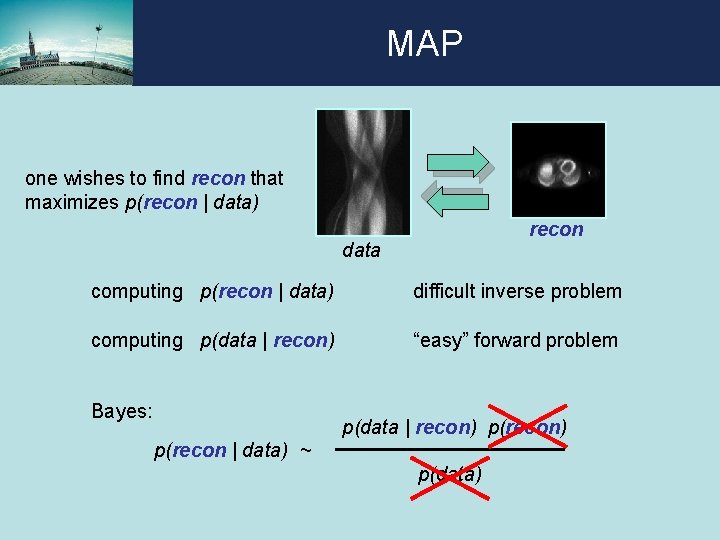
Maximum Likelihood one wishes to find recon that maximizes p(recon | data) recon data computing p(recon | data) difficult inverse problem computing p(data | recon) “easy” forward problem Bayes: p(data | recon) p(recon | data) = ~ p(data)

Maximum Likelihood p(recon | data) ~ p(data | recon) recon projection data Poisson lj p(data | recon) j = 1. . J i = 1. . I ln(p(data | recon)) =~ L(data | recon) =

Maximum Likelihood L(data | recon) find recon: Iterative inversion needed

Expectation Maximisation ML-EM algorithm: • produces non-negative solution • can be written as additive gradient ascent: • several useful alternative derivations exist

Expectation Maximisation Optimisation transfer L(data | recon) L likelihood F In every iteration: = F(data | recon) lcurrent with L(data | lcurrent) = F(data | lcurrent) new llcurrent l

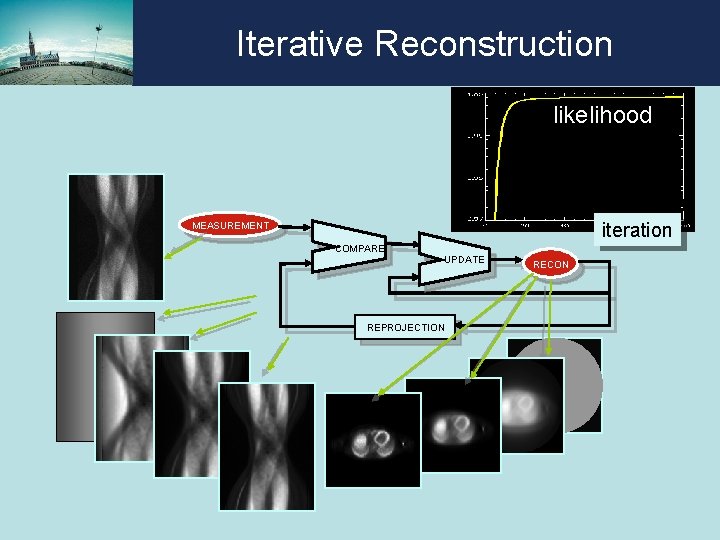
Iterative Reconstruction likelihood iteration MEASUREMENT COMPARE UPDATE REPROJECTION RECON

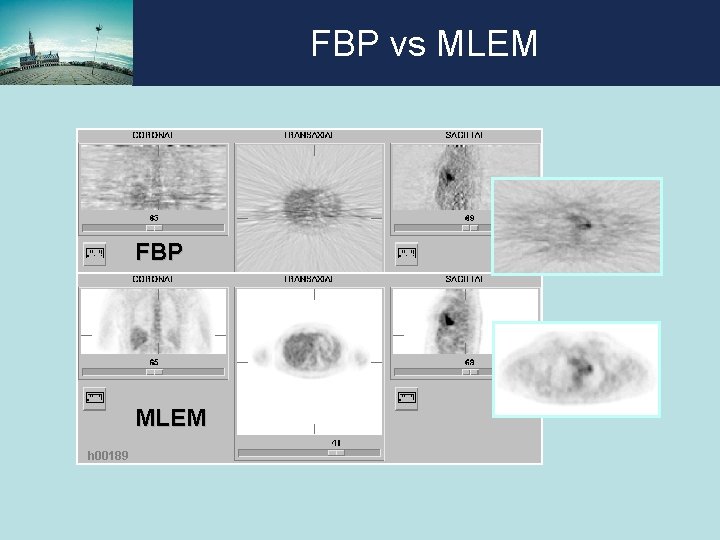
FBP vs MLEM FBP MLEM h 00189

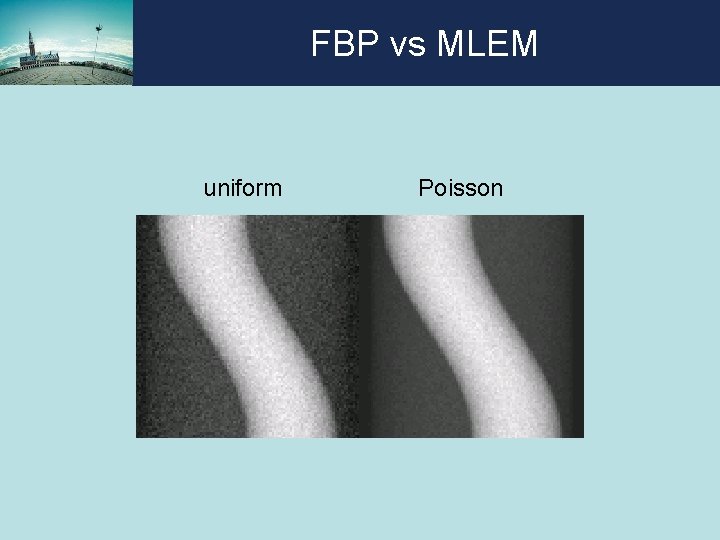
FBP vs MLEM uniform Poisson

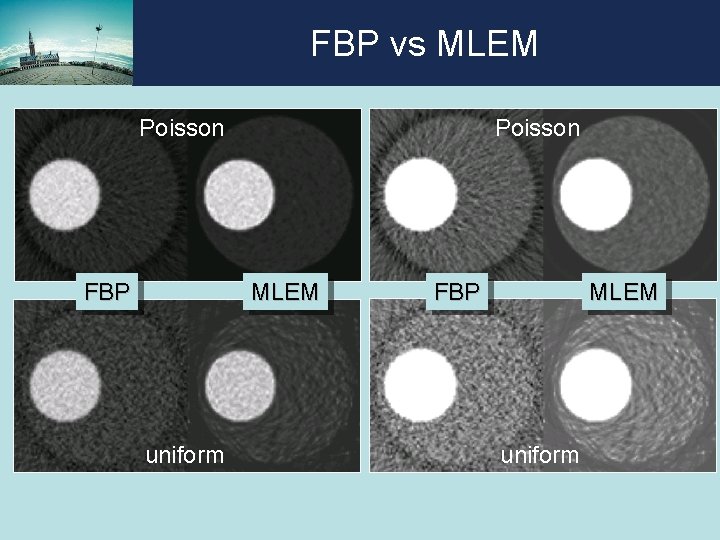
FBP vs MLEM Poisson FBP Poisson MLEM uniform FBP MLEM uniform

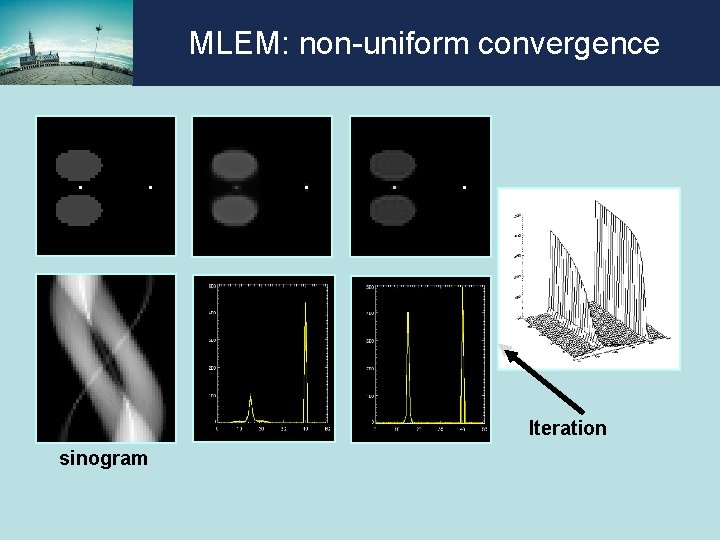
MLEM: non-uniform convergence True image 20 iterations 100 iterations Iteration sinogram

MLEM: non-uniform convergence true image sinogram 8 iter 100 iter FBP with noise smoothed

(back) projection model: model for image resolution

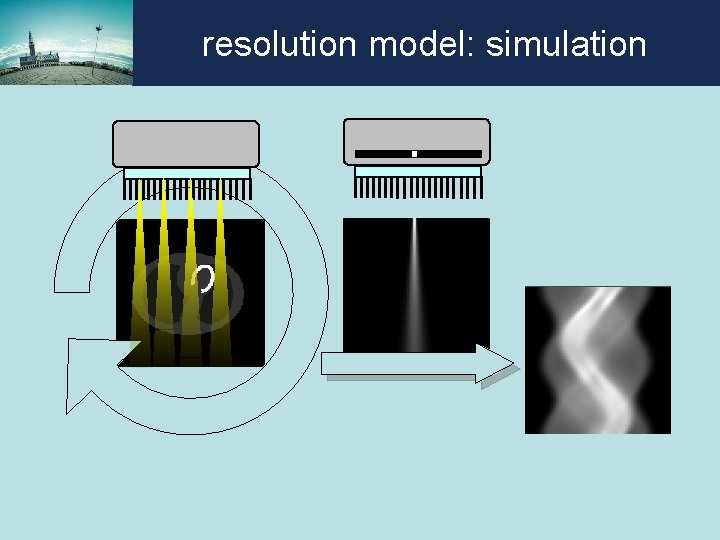
resolution model: simulation

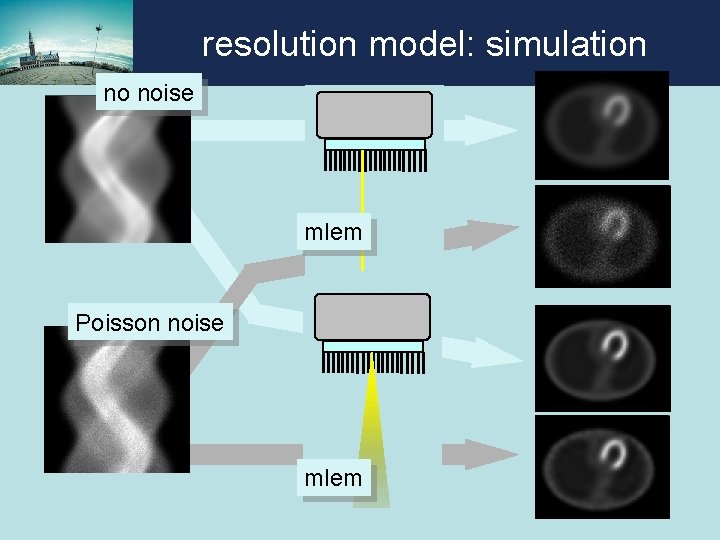
resolution model: simulation no noise mlem Poisson noise mlem

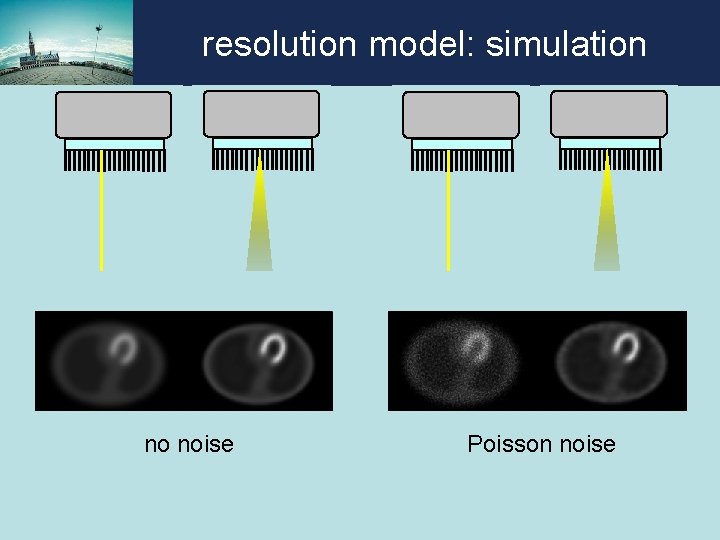
resolution model: simulation no noise Poisson noise

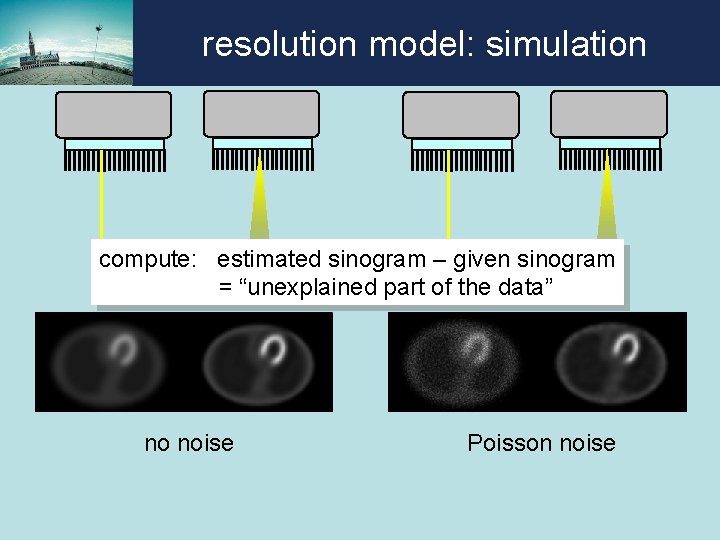
resolution model: simulation compute: estimated sinogram – given sinogram = “unexplained part of the data” no noise Poisson noise

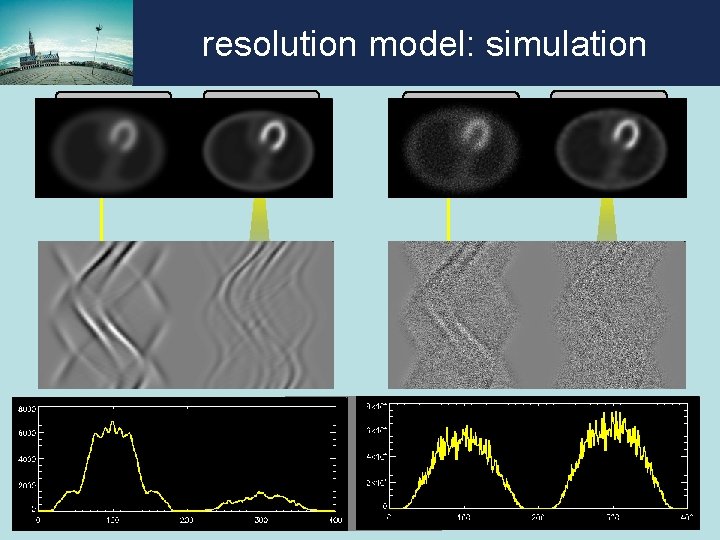
resolution model: simulation compute sum of squared differences along vertical lines

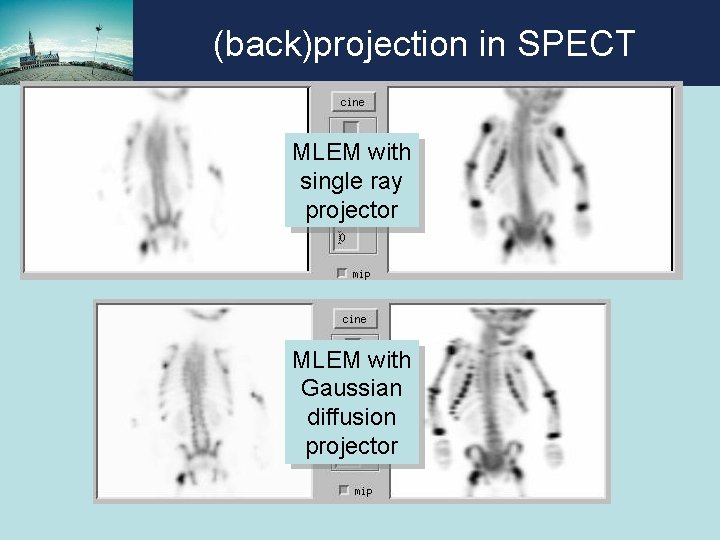
(back)projection in SPECT MLEM with single ray projector MLEM with Gaussian diffusion projector

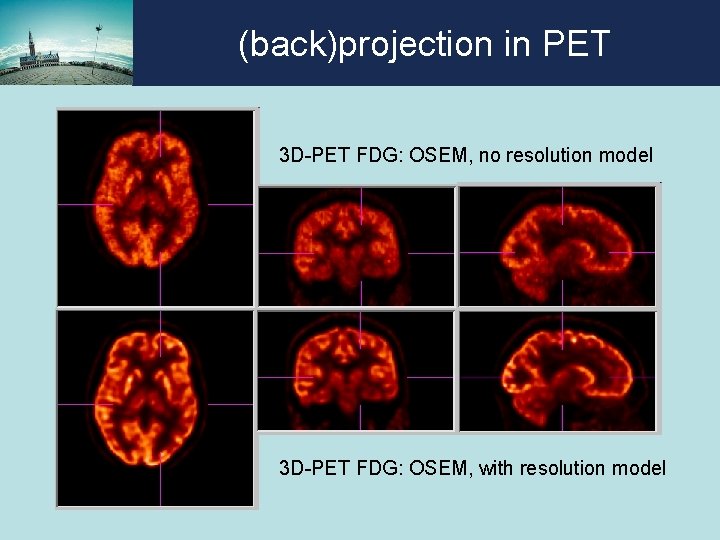
(back)projection in PET 3 D-PET FDG: OSEM, no resolution model 3 D-PET FDG: OSEM, with resolution model

(back) projection model accurate modeling of the physics: • larger fraction of the data becomes consistent better resolution • larger fraction of the noise becomes inconsistent less noise we gain twice! but computation time goes up. . .

OSEM ordered subsets expectation maximisation

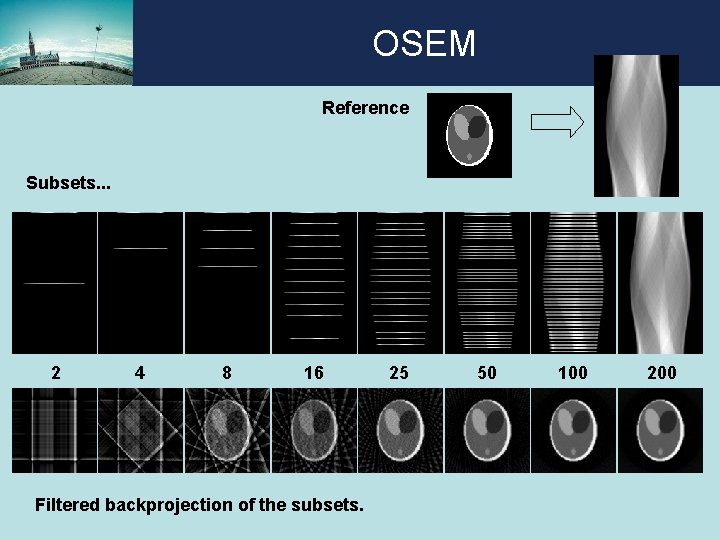
OSEM Reference Subsets. . . 2 4 8 16 Filtered backprojection of the subsets. 25 50 100 200

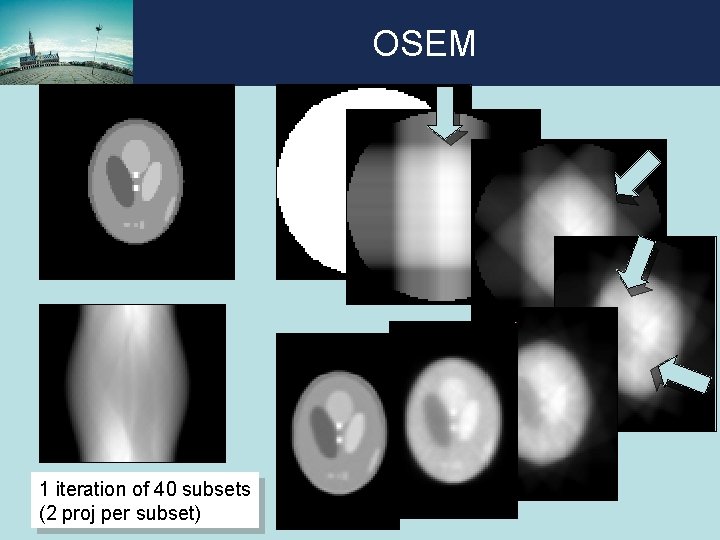
OSEM 0 1 2 3 40 1 iteration of 40 subsets (2 proj per subset) 10 4

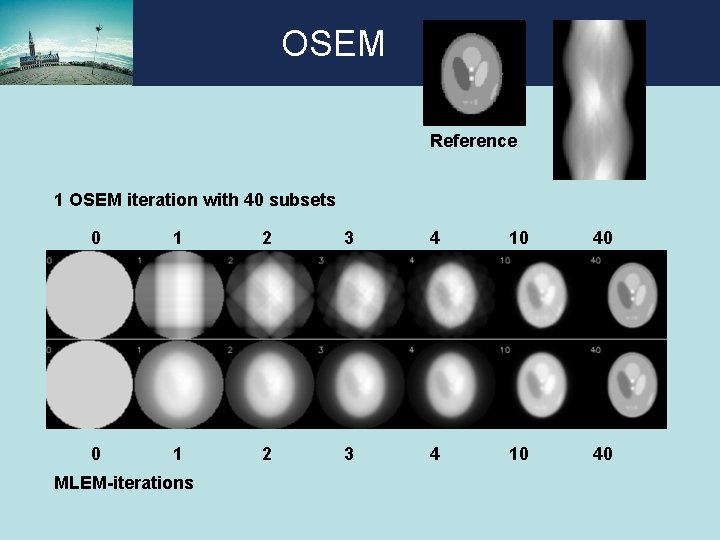
OSEM Reference 1 OSEM iteration with 40 subsets 0 1 2 3 4 10 40 MLEM-iterations

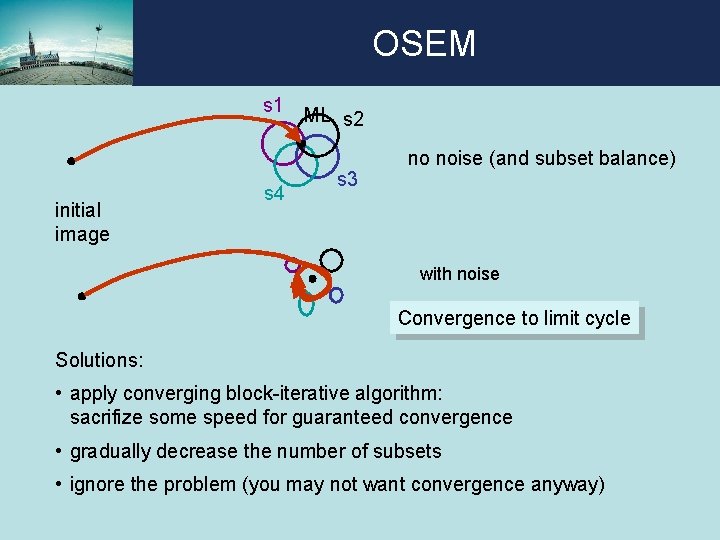
OSEM s 1 initial image s 4 ML s 2 s 3 no noise (and subset balance) with noise Convergence to limit cycle Solutions: • apply converging block-iterative algorithm: sacrifize some speed for guaranteed convergence • gradually decrease the number of subsets • ignore the problem (you may not want convergence anyway)

OSEM true 64 x 1 1 x 64 difference

MAP maximum a posteriori • short intro • MAP • uniform resolution • anatomical priors • lesion detection

MAP one wishes to find recon that maximizes p(recon | data) recon data computing p(recon | data) difficult inverse problem computing p(data | recon) “easy” forward problem Bayes: p(data | recon) p(recon | data) = ~ p(data)

MAP Bayes: p(recon | data) ~ p(data | recon) p(recon) ln p(recon | data) ~ ln p(data | recon) + ln p(recon) posterior likelihood prior - penalty local prior or Markov prior: p(reconj | recon) = p(reconj | reconk, k is neighbor of j) Gibbs distribution: p(reconj | recon) = ln p(reconj | recon) = -bj Ej(Nj) + constant j k

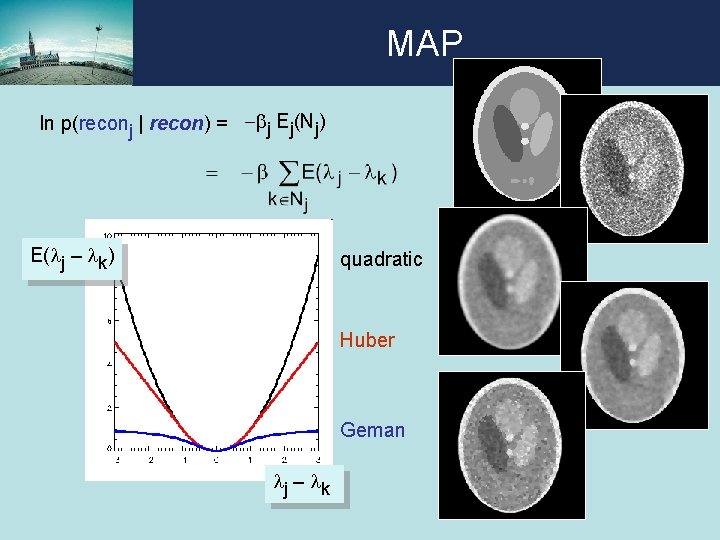
MAP ln p(reconj | recon) = -bj Ej(Nj) E(lj – lk) quadratic Huber Geman lj – lk

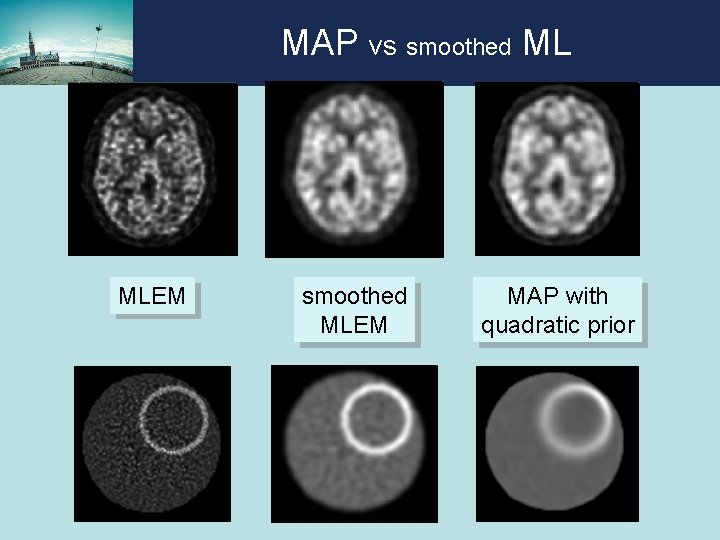
MAP vs smoothed ML MLEM smoothed MLEM MAP with quadratic prior

MAP with uniform resolution Likelihood provides non-uniform information: • some information is destroyed by • attenuation • Poisson noise • finite detector sensitivity and resolution • . . . Use non-uniform “prior” to smooth • more where likelihood is “strong” • less where likelihood is “weak” When postsmoothed-MLEM and MAP have same resolution, resolution they have same covariance! covariance

MAP with uniform resolution • equivalent to post-smoothed MLEM • prior improves condition number: – MAP converges faster than MLEM: • fewer iterations required! • but more work per iteration

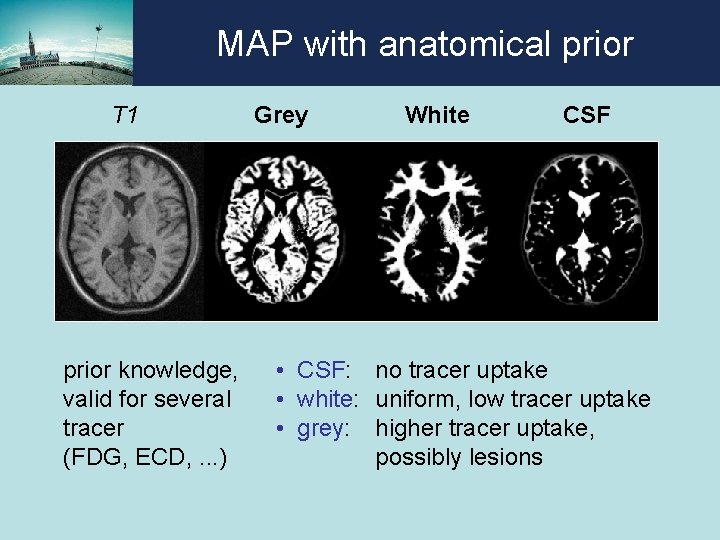
MAP with anatomical prior T 1 prior knowledge, valid for several tracer (FDG, ECD, . . . ) Grey White CSF • CSF: no tracer uptake • white: uniform, low tracer uptake • grey: higher tracer uptake, possibly lesions

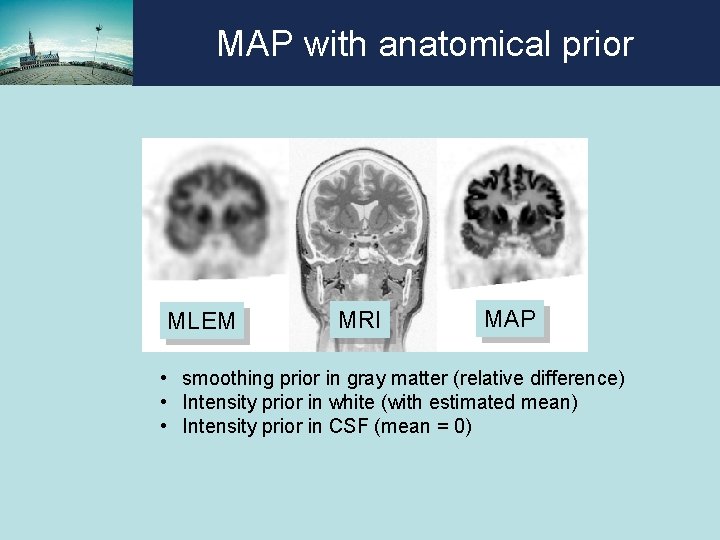
MAP with anatomical prior MLEM MRI MAP • smoothing prior in gray matter (relative difference) • Intensity prior in white (with estimated mean) • Intensity prior in CSF (mean = 0)

MAP with anatomical prior Theoretical analysis indicates that PV-correction with MAP-reconstruction is superior to PV-correction with post-processed MLEM

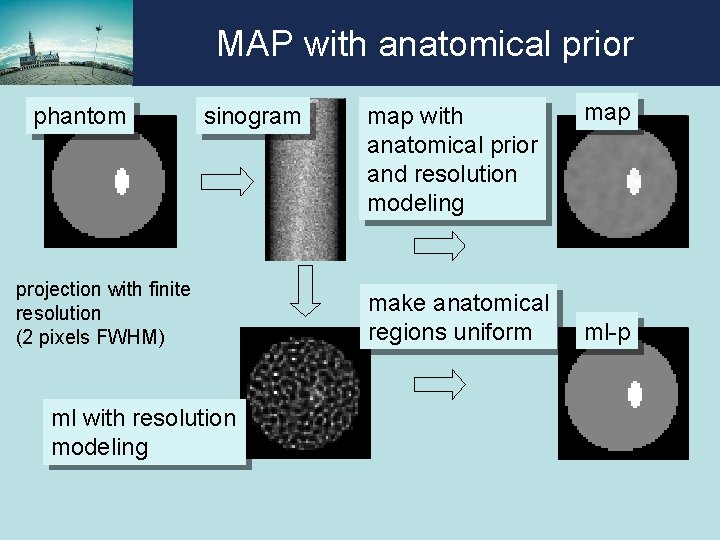
MAP with anatomical prior phantom sinogram projection with finite resolution (2 pixels FWHM) ml with resolution modeling map with anatomical prior and resolution modeling make anatomical regions uniform map ml-p

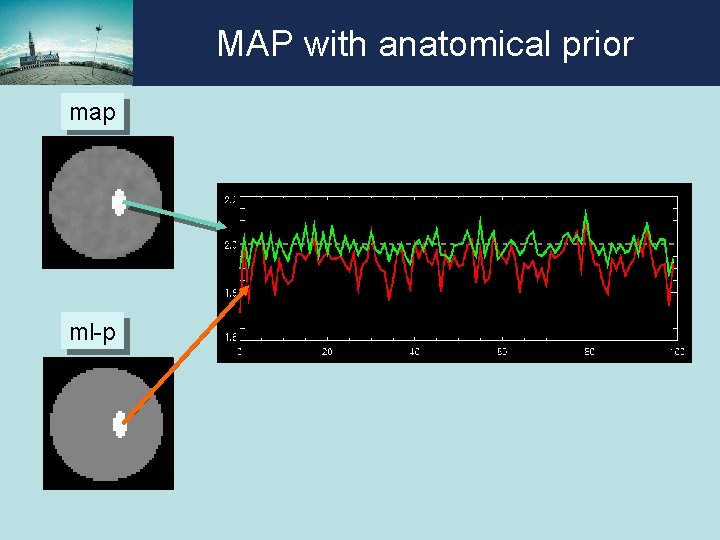
MAP with anatomical prior map ml-p

MAP with anatomical prior MAP yields better noise characteristics than post-processed MLEM

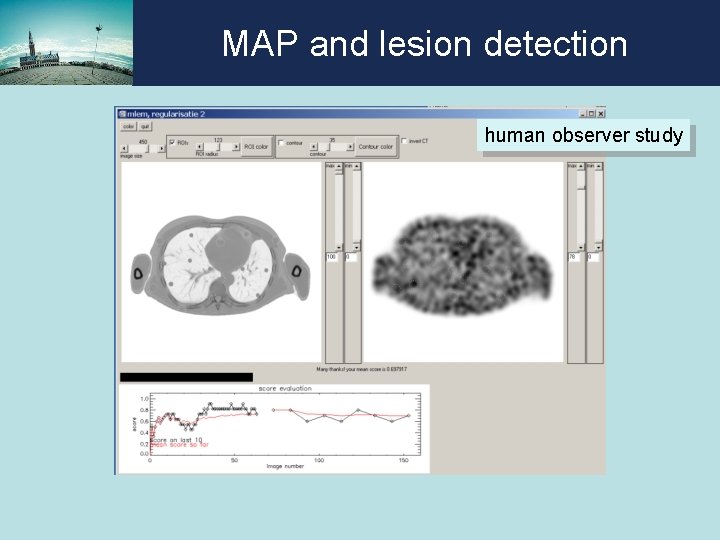
MAP and lesion detection human observer study

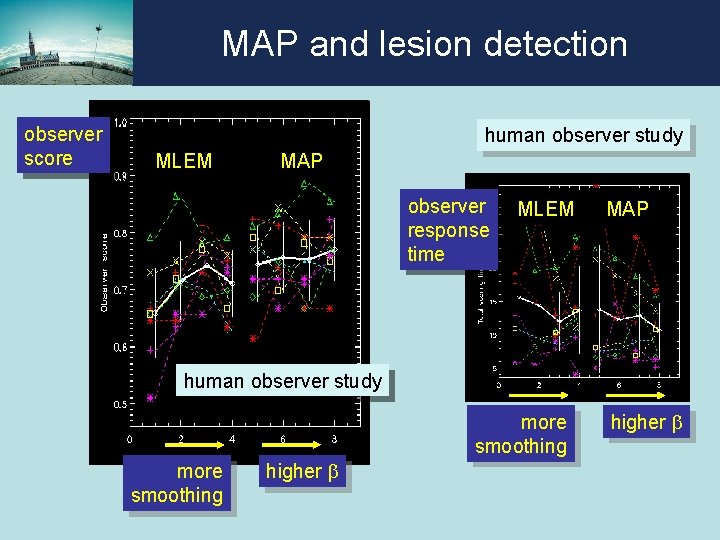
MAP and lesion detection observer score human observer study MLEM MAP observer response time MLEM MAP human observer study more smoothing higher b

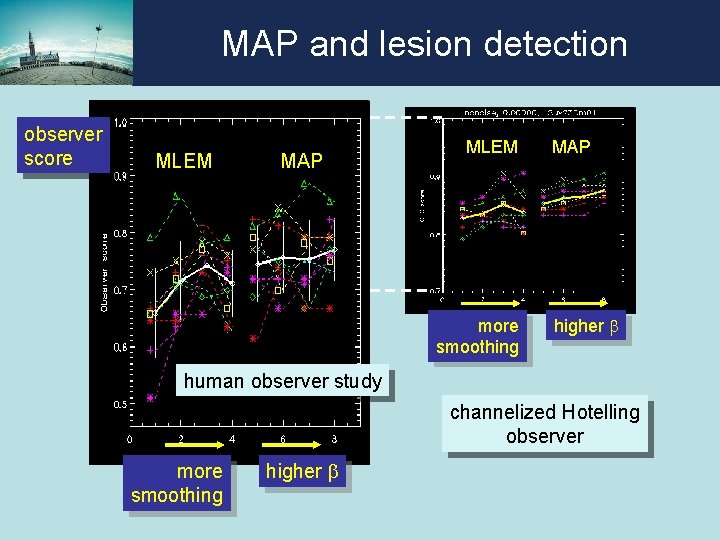
MAP and lesion detection observer score MLEM MAP MLEM more smoothing MAP higher b human observer study channelized Hotelling observer more smoothing higher b

MAP and lesion detection (non-uniform quadratic) MAP seems better for lesion detection

thanks