Statistical Estimation Point Estimate Use a Single Value

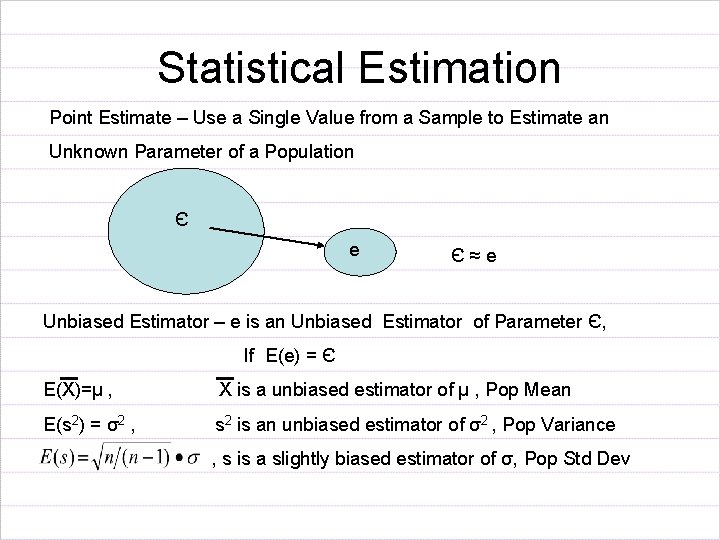
Statistical Estimation Point Estimate – Use a Single Value from a Sample to Estimate an Unknown Parameter of a Population Є e Є≈e Unbiased Estimator – e is an Unbiased Estimator of Parameter Є, If E(e) = Є E(X)=µ , X is a unbiased estimator of µ , Pop Mean E(s 2) = σ2 , s 2 is an unbiased estimator of σ2 , Pop Variance , s is a slightly biased estimator of σ, Pop Std Dev

Interval Estimate – Bound the Parameter between a Upper and Lower Limit ≤ Parameter ≤ Upper Limit X - e ≤ µ ≤ X + e e – Error Bound – Maximum difference between X and µ which we expect to occur. α – Risk – Probability that the difference between X and µ will exceed e. We know from the Central Limit Theorem that the distribution for X will be Normal if we have a large enough sample size.

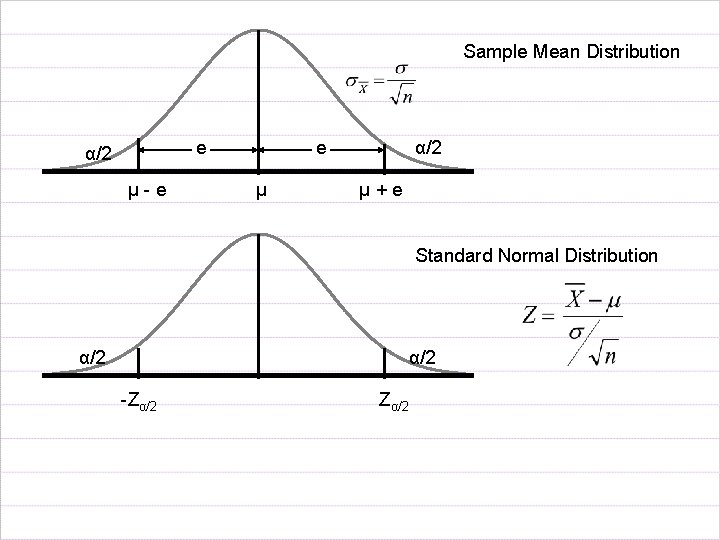
Sample Mean Distribution e α/2 µ-e e µ α/2 µ+e Standard Normal Distribution α/2 -Zα/2

Interval Estimate - X – e ≤ µ ≤ X + e where and n ≥ 30 so σ ≈ s Ex: n = 36, X = 20. 6 yr and s = 3 yr with α =. 05 Confidence Level – C = ( 1 – α )

Ex: n = 64, X = 42, 000 miles, s = 10, 000 miles with C =. 90 & α =. 10 Sample Size Calculation – Use sample size to control the error

Ex: Sample Size to Determine Ave Age for e =. 5 yr, σ = 3 yr, C =. 95

Ex: Sample Size for Ave Cost at WSU for e = $250, σ = ? , C =. 95

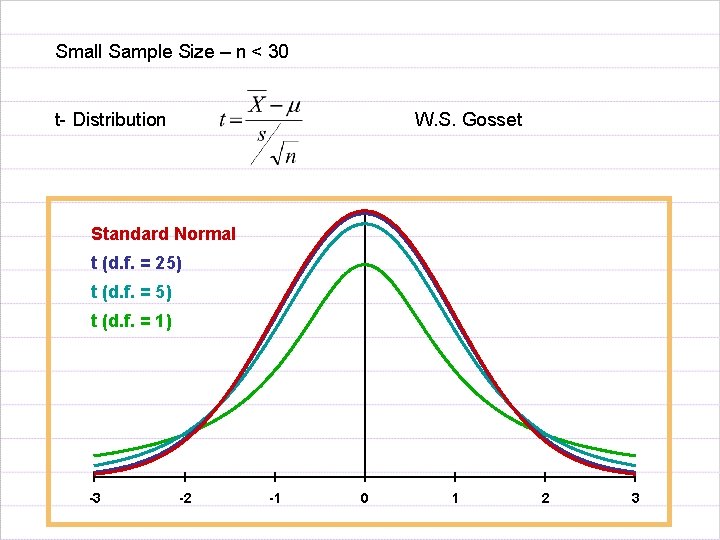
Small Sample Size – n < 30 t- Distribution W. S. Gosset Standard Normal t (d. f. = 25) t (d. f. = 1) -3 -2 -1 0 1 2 3

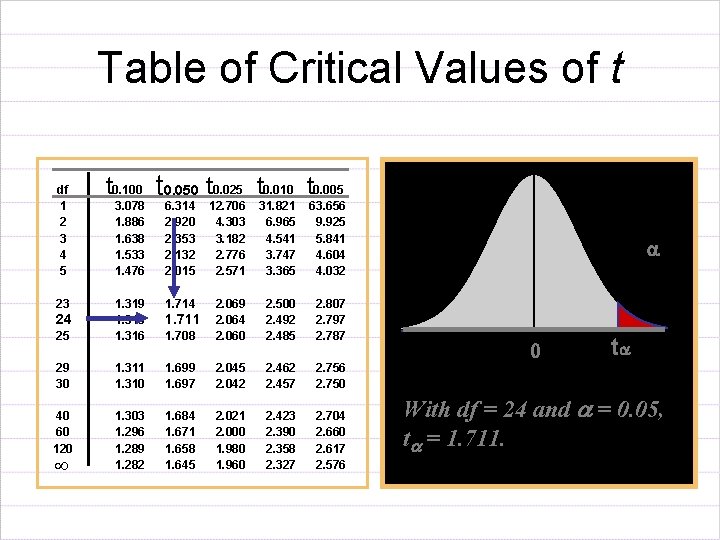
Table of Critical Values of t df 1 2 3 4 5 t 0. 100 t 0. 050 t 0. 025 t 0. 010 t 0. 005 3. 078 1. 886 1. 638 1. 533 1. 476 6. 314 2. 920 2. 353 2. 132 2. 015 12. 706 4. 303 3. 182 2. 776 2. 571 31. 821 6. 965 4. 541 3. 747 3. 365 63. 656 9. 925 5. 841 4. 604 4. 032 1. 714 25 1. 319 1. 318 1. 316 1. 708 2. 069 2. 064 2. 060 2. 500 2. 492 2. 485 2. 807 2. 797 2. 787 29 30 1. 311 1. 310 1. 699 1. 697 2. 045 2. 042 2. 462 2. 457 2. 756 2. 750 40 60 120 1. 303 1. 296 1. 289 1. 282 1. 684 1. 671 1. 658 1. 645 2. 021 2. 000 1. 980 1. 960 2. 423 2. 390 2. 358 2. 327 2. 704 2. 660 2. 617 2. 576 23 24 1. 711 t With df = 24 and a = 0. 05, ta = 1. 711.

Confidence Interval – X-e≤ µ ≤ X+e Ex: n =16, X = 20. 6 yr, s = 3 yr, C =. 95 Sample Size Calculation for Small Sample Problem?

Estimation of the Population Proportion n = sample size x = number with attribute = x/n Sample Proportion Estimator Unbiased? Standard Error for Estimator?

Confidence Interval for the Population Proportion

Ex: Percentage who plan to buy a new Car; n = 250, x = 80, C = 95 Ex: Percentage of Voters who will vote for Candidate; n = 400, x = 186, C =. 90

Sample Size Calculation - Ex: Voter poll e =. 01, C=. 95, p =. 50

Distribution of the Standard Error for Sample Proportion Ex: Sample Size to Estimate the Proportion Left-Handed

Finite Population Correction Ex: N = 5, 000, e =. 03, p =. 30, C =. 95