Statistical Analysis of the Nonequivalent Groups Design Analysis

Statistical Analysis of the Nonequivalent Groups Design

Analysis Requirements N N l l l O O X O O Pre-post Two-group Treatment-control (dummy-code)

Analysis of Covariance where: yi 0 1 2 Xi Zi ei y i = 0 + 1 X i + 2 Z i + e i = outcome score for the ith unit = coefficient for the intercept = pretest coefficient = mean difference for treatment = covariate = dummy variable for treatment(0 = control, 1= treatment) = residual for the ith unit

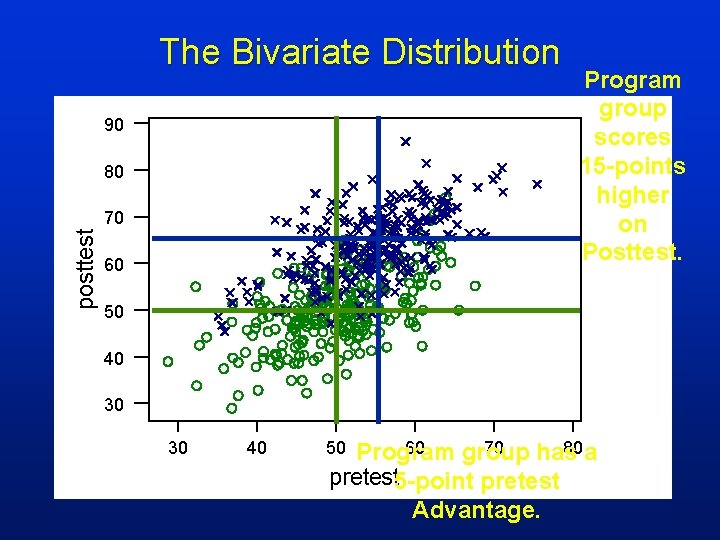
The Bivariate Distribution 90 80 posttest 70 60 Program group scores 15 -points higher on Posttest. 50 40 30 30 40 50 60 70 80 a Program group has pretest 5 -point pretest Advantage.

Regression Results yi = 18. 7 +. 626 Xi + 11. 3 Zi Predictor Coef Constant 18. 714 pretest 0. 62600 Group 11. 2818 l l l St. Err 1. 969 0. 03864 0. 5682 t 9. 50 16. 20 19. 85 Result is biased! CI. 95( 2=10) = 2± 2 SE( 2) = 11. 2818± 2(. 5682) = 11. 2818± 1. 1364 CI = 10. 1454 to 12. 4182 p 0. 000

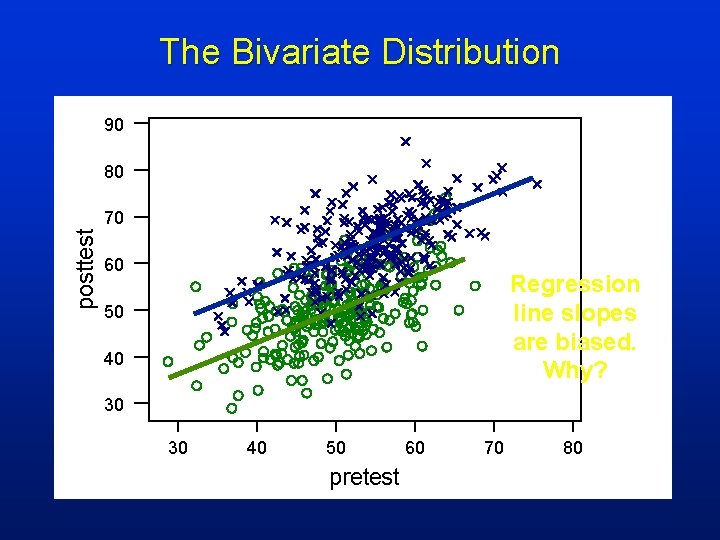
The Bivariate Distribution 90 80 posttest 70 60 Regression line slopes are biased. Why? 50 40 30 30 40 50 pretest 60 70 80

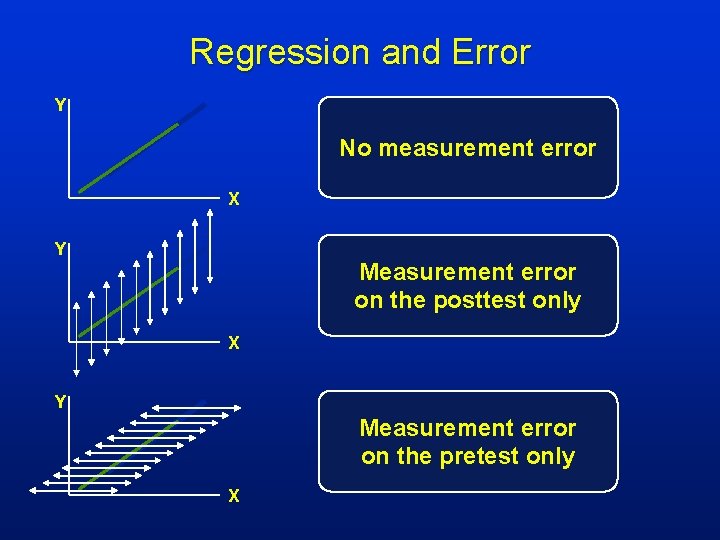
Regression and Error Y No measurement error X

Regression and Error Y No measurement error X Y Measurement error on the posttest only X

Regression and Error Y No measurement error X Y Measurement error on the posttest only X Y Measurement error on the pretest only X

How Regression Fits Lines

How Regression Fits Lines Method of least squares

How Regression Fits Lines Method of least squares Minimize the sum of the squares of the residuals from the regression line.

How Regression Fits Lines Method of least squares Minimize the sum of the squares of the residuals from the regression line. Y Least squares minimizes on y not x. X

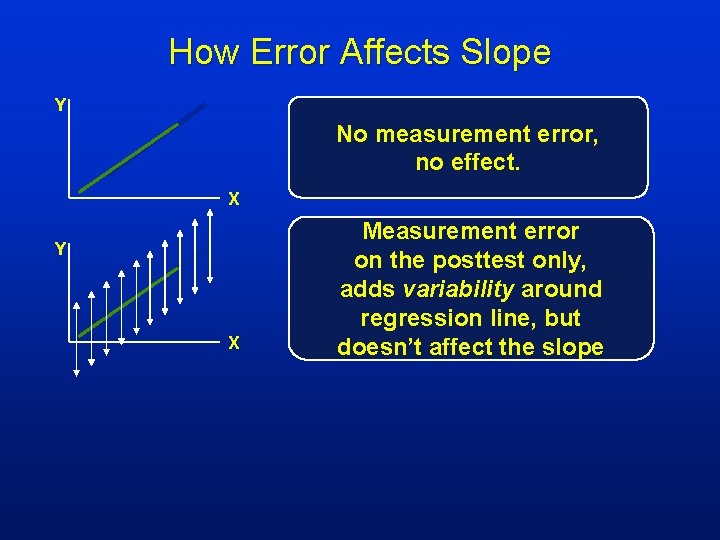
How Error Affects Slope Y No measurement error, No effect X

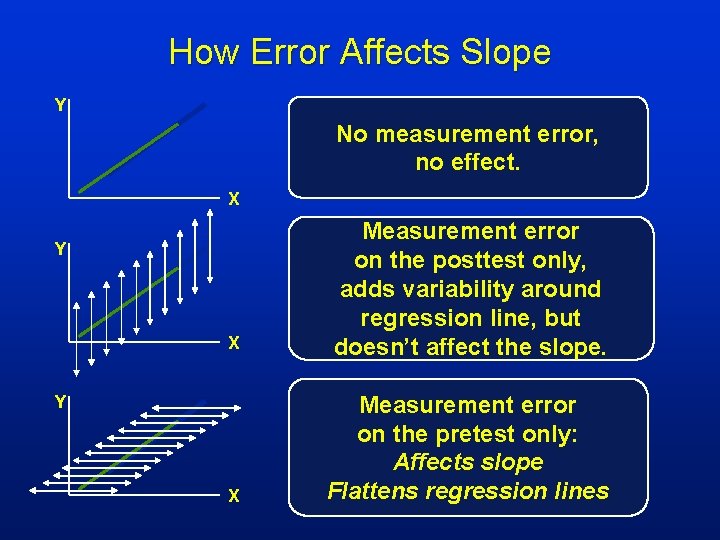
How Error Affects Slope Y No measurement error, no effect. X Y X Measurement error on the posttest only, adds variability around regression line, but doesn’t affect the slope

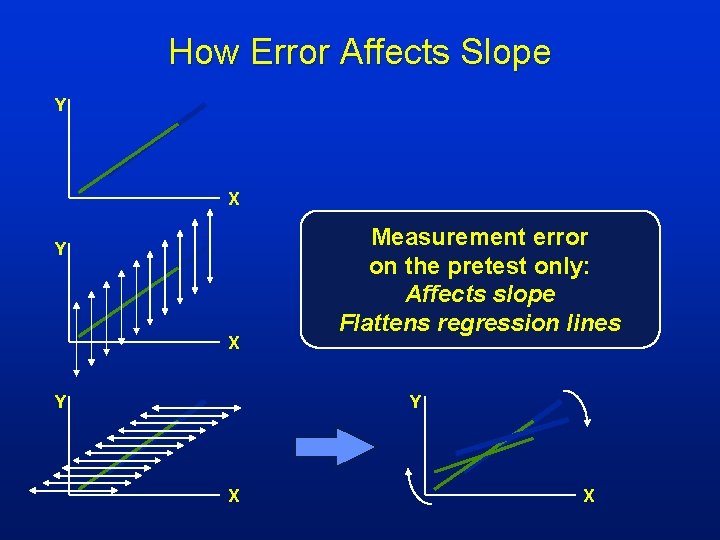
How Error Affects Slope Y No measurement error, no effect. X X Measurement error on the posttest only, adds variability around regression line, but doesn’t affect the slope. X Measurement error on the pretest only: Affects slope Flattens regression lines Y Y

How Error Affects Slope Y X Y Measurement error on the pretest only: Affects slope Flattens regression lines Y X X

How Error Affects Slope Y X Notice that the true result in all three cases should be a null (no effect) one. Y X Y Y X X

How Error Affects Slope Notice that the true result in all three cases should be a null (no effect) one. Null case Y X

How Error Affects Slope But with measurement error on the pretest, we get a pseudo-effect. Y Pseudo-effect X

Where Does This Leave Us? l l l Traditional ANCOVA looks like it should work on NEGD, but it’s biased. The bias results from the effect of pretest measurement error under the least squares criterion. Slopes are flattened or “attenuated”.

What’s the Answer? l l If it’s a pretest problem, let’s fix the pretest. If we could remove the error from the pretest, it would fix the problem. Can we adjust pretest scores for error? What do we know about error?

What’s the Answer? l l l We know that if we had no error, reliability = 1; all error, reliability=0. Reliability estimates the proportion of true score. Unreliability=1 -Reliability. This is the proportion of error! Use this to adjust pretest.

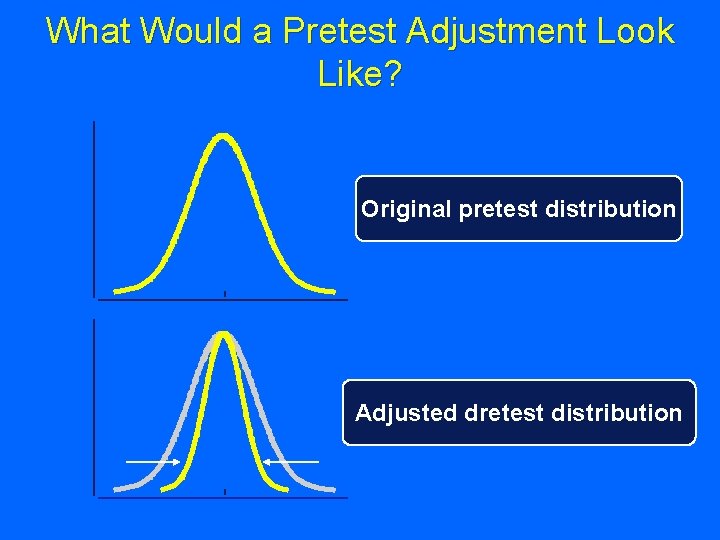
What Would a Pretest Adjustment Look Like? Original pretest distribution

What Would a Pretest Adjustment Look Like? Original pretest distribution Adjusted dretest distribution

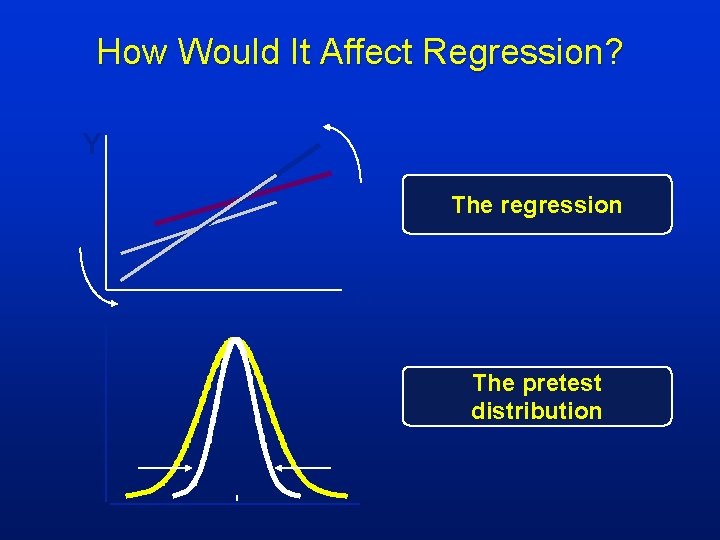
How Would It Affect Regression? Y The regression X The pretest distribution

How Would It Affect Regression? Y The regression X The pretest distribution

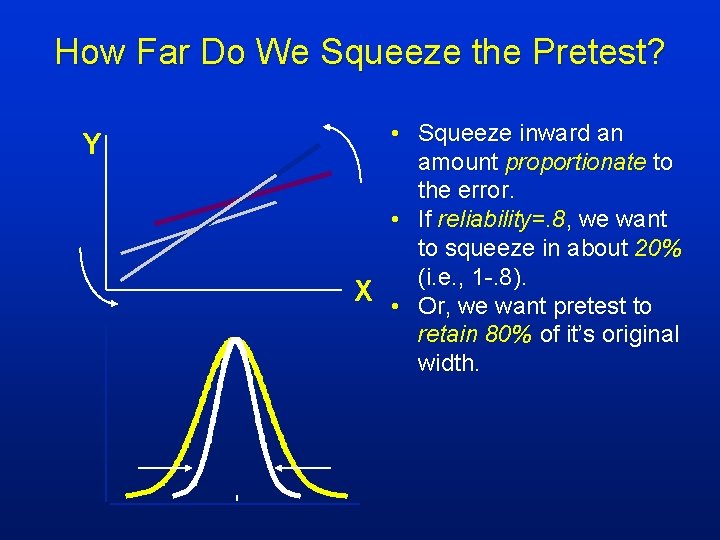
How Far Do We Squeeze the Pretest? Y • Squeeze inward an amount proportionate to the error. • If reliability=. 8, we want to squeeze in about 20% (i. e. , 1 -. 8). X • Or, we want pretest to retain 80% of it’s original width.

Adjusting the Pretest for Unreliability _ _ Xadj = X + r(X - X)

Adjusting the Pretest for Unreliability _ _ Xadj = X + r(X - X) where:

Adjusting the Pretest for Unreliability _ _ Xadj = X + r(X - X) where: Xadj = adjusted pretest value

Adjusting the Pretest for Unreliability _ _ Xadj = X + r(X - X) where: Xadj = _ X = adjusted pretest value original pretest value

Adjusting the Pretest for Unreliability _ _ Xadj = X + r(X - X) where: Xadj = _ X = adjusted pretest value r reliability = original pretest value

Reliability-Corrected Analysis of Covariance where: yi 0 1 2 Xadj Zi ei yi = 0 + 1 Xadj + 2 Zi + ei = outcome score for the ith unit = coefficient for the intercept = pretest coefficient = mean difference for treatment = covariate adjusted for unreliability = dummy variable for treatment(0 = control, 1= treatment) = residual for the ith unit

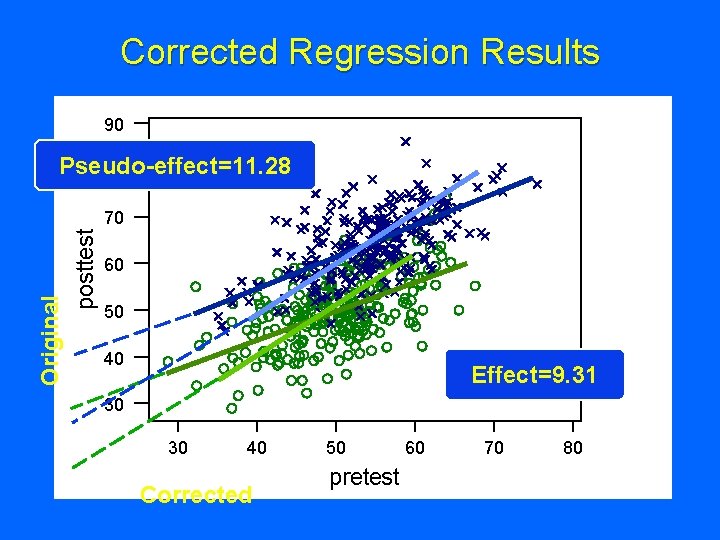
Regression Results yi = -3. 14 + 1. 06 Xadj + 9. 30 Zi Predictor Coef Constant -3. 141 adjpre 1. 06316 Group 9. 3048 l l l St. Err 3. 300 0. 06557 0. 6166 t -0. 95 16. 21 15. 09 Result is unbiased! CI. 95( 2=10) = 2± 2 SE( 2) = 9. 3048± 2(. 6166) = 9. 3048± 1. 2332 CI = 8. 0716 to 10. 5380 p 0. 342 0. 000

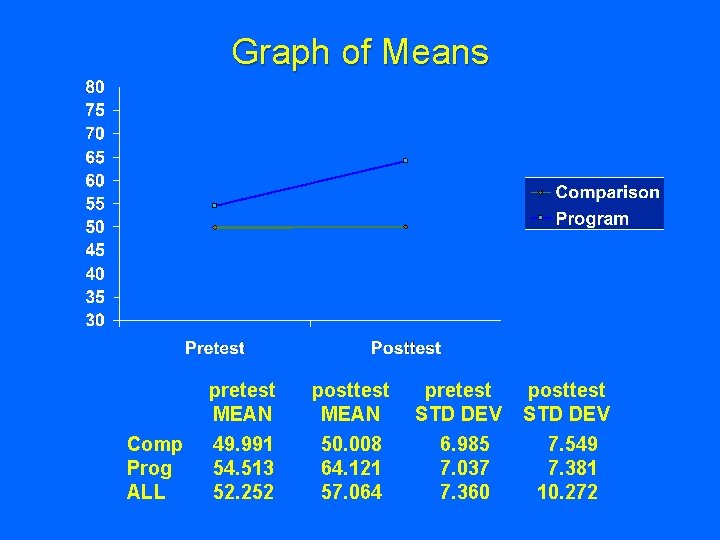
Graph of Means Comp Prog ALL pretest MEAN posttest MEAN 49. 991 54. 513 52. 252 50. 008 64. 121 57. 064 pretest STD DEV 6. 985 7. 037 7. 360 posttest STD DEV 7. 549 7. 381 10. 272

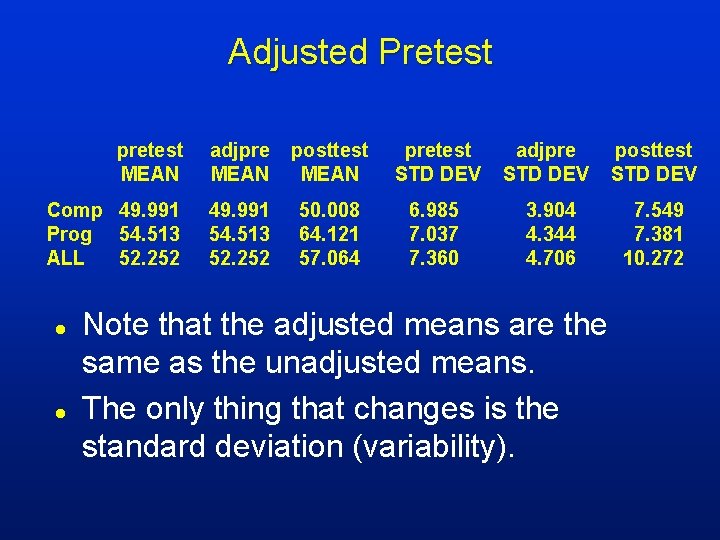
Adjusted Pretest pretest MEAN adjpre MEAN posttest MEAN pretest STD DEV adjpre STD DEV posttest STD DEV Comp 49. 991 Prog 54. 513 ALL 52. 252 49. 991 54. 513 52. 252 50. 008 64. 121 57. 064 6. 985 7. 037 7. 360 3. 904 4. 344 4. 706 7. 549 7. 381 10. 272 l l Note that the adjusted means are the same as the unadjusted means. The only thing that changes is the standard deviation (variability).

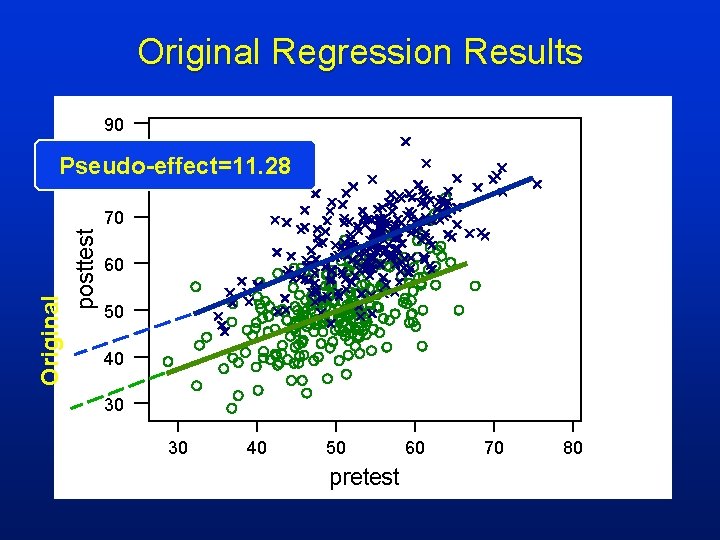
Original Regression Results 90 Pseudo-effect=11. 28 80 Original posttest 70 60 50 40 30 30 40 50 pretest 60 70 80

Corrected Regression Results 90 Pseudo-effect=11. 28 80 Original posttest 70 60 50 40 Effect=9. 31 30 30 40 Corrected 50 pretest 60 70 80