STATISTICAL ANALYSIS FOR ORIGINDESTINATION MATRICES OF TRANSPORT NETWORK

STATISTICAL ANALYSIS FOR ORIGIN-DESTINATION MATRICES OF TRANSPORT NETWORK Baibing Li Business School Loughborough University Loughborough, LE 11 3 TU

Overview STATISTICAL ANALYSIS FOR ORIGIN-DESTINATION MATRICES OF TRANSPORT NETWORKS l Background l Statement of the problem l Existing methods l Bayesian analysis via the EM algorithm l A numerical example l Conclusions

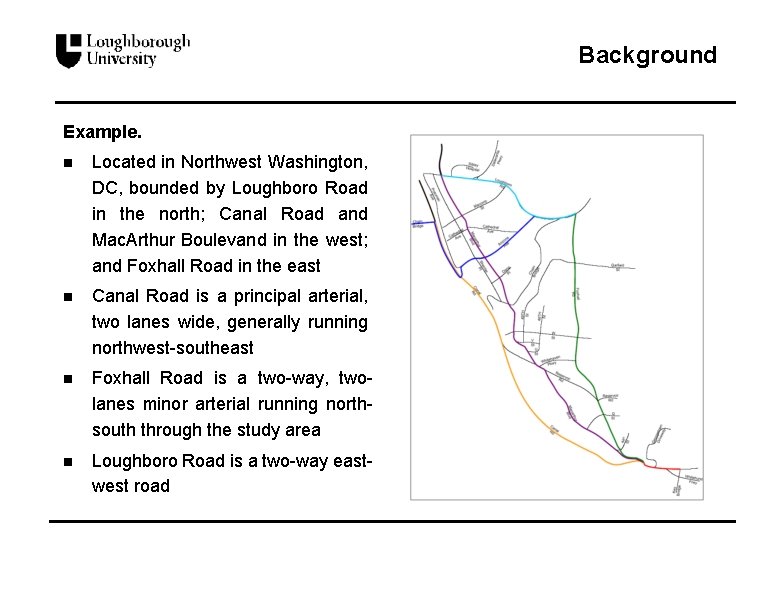
Background Example. n Located in Northwest Washington, DC, bounded by Loughboro Road in the north; Canal Road and Mac. Arthur Boulevand in the west; and Foxhall Road in the east n Canal Road is a principal arterial, two lanes wide, generally running northwest-southeast n Foxhall Road is a two-way, twolanes minor arterial running northsouth through the study area n Loughboro Road is a two-way eastwest road

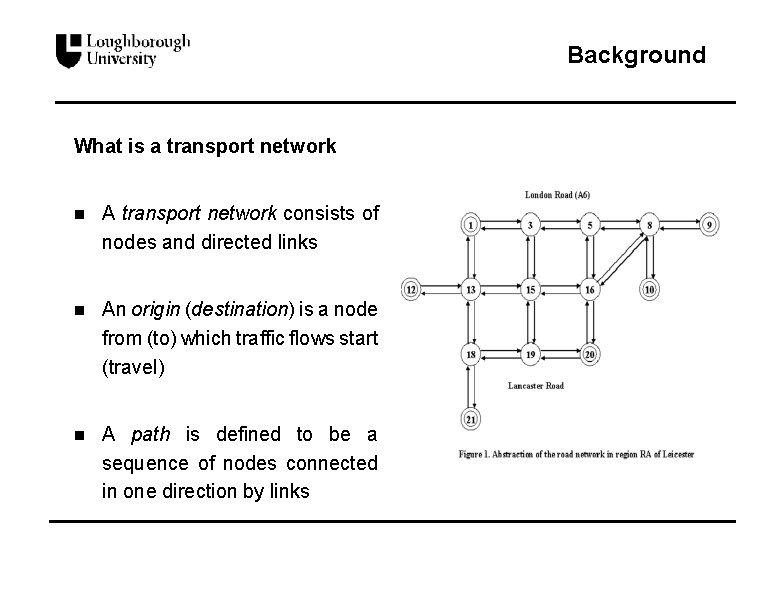
Background What is a transport network n A transport network consists of nodes and directed links n An origin (destination) is a node from (to) which traffic flows start (travel) n A path is defined to be a sequence of nodes connected in one direction by links

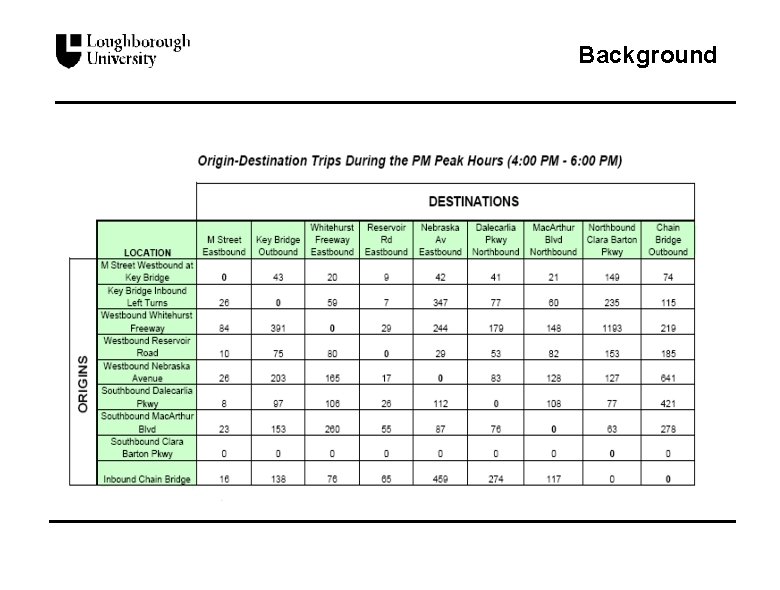
Background n Origin-destination (O-D) matrices l An O-D matrix consists of traffic counts from all origins to all destinations l It describes the basic pattern of demand across a network l It provides fundamental information for transport management

Background

Background n Methods of obtaining O-D data l Roadside interviews and roadside mailback questionnaires disruption of traffic flow; unpopular with drivers and highway authorities l Registration plate matching very susceptible to error (e. g. a vehicle passing two observation points has its plate incorrectly recorded at one of the points) l Use of vantage point observers or video for small study area (e. g. to determine the pattern of flows through a complex intersection) l Traffic counts much cheaper than surveys; much smaller observation errors

Statement of the problem n Statement of the problem l Aim: Inference about O-D matrices l Available data: traffic counts A relatively inexpensive method is to collect a single observation of traffic counts on a specific set of network links over a given period

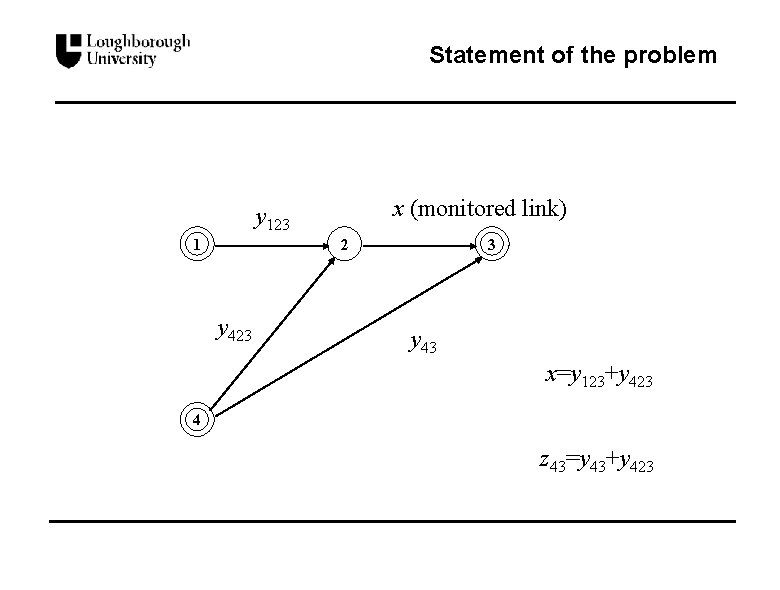
Statement of the problem n Notation l y=[y 1, …, yc]T is the vector of the traffic counts on all feasible paths (ordered in some arbitrary fashion) l x=[x 1, …, xm]T is the vector of the observed traffic counts on the monitored links. z=[z 1, …, zn]T be the vector of O-D traffic counts l l l The matrix A is an m c path-link incidence matrix for the monitored links only, whose (i, j)th element is 1 if link i forms part of path j; otherwise 0 The matrix B is an n c matrix whose (i, j)th element is 1 if path j connects O-D pair i; otherwise 0

Statement of the problem n Statistical model (I) x = Ay z = By l Assume that y 1, …, yc are unobserved independent Poisson random variables with means 1, …, c respectively, i. e. yi ~ Poisson(yi; i). Denote =[ 1, …, c]T l Vector x has a multivariate Poisson distribution with a mean of A

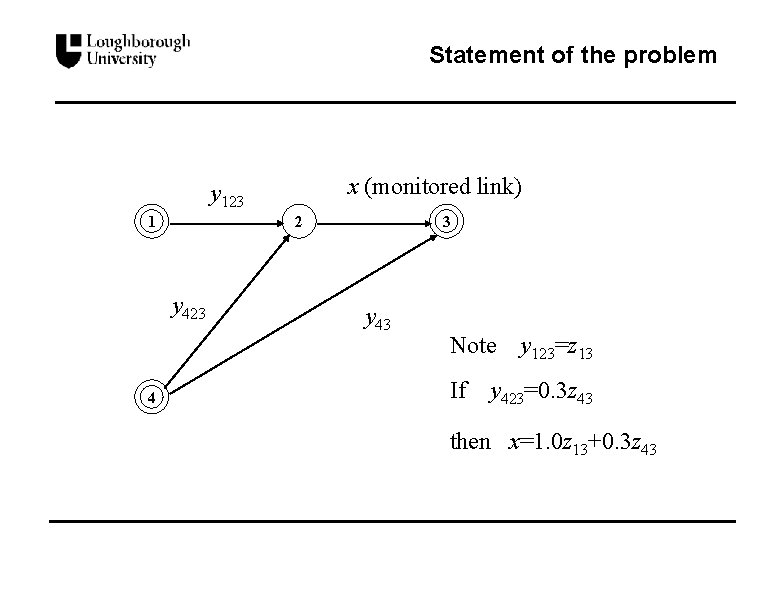
Statement of the problem x (monitored link) y 123 1 3 2 y 423 y 43 x=y 123+y 423 4 z 43=y 43+y 423

Statement of the problem n Statistical model (II) x = Pz l P*= [pij] is a proportional assignment matrix, where pij is defined to be the proportions of using link j which connects O-D pair i (assumed to be available). P is a sub-matrix of selecting those rows associated with x l A common assumption is that the O-D counts zj are independent Poisson variates, thus x being linear combinations of the Poisson variates with mean of P , where is the mean of z

Statement of the problem x (monitored link) y 123 1 y 423 4 3 2 y 43 Note If y 123=z 13 y 423=0. 3 z 43 then x=1. 0 z 13+0. 3 z 43

Statement of the problem n Relationship between Model (I) and Model (II) Assumptions: l O-D traffic counts zj are independent Poisson random variables with mean j l If yj =[yjk] is vector of route flows and pj=[pjk] route probabilities for O-D pair j, then conditional upon the total number of O-D trips, then yj ~ multinomial(zj, pj) Conclusion: l The distributions of yjk are Poisson with parameters jk = jpjk

Statement of the problem n Major research challenges l A highly underspecified problem for inference about an O-D matrix from a single observation l An analytically intractable likelihood

Statement of the problem n Example of multivariate Poisson distributions l Let Y 1, Y 2, and Y 3 be three independent Poisson variates Yi ~ Poisson(yi; i) l Define X 1= Y 1+Y 3 and X 2= Y 2+Y 3. The joint distribution of X 1 and X 2 is a multivariate Poisson distribution:

Previous research n Maximum entropy method (Van Zuylen and Willumsen, 1980) --- Dealing with the issue of under-specification l Maximising entropy, subject to the observation equations l Adding as little information as possible to the knowledge contained in the observation equations

Previous research n Using normal approximations (Hazelton, 2001) --- Dealing with intractability of multivariate Poisson distributions To circumvent the problem, Hazelton (2001) considered following multivariate normal approximation for the distribution of y: Since x = Ay, we obtain Note that the covariance matrix depends on .

Bayesian analysis + EM algorithm n Basic idea --- dealing with the issue of intractability Instead of an analysis on the basis of the observed traffic counts x, the inference will be drawn based on unobserved y l l Incomplete data u The observed network link traffic counts x are treated as incomplete data (observable) u Follow a multivariate Poisson --- analytically intractable Complete data u The traffic counts on all feasible paths, y, are treated as complete data (unobservable) u Follow a univariate Poisson --- analytically tractable

Bayesian analysis + EM algorithm n Basic idea --- dealing with the issue of under-specification Bayesian analysis combines two sources of information l Prior knowledge e. g. an obsolete O-D matrix; or non-informative prior in the case of no prior information l Current observation on traffic flows

Bayesian analysis n Complete-data Bayesian inference l Complete-data likelihood P(y | ) The joint distribution of y: l ∏j Poisson(yj | j ) Incorporate a natural conjugate prior ( ) j ~ Gamma ( j; j) l Result in a posterior density P( | y ) j ~ Gamma (aj; bj) with aj= j+ yj and bj= j+1

The EM algorithm n n Posterior density l Prior density ( ) l Complete-data likelihood P(y | )=P(x | )P(y | x, ) l Complete-data posterior density P( | y ) P(y | ) ( ) E-step: averaging over the conditional distribution of y given (x, (t)) E{log. P( | y ) | x, (t) }=l( | x)+E{log. P(y | x, ) | x, (t) }+log ( (t))+c n M-step: choosing the next iterate (t+1) to maximize E{log. P( | y ) | x, (t) } Each iteration will increase l( | x) and { (t)} will converge

The EM algorithm n Bayesian inference via the EM algorithm l M-step The a posteriori most probable estimate of j is given by ( j+ yj 1)/( j+1) l E-step Replacing the unobservable data yj by its conditional expectation at the t-th iteration: ( j+ E{yj | x, (t)} 1)/( j+1)

Conditional expectation n Calculation of conditional expectation l Theorem. Suppose that {yj} are independent Poisson random variables with means { j} (j=1, …, c) and A=[A 1, , Ac] is an m c matrix with Aj the jth column of A. Then for a given m 1 vector, x, we have E{yj | x, (t)}= j(t) {Pr(Ay=x Aj) /Pr(Ay=x)} Major advantage: guarantee positivity

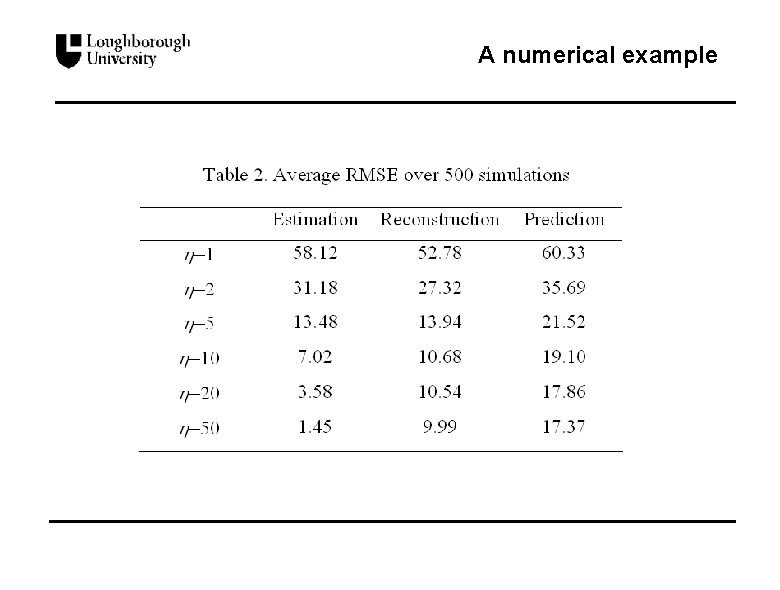
Estimation, prediction & reconstruction n Hazelton (2001) has investigated some fundamental issues and clarified some confusion in the inference for O-D matrices. He clearly defines the following concepts: l Estimation The aim is to estimate the expected number of O-D trips l Prediction The aim is to estimate future O-D traffic flows l Reconstruction The aim is to estimate the actual number of trips between each O-D pair that occurred during the observational period

Prediction n For future traffic counts, the complete-data posterior predictive distribution is n The complete-data marginal posterior predictive distributions are negative binomial distributions with n The mode of the marginal posterior predictive distribution is at n Given the incomplete data x, the prediction is

Reconstruction n The marginal distributions of yj are NB( j , j ). Denote the corresponding probability mass functions as n For given observation x, the reconstructed traffic counts can be calculated as the a posteriori most probable vector of y, i. e. the solution to the following maximization problem: subject to Ay=x n Solving the above problem yields the reconstructed traffic counts

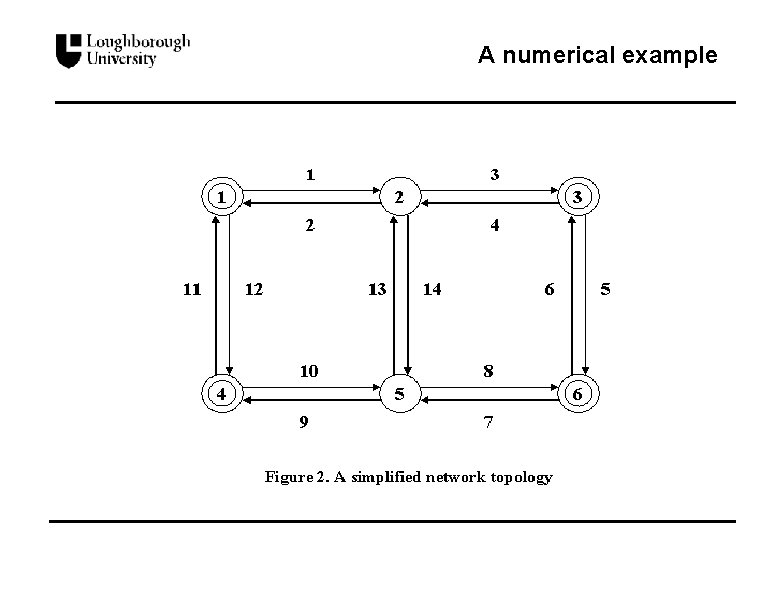
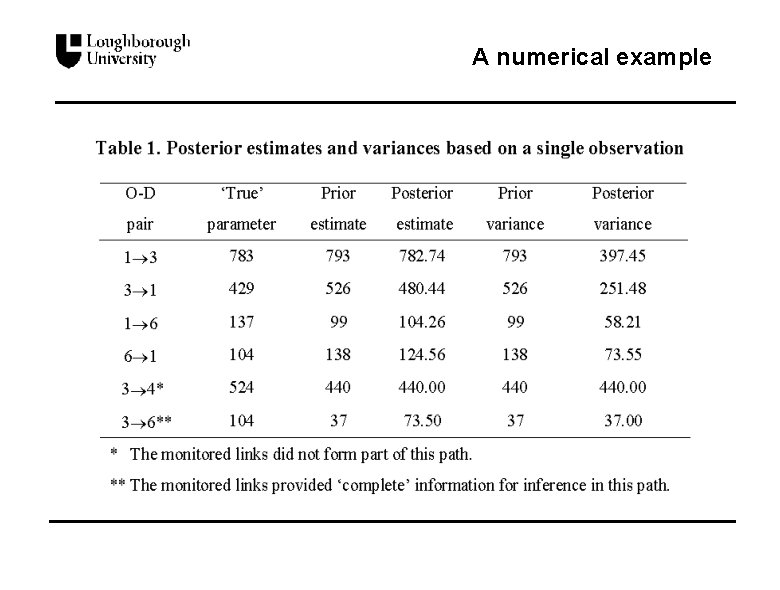
A numerical example

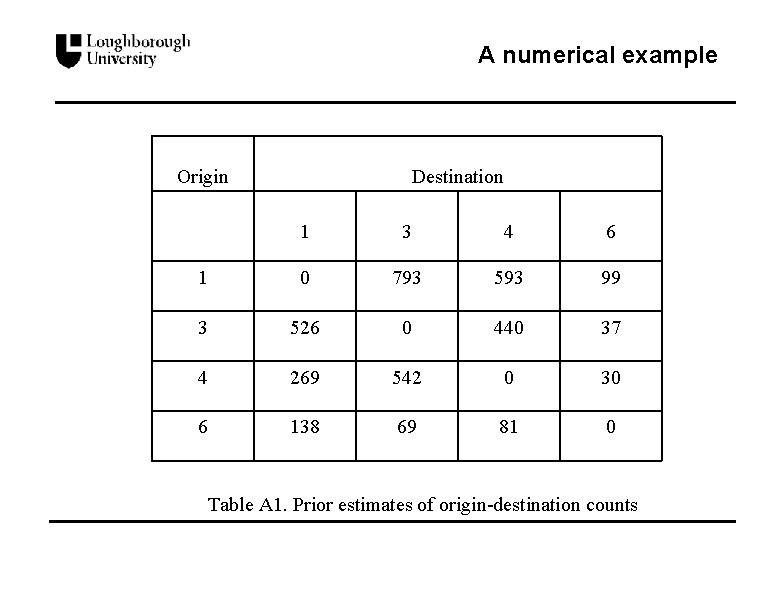
A numerical example Origin Destination 1 3 4 6 1 0 793 593 99 3 526 0 440 37 4 269 542 0 30 6 138 69 81 0 Table A 1. Prior estimates of origin-destination counts

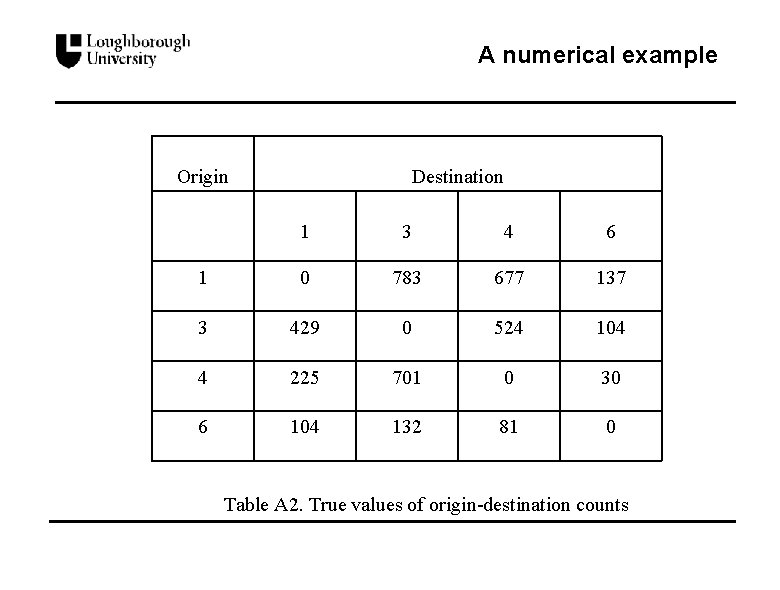
A numerical example Origin Destination 1 3 4 6 1 0 783 677 137 3 429 0 524 104 4 225 701 0 30 6 104 132 81 0 Table A 2. True values of origin-destination counts

A numerical example n Prior distributions The prior distributions are taken as Gamma distributions with parameters j being the prior estimates in Table A 1 and j =1 n Simulated data l Simulation of unobservable vector of traffic counts, y outcomes of independent Poisson variables with means displayed in Table A 2. l Monitored links Assume the traffic counts are available on m=8 of the links, i. e. links 1, 2, 5, 6, 7, 8, 11, 12. l Simulation of a single observation, x=Ay x = [884, 548, 111, 133, 191, 144, 214, 640]T.

A numerical example

A numerical example n Repeated experiments l The simulation experiment was repeated 500 times l The quality of prior information varies via adjusting the parameters of the prior distributions ( j; j) with = 1, 2, 5, 10, 20 , 50 l j* are the ‘true’ values of the parameters in Table A 2 and j 0 are the prior values in Table A 1

A numerical example

Conclusions n n Bayesian analysis l Challenge: a highly underspecified problem for inference about an O-D matrix from a single observation l Solution: Bayesian analysis combining the prior information with current observation The EM algorithm l Challenge: an analytically intractable likelihood of observed data l Solution: the EM algorithm dealing with unobservable complete data which have analytically tractable likelihood

References Hazelton, L. M. (2001). Inference for origin-destination matrices: estimation, prediction and reconstruction. Transportation Research, 35 B, 667 -676. Li, B. (2005). Bayesian inference for origin-destination matrices of transport networks using the EM algorithm. Technometrics, 47, 2005, 399 -408. Van Zuylen, H. J. and Willumsen, L. G. (1980). The most likely trip matrix estimated from traffic counts. Transportation Research, 14 B, 281 -293.