Statistical Analysis Biomedical Innovations 2015 Project Lead The

Statistical Analysis Biomedical Innovations © 2015 Project Lead The Way, Inc.

Purpose of Statistical Analysis • Determines whether the results found in an experiment are meaningful. • Answers the question: Does the experimental data support the research hypothesis? Biomedical Innovations

Example Study A researcher performs a clinical trial to determine whether a new medication is effective in lowering LDL cholesterol levels in patients with hypercholesterolemia. Study hypothesis: The experimental medication will be more effective in lowering LDL cholesterol levels than the placebo. Biomedical Innovations

Initial Results Upon conducting the experiment, the investigator found that the mean cholesterol levels of the group that experimental drug was lower than those who received the placebo. Is this information enough to conclude that the drug is more effective than the placebo? NO Biomedical Innovations

Getting Started How could this researcher use statistics to further analyze the data for this study? Biomedical Innovations

Statistical Testing There are several types of statistical tests to analyze data. For this study, we will use a two sample t-test. Two sample t-test: Used to determine whether the differences between the means of two populations are statistically significant. Biomedical Innovations

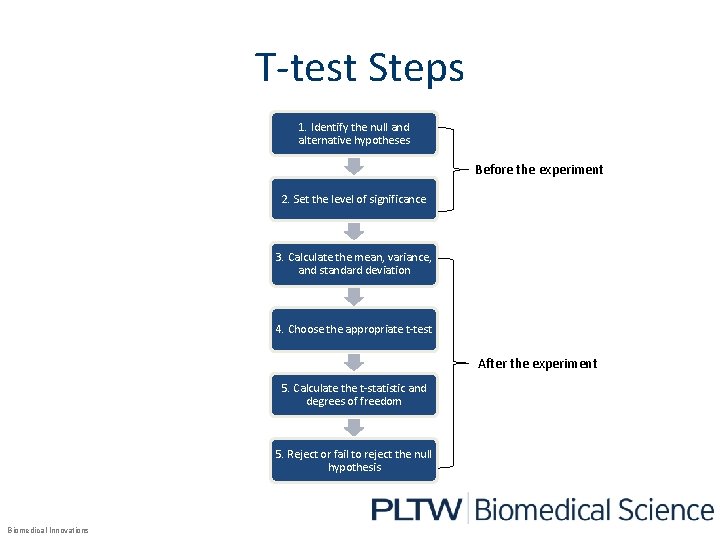
T-test Steps 1. Identify the null and alternative hypotheses Before the experiment 2. Set the level of significance 3. Calculate the mean, variance, and standard deviation 4. Choose the appropriate t-test After the experiment 5. Calculate the t-statistic and degrees of freedom 5. Reject or fail to reject the null hypothesis Biomedical Innovations

Two Sample T-test Steps 1. Identify the null and alternative hypotheses 2. Set the level of significance 3. Calculate the mean, variance, and standard deviation 4. Choose the appropriate t-test 5. Calculate the t-statistic and degrees of freedom 6. Reject or fail to reject the null hypothesis Biomedical Innovations

Step 1: Identify the Hypotheses When using statistics to analyze data, it is necessary to set up two hypotheses. 1. Null hypothesis 2. Alternative hypothesis Note: Both hypotheses should be set up before beginning the experiment. Biomedical Innovations

Null Hypothesis (H 0): The starting point in scientific research where the investigator assumes there is no effect of the treatment or no relationship between two variables. The null hypothesis variables are typically set as an equality. • Example: The mean of group one (µ 1) is equal to the mean of group two (µ 2). µ 1= µ 2 Biomedical Innovations

Alternative Hypothesis (Ha): Known as the research hypothesis, it is what the investigator believes to be true. The means are typically set as an inequality, meaning that they are not equal. • There are two types of alternative hypotheses: directional and nondirectional. Biomedical Innovations

Types of Alternative Hypothesis 1. Directional Alternative Hypothesis: Prediction that the mean (µ) of group one (µ 1) will be more than or less than the mean of group 2 (µ 2). • Example Ha: µ 1>µ 2 or µ 1<µ 2 2. Nondirectional Alternative Hypothesis: Prediction that the mean of group one is not equal to the mean of group two. • Biomedical Innovations Example Ha: µ 1≠µ 2

LDL Experimental Study • Recall that there are two groups, 4 patients in each group, being studied. – Group 1 received the experimental drug and their mean cholesterol is represented by µD. – Group 2 received the placebo drug and their mean cholesterol is represented by µP. • What should the investigator use for the null and alternative hypothesis? Biomedical Innovations © 2013 Project Lead The Way, Inc.

Hypotheses for the LDL Medication Experiment • Null Hypothesis: There is no difference in LDL cholesterol levels in patients given the medication (µD) than in patients given the placebo (µP). Ho: µD= µP • Alternative Hypothesis: The LDL cholesterol levels will be lower in the patients given the medication than the patients given the placebo. Ha: µD< µP Biomedical Innovations

Two Sample T-test Steps 1. Identify the null and alternative hypothesis 2. Set the level of significance 3. Calculate the mean, variance, and standard deviation 4. Choose the appropriate t-test 5. Calculate the t-statistic and degrees of freedom 6. Reject of fail to reject the null hypothesis Biomedical Innovations

Step 2: Set the Level of Significance • The level of significance, alpha (α), must be set prior to the investigation. • α is used to determine the percentage of results that will occur due to chance. – The lower the alpha value, the higher probability that an experiment will have the similar results. This is know as the degree of reliability. o Degree of reliability=(1 - α) x 100 o Ex: An experiment α=0. 05 has 95% degree of reliability • Typical α values: 0. 01, 0. 05, or 0. 10. • α is also be used to determine if the null hypothesis should be rejected. Biomedical Innovations

Level of Significance for the LDL Medication Experiment For the LDL example study we will assume that α is 0. 05, which has a 95% chance that results will be the similar if this investigation is repeated many times. Now the investigator will conduct the study and collect data that will be analyzed for the remainder of the steps. Biomedical Innovations

Two Sample T-test Steps 1. Identify the null and alternative hypothesis 2. Set the level of significance 3. Calculate the mean, variance, and standard deviation 4. Choose the appropriate t-test 5. Calculate the t-statistic and degrees of freedom 6. Reject of fail to reject the null hypothesis Biomedical Innovations

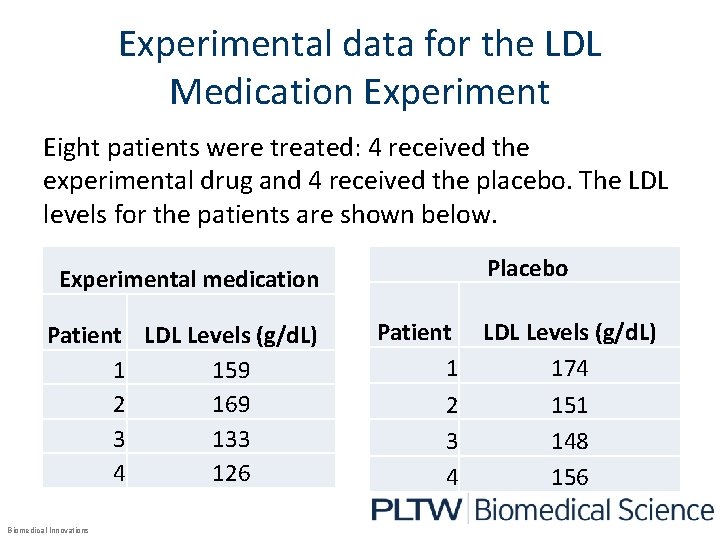
Experimental data for the LDL Medication Experiment Eight patients were treated: 4 received the experimental drug and 4 received the placebo. The LDL levels for the patients are shown below. Experimental medication Patient LDL Levels (g/d. L) 1 159 2 169 3 133 4 126 Biomedical Innovations Placebo Patient LDL Levels (g/d. L) 1 174 2 151 3 148 4 156

Step 3: Calculations • Determine what values are typical, or normal, for the data collected. • Calculate the mean, variance, and standard deviation. Biomedical Innovations

Mean • Biomedical Innovations

Mean Calculation for the LDL Data • Biomedical Innovations •

Variance (s 2): The measure of the spread of the data about the mean. The more spread out the data points are, the larger the variance. Calculating the variance: 2. Square these deviations. Biomedical Innovations 3. Calculate the sum of all of these squared deviations. 4. Divide by the number of data points in the data set minus one.

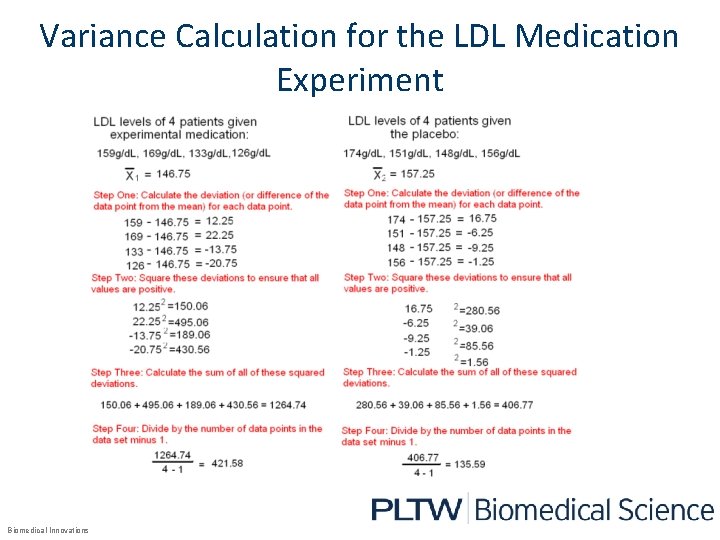
Variance Calculation for the LDL Medication Experiment Biomedical Innovations

Standard Deviation • 1. Calculate the variance for the data set. 2. Take the square root of the variance. Biomedical Innovations

Example Calculation for the LDL Medication Experiment • Biomedical Innovations •

What Do The Results Show? • The mean of the LDL levels of the subjects given the experimental medication were lower than subjects given the placebo. Patient Information Experimental Drug Placebo Mean LDL (g/d. L) 146. 75 157. 25 Variance 421. 58 135. 99 Standard deviation 20. 58 11. 64 Now the researcher will determine if the observed difference is statistically significant and caused by the medication and not chance using the two sample t-test. Biomedical Innovations

Two Sample T-test Steps 1. Identify the null and alternative hypothesis 2. Set the level of significance 3. Calculate the mean, variance, and standard deviation 4. Choose the appropriate t-test 5. Calculate the t-statistic and degrees of freedom 6. Reject or fail to reject the null hypothesis Biomedical Innovations

Step 4: Choosing the t-test • There are two main types of two sample ttests: – Independent – Dependent (paired t-test) • Each type has several variations that depend on the experimental conditions. Biomedical Innovations

Independent t-test Used to determine whether the difference between the means of two independent populations, that are being tested for the same dependent variable, is statistically significant. Example: Study where one group is given the experimental device and another group is given a placebo. Biomedical Innovations

Independent t-test Variation The formula used will depend on the number of samples (n) and if the two groups are of equal size. Equation 1 Biomedical Innovations Formula When to Use Sample sizes are unequal AND either one or both samples are small (n<30) 2 Sample sizes are equal (regardless of size) 3 Sample sizes are unequal AND both sample sizes are large (n>30)

Dependent t-test Used to determine whether the difference between the means of two groups, each containing the same participants and being tested at two different points, is statistically significant. Example: Study where the same group of participants is followed before and after an experimental treatment. Biomedical Innovations

Formula for Dependent t-test Type of t-test Dependent t-test Biomedical Innovations Formula When to Use with paired samples (i. e. , subjects pretest and posttest)

Now Back to the LDL Medication Experiment Determine which type of t-test (independent or dependent) is most appropriate for our LDL levels experiment. • Because the two groups being tested are independent of each other (participants in the experimental group and the control group are different), the independent t-test is the appropriate test to use. Biomedical Innovations

Which variation of the formula should we use? Both groups have four participants. Because the sample sizes are equal, the second variation should be used. Equation 1 2 3 Biomedical Innovations Formula When to Use Sample sizes are unequal AND either one or both samples are small (n<30) Sample sizes are equal (regardless of size) Sample sizes are unequal AND both sample sizes are large (n>30)

Two Sample T-test Steps 1. Identify the null and alternative hypothesis 2. Set the level of significance 3. Calculate the mean, variance, and standard deviation 4. Choose the appropriate t-test 5. Calculate the t-statistic and degrees of freedom 6. Reject or fail to reject the null hypothesis Biomedical Innovations

Step 5: Calculating the t-statistic • Biomedical Innovations

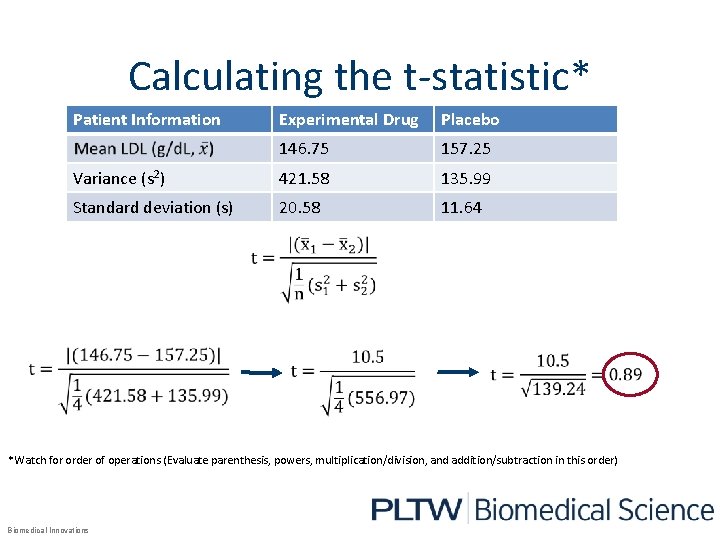
Calculating the t-statistic* Patient Information Experimental Drug Placebo 146. 75 157. 25 Variance (s 2) 421. 58 135. 99 Standard deviation (s) 20. 58 11. 64 *Watch for order of operations (Evaluate parenthesis, powers, multiplication/division, and addition/subtraction in this order) Biomedical Innovations

Degrees of Freedom Now that we know the t-statistic, the degrees of freedom must calculated. • Degrees of Freedom (ν): A measure of certainty that the sample populations are representative of the population being studied. Biomedical Innovations

Calculating Degree of Freedom The degrees of freedom calculation is determined by the chosen t-test. Type of t-test Formula When to Use Degrees of Freedom (v) n 1+n 2 -2 Independent t-test 1 Sample sizes are unequal AND either one or both samples are small (n<30) Independent t-test 2 Sample sizes are equal (regardless of size) n 1+n 2 -2 Independent t-test 3 Sample sizes are unequal AND both sample sizes are large (n>30) n 1+n 2 -2 Dependent t-test Use with paired samples (i. e. , subjects pretest and posttest) n-1 Biomedical Innovations

Degrees of Freedom for the LDL Medication Experiment • n 1=number of samples for group 1 n 1 =number of samples for group 2 Biomedical Innovations

You’re Not Done Yet • You just calculated the t-statistic and degrees of freedom. • We will move to the last step in which you will use a t-table in order to determine if you will reject or fail to reject the null hypothesis. Biomedical Innovations

Two Sample T-test Steps 1. Identify the null and alternative hypothesis 2. Set the level of significance 3. Calculate the mean, variance, and standard deviation 4. Choose the appropriate t-test 5. Calculate the t-statistic and degrees of freedom 6. Reject or fail to reject the null hypothesis Biomedical Innovations

Step 6: Completing the T-test For the last step of the two sample t-test you will determine whether to reject or fail to reject the null hypothesis. • Recall the two research hypotheses for the LDL study and their meanings. Hypothesis Statement Null Alternative Biomedical Innovations Meaning Ho: µD=µP The LDL levels of both groups will be equal. HA: µD<µP The LDL levels of the investigative drug group will be lower than the placebo.

How is the fate of the null hypothesis determined? Now that we calculated the t-statistic, we will use alpha and the degrees of freedom to find the critical value found in the T-table to determine the fate of the null hypothesis. • The critical value will be compared the calculated t-statistic from Step 5. Biomedical Innovations

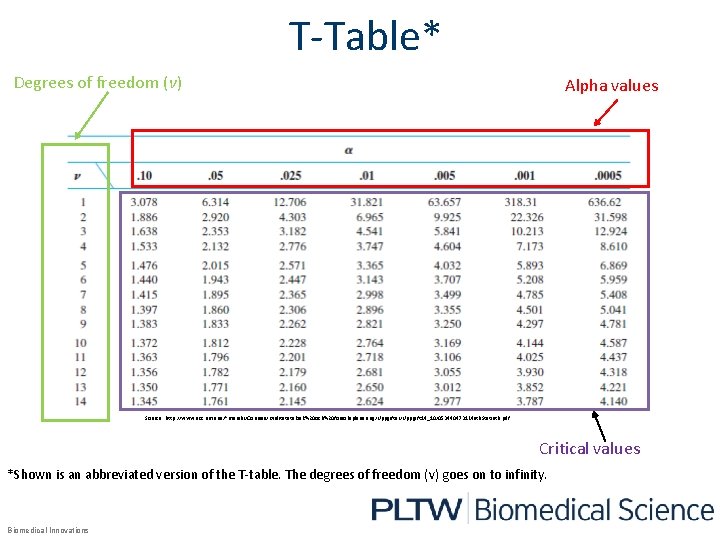
T-Table* Degrees of freedom (v) Alpha values Source: http: //www. acc. umu. se/~marshi/Courses/Kvalitetsteknik%20 och%20 forsoksplanering/Uppgifter/Uppgift 14_10/0534404731 Math. Statist. B. pdf Critical values *Shown is an abbreviated version of the T-table. The degrees of freedom (v) goes on to infinity. Biomedical Innovations

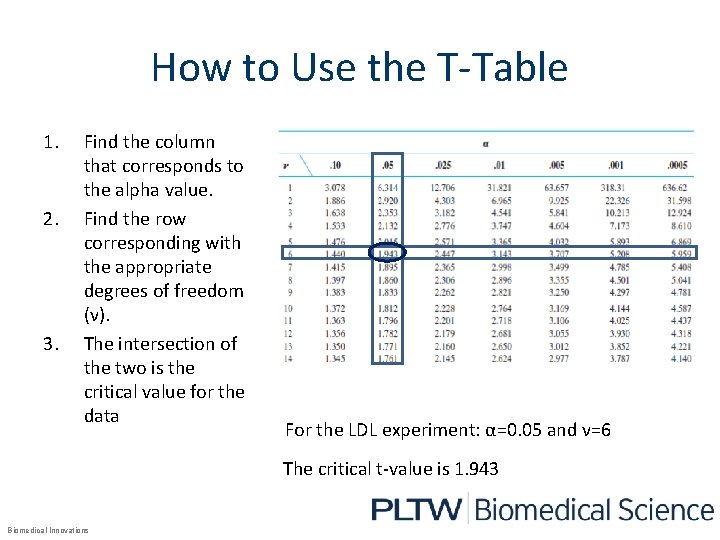
How to Use the T-Table 1. 2. 3. Find the column that corresponds to the alpha value. Find the row corresponding with the appropriate degrees of freedom (ν). The intersection of the two is the critical value for the data For the LDL experiment: α=0. 05 and ν=6 The critical t-value is 1. 943 Biomedical Innovations

Null Hypothesis Rejection Criteria Results are statistically significant t-statistic*> the critical value Reject the null hypothesis Rejection criteria t-statistic*< the critical value *use the absolute value of the t-statistic Fail to reject the null hypothesis Result are NOT statistically significant LDL Data: T-statistic=0. 89, Critical value from t-chart=1. 943 Since the t-statistic is less than the critical value, we fail to reject the null hypothesis. The results are NOT statistically significant, meaning there is no difference in the LDL levels for the two groups. The observed difference was due to chance. Biomedical Innovations

Research Study Debrief • Based on the t-test, the investigator can conclude that the results are NOT statistically significant. • This means that the new medication did NOT lower patients’ LDL levels more than the placebo. Biomedical Innovations

Summary • A two sample t-test is a statistical method that compares the means of two population samples. • The test can determine if the results are significant (a real difference and not due to chance). • The results can be determined to be not significant (the difference is due to chance). Biomedical Innovations

Thinking Further (Optional) Nondirectional Alternative Hypothesis Biomedical Innovations

What if I have a nondirectional alternative hypothesis? • Remember that if the means of the alternative hypothesis are not equal (≠), then it is a nondirectional hypothesis. • The LDL experiment had a directional alternative hypothesis (Ha: µD< µP) So if we had chosen Ha: µD≠ µP how would we solve the problem? Biomedical Innovations

One-Tailed vs. Two-Tailed Test for Significance • How does this impact α and the degrees of freedom? – Degrees of freedom: no impact • α values depends on the type of test – One tailed: α is unaffected – Two-tailed: Use α/2 for the α value Biomedical Innovations Alternative hypothesis Directional (µ 1>µ 2 or µ 1<µ 2) Nondirectional (µ 1≠µ 2) One-tailed test Two-tailed test

Using a Two-Tailed Test for Significance? Now let’s examine if we used the following hypotheses for the LDL experiment: Null hypothesis: Ho: µD= µP Alternative hypothesis: Ha: µD≠ µP Steps 1 -5 would yield the same results. Let’s start with the t -statistic is equal to 0. 89. Biomedical Innovations

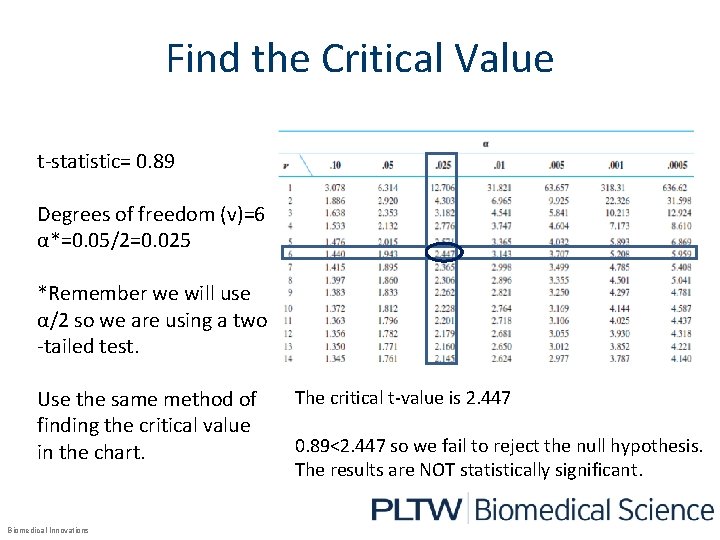
Find the Critical Value t-statistic= 0. 89 Degrees of freedom (v)=6 α*=0. 05/2=0. 025 *Remember we will use α/2 so we are using a two -tailed test. Use the same method of finding the critical value in the chart. Biomedical Innovations The critical t-value is 2. 447 0. 89<2. 447 so we fail to reject the null hypothesis. The results are NOT statistically significant.