Statistical Analyses ttests Psych 250 Winter 2013 Hypothesis

Statistical Analyses t-tests Psych 250 Winter, 2013

Hypothesis: People will give longer sentences when the victim is female.

Independent Variable: Gender of the Victim Dependent Variable: Length of Sentence

Types of Measures / Variables • Nominal / categorical – Gender, major, blood type, eye color • Ordinal – Rank-order of favorite films; Likert scales? • Interval / scale – Time, money, age, GPA

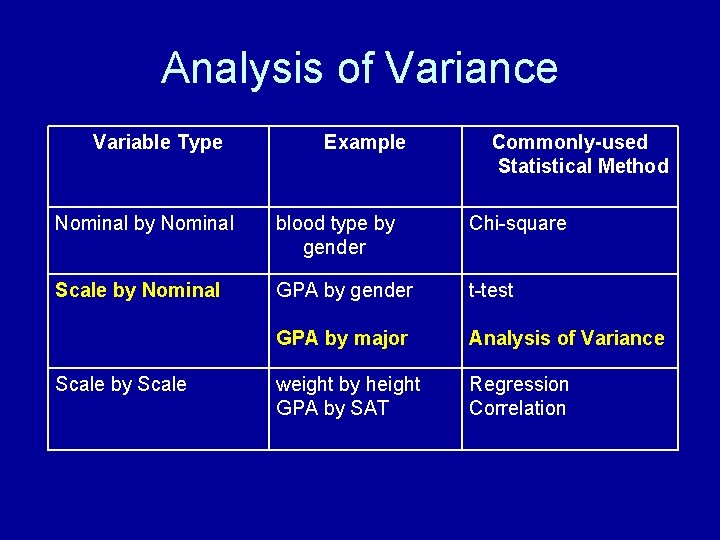
Main Analysis Techniques Variable Type Example Commonly-used Statistical Method Nominal by Nominal blood type by gender Chi-square Scale by Nominal GPA by gender t-test GPA by major Analysis of Variance weight by height GPA by SAT Regression Correlation Scale by Scale

Main Analysis Techniques Variable Type Example Commonly-used Statistical Method Nominal by Nominal blood type by gender Chi-square Scale by Nominal GPA by gender t-test GPA by major Analysis of Variance weight by height GPA by SAT Regression Correlation Scale by Scale

Stat Analysis / Hypothesis Testing 1. Form of the relationship 2. Statistical significance

Variables: Scale by Categorical • Form of the relationship: Means of each category (M & F victim) • Statistical Significance: Independent samples t-test

Means observed in Sample Victim Gender Average Sentence Male 6 months Female 16 months

Statistical Signficance • Q: Is this a “statistically significant” difference? • Can the “null hypothesis” be rejected? Null hypothesis: there are NO differences in sentencing for male vs. female victims

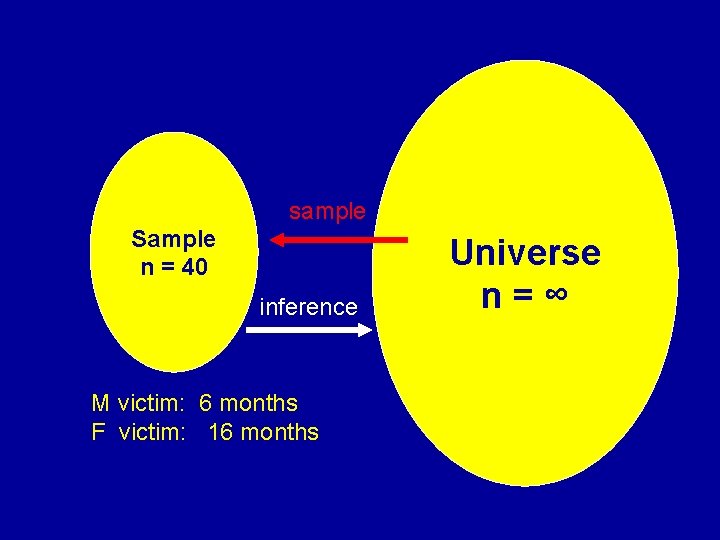
sample Sample n = 40 inference M victim: 6 months F victim: 16 months Universe n=∞

Logic of Statistical Inference • What is the probability of drawing the observed sample (M = 6 months vs. F = 16 months) from a universe with no differences? • If probability very low, then differences in sample likely reflect differences in universe • Then null hypothesis can be rejected; difference in sample is statistically significant

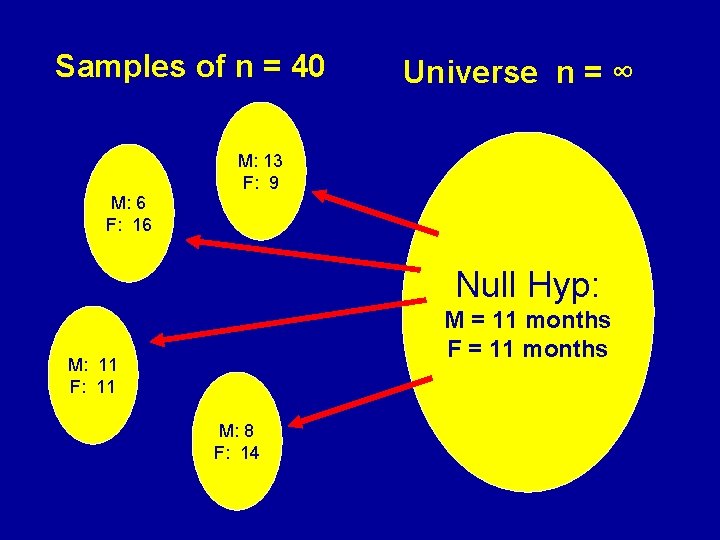
Strategy • Draw an infinite number of samples of n = 40, and graph the distribution of their male victim / female victim differences

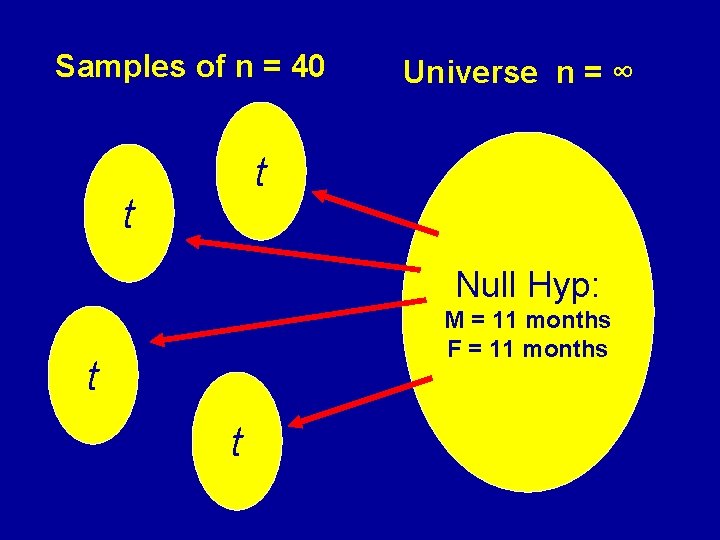
Samples of n = 40 Universe n = ∞ M: 13 F: 9 M: 6 F: 16 Null Hyp: M = 11 months F = 11 months M: 11 F: 11 M: 8 F: 14

T-test Sampling distribution: Mean difference Function of: 1) difference in means 2) variance (dispersion around mean)

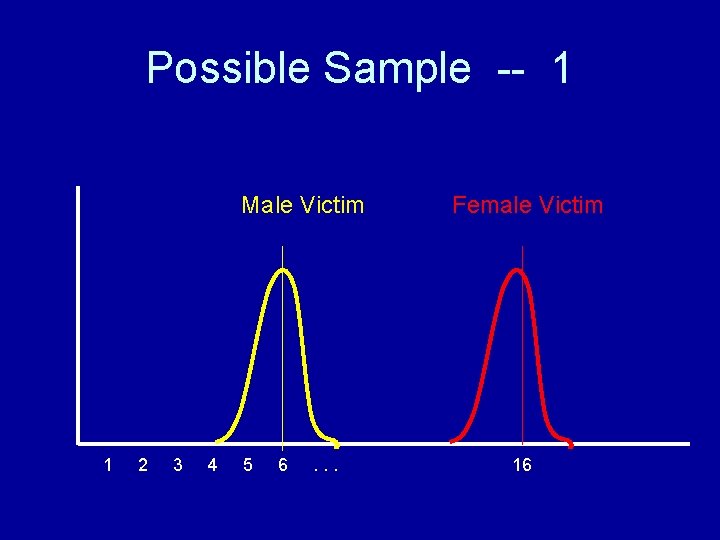
Possible Sample -- 1 Male Victim 1 2 3 4 5 6 . . . Female Victim 16

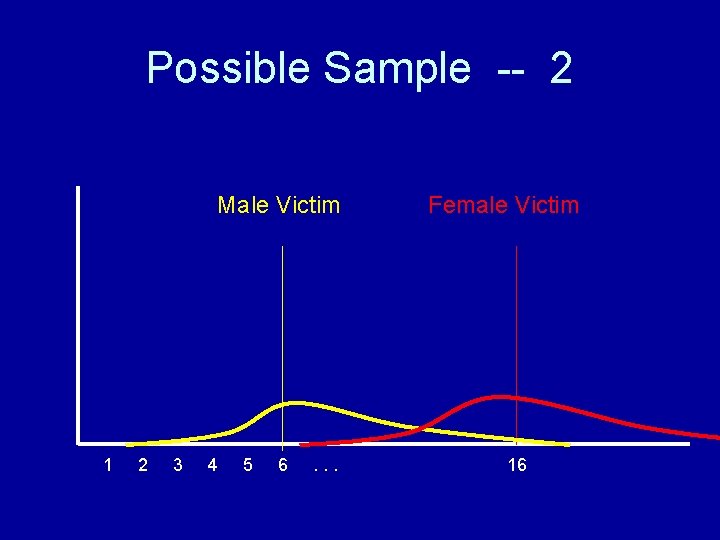
Possible Sample -- 2 Male Victim 1 2 3 4 5 6 . . . Female Victim 16

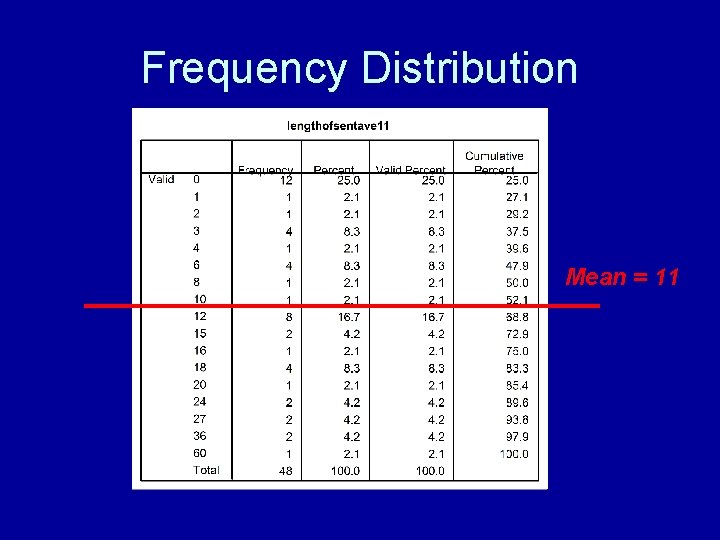
Frequency Distribution Mean = 11

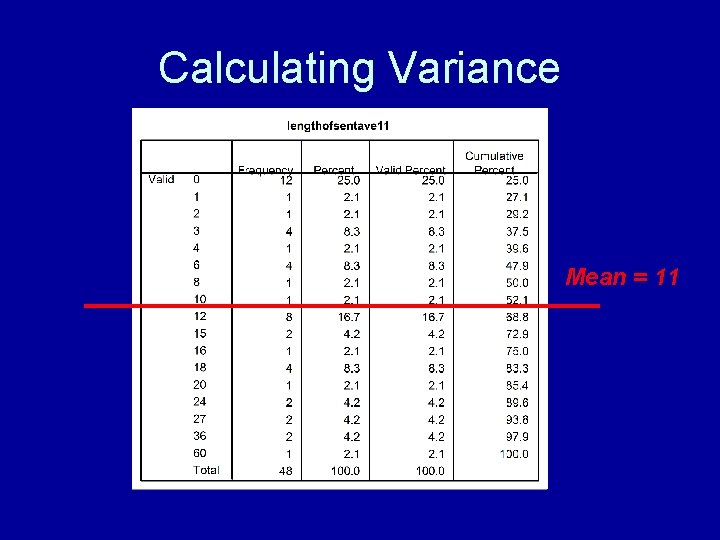
Variance = s 2 = but: x i - Mean )2 -----------N s 2 = x i - Mean )2 -----------N-1 Standard Deviation = s = variance

Calculating Variance Mean = 11

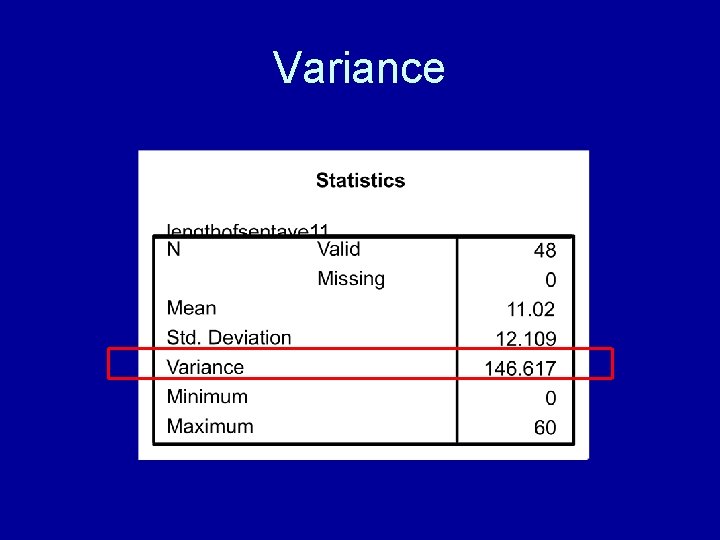
Variance

t distribution • Sampling distribution of a difference in means • Function of mean difference & “pooled” variance (of both samples) t = mean 1 – mean 2 ----------------sp√ (1/n 1) + (1/n 2)

Samples of n = 40 Universe n = ∞ mean dif & var Null Hyp: M = 11 months F = 11 months mean dif & var

Samples of n = 40 Universe n = ∞ t t Null Hyp: M = 11 months F = 11 months t t

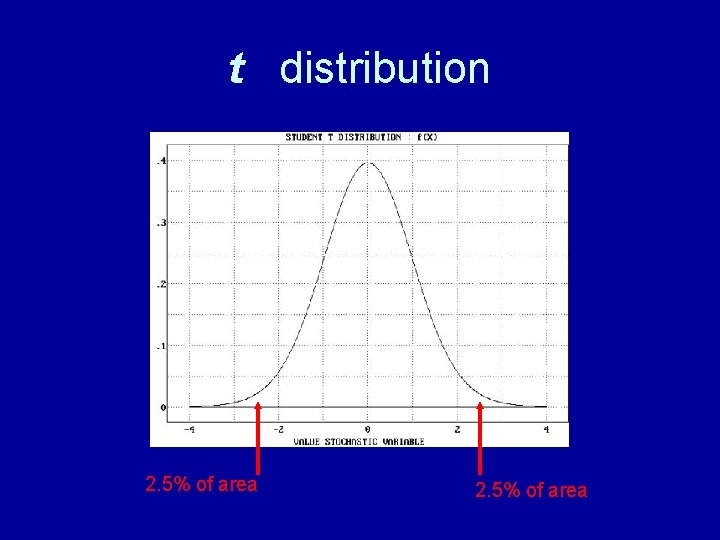
t distribution 2. 5% of area

Statistical Significance • If probability is less than 5 in 100, the null hypothesis can be rejected, and it can be concluded that the difference also exists in the universe. p <. 05 • The finding from the sample is statistically significant

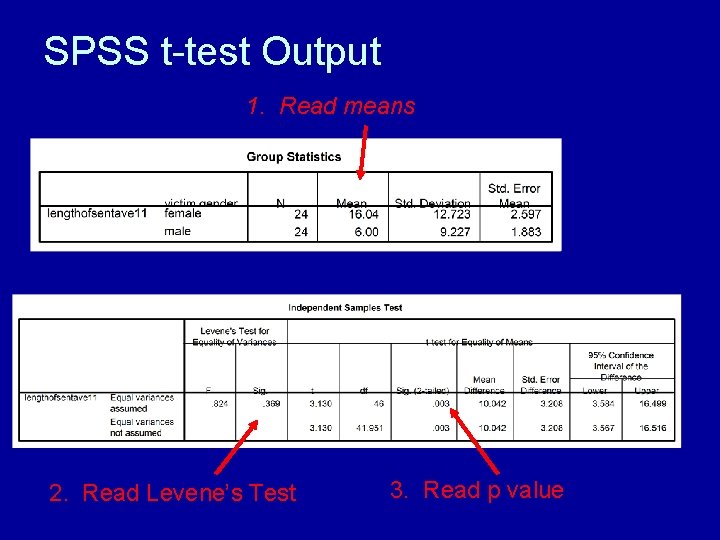
SPSS t-test Output 1. Read means 2. Read Levene’s Test 3. Read p value

Report Findings • “Assailants were given an average sentence of 16 months when the victims were female, compared to 6 months when the victims were male (df = 46, t = 3. 13, p. <. 005). ” • “Respondents gave longer sentences when the victims were female (16 months) than when they were male (6 months), a difference that was statistically signficant (df = 46, t = 3. 13, p. <. 005). ”

Statistical Analyses analysis of variance ( ANOVA ) Psych 250 Winter, 2011

Analysis of Variance Variable Type Example Commonly-used Statistical Method Nominal by Nominal blood type by gender Chi-square Scale by Nominal GPA by gender t-test GPA by major Analysis of Variance weight by height GPA by SAT Regression Correlation Scale by Scale

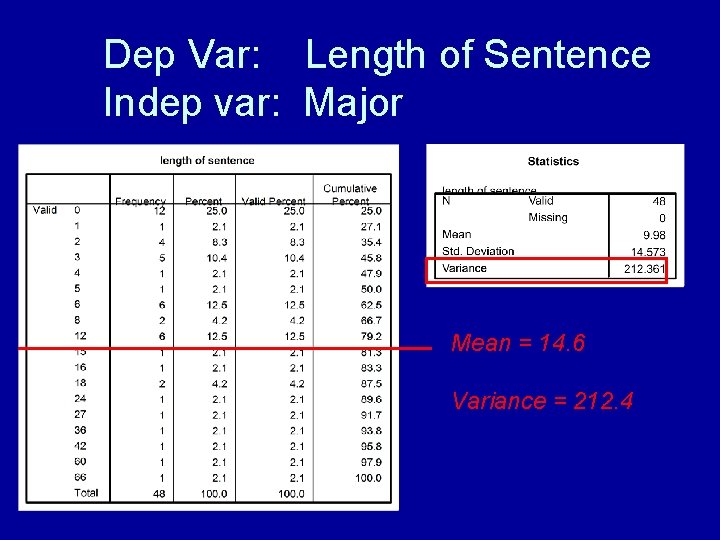
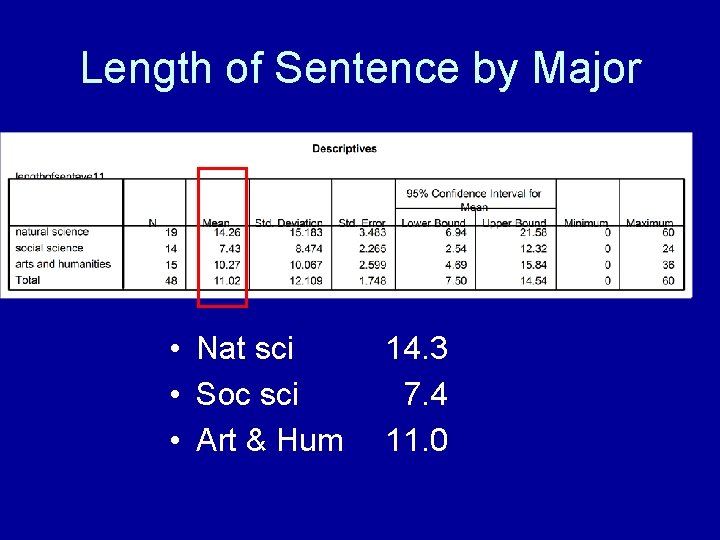
Dep Var: Length of Sentence Indep var: Major Mean = 14. 6 Variance = 212. 4

Form of Relationship (differences seen in sample)

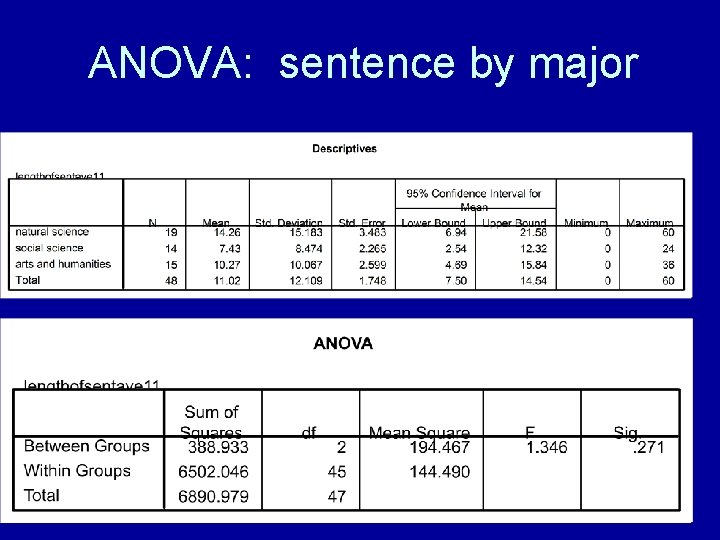
Length of Sentence by Major • Nat sci • Soc sci • Art & Hum 14. 3 7. 4 11. 0

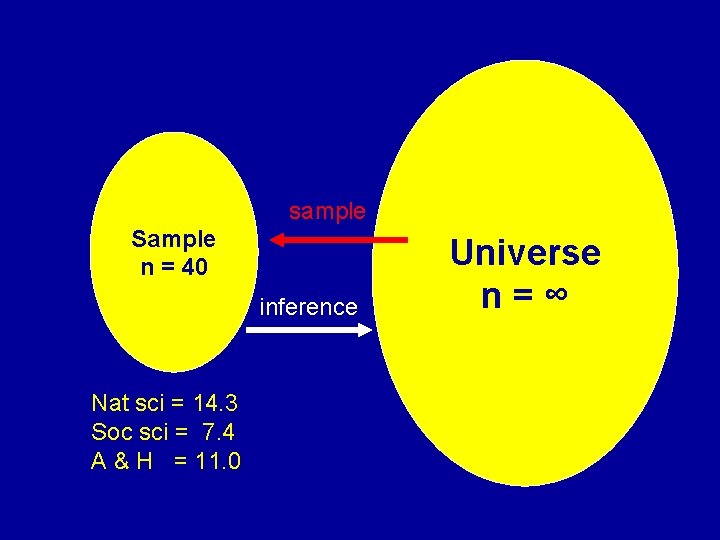
Statistical Inference ( generalize from sample to universe? )

sample Sample n = 40 inference Nat sci = 14. 3 Soc sci = 7. 4 A & H = 11. 0 Universe n=∞

Possible Sample -- 1 Social Science 1 2 3 4 5 6 7 8 Art & Human Natural Science 9 10 11 12 13 14 15

Possible Sample -- 2 Social Science 1 2 3 4 5 6 7 8 Art & Human Natural Science 9 10 11 12 13 14 15

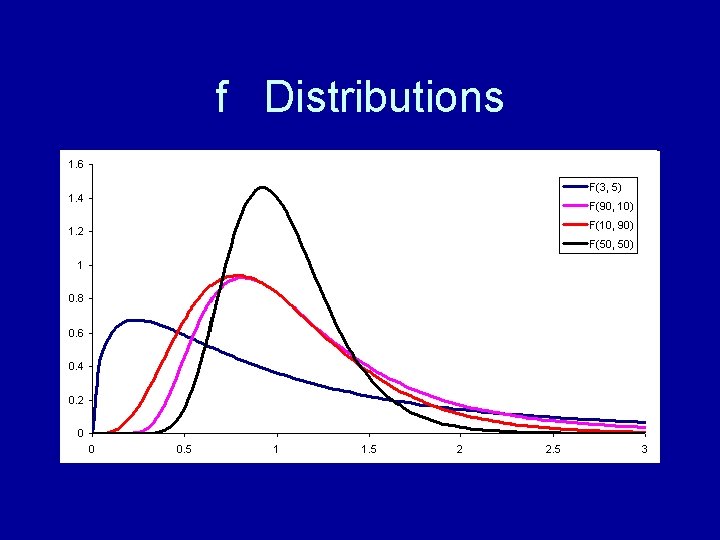
ANOVA Logic 1. Calculate ratio of “between-groups” variance to “within-groups” variance 2. Estimate the sampling distribution of that ratio: F distribution 3. If the probability that the ratio in sample could come from universe with no differences in group means is <. 05, can reject null hypothesis and infer that mean differences exist in universe

ANOVA Logic • Between groups: nsocsci(Meansocsci - Mean)2 + narthum(Meanarthum - Mean)2 +nnatsci(Meannatsci – Mean)2 / df • Within groups: (ni – Meansocsci) 2 + (ni - Meanarthum)2 + (ni - Meannatsci) 2 / df

F ratio between groups mean squares F = within groups mean squares

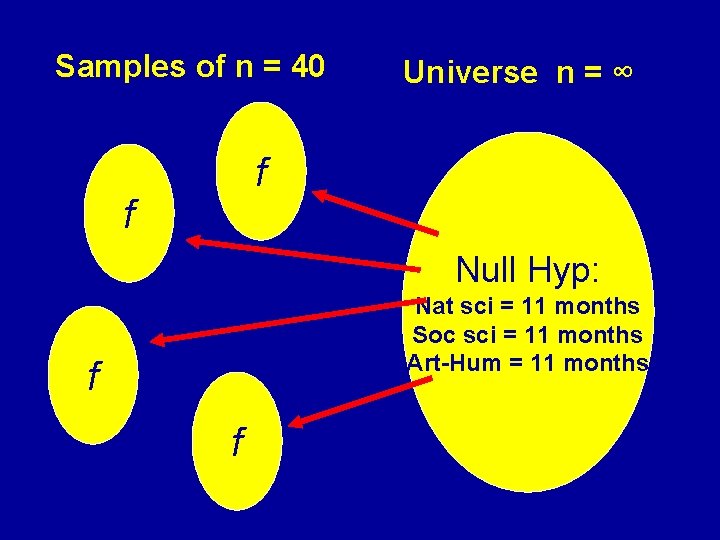
Samples of n = 40 Universe n = ∞ f f Null Hyp: Nat sci = 11 months Soc sci = 11 months Art-Hum = 11 months f f

f Distributions

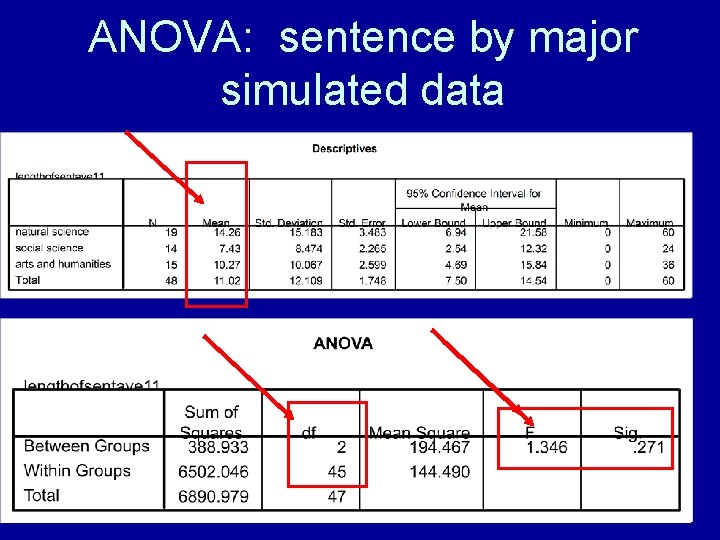
ANOVA: sentence by major

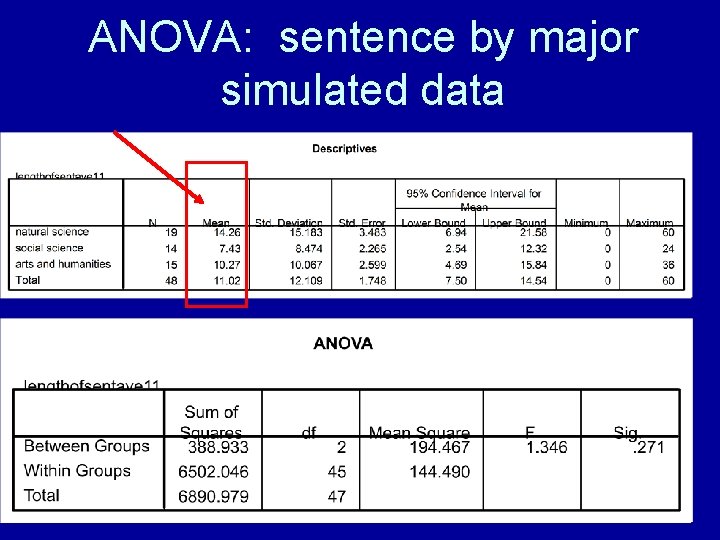
ANOVA: sentence by major simulated data

ANOVA: sentence by major simulated data

Write Findings “Social science majors assigned sentences averaging 7. 4 years, arts and humanities students 10. 3 years, and natural science students 14. 3 years, but these differences were not statistically significant (df = 2, 42, F = 1. 35, p <. 30). ”