Static Interconnection Networks CEG 4131 Computer Architecture III

Static Interconnection Networks CEG 4131 Computer Architecture III Miodrag Bolic 1

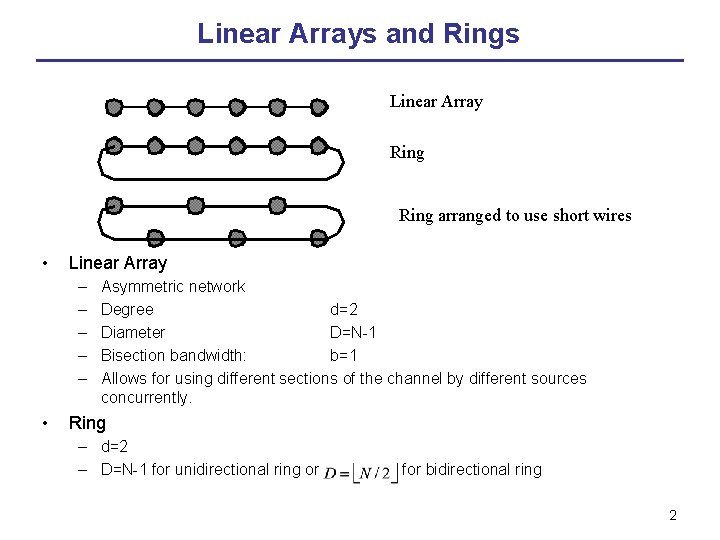
Linear Arrays and Rings Linear Array Ring arranged to use short wires • Linear Array – – – • Asymmetric network Degree d=2 Diameter D=N-1 Bisection bandwidth: b=1 Allows for using different sections of the channel by different sources concurrently. Ring – d=2 – D=N-1 for unidirectional ring or for bidirectional ring 2

Ring • Fully Connected Topology – Needs N(N-1)/2 links to connect N processor nodes. – Example • N=16 -> 136 connections. • N=1, 024 -> 524, 288 connections – D=1 – d=N-1 • Chordal ring – Example • N=16, d=3 -> D=5 3

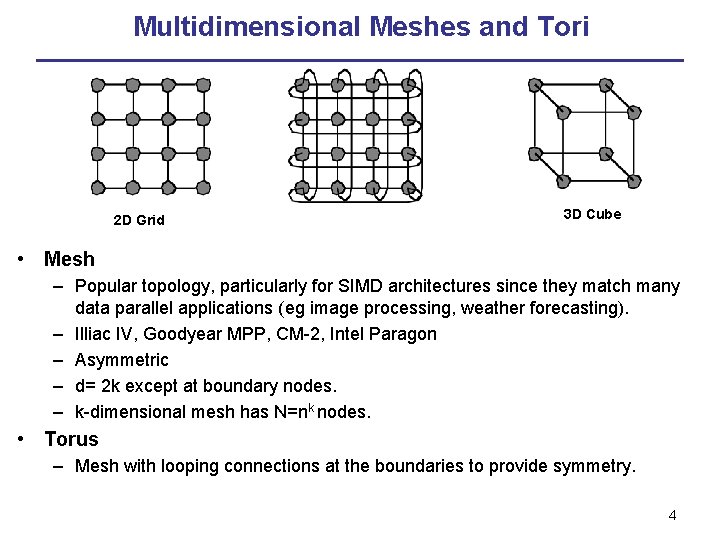
Multidimensional Meshes and Tori 2 D Grid 3 D Cube • Mesh – Popular topology, particularly for SIMD architectures since they match many data parallel applications (eg image processing, weather forecasting). – Illiac IV, Goodyear MPP, CM-2, Intel Paragon – Asymmetric – d= 2 k except at boundary nodes. – k-dimensional mesh has N=nk nodes. • Torus – Mesh with looping connections at the boundaries to provide symmetry. 4

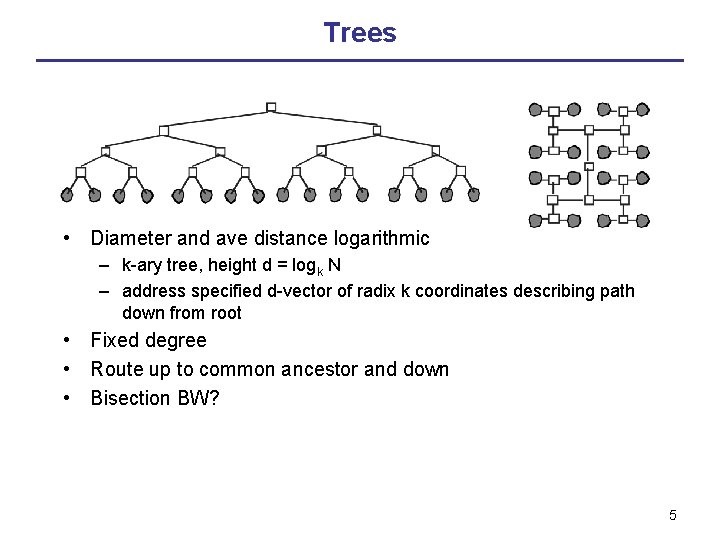
Trees • Diameter and ave distance logarithmic – k-ary tree, height d = logk N – address specified d-vector of radix k coordinates describing path down from root • Fixed degree • Route up to common ancestor and down • Bisection BW? 5

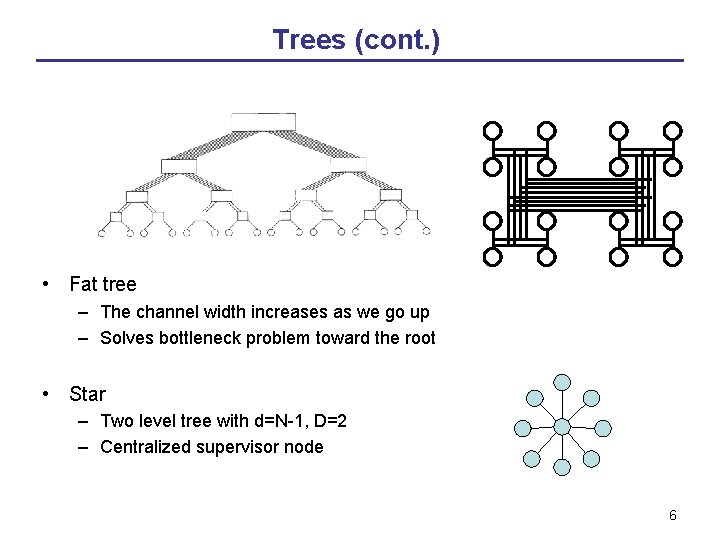
Trees (cont. ) • Fat tree – The channel width increases as we go up – Solves bottleneck problem toward the root • Star – Two level tree with d=N-1, D=2 – Centralized supervisor node 6

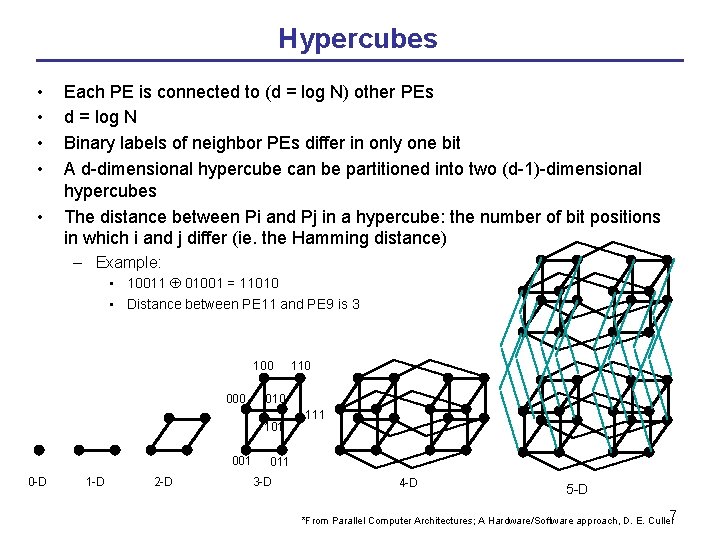
Hypercubes • • • Each PE is connected to (d = log N) other PEs d = log N Binary labels of neighbor PEs differ in only one bit A d-dimensional hypercube can be partitioned into two (d-1)-dimensional hypercubes The distance between Pi and Pj in a hypercube: the number of bit positions in which i and j differ (ie. the Hamming distance) – Example: • 10011 01001 = 11010 • Distance between PE 11 and PE 9 is 3 100 010 101 0 -D 1 -D 2 -D 110 111 011 3 -D 4 -D 5 -D 7 *From Parallel Computer Architectures; A Hardware/Software approach, D. E. Culler

Hypercube routing functions • Example Consider 4 D hypercube (n=4) Source address s = 0110 and destination address d = 1101 Direction bits r = 0110 1101 = 1011 1. Route from 0110 to 0111 because r = 1011 2. Route from 0111 to 0101 because r = 1011 3. Skip dimension 3 because r = 1011 4. Route from 0101 to 1101 because r = 1011 8

k-ary n-cubes • Rings, meshes, torii and hypercubes are special cases of a general topology called a k-ary n-cube • Has n dimensions with k nodes along each dimension – An n processor ring is a n-ary 1 -cube – An nxn mesh is a n-ary 2 -cube (without end-around connections) – An n-dimensional hypercube is a 2 -ary n-cube • N=kn • Routing distance is minimized for topologies with higher dimension • Cost is lowest for lower dimension. Scalability is also greatest and VLSI layout is easiest. 9

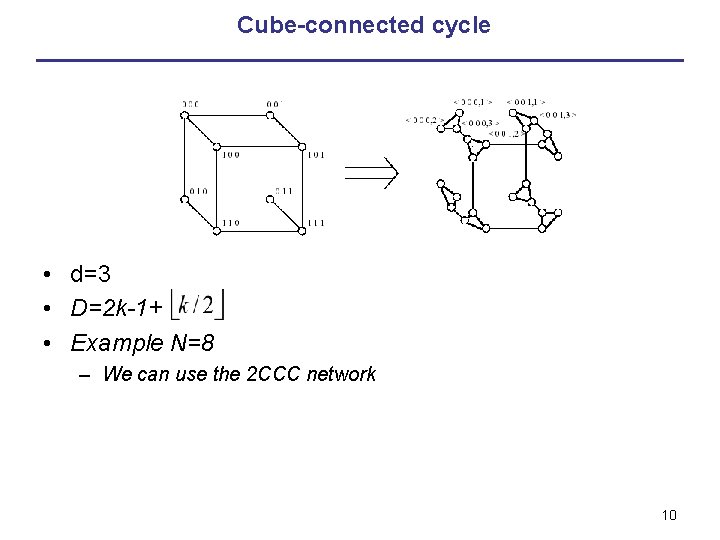
Cube-connected cycle • d=3 • D=2 k-1+ • Example N=8 – We can use the 2 CCC network 10

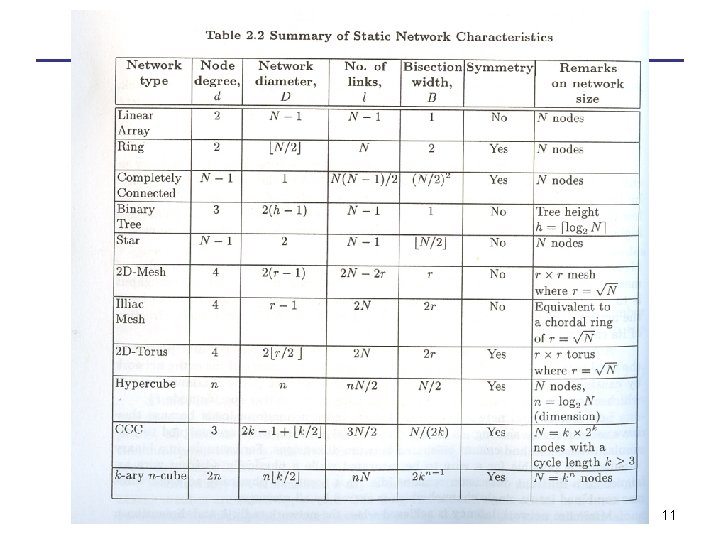
11

References 1. Advanced Computer Architecture and Parallel Processing, by Hesham El-Rewini and Mostafa Abd-El. Barr, John Wiley and Sons, 2005. 2. Advanced Computer Architecture Parallelism, Scalability, Programmability, by K. Hwang, Mc. Graw-Hill 1993. 12